LA NEF IIb - La chambre du roi

 

 

 

LA NEF IIb - La chambre du roi

 

 

 

 

 

 

La volonté de transmettre

 

Aux yeux de l'observateur moderne, la pyramide de Khéops est sans doute l'exemple le plus impressionnant de la volonté de transmettre des civilisations anciennes, cette volonté s'attachant avec la même au force au contenant - un édifice conçu pour franchir des millénaires – qu'au contenu -un ensemble d'idées géométriques rendues bien lisibles par les mesures et les proportions « rondes » et « explicites » de l'édifice.

Dans la logique de cette volonté, la première exigence était une condition de la seconde : pour que les idées géométriques puissent se conserver sans altération, il fallait que la structure de l'édifice le permette. La première chose à remarquer est que l'entreprise égyptienne est à cet égard un succès total, puisque, s'il existe d'innombrables débats touchant la « fonction » ou la signification même de la pyramide, en revanche, les dimensions en coudées égyptiennes de la pyramide et de la chambre du roi (pour nous limiter à ces deux données essentielles) font l'objet d'un accord unanime des égyptologues, académiques ou non.

Malgré cette réussite de principe de l'entreprise égyptienne, convenons que les pyramides laissent subsister à peu près entières, dans la compréhension des modernes, les deux énigmes initiales du « comment » et du « quoi ».

La première de ces énigmes concerne le niveau extraordinaire, mais mal connu, d'expertise technique, et de génie mécanique, requis pour la construction de tels édifices.

La seconde concerne la signification profonde de cette idéologie géométrique, dont les proportions de la pyramide se veulent explicitement les supports.

C'est évidemment à cette seconde énigme que se dédiera notre étude.

 

 

 

Le paradigme de Khéops

 

 

Comme le pied, la coudée est un étalon de mesure naturel, dont chacun dispose dans son corps.

Il existe, dans le monde égyptien, des définitions variables de la coudée, qui en vertu de la nature ne s'éloignent jamais grandement du demi-mètre. Les musées conservent quelques exemples d'une « coudée royale » mesurant approximativement 52 centimètres.

La pyramide de Khéops peut être qualifiée de témoin « paradigmatique », en ce que la mesure empirique de son tout aussi bien que celle de ses parties donne un résultat « aussi satisfaisant que possible » si l'on suppose que ses concepteurs ont utilisé une coudée royale de 52, 36 centimètres, précisément.

Sur ce postulat, on obtient pour la pyramide et la chambre du roi les mesures en coudées égyptiennes qui sont les suivantes :

 

Hauteur/Côté pyramide = 280/440 coudées royales de 52, 36 cm

Plancher chambre du roi = 10x20 coudées royales de 52,36 cm

 

Au sein de ce postulat le macrocosme (la pyramide) et le microcosme (la chambre du roi), se confirment et se soutiennent l'un l'autre de façon très convaincante. La chambre du roi est un volume de pierre en état de conservation parfait, dont les surfaces intérieures ont une précision comparable à celle qu'on pourrait aujourd'hui obtenir, avec l'aide d'un rayon laser ; de ce fait, même si les mesures empiriques du macrocosme – de la pyramide – ont pu être rendues précaires par l'érosion, cela n'a pas suffi à ce qu'un doute puisse survenir sur ce rapport 280/440, qui, en soi, s'impose comme un ratio porteur de « logos », comme une idée mathématique, grosse d'applications tant géométriques qu'arithmétiques.

L'acceptation de ce paradigme (qui, rappelons-le, fait l'objet à ce jour d'un consensus universel), est la seule « condition de foi » à laquelle soit soumise la prétention de faire dire quelque chose à l'architecture de la pyramide de Khéops. Car cette condition, en rapportant les grandeurs mesurables de la pyramide à des nombres, et donc à des unités, suffit pour « réduire », ou reconduire, le plan de la pyramide à une construction géométrique, avec toute l'exactitude conceptuelle que cela suppose.

Une fois délimité le consensus savant sur lequel s'appuie et auquel s'accorde notre étude, nous toucherons un mot, pour nous en débarrasser, des idées auxquelles elle ne s'accorde pas.

 

 

 

Une coïncidence malheureuse

 

Le rapport de la coudée royale égyptienne (ayant servi à l'architecte de Khéops) à notre mètre est de 0,5236

Ce nombre se rapporte, par une parfaite coïncidence, à la valeur arithmétique du rapport doré, et cela par le biais du triangle aurigène, puisque, si l'on additionne les côtés de ce triangle on obtient un nombre irrationnel qui est :

 

1+2+ 2,23606797 = 5,23606797

 

Dans une seconde phase d'étonnement, on peut remarquer que ce nombre de 0,5236 qui est le dixième du périmètre du triangle aurigène, se trouve, à l'égard de π, dans le rapport approximatif assez acceptable de 1/6 puisque

0,5236 x 6 = 3,1416

On aboutit à cette équation, qui est la juxtaposition de 2 coïncidences :

coudée/mètre = (1+2+rac5)/10

= (3 + Φ + 1/Φ)/10

= π/6

Equation dans laquelle le rapport de la coudée au mètre semble renvoyer de façon singulièrement chanceuse, aux nombres Φ et π.

Il convient de distinguer les deux parties dont se compose cette « constatation ». La seconde partie, qui revient à établir un rapport proportionnel entre Φ et π, rapport approximatif, et médié par le triangle aurigène, peut être considérée comme intéressante sur le plan des idées mathématiques, dans la mesure où ces nombres remarquables peuvent apparaître comme les opérateurs profonds d'une sorte de dialectique de la nature.

Dialectique, où le nombre π serait l'opérateur de ce qui est courbe, et le rapport doré, en tant rapport des rapports, ou rapport absolu, l'opérateur suprême de ce qui est droit. On peut en effet qualifier le rapport doré de « rapport le plus simple à soi-même » qui puisse s'exprimer dans la division d'un segment de droite.

On peut donc dire que le rapport de la coudée au mètre conduit par hasard à la considération d'un autre rapport, celui du nombre π au nombre Φ, qui peut sembler porteur d'une certaine consistance, d'un certain intérêt philosophique, d'ailleurs attesté et repérable dans la tradition pythagoricienne (comme nous le montrerons dans une autre étude).

Cette seconde partie de l'équation peut se simplifier par exemple par la formule approximative :

 

3 + Φ + 1/Φ = π x 6/10

 

En revanche, il convient de demeurer lucide sur la valeur de la « saisie initiale » sur laquelle s'appuie notre coïncidence , à savoir le rapport coudée/mètre, qui n'est, en soi, porteur de rien de plus que de l'idée totalement arbitraire de comparer ces deux étalons, séparés historiquement par des millénaires. Même si le rapport du mètre à la coudée avait été, (pour prendre une hypothèse encore plus frappante), directement égal au rapport π/Φ, et cela jusqu'à 15 chiffres après la virgule, il ne serait résulté, pour la compréhension des idées égyptiennes, rigoureusement rien d'intéressant d'une telle coincidence.

A la précision près, - mais la précision ne change rien à l'affaire - une telle coïncidence ne contiendrait aucune idée plus intéressante que, par exemple, la constatation que 10 francs = 1,6 euros, qui est une valeur proche du nombre d'or.

Dans le cas qui nous intéresse, tout ce qui est résulté d'une telle coïncidence, c'est l'occasion, pour beaucoup de gens, de s'en étonner, et ensuite, celle de supposer qu'il y avait derrière cette coïncidence un complot historique, dont la teneur est à peu près celle-ci : le mètre moderne est le plagiat inavoué d'un étalon de mesure universel qui aurait été connu de toutes les civilisations anciennes, étalon fondé sur une connaissance tantôt astronomique, (le méridien terrestre), tantôt micro-physique, (le diamètre de la goutte d'eau), mais toujours de style « moderne » : hypothèses aux allures légèrement paranoïaques, dont le tort principal aura été de détourner les esprits de réfléchir aux données mathématiques extraordinairement précises, et consensuelles, dont la pyramide est porteuse par ailleurs.

Au final, on aura abouti à ce décevant prodige, qu'un procès historique caractérisé par sa clarté, par la réussite de la volonté de transmission, se présente maintenant pour beaucoup sous les dehors de « l'opacité », et de l'occultation historique.

Il est donc grand temps de revenir à nos moutons.

 

 

 

Anatomie de la chambre du roi

 

 

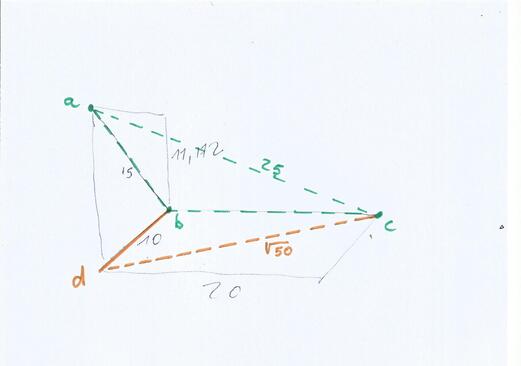
L'aire du plancher, comme celle du plafond, est un carré long de 10 x 20 coudées.

 Tout le monde s'accorde pour penser que la hauteur de la chambre, approximativement égale à 11,172 coudées, est choisie pour que la diagonale (ab) du petit mur vertical soit égale à 15 coudées.

  On remarque que le triangle (abc) est un triangle isiaque de côtés (15, 20, 25), tandis que le triangle (bcd) est un triangle aurigène de côtés (10, 20, racine50). Les deux triangles, vert et orange, sont les éléments d'une nef, mais cette nef diffère de la nef classique, du fait que les valeurs des côtés du triangle isiaque ont été multipliées par 5, tandis que celles du triangle aurigène ont été multipliées par 10.

  Du fait de ces opérations, la proportion entre les aires des triangles se trouve modifiée. Dans la nef classique, le rapport entre les aires des triangles aurigène/isiaque est de 1/6, tandis que, dans la chambre du roi, la proportion est de 2/3. Ces nefs appartiennent à différents types, qu'on pourra qualifier, pour le premier, de nef « solaire », et pour le second, de nef « de quinte ». Cette typologie n'est pas arbitraire, car si l'on examine, pour une nef quelconque, quels peuvent être les rapports d'aires entiers possibles, par exemple, au sein des 10 nombres de la décade, on s'aperçoit que seuls les rapports : 1/6, 6/1, 2/3 et 3/2 sont possibles. Autrement dit, en plus des deux exemples que nous connaissons déjà, seuls sont autorisés les rapports inverses de ces cas.

 

 

 

Prototype premier de la chambre du roi

 

La nef classique est un objet géométrique premier, d'une part, parce que le triplet isiaque 3-4-5 est le premier des triplets pythagoriciens, d'autre part, parce que les nombres 1 et 2 sont les plus petits entiers au moyen desquels on puisse construire un triangle aurigène.

  La nef égyptienne ne possède pas cette qualité de primarité, car il existe une solution de nef plus simple que celle de la chambre du roi, mathématiquement homologue, et qu'on appellera ici son prototype premier.

 

Dans ce prototype premier, les valeurs du triangle isiaques sont les valeurs premières (3, 4, 5), tandis que les valeurs du triangle aurigène sont doubles des valeurs classiques (2, 4, racine20). Ce prototype peut être qualifiée de nef de quinte première, du seul fait de la primarité du triplet (3, 4, 5). En effet, pour qu'un rapport de quinte soit possible entre un triangle aurigène et un triangle isiaque « quelconques », il faut d'abord qu'un triangle isiaque soit possible ; il n'existe donc pas de nef de quinte plus petite que ce prototype.

  On comprend bien que, si l'architecte de la pyramide n'a pas adopté pour patron ce prototype premier, c'est parce que les dimensions de la chambre, en coudées égyptiennes, auraient été bien trop exigües, et plutôt appropriées à la confection d'un coffre.

  Dans la suite de ce chapitre, nous aurons alternativement à nous référer soit à la nef originale de Khéops, soit à son protoptype premier, qu'il est donc important de bien distinguer.

 

 

 

Une propriété spéciale de la nef de quinte

 

  La nef de quinte possède une propriété unique, qui explique, très probablement, que l'architecte de Khéops l'ait choisie pour patron. Dans cette nef, en effet, le périmètre du triangle isiaque est égal à celui du carré long, formé de deux aurigènes jumeaux.

  Dans la chambre du roi, le périmètre du triangle isiaque, comme celui du carré long, est égal à 60 coudées.

  Tandis que, dans le prototype premier, les périmètres du triangle et du carré long valent 12.

  Nous avons déjà observé que, dans la tradition, le carré long et le triangle isiaque étaient identifiées l'un comme l'autre comme des figures matricielles de la géométrie sacrée, alors même que le triangle aurigène, lui-même, demeurait relativement inconnu. Et nous avons émis l'idée que ce manque de notoriété, ou de visibilité dans la tradition, pouvait se fonder aussi sur des raisons mathématiques.

  Dans la nef égyptienne, l'idéologie qui tend à mettre en exergue, à côté du triangle isiaque, le carré long formé de deux aurigènes jumeaux, trouve, précisément, la justification mathématique la plus immédiate, puisque la parenté des deux figures-symboles : le carré long et le triangle isiaque se traduit par une relation d'identité arithmétique : l'isopérimétrie.

  Et cette relation recèle encore quelque chose de plus profond.

  En effet, la relation d'isopérimétrie entre les deux figures a pour effet de les soumettre à un principe d'homologie, sinon d'identité ; par là, elle peut être comprise comme une relation de généricité, où l'une des figures est engendrée à partir d'une duplication (accompagnée d'une déformation) de l'autre.

 

rapport d'aire des triangles

2         /        3

 

  Ainsi, on peut imaginer que le carré long se soit formé à partir d'une duplirotation du triangle isiaque, mouvement qui aurait entraîné une déformation continue de la figure. Si l'on sait que, dans le contexte égyptien, l'usage de la corde à 13 nœuds était le b-a ba de la science de l'arpentage, on comprend que l'idée d'une telle transformation ait été naturelle à l'architecte de Khéops. Plus profondément encore, il est permis de voir dans cette transformation l'expression d'une « fonction isiaque », archétype d'une fonction d'arpentage sacré, caractéristique d'une famille de déesses architectes et bâtisseuses, telles que Mélusine.

  Dans la nef royale égyptienne, le rapport des aires des triangles est de 2/3 ; mais il est à noter que la quinte inverse, dans laquelle le triangle aurigène est plus gros que le triangle isiaque, possède des propriétés non moins intéressantes.

 En particulier, si l'on ajuste cette nef de quinte inverse au facteur 33 du triangle de Charpentier, on observe les propriétés suivantes.

 

rapport d'aire des triangles

3   /   2

 

  On se retrouve face à une nef de base 99, dont les segments entiers : 33, 44, 55, 66 ne sont autres que les valeurs du système k=11 de la cité isiaque, que nous avons rencontrées dans la première partie de cette étude.

 On observe d'abord ce rapport de commensurabilité généralisé entre les segments de la nef :

 

 3a = b+c = d+e =f²/e = 99

 

Mais on observe également une proportionnalité entre l'hypoténuse du triangle aurigène, égale à racine de (363 x 15) et les aires des triangles de la nef, respectivement égales à 363 x 3 et 363 x 2

 

 

 

Reprise de l'anatomie de la chambre : les trois rectangles et leurs prismes associés

 

Pour cette partie de l'exposé, nous utiliserons le prototype premier de la chambre du roi, qui se recommande par sa simplicité, et donc par sa généralité supérieure ; en sachant que, chaque fois que le lecteur voudra savoir à quels nombres correspondent, dans la chambre de Khéops, les valeurs du prototype premier, il lui suffira de multiplier ces valeurs par 5.

  Nous avons vu que la diagonale du petit mur vertical était le premier terme d'un triplet pythagoricien qui, dans la chambre de Khéops, est le triplet (15,20,25), et, dans notre prototype premier, le triplet (3, 4, 5).

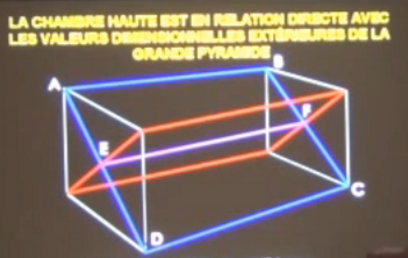
Notre chambre est donc divisée diagonalement, du sol au plafond, par un rectangle isiaque de côtés 3x 4 : le rectangle orange ABCD, qui divise la chambre en deux prismes triangulaires, les prismes ABCDIJ et ABCDLK

  Nous savons que le sol et le plafond de la chambre sont des carrés longs de côtés 2x4. Mais en raisonnant par analogie avec le rectangle isiaque, il nous est loisible de choisir, pour objet de référence de ce carré long, le rectangle vert EFGH qui divise la chambre en deux prismes rectangulaires égaux : les prismes EFGHABJI et EFGHLKCD

 Une remarque s'impose alors : il existe une troisième manière de diviser la chambre en deux prismes jumeaux, au moyen d'un plan rectangulaire. Ce moyen nous est fourni par le rectangle bleu IBKD de côtés (rac20 x rac5), qui divise la chambre en deux prismes, IBKDJC, et IBKDAL

 

 

Trois remarques

 

A.

  A la différence des deux précédents, ce rectangle a la propriété de paramétrer la hauteur de la chambre. Il apporte donc un éclaircissement mathématique immédiat à la hauteur approximative de 11,172 coudées égyptiennes que les égyptologues relèvent empiriquement dans la chambre du roi.

  En effet 11,172 / 5 = 2,2344

 à comparer avec :

 rac5 = 2,2360...

  A l'échelle de la chambre, le désaccord entre les deux valeurs est de l'ordre du millimètre. Il est donc raisonnable de supposer que la hauteur théorique de la chambre du roi, qui est en l'occurrence la valeur réelle qu'avait dans l'esprit l'architecte de Khéops, n'est pas 11,172 mais plus probablement 11,1803398875... = racine125

  Comme les valeurs du plancher aurigène et du plan diagonal isiaque, la hauteur de la chambre est une valeur simple qui, dans notre prototype premier, est la valeur racine 5, et dans la chambre de Khéops, la valeur racine 125.

 La valeur racine 5, comme on sait, peut être comprise comme un avatar de Φ ; c'est en tous cas de cette manière que Mattila Ghyka la traite dans son étude magistrale sur le nombre d'or.

 

 

B.

  Le rectangle bleu est un carré long puisque rac5/rac20 = ½

  La chambre du roi n'est pas l'harmonisation de deux rectangles, mais de trois, dont l'un est isiaque, tandis que les deux autres sont des carrés longs. Et il y a mieux, puisque les aires de ces trois rectangles s'harmonisent en une proportion continue :

  rectangle vert : 8

 rectangle bleu : 10

 rectangle orange : 12

 

  Dans la pyramide de Khéops, les aires des trois rectangles sont respectivement de 200, 250 et 300 coudées carrées. Pour passer du prototype à la chambre des égyptologues, il faut multiplier les valeurs par 5 x 5 = 25

  Soit :

  8 x 25 = 200 

10 x 25 = 250

 12 x 25 = 300

 

C.

  Nous rencontrons ici une redondance de l'idéologie qui, dans la tradition, tend à mettre en correspondance, à un objet isiaque, deux objets aurigènes.

  Et, au sein de cette trinité, la fonction de la hauteur de la chambre, et du rectangle bleu, (paramétrés par un avatar du nombre d'or) nous apparaît plus nettement aussi, comme une fonction d'intermédiation entre les principes hiérogamiques de la nef, représentés par les rectangles vert et orange, en rapport de quinte.

  Cette trinité de rectangles présente un air de famille avec le diagramme de Barazzetti, qui définit une réalité volumique en fonction de trois plans de coupe rectangulaires. Avec ces différences toutefois : que le diagramme de Barazzetti est fondé sur l'homologie des plans, là où notre triade articule une différence ; qu'il développe « principiellement » le principe d'orthogonalité, alors que ce principe est moins fondamental dans notre triade.

 

 

 

Du microcosme au macrocosme : la remarque de Grimault

 

Pour cette partie de l'exposé, nous quitterons temporairement le prototype premier de la chambre du roi, pour revenir au domaine des valeurs classiques de la pyramide, en coudées égyptiennes, - cela, dans le souci exclusif de ne pas rendre plus difficile la tâche du lecteur qui voudrait se reporter aux travaux de Grimault - en rappelant audit lecteur que, chaque fois qu'il voudra connaître la valeur des choses dans le prototype, il n'aura qu'à diviser les nombres par 5.

  Jacques Grimault remarque que, dans la chambre du roi :

 

 

rectangle (isiaque) ABCD  = 70 coudées = 1/4 de la hauteur de la pyramide (280)

  rectangle  ABFE = 55 coudées =  1/4 de la demi-base de la pyramide (220)

  Il nous reste à comprendre la signification de cette correspondance.

  En premier lieu, le macrocosme, la pyramide, est caractérisée par un ratio, qui est celui de la hauteur sur le côté – ou le demi-côté – de la base carrée de la pyramide, soit :

 280/440

 ou

 280/220

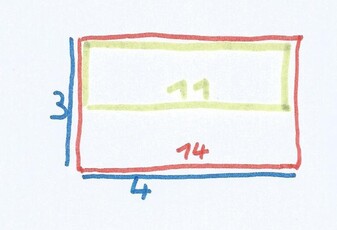
  mais ces valeurs ayant essentiellement fonction de ratios, il est évident qu'elles gagnent en intellectivité à être simplifiées, et sur cette base on admet que le ratio générateur d'une pyramide est le ratio 14/22 pour le rapport de la hauteur au côté de la base carrée, et 14/11 pour le rapport de la hauteur au demi côté de cette même base.

  Le ratio 14/11 (pour choisir l'expression la plus simple des deux) se présente donc à nous sous les apparences imposantes de ratio générateur de la pyramide de Khéops.

  Grimault remarque que le rapport 280/220 de la pyramide est formé des valeurs quadruples de celles du périmètre du rectangle isiaque de la chambre du roi (70), et du périmètre du rectangle qui est la moitié de ce rectangle isiaque (55). En divisant ces dernières valeurs par 5, on obtient celles du prototype premier

  70/5 = 14

 55/5 = 11

  En simplifiant le rapport 280/220 en 14/11, nous avons fait la même opération mathématique que celle qui consiste à convertir les valeur de la chambre du roi en celles du protoptype premier. Il n'est donc pas surprenant que nous retrouvions dans ce rapport 14/11, générateur de la pyramide, des valeurs qui sont, respectivement, celle du périmètre du rectangle isiaque, et celle du périmètre de sa moitié.

 

  On voit que, dans l'application de Grimault, la transposition du microcosme au macrocosme se fait uniquement par le biais du rectangle isiaque, du rectangle orange de la chambre du roi, les carrés longs vert et bleu ne jouant aucun rôle. Il convient donc de reconnaître à ce rectangle un caractère hégémonique sur la pyramide, qui s'explique suffisamment par le fait de sa primarité : à la différence du rectangle isiaque, les carrés longs bleu et vert ne sont ni l'un ni l'autre premiers, mais correspondent à des ajustements optimaux du « principe » du carré long aux valeurs premières du rectangle isiaque. Ce caractère hégémonique est donc conforme à la nature des choses.

  Nous en savons d'avantage, toutefois, sur la signification du ratio 11/14 qui commande à la fois les proportions de la pyramide, et celles de la chambre du roi. En effet, dans la géométrie du rectangle isiaque, ce ratio correspond au rapport du périmètre du rectangle à celui de sa moitié, concept auquel on peut attribuer toute la valeur d'un symbole marital où le polygone 11 serait l'Eve, le féminin, la moitié détachée du côté de l'Adam 14. Sous ce regard, le ratio 11/14 paraît donc lui-même chargé d'une signification hiérogamique.

 

 

Palindromes et doctrine « templière » du Temple

 

Les nombres 440 et 220 qui mesurent, respectivement, le côté et le demi-côté de la base carrée de la pyramide, sont des palindromes généralisés. Rappelons qu'un palindrome généralisé est un nombre qui est palindrome lorsqu'on l'ampute de ses zéros terminaux. Cette propriété est coextensive au fait qu'ils sont, l'un comme l'autre, des multiples du palindrome 11.

  Pour l'architecte égyptien, la « fonction palindrome », la fonction du 11, est donc celle qui est naturellement conforme à la dimension horizontale de la pyramide - le côté de sa base -, tandis que la « fonction 14 », la fonction « adamique », est celle qui est conforme à la dimension verticale de la pyramide - sa hauteur.

  Or, nous pouvons trouver un équivalent très exact de ces conceptions dans le dessin de la Jérusalem Céleste de l'église templière de Montsaunès.

 

Sur ce dessin, on remarque en effet que la hauteur du temple de la Jérusalem Céleste est indiquée par deux frises latérales de petits carrés, alternativement noir et blanc : 14 petits carrés.

 Aucune indication n'est donnée sur la dimension horizontale si l'on ne regarde que l'intérieur du dessin de la Jérusalem, mais en prêtant attention au dessin qui le surmonte, on s'aperçoit que cette grandeur est clairement indiquée : la longueur horizontale du rectangle de la Jérusalem correspond précisément aux onze douzièmes de celle du dessin du chrisme, qui le surplombe. Cette longueur horizontale est donc bien délimitée par 11 petits carrés – sans insister sur le fait que la totalité du dessin est gouvernée horizontalement par la symétrie du palindrome.

  Il nous reste à constater que l'architecte de Khéops et le peintre de Montsaunès, partageaient les mêmes conceptions sur les proportions idéales d'un temple. Mais aussi, que ces conceptions sont étonnamment en accord avec l'idéologie développée par Plutarque au sujet du triangle isiaque, idéologie qui attribue à Osiris la dimension verticale : - à cet égard la norme 14 commune à la pyramide et au temple de Montsaunès fera immanquablement penser aux 14 morceaux d'Osiris-lune - ; et à Isis, la dimension horizontale, qui est une dimension de déroulement et de développement, que sa nature propre assimile très naturellement à la fonction palindromique que nous rencontrons, aussi bien dans les valeurs horizontales de Montsaunès (11) que dans celles de la pyramide Khéops. (220)

 

 

microcosme/macrocosme : le rapport de l'être à sa moitié

 

Nous avons admis le principe que, dans la pyramide de Khéops, c'est le rectangle isiaque qui est le conducteur, ou l'hegemon, de la relation du microcosme-chambre au macrocosme-pyramide. Mais cette constatation ne nous empêche pas de nous demander à quoi peut ressembler « la relation du polygone à sa moitié » lorsqu'on l'applique, non plus au rectangle isiaque, mais au carré long.

  Et l'on observe ceci :

 

 

Appliqué au carré long, le schème qui associe le périmètre du rectangle à celui de sa moitié correspond au ratio 5/6 qui, dans la tradition, symbolise, précisément, le rapport du microcosme au macrocosme.

  Par généralisation, les deux ratios, 5/6 et 11/14 peuvent être compris comme des opérateurs symboliques de la plus haute généralité, exprimant l'un comme l'autre, sous des modalités différentes, le rapport du microcosme au macrocosme, ou celui de l' Adam primordial à sa moitié.

 

 

 

 

EPILOGUE : LA GRANDE TETRACTYS

 

 

Au terme de notre enquête égyptienne, nous avons observé que le ratio 11/14 qui fait le lien entre le microcosme-chambre et le macrocosme pyramide, correspondait, dans le rectangle isiaque, à la formule périmétrique d'hémi-partition de cette figure ; l'équivalent de ce ratio pour le carré long étant le rapport 5/6.

  Ces ratios ont assurément, relativement aux rectangles, un caractère profondément formel, en ce qu'ils "font dire" à ces figure quelque chose d'intime et précis concernant leur constitution interne ; et nous avons pensé pouvoir identifier dans ces ratios deux syzygies, deux couples primordiaux, dont le premier (5/6) représenterait le principe incitateur, ou animateur de la manifestation universelle, et le second (11/14), son principe récepteur, ou mondain.

 A présent, nous allons voir que ces deux ratios peuvent être considérés comme une redistribution de la grande tétractys 36, dont les deux jambes, quant à elles, sont constituées des pôles Impair et Pair.

 

 

GRANDE TETRACTYS                                                ENDOCOSME-EXOCOSME

 

 

  IMPAIRS                                 PAIRS

 

      1                                                     2                                                                         Eve     5

(endocosme)

     3                                                 4                                                                           Adam  6 

 

  5 ......liaison endocosmique .....6                                                                        Eve       11

(exocosme)

 7                                                      8                                                                        Adam 14

 

  (16)                 Totaux                     (20)

 

 

 Le total des impairs (16)  correspond à celui des Eve (5+11)

 Le total des pairs (20) correspond à celui des Adam (6+14)

 

 

Au sein de la grande tétractys, les valeurs du 3ème rang (5 et 6) forment l'endocosme aurigène, tandis que les valeurs des rangs 1, 2 et 4, sont des triplets qui additionnés, produisent l'exocosme isiaque (1+3+7) = 11 et (2+4+8) = 14                   

  La division catégorielle Impair-Pair de la grande tétractys se redistribue en principe "endocosmologique" (5-6) d'une part, et principe "exocosmologique" (11-14) d'autre part ; l'intéressant étant qu'en physique pythagoricienne, cette redistribution correspond exactement au concept timéen de mélange – ici mélange de Pair et d'Impair.

  On a vu dans la première partie de cette étude que ce rapport endo-exo s'illustrait de façon simple en terme de pavage, la spirale rythmant le chemin qui va de "l'état" (5/6) - le carré long central originaire, à l'état 11/14 - son "encadrement" isiaque.

Mais on pourrait également penser à une relation gnomonique, où comme il se doit, Isis "accueille" la graine aurigène.

 

 

 

Et, dans cette logique, il paraît évidemment intéressant de considérer le produit croisé de ces rapports :

(6/5) / (14/11) = 66/70 = 33/35

  Etonnamment, nos deux rectangles apparaissent ici comme deux jumeaux impairs, fort proches l'un de l'autre.

  Le rapport de ces ratios (6/5) et (14/11) se simplifie en 33/35, qui fait apparaître nos rectangles comme un couple gémellaire.  Ces mêmes ratios se résolvent exhaustivement (additivement) dans la tétractys 36

  Mais ce produit croisé 33/35 peut également faire apparaître le nombre 34, cher à Albrecht Dürer comme "membrane" ou interface de la nef, ce qui semble bien intéressant. On peut qualifier le 34 de gnomon de la structure nefique 33/35, en prenant le terme gnomon au sens "le plus nu" de vide séparateur.

 

  Et l'on se retrouve face à cette vision :

 

  Carré long                Nombre médiateur            Rectangle Isiaque            Nombre exhausteur

 

  33                                        34                                       35                                        36

 

  Situation dans laquelle on pourrait voir une résurgence de la formule des générations humaine et divine :

  3-4-5                   6

 

Le nombre 36 étant, comme chacun sait, le 8ème nombre triangulaire, à l'octave de la tétractys, cette fonction d'exhaustion aurait en outre pour effet colatéral de caractériser les valeurs des deux rectangles, 33 et 35, comme relatives, respectivement, à 3 et 2. Lorsque le triangle est rempli jusqu'au rang 3, on a 33, jusqu'au rang 2, on a 35.

 

 

 

(17 mars – 25 avril 2020)