La loi du gnomon

LE DEVELOPPEMENT CONTINU

 DE LA TETRACTYS

par Guillaume DENOM

 I.    LA LOI DU GNOMON

"L'ensemble des gnomons du carré, est égal à l'ensemble des gnomons du triangle équilatéral, est égal à l'ensemble des nombres entiers Impairs."

La loi du gnomon : G(c) = G(t.e) = I,  exposée, sur notre premier blog, dans les trois premiers articles de la deuxième section, est une loi importante de la mathématique. Son ancienneté, dans les termes où elle formulée ici, est attestée par divers témoignages, comme celui de Jean Philopon, selon qui les anciens appelaient "gnomons" les nombres impairs. S’il peut paraître étonnant qu'elle ne soit pas reconnue à sa juste valeur, et plus encore que, sous sa forme rigoureuse, elle semble même inconnue de la littérature mathématique contemporaine, il y a en réalité à cela des raisons précises et pour ainsi dire "naturelles".

La loi du gnomon est une loi synthétique, dont les applications se répartissent entre trois domaines de la mathématique : arithmétique, géométrie, logique. Pourtant, ce n’est pas une loi générale, c'est-à-dire qu’elle ne surplombe pas ces différents domaines à partir d’une position extérieure et dominante, mais, bien au contraire, elle agit à l’intérieur de chacun d’eux d’une manière spécifique.

La mathématique moderne n'est guère synthétique. Son geste le plus caractéristique est la généralisation, geste qui est bien différent de la synthèse, et en quelque manière opposé; puisque, si la synthèse est une action qui consiste à abstraire les propriétés intrinsèques que différents objets détiennent en commun, la généralisation consiste, elle, à partir d'une forme d'objet particulière (telle que la fraction, le nombre décimal, etc.), à définir une extension de cette forme ou formule particulière à l'ensemble du domaine d’objets dont elle dépend, par une action qui se qualifie elle-même de "conventionnelle". Par exemple : « tous les entiers peuvent être considérés comme des nombres décimaux »; ou encore : « les entiers peuvent être considérés comme des fractions. » 

En résumé, si la synthèse consiste en une connaissance sur des objets, la généralisation, elle, consiste en l'exploitation intensive d'une forme d'objet, - forme tenue en définitive pour l'"objet" le plus essentiel, alors même que, par sa nature, elle ne représente pour l'objet authentique dont elle est le moule ou la matrice - dans notre exemple : le nombre - qu'une possibilité de formulation parmi une indéfinité d'autres.

La généralisation, lorsqu'elle est pratiquée, comme elle l'est dans la mathématique moderne, de façon pour ainsi dire machinale, entraîne une double tendance de l'esprit mathématique, d'une part, à considérer comme "première", au sens de plus ontologique, la forme d'objet qui est la plus tard venue, ou la plus récemment définie, telle que le nombre réel ou le nombre complexe, d'autre part, à considérer qu'il n’existe pas de naturalité mathématique, mais que la mathématique est une façon de définir les choses qui est "conventionnelle" par essence, qui peut être "librement choisie".

Mais sans plus attendre, commençons par détailler les trois premiers domaines d’application de la loi du gnomon.

1. En arithmétique, la structure du gnomon est la triple articulation, intégralement coordonnée, du nombre impair (gnomon), du nombre entier (côté du polygone), et du nombre carré  (polygone gnomonique).

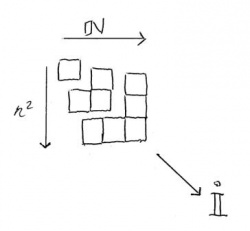
Dans cette structure, on a, sur l’axe horizontal, (ou plus généralement, sur le côté du polygone), la série indéfinie des nombres entiers ordinaux (1, 2, 3, 4, ...) ; sur la diagonale (ou, pour le triangle, la médiatrice verticale), la série des impairs cardinaux (1, 3, 5, 7, ...) ; enfin, sur l’axe des résolutions, la série des nombres carrés ordinaux : (1, 4, 9, 16,...) ; en précisant que, dans la logique du gnomon, on définit comme cardinaux les nombres qui possèdent une existence individuelle, en ce que chacun d'eux survit à la suppression de tous les autres membres, inférieurs et supérieurs, de la série à laquelle ils appartiennent, et ordinaux, les nombres qui ne subsistent qu'au sein d'une chaîne, ou d'un ensemble, dont chaque élément est une partie constitutive de son successeur. La structure arithmétique du gnomon est donc une application biunivoque qui, à chaque cardinal impair, associe une paire d'ordinaux, respectivement entier et carré  : I → (E, C), cette application permettant de représenter chaque objet gnomonique par un triplet de nombres. Si, par exemple, on assigne à l'impair la position médiane (par analogie avec la fonction qu'il exerce dans l'objet géométrique, où l'axe de symétrie directeur de la structure, qui est celui de la progression des gnomons impairs, est déterminé par son angle d'origine, dont il est la bissectrice), et à l'entier la position initiale, la série indéfinie des objets gnomoniques peut être formulée par une matrice (E, I, C), dont les premiers triplets sont : (1, 1, 1); (2, 3, 4); (3, 5, 9); (4, 7, 16); ... - ce système de coordonnées étant, rappelons-le, consistant et complet aussi bien pour le triangle que pour le carré gnomonique. ⁽¹⁾

2. En géométrie, le polygone gnomonique de rang 2, triangle ou carré, est la formulation minimale (ce qui implique : quantifiée) du principe géométrique qui est recouvert par les notions modernes d’endomorphisme et d’autosimilarité; et qui est, en langage courant, la propriété d'un objet, d'être constitué de parties semblables au tout qu'elles composent. 

polygones gnomoniques de rang 2

 3. La théorie du gnomon est la plus fondamentale des théories mathématiques contenant une application biunivoque des notions de nombre entier et de figure entière, et pour cette raison elle est l'interface la plus étroite qui puisse exister entre arithmétique et géométrie. Le gnomon est un objet mathématique dans lequel arithméticité et géométricité sont coproduits : car le gnomon est un nombre; le gnomon est le nombre de figures, que l'on doit ajouter à une figure, pour la reconstituer. En tant qu’interface la plus étroite possible entre nombre et figure, entre arithmétique et géométrie, le polygone gnomonique de rang 2, triangle ou carré, est le plus petit espace logique qui puisse exister : en précisant là encore, que l’on parle d’un espace quantifié, permettant une construction quantifiée de la logique, telle que la logique des tables de vérité. 

  4. C’est seulement dans un quatrième temps, après avoir détaillé la liste de ses applications dans chacun des domaines de la mathématique, que la loi du gnomon peut être envisagée synthétiquement, et que peut être évaluée sa place particulière dans l’appareil de la mathématique pythagoricienne.  La théorie du gnomon permet de donner un sens précis à la notion de tétractys : "clôture à quatre", ou si l’on préfère, "clôture quaternaire"; cette clotûre correspondant à la quantité d'espace nécessaire et suffisante pour que puisse se déployer la structure du gnomon, dans laquelle : graine + gnomon = 4.

La tétractys et le gnomon se déduisent en effet l'un de l'autre de la façon la plus simple, en ce que les étages de la structure triangulaire de la tétractys correspondent, biunivoquement, aux distances qui s'établissent entre les centres des blocs, au fur et à mesure que se remplit le gnomon du carré. Autrement dit, la même action qui, dans le gnomon du carré, se développe sous forme ordinale, est récapitulée, dans la tétractys, sous forme cardinale.

Sous cette armature logique, la notion de tétractys devient une notion mathématique utilisable, rendant possible une véritable mise en ordre des concepts mathématiques pythagoriciens. 

La notion de clôture est indispensable, en réalité, pour comprendre l'unité synthétique de ces différents concepts, et par suite, pour exposer de façon rigoureuse les applications contenues, sur notre premier blog, dans les trois premiers articles de la première section, à savoir : tétractys = base arithmétique (inclues dimensions décimale et négative) ;  tétractys = dimensions de l’espace et objets premiers de la géométrie ; tétractys = accords musicaux = noyau du système des médiétés, (en deux applications).

Par hypothèse, un traité, ou une théorie, de mathématique pythagoricienne, est un traité, ou une théorie, dont tous les axiomes sont déduits ou dérivés des propriétés mathématiques de la tétractys.

La mathématique pythagoricienne n'a a priori besoin d'aucune autre notion mathématique que celles qu'elle produit elle-même. Dans l'absolu, même les signes utilisés devraient être justifiés par la tétractys. Les chiffres arabes pourraient êtres remplacés par des tétractys à points triangulaires, les opérations logiques par les logons binaires, etc. En pratique, c'est évidemment difficile et un peu contre-productif, mais dans la visée qui est la sienne, la mathématique pythagoricienne n'utilise pas de signes « conventionnels », mais produit les signes dont elle a besoin.

Ceci n'est qu'un horizon, mais qui peut servir de guide. 

Au départ, la tétractys est une idée qui n'est pas définie, mais qui est montrée, qui est présentée dans la pensée. La mathématique pythagoricienne ne fait que répéter indéfiniment ce geste premier, ou plutôt le prolonger, le poursuivre par un développement continu.

La mathématique pythagoricienne est le développement continu d'une structure constante qui est la tétractys, dont la fonction est de déplier successivement, application par application, toutes les parties de la mathématique. Dans l’idéal, toutes les applications de la tétractys peuvent s'enchaîner par un mouvement continu, entièrement coordonné, au moyen d'un seul et unique opérateur topologique qui est le retroussement d'une structure : mouvement par lequel le dessous passe au dessus, et le dedans au dehors, par une poussée continuelle, et qui peut être illustré, de façon très intuitive, au moyen d'objets géométriques tels que l'hypercube. La question est complexe, mais, dans l'idéal, la présentation écrite de la mathématique pythagoricienne n'est pas la forme préférable. Une animation en 3D avec une voix off serait plus parlante, parce qu’elle permettrait d'avoir, au lieu d'images arrêtées, un mouvement réellement continu où l'on ne perdrait jamais de vue la structure ponctiforme à 10 points produite au départ. 

⁽¹⁾ Cette "triangularité" arithmétique semble apparenter  la structure du gnomon à d'autres structures arithmétiques connues, comme par exemple la célèbre formule de Ramanujan associant les nombres pi et e, dans laquelle on retrouve, sur l'axe horizontal, la série des impairs; sur l'axe vertical, la série des entiers; et du côté de la résolution, la racine carrée, opération inverse de l'opération "carré".        

                                                                                       Côté résolution : la racine carrée

 Axe horizontal : série des impairs (1, 3, 5, 7, …)          Axe vertical : série des entiers : (1, 2, 3, 4, ...)