Lambda de Platon et cubes gnomoniques de rangs 2 et 3

 

 

 

 

LAMBDA DE PLATON

et cubes gnomoniques de rangs 2 et 3

 

 

 

par G. Denom

 

 

 

 

 

Deux forces règnent sur l'univers : lumière et pesanteur.

Simone Weil

 

 

 

 

 

 

 

 

Le principe gnomonique de la musique pythagoricienne

 

 

Stephen Phillips a consacré, sur son blog, une étude géométrique intéressante au lambda platonicien (timéen pour d'autres), à voir ici, qui identifie dans cette structure l'interface arithmétique commune à la théorie musicale pythagoricienne et à ce qu'il nomme avec d'autres les "géométries sacrées"; même si nous devons confesser que cette expression n'a pas, pour nous, de signification bien évidente en pythagorisme, dans la mesure où, selon cette doctrine, c'est la géométrie elle-même qui peut être considérée comme "sacrée", ou, du moins, toute géométrie peut l'être, si elle est envisagée sous l'angle adéquat. Aussi, s'agissant de géométries issues des spéculations symboliques de différentes traditions ésotériques, telles que le yi king, l'arbre de vie ou le sri yantra, il nous semble suffisant de parler de géométries ésotériques, ou traditionnelles; avec l'avantage d'éviter ainsi, peut-être, le soupçon d'aller trop vite en besogne, et de présenter comme acquis, ou assuré, ce que l'on se propose en l'occurrence d'établir, ou d'illustrer.

 

La structure du lambda de Platon est morphologiquement analogue à celle de la dyade indéterminée, comme à celle du tenseur binaire radical de la linguistique guillaumienne. L'analogie ne se limite pas à une question de forme, puisque les deux jambes du lambda, constituées par le développement quaternaire, ou "tétractyque", en tant que rapporté à l'unité originaire, des carrés et des cubes des nombres 2 et 3, correspondent aux tensions "binaire" et "ternaire" du tenseur linguistique, à ceci près que, dans la topologie véritablement génétique de ce dernier, comme un peu partout dans la tradition pythagoricienne, la tension ternaire ou impaire, considérée comme fermante, (et correspondant à la catégorie du Même), précède la tension binaire ou paire, considérée comme ouvrante, (et correspondant à la catégorie de l'Autre) : ordre que l'on retrouve aussi bien dans la tension cosmologique empédocléenne, que dans la "table des opposés" d'Alcméon de Crotone.

 

 

                               

 

Point-atome : 1                                     Point-atome : 1

Arête-segment : 2                                Arête-segment : 3

Face : 4                                                 Face : 9

Volume : 8                                             Volume : 27

 

La musique pythagoricienne, comme on le voit, est construite avec de simples cubes. En effet, la jambe droite (ci-dessus) du lambda nous renvoie, exemplairement, aux valeurs du cube gnomonique de rang 3, comme le rubix-cube, dans lequel les nombres : 1, 3, 9 et 27 correspondent à l'atome-graine (point), à l'arête (segment), à la face (surface) et au volume du cube respectivement. Quant à la jambe gauche du lambda ci-dessus, elle n'évoque pas seulement les valeurs du cube gnomonique de rang 2 (où 1 = point-atome-graine, 2 = arête, 4 = face, 8 = volume), mais aussi bien certains processus sphériques, tels que celui de la division cellulaire, de la monade biologique.

 

 

 

Le cube gnomonique de rang 2 et la monade biologique

 

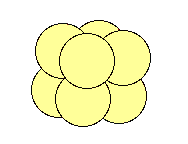
embryon au stade de 8 (x1) cellules, réparties en 2 hémisphères de 4 cellules

 

Il peut être intéressant de s'attarder un peu sur cette monade biologique, à ce stade de développement précoce où elle correspond au cube gnomonique de rang 2, car on constate qu'elle y est déjà dotée d'une structure tridimensionnelle, et que les principaux axes de symétrie de l'individu sont, eux aussi, déjà définis. 

Du point de vue monadologique, les trois axes de symétrie majeurs de la monade (l'un vertical, les deux autres horizontaux), correspondent aux "trous" ou aux interstices entre les cellules, mais aussi à l'historique de leurs mouvements relatifs; tandis que, d'un point de vue rétrospectif, ces trois mêmes axes fondamentaux déterminent l'emplacement des parois intérieures ou des surfaces de contact entre les cellules. Or, si la monade-point est déjà divisée en deux au stade du segment ou du "filament", elle se retrouvera, inévitablement, divisée en quatre au stade du plan ou de la "membrane" (disque), et en huit au stade de la cellule formée ou de la sphère (boule), puisque, du point de vue topologique, chacune de ces structures est formée ici par une duplication de celle qui la précède.

Le disque horizontal de la monade étant, structurellement, formé de deux segments entrecroisés, il est nécessaire qu'il corresponde à quatre points-éléments, et donc quatre "quartiers".

 

Mais d'autre part, le plan de l'horizon étant, par définition, décalé de 90 degrés par rapport au segment vertical de référence, et les deux segments composant la croix horizontale étant le lieu d'une intersection avec la dimension verticale, il est nécessaire que, dans cette dimension, il existe deux plans, deux disques identiques au disque de l'horizon, et perpendiculaires entre eux comme à ce dernier.

 

 

Dans la situation finale de l'orange biologique, il subsiste donc trois plans : un plan horizontal et deux plans verticaux, l'un frontal et l'autre sagittal, qui définissent huit (8) demi (1) - quartiers (4) répartis en deux hémisphères (2) de part et d'autre du plan horizontal de référence : - où nous retrouvons, dans leur expression naturelle, tous les nombres de la jambe gauche de notre lambda, structurellement identiques aux coordonnées intérieures d'un cube gnomonique de rang 2, comme dans la situation de ce personnage :

 

Chacun des trois plans générateurs étant divisé en quatre, on a au total 12 plans qui correspondent à l'ensemble des surfaces du cube gnomonique qui sont en contact avec une autre. La transformation du cube gnomonique de rang 2 en monade biologique sphéroïdale s'effectue simplement en remplaçant les trois carrés gnomoniques générateurs (CG de rang 2) par des cercles, ou plus exactement des disques.

 

Vision artistique de la monade biologique, à la structure formée de trois disques concentriques et perpendiculaires les uns aux autres, avec ses trois axes de référence.

 

En vertu des lois de la tension superficielle, les parois internes, aussi bien que l'enveloppe de la cellule, peuvent être recréés de manière très simple au moyen de trois anneaux assemblés sur les trois axes de la monade (composant un chrisme tridimensionnel), et de bulles de savon.

Pour une raison circonvoisine, (puisque l'octaèdre est la structure duale du cube), l'octaèdre - polyèdre à (8) x (1) faces - inscriptible dans la sphère, composé de deux pyramides (2) à base carrée (4) opposées, et dont les coordonnées des 6 sommets sont définies par les trois axes directeurs de la monade, est, du point de vue physique qui est celui de l'équilibre des vecteurs, la plus stable des structures spatiales issues de la théorie pythagoricienne des solides.

 

 

  

 

De fait, il est possible de construire un octaèdre évidé, ou réduit à l'état de squelette, au moyen de l'entrecroisement de trois carrés, dans lequel aucune des propriétés essentielles de ce solide n'est perdue; et ces trois carrés correspondent aux trois carrés gnomoniques de rang 2 qui définissaient, précédemment, les parois intérieures du cube gnomonique de rang 2, comme ils correspondent aux trois disques de la monade biologique.  Il est également possible de construire cette figure avec huit tétraèdres irréguliers dont les bases sont des triangles équilatéraux et les trois autres faces des triangles isocèles rectangles.

 

 

 

 

 

Tension binaire et tension ternaire : deux forces physiques très concrètes

 

 

Cette parenthèse refermée, on pourra résumer ce qui précède en disant que les deux jambes du lambda nous représentent les propriétés de développement gnomonique propres aux nombres monadiques 2 et 3, dans leur rapport conjoint à l'unité cardinale, et sous la définition spatiale quadridimensionnelle qui est spécifiquement la leur dans la mathématique pythagoricienne.

A présent, comment caractériser la différence entre les deux systèmes, - entre les deux jambes du lambda?

Dans un cube gnomonique de rang 2, le centre de symétrie n'est pas un élément du système.

Si la tension paire, la tension binaire, est considérée comme ouvrante ou centrifuge, c'est parce qu'elle a pour centre géométrique un vide séparateur. Dans l'ordre des interactions physiques, la tension binaire est donc associée à la force électromagnétique et, caractéristiquement, à la lumière, comme en général à tout phénomène de rayonnement; - force dans laquelle, à tous les étages d'observation, la bipolarisation semble être une propriété "immanente". Si la lumière est ce qu'il y a de plus rapide, c'est parce qu'elle est ce qui "fend" et divise le mieux l'espace. A une autre échelle, la tension binaire pourrait aussi être associée au phénomène de la fluctuation quantique, propriété essentielle du vide, productrice de paires de particules.

A l'inverse, dans un cube gnomonique de rang 3, le centre de symétrie est un élément du système, celui des 27 petits cubes qui est situé au centre de celui-ci, autour duquel un plus grand cube est construit de manière continue, à la manière d'un fruit autour de son noyau, (ce qui en fait une représentation achevée, car tridimensionnelle de la dyade indéterminée), et vers lequel convergent l'ensemble des segments ternaires particuliers dont est constitué le cube. Le véritable gnomon (tridimensionnel) du cube peut donc, à cet égard, être regardé comme un ensemble sphéroïdal d'une seule pièce, constitué de 26 éléments groupés autour d'un noyau. Si la tension impaire, la tension ternaire, est considérée comme centripète ou fermante, c'est parce qu'elle a en son centre un être positif, qui est en même temps un attracteur. Dans l'ordre des interactions physiques, la tension ternaire est donc associée à la force gravitationnelle, comme l'illustre exemplairement le problème à trois corps.

Si la tension ternaire précède logiquement la tension binaire, c'est parce qu'un être précède, logiquement, la possibilité qu'il a d'être coupé en deux; c'est parce que, pour que puisse être coupé en deux quelque chose, il faut qu'il y ait quelque chose. La tension ternaire a pour centre la monade cardinale, l'objet, tandis que la tension binaire a pour nature profonde la nature du couteau. Or c'est l'être qui tient le couteau, et non le couteau qui tient l'être.

Il n'y a sans doute pas d'autre force agissante dans la nature, que ces deux forces dont les effets sont connus et visibles à l'échelle humaine : celle qui fait choir une pomme à terre, et celle qui fait jaillir la lumière d'une lampe électrique. Dans la mesure où, selon le principe sain de la physique, une force se connaît à ses effets, les forces nucléaires faible et forte, dont les effets, annihilés à notre échelle, nous sont invisibles, puisqu'elles sont confinées dans le noyau de l'atome, où elles n'entrent en jeu que pour faire tenir ensemble des composants élémentaires qui, sans elles, ne s'accorderaient pas, n'ont assurément pas le même statut scientifique, et nous renseignent sans doute davantage sur les limites actuelles de nos théories, sur notre connaissance insuffisante de la délicate horlogerie selon laquelle les forces fondamentales peuvent se combiner à l'échelle subatomique, que sur la nature des choses. On peut déjà remarquer que les forces nucléaires "faible" et "forte" ne sont, par leurs noms mêmes, pas associées, comme les deux précédentes, à une multiplicité d'effets micro, méso et macroscopiques, mais à un topos bien défini qui est le noyau de l'atome, or il est singulier et scientifiquement inhabituel que les effets d'une force physique, et a fortiori d'une force universelle, soient assujettis et limités à un topos particulier; car le noyau de l'atome n'est qu'un lieu aussi déterminé de la nature que peut l'être la coquille d'un oeuf, et par conséquent lorsqu'on parle de forces nucléaires forte et faible on ne dit, scientifiquement, rien de plus impressionnant que "la petite et la grosse force de la coquille", qui sont précisément les deux dont vous avez besoin pour que votre coquille n'explose pas. Mieux vaudrait, peut-être, s'interroger sur ce que l'on a mis dans l'oeuf. Rien de commun, donc, avec des forces universelles dont les effets directs se diffusent réellement à de multiples niveaux d'observation de la nature, comme celles que nous évoquions au début de ce paragraphe, savoir : la gravitation et la force électromagnétique.

Si nous pensons que deux tensions sont suffisantes pour expliquer ce qui se passe dans le monde physique; c'est parce que nous avons  constaté que deux tensions étaient habituellement suffisantes, pour expliquer ce qui se passe dans le monde mathématique. On peut sans doute dire que si un problème ne relève pas de l'une de ces tensions, il ne relève pas de la mathématique; car nous ne parvenons pas à concevoir une forme de tension, opératoire en mathématique, et ayant donc un sens pour cette science, qui ne procède pas de l'un ou l'autre de ces archétypes, relevant des propriétés universelles de la dyade indéterminée, ou qui n'en dérive par composition. Or concernant maintenant les possibilités d'explication propres à la science physique, nous pensons qu'une explication physique ne sera jamais satisfaisante pour l'esprit, si elle ne s'achève pas dans une représentation du genre mathématique; cette affirmation qui pourrait presque apparaître comme un cliché ou une généralité creuse, ne l'est pas en réalité pour nous, puisqu'elle revient à rappeler la science aux sources pythagoriciennes de son inspiration première, au prix d'un petit effort pour enjamber cet autre cliché, selon lequel en pythagorisme "tout est nombre". La "mathématique pure", en tant que science des possibilités a priori de l'être, sera toujours légitime à s'exprimer en science physique, dans la mesure où la science physique elle-même ne se reconnait pas d'autre garant, n'admet pas d'autre genre de monstrations et de preuves, que celles que lui apporte la mathématique. Et ce, bien que depuis Galilée, cette mathématique pure en soit finalement venue à être regardée comme un instrument abstrait et froid, dont l'usage ne se justifie, au fond, qu'à raison de ses succès pratiques en terme de prédiction et de calcul.

 

 

Même - Autre, Un - Multiple

derrière ces catégories dialectiques : deux constantes cosmologiques

 

 

Ces forces physiques bien connues et manipulables à l'échelle humaine, sont aussi manifestes à une échelle supérieure; puisque c'est à elles que se résume l'activité apparente du ciel. 1. Les astres gravitent et 2. émettent des rayonnements, des ondes, au premier rang desquels la lumière. Si la lumière est ce qu'il y a de plus rapide, c'est parce qu'elle est l'être dont la tendance naturelle, le vecteur, est le plus opposé à celui de la gravitation; en tant que limite constante du système cosmologique, elle représente donc à cet égard un extremum, un correspondant polaire à la gravitation. Si la gravité est ce qui fait que toutes choses se dirigent du même côté (ou du côté du Même), la lumière est ce qui se rend le plus vite de l'"autre" côté, (ou du côté de l'Autre). Ce n'est pas sans raison que le nom de la tétractys désigne par le mot "rayon" ce qui est en fait une dimension mathématique, et pas seulement d'espace, mais d'espace-temps. Certes une réalité mathématique est nommée ainsi au moyen d'une analogie physique; mais l'important est qu'il s'agit en l'occurrence d'une analogie correcte.

A l'inverse, nous voyons avec les trous noirs que, lorsque la gravité d'un astre est excessive, les rayonnements de la lumière sont non seulement piégés et emprisonnés dans cet astre, mais littéralement aspirés dans une direction inverse de celle qui est naturellement la leur, qui est celle de la singularité et du point; de sorte que les vecteurs d'extension de la lumière qui étaient précédemment des vecteurs de division de l'espace macroscopique, doivent à présent être des vecteurs de division de l'espace microscopique, de la dimension du point, elle-même d'extension indéfinie. Et il est remarquable que la monade biologique puisse être considérée en même temps de ces deux manières : comme un problème de division d'une singularité primordiale, et comme un processus de croissance ou de développement de l'individu. Cela montre que la cellule vivante relève d'un accord ou d'un équilibre entre deux tendances essentiellement contraires.

*

Dans la tradition pythagoricienne, il est dit que le monde résulte d'un accord, d'une harmonie, ou d'un mélange, entre ces deux tensions contraires, appelées "même" et "autre", - qui ne sont pas seulement des agents logiques, comme on l'a généralement cru à tort, mais aussi des forces physiques très concrètes, l'une "rentrante" , l'autre "sortante", l'une aspirante ou "siphonnante", évoquant un entonnoir ou un vortex, l'autre émanante ou rayonnante. C'est dans la connaissance de cette harmonie, de cet accord intime de la nature, que consiste l'art pythagoricien de la musique des sphères, dont le Timée offre l'exemple le plus connu. Toutefois, si dans le domaine purement mathématique qui est celui de la théorie musicale, l'harmonisation de ces deux systèmes, binaire et ternaire, peut s'effectuer au moyen des trois seules médiétés classiques : arithmétique, géométrique et harmonique, qui forment du reste un tout logique, il n'en va pas de même dans le domaine des sciences de la nature, où une quatrième médiété entre en jeu : la médiété Nicomaque 10. Or, de ces deux plans ontologiques, le plan mathématique et musical, et le plan de la science physique, le second est plus développé et plus complet, puisqu'il inclut le premier comme partie, comme noyau mathématique, tout en le développant selon une modalité particulière d'existence, qui est celle, en l'occurrence, de notre univers physique. Entre les deux, il y a toute la différence qui existe entre la simplicité de la tétractys, et la richesse du monde physique, entre les conditions de possibilité de la forme, et la réalisation d'une forme particulière. Le problème du Timée de Platon est qu'il semble avoir tenté de réunir dans un récit continu, en fonction d'analogies trompeuses, des considérations qui, à l'origine, relevaient de plans ontologiques différents; de sorte que la seule façon d'en user avec ce texte semble être d'en considérer les morceaux isolément, comme les pièces d'un puzzle incomplet en l'état, comme on le fait d'ordinaire pour le reste de la tradition pythagoricienne. Ces réserves faites, il importe surtout de souligner que les tensions binaire et ternaire du lambda de Platon correspondent, de façon parfaitement évidente, aux deux tensions fondamentales de la cosmologie empédocléenne; ou encore, pour enfoncer ce clou, la dialectique du Même et de l'Autre ne présente aucune différence avec celle, empédocléenne, de l'Un et du Multiple, la seule différence consistant dans le choix d'un couple d'agents logiques dans le premier cas, et mathématiques dans l'autre; mais cette différence ne signifie en l'occurrence rien de plus, que le fait que la réalité elle-même puisse être envisagée de manière alternative sous ces deux aspects, sans cesser d'être une et la même; de sorte que, malgré le déni de la critique historique et philosophique à ce sujet, on est contraint d'admettre qu'il y a, entre ces deux monuments de l'ancienne physique pythagoricienne, un accord absolu sur les principes, comme il est naturel et inévitable dans toute tradition qui se respecte, même s'ils diffèrent dans la façon de les appliquer.

*

 

Du point de vue strictement physique, il n'existe sans doute que deux constantes véritablement universelles : la constante gravitationnelle et la vitesse de la lumière; toutefois un univers gouverné par ces deux seules constantes serait, selon toute vraisemblance, incapable de faire naître quelque chose, si une troisième constante n'intervenait dans le processus, celle-là d'essence mathématique : la constante phi, pour des raisons qui ne pourront ici qu'être effleurées.

Sur le plan ontologique particulier qui est celui de la Nature, toute existence individuelle repose, du point de vue topologique, sur une assise en forme de double spirale, l'une rentrante, l'autre sortante, spirales qui, en arrivant au contact l'une de l'autre à partir de vecteurs opposés, agissent l'une à l'égard de l'autre comme des freins, et forment donc une médiation entre deux tendances de la nature, l'une centripète, l'autre centrifuge, qui l'une comme l'autre, sans cette médiation conduiraient cette existence individuelle à disparaître physiquement. L'existence individuelle d'un être naturel est donc conditionnée à celle d'une "matrice" topologique, capable de freiner les forces universelles qui le traversent, en fonction d'un milieu qui est, pour cet être donné, celui de sa survie, de sa continuité dans le temps, mais qui est aussi une réelle position et une coordonnée mathématique, ou plus exactement un système à deux coordonnées, composé d'un centre et d'un environnement, (selon les deux sens que revêt en français le mot "milieu", compris ici synthétiquement); - freiner ces forces, sans toutefois les stopper complètement, sans quoi aucun mouvement, ni aucune existence individuelle ne serait possible.

 

 

Le problème topologique de la monade-univers, autrement appelée Nature. Le Mélange et l'Harmonie : le "frein à main" de la nature universelle.

 

Pour se donner une idée du problème, on peut se représenter, par exemple, l'action que les tensions binaire et ternaire exercent sur un objet comme le segment; en ayant à l'esprit le fait que le segment n'est qu'un état, et donc une représentation particulière de la monade, et qu'à cette réserve, les choses ne doivent pas se passer de manière très différente pour la monade-univers. La tension ternaire centripète détermine le segment à se contracter en direction d'un point qui est son centre, afin de continuer à ne former qu'un seul objet. La tension binaire centrifuge le détermine à se séparer en deux parties égales, dont chacune se précipite dans une direction opposée à celle de l'autre. Cependant, en l'état, il ne peut rigoureusement rien se produire, puisque les deux forces s'annulent. La deuxième force voudrait que le segment se brise en son milieu, qui est précisément le lieu où la première force, la force ternaire unifiante, a son foyer. C'est ce qu'exprime le Timée lorsqu'il affirme que "le même et l'autre sont rebelles au mélange". Pour qu'il se passe quelque chose, pour qu'une existence individuelle puisse se manifester, les deux tensions, centripète et centrifuge, doivent s'harmoniser selon deux spirales symétriques, (que l'on pourrait comparer, topologiquement, à la double hélice de l'ADN), l'une rentrante, l'autre sortante, orientées en sens inverse l'une de l'autre, et attachées l'une à l'autre par des coordonnées d'intersection régulières, constituant des foyers de discrétisation, jusqu'à former, si l'on veut, pour nos deux forces, un dispositif de décélération et de neutralisation mutuelle progressive. A ces spirales, finalement réduites à une seule structure, correspond un certain logos, un certain rapport - ou une médiété - entre trois termes, dont chacun (hormis le premier) est à chaque fois le médian de deux autres, qui permet à cette spirale de se dérouler sous la forme d'un escalier discret où, à chaque pallier, se forment certaines catégories de monades. Or, dans le plan ontologique particulier qui est celui de la nature et de la science physique, la médiété qui possède, à l'égard de ces deux tendances fondamentales (et "destructrices" si on les considère individuellement) de la création, la valeur de zéro logique ou de diagonale, et que l'on peut donc considérer comme la position idéale du "frein à main" de la nature universelle sur une échelle graduée; - comme la position qui s'avère, à tous les échelons de celle-ci, génératrice de centres d'accrétion, de "stoppages", d'existences individuelles stables telles que : galaxies, étoiles, planètes, êtres vivants, en un mot comme en cent de monades ou de points, et qui semble par là pouvoir être rapportée au concept, pour nous étymologique, de la Nature comme naissance, engendrement universel, comme à celui plus mathématique de formation; -  cette médiété n'est autre que la médiété Nicomaque 10 ("de Fibonacci"), tendant vers le nombre d'or,  dans laquelle (c-b)/(c-a) = a/b, comme nous espérons le montrer un jour de façon plus détaillée. Sachant que, ce qu'il importe de comprendre en l'occurrence, c'est pourquoi, quand on divise un segment dans le rapport d'extrême et moyenne raison, on ne fait pas seulement de la mathématique, mais aussi de la physique, et ce, à presque tous les étages de cette science; c'est en tous cas le point sur lequel la recherche contemporaine devrait concentrer son attention.

En tant qu'elle fait revivre sous nos yeux, dans sa richesse, l'ancien concept grec de la Nature et de la science physique, science qui se présente d'emblée sous une variété de niveaux et de catégories, mais néanmoins non morcelée, car réunie par un principe transversal, la problématique du nombre d'or a sans doute aussi quelque chose à voir avec un enjeu historique propre à la science occidentale, qui est celui de la réunification de la science physique, ainsi qu'avec l'émergence de nouvelles générations de physiciens, moins spécialisés que ne l'étaient leurs prédécesseurs.

 

*

 

Les forces à l’œuvre dans le secret de l'atome, doivent être les mêmes que celles qui ébranlent la machine du ciel. "Ce qui est en bas est comme ce qui est en haut". Du moins ce chemin est-il le seul qui mérite le nom de science.

 

 

 

Le 10.09.2014

 

 

 

 

ANNEXE

 

 

L'univers a-t-il la structure d'un chou romanesco?

 

 

 

Le nombre d'or n'est pas le fait d'une imagination mathématique mais le principe naturel des lois de l'équilibre.

R. A. Schwaller de Lubicz 

 

 

 

 

 

Selon les données pythagoriciennes que nous venons de développer, la structure de l'univers pourrait être comparée à celle d'un chou romanesco, - structure géométrique à laquelle conviendrait particulièrement, comme on va le voir, le surnom de "mont analogue".

 

 

La structure générale du chou est celle d'un cône, qui est l'expression tridimensionnelle la plus simple de la dyade indéterminée. Le sommet du cône correspond au foyer originaire de la force gravitationnelle, et sa base ou son "embouchure" inférieure, aux limites d'expansion de la force électromagnétique.

Le cône est sillonné par des spirales de Fibonacci rayonnant à partir de son sommet, les unes "lévogyres", les autres "dextrogyres", (habituellement 8 et 13, soit deux nombres successifs de Fibonacci); et sa surface se compose, endomorphiquement, d'innombrables cônes de tailles différentes, tous semblables au plus grand, et eux-mêmes constitués de cônes plus petits, ad perpetuum. Chacun de ces cônes inférieurs, définis par l'intersection de deux spirales antagonistes, correspondant à un "stoppage", à un foyer d'accrétion ou de "retombée" gravitationnelle, et donc à une division ponctuelle et monadologique de l'univers telle que : amas, galaxie, système solaire, planète, être vivant, etc.

Cette structure est abusivement qualifiée de "fractale" alors qu'elle est rigoureusement gnomonique, puisque les spirales sont construites au moyen de rectangles de Fibonacci, et donc de carrés gnomoniques. Or à la différence de la "théorie" des fractales qui n'est qu'une collection de faits mathématiques assez vaguement apparentés, la théorie du gnomon est une véritable théorie mathématique, régie par une loi cadre : la loi du gnomon.

Rappelons que le cône, ou son antagoniste logique : l'entonnoir, affecté d'un tenseur binaire de contraction-expansion, (et entouré d'une sphère), était déjà la structure qui se dégageait avec le plus de vraisemblance du système cosmologique d'Empédocle⁽¹⁾; et la simple forme matérielle du lambda de Platon indique que cette structure est aussi à la "racine" de l'univers du Timée, racine qui est à la fois logique (gnomonique) et musicologique. A la lumière de ces précieux enseignements pythagoriciens, ce légume d'une invraisemblable beauté mathématique, qui nous offre une représentation de l'union parfaite de la monade et de la dyade indéterminée, de la tension ternaire fermante et de la tension binaire ouvrante, et qui n'a sans doute pas fini de livrer ses secrets, mériterait, à coup sûr, d'être étudié avec plus de considération qu'il a pu l'être jusqu'ici.

 

Tous les cônes sont affectés d'une torsion caractéristique, la torsion en "spirales d'or"; en revanche, la distribution géométrique des points de la sphère (circonscrite au cône principal) vers lesquels tendent leurs innombrables sommets, semble, à première vue, générée par un processus  libre ou "aléatoire", un peu comme si chacun des milliers de sommets monadologiques bourgeonnant à la surface du chou (et ce à toutes les échelles de celui-ci) constituait une entité individuelle, dotée d'un mouvement autonome.

 

(05.01.2015)

 

 

⁽¹⁾ Empédocle emploie l'expression : "reflux vers les bords du cercle" pour caractériser le mouvement de l'Un vers le Multiple. La limite d'expansion du Multiple est donc bien un cercle. Dès lors, si l'on veut bien nous concéder que l'univers d'Empédocle n'est pas plat, il est nécessairement conique.

 

 

 

 

 

Références :

Joscelyn Godwin : The harmony of the spheres, a sourcebook of the Pythagorean Tradition in Music

Leon Crickmore : A possible Mesopotamian origin for Plato's World Soul,

A Re-valuation of the ancient science of harmonics

 

  

 

 

 

..........................................................................................................................

 

 

 NOTICE HISTORICO-CRITIQUE :

 

L'ORIGINE DU TIMEE

 

 

Platon plagiaire?

Nous n'avons ni le loisir, ni les moyens de nous intéresser longuement à cette question historique, dans sa dimension potentielle d'enquête policière. Il nous semble que la querelle du Timée repose, à travers les âges, sur un fondement assez simple, qui est le sentiment que Platon n'a jamais fait montre, ni avant, ni après, du génie proprement scientifique qui éclate en quelques passages du Timée.

Les premières accusations précises de plagiat furent lancées, quelques décennies après sa mort, par le talentueux satiriste Timon de Phlionte, cité par Aulu-Gelle :

"Et toi aussi, Platon, le désir du savoir t'a saisi.

A prix d'or, tu t'es approprié

Un mince ouvrage dont tu as pris le meilleur,

Et qui t'a enseigné la timéographie."*

Elles furent ensuite relayées par divers auteurs anciens, tels qu'Hermippe de Smyrne, Satyros, Diogène Laërce, Jamblique, ou Proclus, qui attribuent l'ouvrage, les uns à Timée, les autres à Philolaos, mais aussi modernes, - jusqu'à nos jours. Plutôt discrets jusqu'au XXe siècle, les défenseurs de Platon n'ont, depuis, pas manqué de ressources, puisque l'un d'eux est même parvenu à la conclusion que plusieurs auteurs pythagoriciens de premier plan, comme Philolaos et Timée, n'avaient jamais existé, mais n'étaient que des personnages de comédie inventés par Platon. En raison de la circularité de son principe, il n'est pas rare que la méthode hypercritique, fondée sur la sempiternelle constatation que "nous ne savons rien, ou presque, de ce dont nous sommes professionnellement investis de vous entretenir quand même", accouche assez facilement de l'objet de sa pire hantise, à savoir des élucubrations les plus gratuites. Sans entrer dans le détail de cette controverse qui n'a, en elle-même, d'intérêt que pour les amoureux de Platon, - ou éventuellement pour ceux qui pourraient être aujourd'hui encore tributaires de ce supposé plagiat, en vertu du "déterminisme" inhérent à leur carrière universitaire, comme les rédacteurs de thèses sur le Timée, - on peut se contenter de remarquer qu'un "paquet" assez consistant de concepts pythagoriciens, d'un caractère nettement technique, tels que : paradigme, réceptacle, médiétés, âme du monde, harmonie, solides réguliers, symétrie hexagonale (triangle équilatéral), même, autre, mélange, etc, toutes notions qui sont organiquement subordonnées à la construction pythagoricienne, ou gnomonique, de la gamme musicale, objet de cet article, et que l'on trouve attestées ou corroborées par ailleurs, soit par des témoins solides de la tradition, soit par des éléments constants de la doctrine : - toutes ces notions caractéristiquement pythagoriciennes, donc, font avec le Timée leur apparition groupée dans l’œuvre de Platon, à une époque où celui-ci doit avoir entre soixante-cinq et soixante-dix ans, où il ne lui reste qu'un ou deux dialogues à écrire, et quelques années seulement après la rédaction du Phédon, dans lequel il avait entrepris de démontrer, au prix d'une certaine incohérence doctrinale, que la conception pythagoricienne de l'âme comme "harmonie" - qui est le postulat de base du Timée - était logiquement inconsistante, et qu'on devait lui préférer de beaucoup la conception de la connaissance comme réminiscence, (pourtant elle-même empruntée par Platon, selon toute vraisemblance, à la doctrine ésotérique orphico-pythagoricienne, bien qu'elle soit évidemment plus ancienne et à vrai dire sans âge, puisqu'elle appartient au registre des vérités métaphysiques éternelles, auquel s'abreuve tout enseignement traditionnel).

On en conclura assez raisonnablement, peut-être, que la documentation de Platon en matière de théories scientifiques pythagoriciennes demeura, - jusqu'au Timée, -  très en retard sur ce que pouvaient être, par exemple, ses connaissances en matière de pythagorisme ésotérique, ce qui peut s'expliquer par deux raisons principales.

D'une part, la "religion" orphico-pythagoricienne, même si elle relevait du secret initiatique, ne constituait pas un domaine réservé des pythagoriciens, puisque l'orphisme avait d'autres racines sur le sol grec, auprès desquelles on sait aujourd'hui que Socrate et Platon avaient pu recueillir diverses traditions orales; - tandis que tout ce que l'on sait du secret  "sectaire"  et scolaire proprement pythagoricien, est qu'il concernait, en premier lieu, le savoir scientifique : les théorèmes et les démonstrations. Certes, des contacts avaient existé entre l'école de Socrate et celle du pythagoricien Théodore de Cyrène, alors à la pointe du mouvement mathématique; mais, si l'on en juge par le Théétète, qui ne témoigne pas d'une compréhension bien profonde des questions soulevées par la spirale de Théodore, ces contacts ne semblent pas avoir été aussi étroits qu'on le suppose d'habitude. Quant à prétendre, comme certains n'hésitent pas à le faire, que Théodore fut le "professeur de mathématiques de Socrate, Théétète et Platon", cela nous paraît pour le moins abusif, car, si l'on s'en tient au récit de Platon, Théétète, informateur de Socrate, ne semble pas connaître la raison - pourtant très simple - pour laquelle la monstration de Théodore s'était arrêtée au nombre 17.

Mais d'autre part cette relative négligence des questions scientifiques peut s'expliquer par la personnalité même de Platon, auteur qui fut dominé tout au long de sa carrière par des préoccupations d'ordre principalement esthético-moral. Les idées du Bien et du Beau sont en effet les seuls apports réellement originaux de Platon au patrimoine de la réflexion philosophique; et il faut convenir que ces préoccupations ont absorbé l'essentiel de l'effort qu'on a désigné, après lui, par le mot philosophie, avant qu'il ne s'épuise. Car, de fait, à bien y regarder, ce qu'on désigne couramment sous ce nom ne recouvre, la plupart du temps, qu'une certaine esthétique associée à une certaine morale, ou le contraire. Toute proportion gardée, la présence du Timée dans l'oeuvre de Platon peut donc apparaître aussi incongrue que le seraient, par exemple, un article de Gödel ou de Majorana (en l'occurrence : les deux à la fois) introduits par mégarde dans l’œuvre de Nietzsche ou de Bergson; - pour citer, peut-être, les deux derniers penseurs occidentaux à avoir arboré le statut de philosophe avec un semblant de crédibilité, le costume n'étant, manifestement, déjà plus adapté aux spécificités de l'"intellectuel" du XXe siècle, assigné à des tâches plus spéciales. "C'est seulement comme phénomène esthétique que l'existence et le monde sont éternellement justifiés" (La naissance de la tragédie). Avec la franchise qui le caractérise, Nietzsche admet son incapacité pure et simple à concevoir une forme de compréhension plus élevée, de même que Bergson ne pouvait concevoir la réalité autrement que comme une sorte d'"artiste" (L'Evolution créatrice). Et si l'on veut revenir à l'origine de ce mouvement intellectuel, qui prend sa source, comme on l'a dit, dans la philosophie éthique et esthétique de Platon, il faut être bien conscient que, du point de vue de la connaissance métaphysique, qui est celui où s'enracine la doctrine de Pythagore, les problèmes de cette nature, les problèmes éthiques et esthétiques sont, non seulement dépourvus d'intérêt, mais en un sens plus profond, qui demanderait certes à être explicité, ils sont dépourvus même d'existence.

On pourrait nous objecter que d'autres auteurs, comme Kant, ne se sont "révélés" philosophiquement qu'à un âge assez avancé; mais l'argument ne change rien à la possibilité que, pour Platon, cette tardive "révélation" se soit produite à la lecture d'un traité de physique pythagoricienne, qu'il soit l'oeuvre de Timée ou d'un autre. Ajoutons que la construction de ce dialogue, maladroite et contournée, donne l'impression qu'une théorie scientifique de l'univers s'y trouve introduite un peu par hasard, comme une pièce rapportée; - pièce que l'auteur s'est contenté de faire précéder d'un échantillon sans surprise de son catéchisme personnel, selon lequel "Dieu, étant Bon, n'a pu créer le monde que Beau", sans égard pour le fait que la doctrine du Timée relève d'un postulat scientifique, d'un raisonnement hypothético-déductif, où le monde n'est supposé avoir été créé de telle manière, que parce que telle est la manière dont nous pourrions, ici et maintenant, le recréer nous-mêmes : point de vue qui est intellectuellement contradictoire avec ce type d'approche esthético-morale, lequel ne relève en soi que d'une forme assez inférieure de pensée religieuse.

Pour une documentation plus fournie, on pourra s'en remettre à Luc Brisson, auquel a été dévolue, pour la période récente, la mission de défendre les prérogatives supposées de l'auteur Platon, (statut que le principal intéressé, précisons-le, ne semble pas revendiquer explicitement lui-même, en plaçant son récit sous l'autorité d'un pythagoricien italien, plutôt que sous le patronage de "Socrate", qui lui sert habituellement de pseudonyme), et qui a consacré à la question plusieurs articles dûment garnis de références. On pourra remarquer en les lisant que la méthode hypercritique a certains traits de ressemblance avec celle des révisionnistes : rien n'est prouvé, donc rien n'a jamais existé. Ainsi, pour Brisson, il n'est pas prouvé qu'Archytas ait été pythagoricien, et il n'est pas prouvé que le passage du Phédon sur la conception pythagoricienne de l'âme comme harmonie, concerne réellement la conception pythagoricienne de l'âme comme harmonie. A ce régime, nous pourrions aussi nous demander s'il est prouvé que la phrase que nous écrivons en ce moment soit bien réelle.

L'affaire du plagiat de Platon inspire à Brisson une réflexion épistémologique de haut vol sur "la manière dont travaillaient les historiens de la philosophie dans l'antiquité", qui nous donne l'occasion de nous extasier sur la merveilleuse différence qui existe entre leurs méthodes de quasi-primitifs et "nos méthodes scientifiques actuelles". Le ton est donné : nous n'allons pas spécialement prendre connaissance des idées de M. Brisson, mais avant tout bénéficier de l'immense avantage que nous procure la lumière du savoir universitaire moderne, avec ses techniques reconnues et éprouvées. Pour Brisson, en effet, tous les témoignages de l'antiquité sont sujets à caution, et donc, à l'état brut, inutilisables, du fait que leurs auteurs étaient, malheureusement, ignorants de la véritable science historique. Avant même d'être examinés individuellement, ces témoignages doivent donc être regroupés dans un tableau analytique et classés par catégories, en fonction du genre d'aliénation ou de préjugés culturels dont pouvait être affecté leur auteur. Cette méthode, qui pourrait à première vue apparaître un peu simple, s'avère à l'usage d'une efficacité indiscutable. Habitué à se mouvoir à son aise sur les cimes de la philosophie grecque, le professeur Brisson, grâce à son tableau bien conçu, est ainsi parvenu à épingler en un clin d'oeil une bonne douzaine de ces prétendues "autorités anciennes", et à en démasquer la moitié comme de pathétiques affabulateurs, et l'autre moitié comme d'innocents perroquets, conditionnés à répéter ces contes de bonnes femmes. L'autre avantage de cette méthode étant qu'elle nous dispense, en tout état de cause, d'examiner de plus près ces infortunés auteurs et leurs ennuyeux ouvrages, comme elle nous dispense d'essayer de comprendre, par exemple, pourquoi plusieurs d'entre eux ont la manie de se déclarer "pythagoriciens", ou celle, encore plus loufoque, de considérer Platon comme un disciple de Pythagore.

Car en ce domaine, il est bien connu que rien n'est prouvé, et donc, rien n'a jamais existé : ni Timée, ni Archytas, ni Philolaos....ni, davantage, la conception pythagoricienne de l'âme comme harmonie.

Si ces remarques peuvent apparaître sans indulgence, elles ne sauraient occulter le fait qu'une partie importante de l'exégèse "vingtième-siécliste" de l'antiquité philosophique aura été dominée par le préjugé, aussi niais que désastreux, mais encore dominant à notre époque, selon lequel les anciens nous auraient été, à quelque égard que ce puisse être, intellectuellement inférieurs. Dans cette situation, il faut voir une conséquence du règne moderne de l'idéologie scientiste, avec son concept vulgaire du progrès et son culte idolâtre de la fausse "expertise", à laquelle correspond, dans son registre, une fausse exégèse, discours fondé sur une croyance en la magie des méthodes, qui, quoi qu'il veuille saisir, ne rencontre jamais que soi-même, et qu'il importe de bien distinguer de la véritable exégèse qui, elle, consiste toujours au contraire à accueillir les textes anciens dans leur signification naïve et intemporelle, en tant que ce qu'ils avaient à transmettre était important et simple, et peut nous être restitué ici et maintenant, et qui exige donc une sympathie, une intelligence et une implication personnelle du commentateur, bien éloignée d'un quelconque dogmatisme professionnel, jaloux de ses précieuses "méthodes" et, de ce fait même, cuirassé par un "recul historique", une "distance critique" dont on se passerait volontiers, vu leur caractère oppressant de taupinière intellectuelle.

*

Seul Platon, bien entendu, survit à l'épreuve de cette lessive historico-philosophique, révélatrice avant tout d'une compréhension très insuffisante des réalités mathématiques essentielles qui sont à la base du Timée, et qui font de ce traité ce qu'il est en réalité : l'aboutissement d'un immense effort scientifique interdisciplinaire, - musicologique, cosmologique, logique, mais aussi, par induction générale, relatif à la physique fondamentale, - effort commencé avec Pythagore, et poursuivi, par une tradition directe et ininterrompue, pendant cinq à six générations. Dans ce mouvement, le rôle de Platon, non négligeable, aura été de nous transmettre un dossier scientifique, malheureusement incomplet, dont l'origine italienne, à nos yeux comme à ceux de beaucoup d'autres, anciens comme modernes, n'a jamais fait l'objet d'insupportables doutes.

 

 

Platon et Archytas : la rencontre du sophisme et du pythagorisme

Les voyages en Italie de Platon, ses contacts - empreints d'une évidente méfiance mutuelle - avec Archytas et les derniers pythagoriciens italiens qui furent ses contemporains, et selon plusieurs l'achat (bien excusable, car, à sa place, nous aurions fait la même chose), de quelques livres pythagoriciens, lui auront donc, selon toute apparence, permis de combler tardivement ses lacunes en matière de science.

Concernant ses rapports avec les pythagoriciens : même si Archytas a sauvé Platon du péril de mort où l'avait entraîné sa petite politique de "courtisan-philosophe" auprès de la famille des tyrans de Syracuse, (entreprise de longue haleine, puisqu'il a successivement et vainement tenté sa chance auprès des deux Denys, père et fils), on imagine la méfiance, sinon la condescendance que ce pythagoricien pouvait ressentir pour la nouvelle conception de la politique incarnée par Platon, associant la courtisanerie servile à une prétention "théorique" personnelle totalement utopiste - modèle d'"action" qui sera ensuite imité par Aristote auprès de Philippe de Macédoine, (avec plus de réussite, puisqu'au prix d'une renonciation complète à son "idéal théorique"), et qui est le style politique caractéristique de l'idéologie sophiste, mouvement intellectuel athénien auquel Socrate, Platon, et Aristote n'ont jamais cessé d'appartenir; en dépit du déni un peu naïf de la tradition philosophique occidentale à ce sujet 

Aux antipodes de cette conception avant-gardiste de l'intellectuel comme "soliste libéral", Archytas, lui, comme la plupart des pythagoriciens des générations précédentes, était engagé dans une action politique de haut vol, et exerçait les plus hautes fonctions administratives, puisqu'il fut élu à sept reprises stratège de sa ville de Tarente avec les fonctions de roi. - Rappelons que les disciples directs de Pythagore ont régné pendant plusieurs décennies sur une bonne partie de la "Grande Grèce", région du sud de l'Italie dynamisée par un peuplement grec récent, et qui représentait alors pour le vieux monde grec un "nouveau monde", une terre d'aventure et de liberté propice aux expérimentations politiques. Les pythagoriciens contrôlèrent ainsi les puissantes cités de Crotone, Locres, Tarente, Métaponte et beaucoup d'autres, avant un soulèvement généralisé qui les chassa presque partout du pouvoir, hormis dans quelques poches résiduelles, telles que la cité de Tarente justement, à laquelle Platon dut sa survie.

 

Particularité du mouvement sophiste

Les dialogues de Platon relatent complaisamment la manière dont Socrate se livrait, avec les autres principaux "éducateurs" sophistes de son temps, à un véritable trafic de disciples, habituellement sélectionnés selon des critères explicites : de jeunes garçons beaux et riches, - des aristocrates tels que Charmide, Alcibiade ou Platon lui-même ayant été, notoirement, "distingués" selon ces critères. Il y avait là, assurément, un marché loin d'être négligeable, puisque les sophistes étaient réputés percevoir des salaires énormes : jusqu'à 100 mines pour des vedettes comme Protagoras ou Gorgias, soit cent fois le salaire d'un artisan. Ainsi, pour J-L. Périllié, les propos que Socrate tient à Théétète : "Il y en a beaucoup que j'ai donné en cadeau à Prodicos..." se réfèrent à "toute une pratique de mise en circulation des jeunes gens, pour ne pas dire des éphèbes, au sein d'un réseau sophiste." Le prestige de Socrate tenait en partie à une compétition objective existant entre les sophistes, sur le fait de savoir lequel d'entre eux s'était "attaché" les adolescents les plus mignons et les plus riches; car, en dépit de sa laideur légendaire et de ses origines pouilleuses, son tableau de chasse était sans égal. Vue la simplicité avec laquelle Platon en fait état, il n'y a aucune raison de penser que les choses aient changé à son époque, pas plus qu'à celle d'Aristote. Il n'est certainement pas abusif de parler du caractère vénérien - au sens étymologique - de la transmission du savoir en milieu sophiste. Ce sont là des réalités culturelles, propres à ce mouvement athénien, considéré aujourd'hui comme le berceau de la philosophie académique, qui, même si elles sont bien connues, méritent d'être rappelées de temps à autre; d'autant qu'elles offrent un contraste net avec la tradition pythagoricienne, réputée, d'une part, pour son "féminisme" quelque peu bizarre, d'autre part, pour les critères rigoureux selon lesquels étaient orientés et formés les étudiants, en fonction de leurs capacités purement intellectuelles, notamment mathématiques. Ces deux traditions s'avèrent donc antagonistes, même si elles peuvent avoir ça et là des racines communes. Dans la première, la transmission de la connaissance demeure attachée à certains modèles archaïques d'initiation rituelle, d'un type que l'on peut qualifier d'érotico-religieux. Dans l'autre - novatrice sur ce point - la nature purement intellectuelle du savoir scientifique est clairement revendiquée; et c'est donc la science elle-même, avec ses difficultés, qui est seule juge de l'aptitude de quiconque à devenir l'un de ses desservants. Enfin, dans la première, le développement des "écoles" de pensée se réalise sous la forme de petites entreprises professionnelles et commerciales, tandis que, dans la seconde, le développement des systèmes et des innovations personnelles s'accomplit à l'intérieur d'un même monde, qu'on pourrait appeler le monde pythagoricien, au sein duquel les individualités n'ont pas d'importance. Et de fait, aujourd'hui encore, la science pythagoricienne ne peut se comprendre autrement que comme un continuum, au sens mathématique du terme; (ce qui implique aussi, à travers les âges, une amitié et une fidélité, une association de confiances qui ont conduit à définir la nature de Pythagore comme "quelque chose d'intermédiaire entre Dieu et l'Homme") - Quant aux rapports commerciaux et vénaux, la fraternité pythagoricienne s'en était préservée dès l'origine, comme on sait, par une organisation sectaire favorisant un communisme spontané, de type familial. Ces remarques peuvent apparaître un peu simplificatrices; mais elles n'ont pas d'objet plus ambitieux que de pointer quelque uns des aspects par lesquels ces deux cultures sont hétérogènes.

Dans le foisonnement des doctrines issues de la "révolution" sophiste, seul le mouvement cynique représente un foyer de résistance et d'attachement aux formes de la sagesse traditionnelle, notamment par la sublimité de sa doctrine morale, insurpassée à ce jour - morale essentiellement pratique, monstrative, gestuelle, visant à démolir de façon systématique les constructions "idéologiques" de la sophistique, et dans laquelle on peut certainement retrouver l'image de la véritable morale pythagoricienne, aux antipodes de la bouillie insipide que les néo-platoniciens ont prétendu reconstituer, et nous vendre pour telle.

 

La fin de Platon

La véritable histoire intellectuelle de Platon est tout autre que celle qu'on nous raconte. Platon fut, au soir de sa vie, littéralement écrasé par l'ombre de Pythagore, qu'il ne mentionne qu'une seule fois dans toute son oeuvre, et dont il a pu éprouver la prodigieuse fécondité intellectuelle au nombre des disciples qu'il avait conservé de son vivant, jusque dans son entourage le plus proche. De fait, à la mort de Platon, l'académie a fait l'objet d'un véritable "putsch" ou d'une "restauration" pythagoricienne. Le premier acte de Speusippe comme chef de l'académie a été d'envoyer aux oubliettes la doctrine platonicienne des idées, pour réaffirmer que les idées ne sont absolument rien d'autre que les nombres; et ramener tout le monde à l'étude de la décade et de la tétractys. Son successeur à la tête de l'académie, Xénocrate, sera lui aussi un pythagoricien pur sucre, sans héritier il est vrai; puisque l'école effectuera après eux un retour définitif au platonisme; mais c'est sous le règne de ces deux premiers scholarques qu'a été publié l'Epinomis, qui n'est pas seulement un manifeste pythagoricien, mais aussi, de façon assez évidente, un manifeste "anti-platonicien", ouvrage que personne ne songe plus aujourd'hui à attribuer à Platon, mais sur lequel son nom a été apposé par ses propres disciples sans le moindre scrupule... après tout, n'avait-il pas lui-même montré l'exemple avec le Timée? - Plus étonnant encore, on sait moins que l'école d'Aristote a, elle aussi, après la mort du maître, dû faire face à une tentative de subversion ou de putsch pythagoricien, qui n'a dû qu'à des circonstances aléatoires de ne pas connaître le même succès que la précédente, au prix d'une scission ou en tous cas dune "purge" au sein de la troupe des disciples d'Aristote. Et l'on peut aussi se rappeler que la secte pythagoricienne était déjà bien représentée dans la cellule de condamné de Socrate, dans le groupe des derniers amis à lui rendre visite, et prête à organiser sa fuite et son exil, à l'heure où le téméraire Platon soignait son rhume.

 

La doctrine des idées

D'un point de vue pythagoricien, la doctrine platonicienne des idées ne peut apparaître, aujourd'hui comme hier, que comme une construction inutile et confuse, destinée avant tout à recycler la doctrine du nombre à la moulinette de la "moraline" et de l'"esthétine", avec comme conséquence historique fatale, l'abandon de la philosophie naturelle inhérente à la véritable doctrine du nombre, - philosophie qui est, quant à elle, aussi éloignée que possible de quelque idéalisme que ce soit.

 

L'héritage de Platon

Platon n'a pas eu de disciple, en ce sens que ceux qui l'ont côtoyé physiquement, ceux qui l'ont vu vivre, ne se sont affirmés individuellement que par différentes formes de rejet de la pensée platonicienne. Platon n'a donc produit que des émules, des imitateurs, au premier rang desquels Aristote.

En revanche, notre système éducatif actuel, qualifié avec justesse par Jean-Claude Michéa de système d'enseignement de l'ignorance, et héritier d'une longue tradition académique, peut certainement être considéré comme une tentative sérieuse de réaliser l'utopie platonicienne de la République : celle d'une société parfaite cimentée par des mensonges institutionnels.

"C’est donc à ceux qui gouvernent la cité – si vraiment on doit l’accorder à certains – que revient la possibilité de mentir." (La République)

Pour le philosophe Cédric Enjalbert, la réflexion sur le mensonge participe chez Platon à l’établissement de la justice dans la cité idéale. Il est utile aux hommes à la manière d’une espèce de drogue, car il possède les mêmes effets : accoutumance, stimulation et anesthésie, tous propices à tenir les hommes à leur place, comme des animaux dominés, dressés.

Or tels semblent bien être, selon l'évidence, les principes qui ont inspiré depuis quelques décennies l'évolution de nos systèmes d'éducation.

Stratégie que Jean-Claude Michéa résume dans cette formule, parodiant une maxime de Planck sur la vérité scientifique et ses adversaires :

"Le mensonge ne triomphe jamais entièrement par lui-même, mais ses adversaires finiront bien par mourir."

 

 

*La cité de Phlionte fut, avec celle de Thèbes, où l'exilé Philolaos avait reformé une "école" sur ses vieux jours, l'un des centres pythagoriciens les plus importants parmi ceux qui étaient actifs du vivant de Socrate et du jeune Platon. On peut donc tenir pour vraisemblable que Timon ait pu recueillir, dans cette cité marquée par l'influence des pythagoriciens, un certain nombre de documents ou de traditions locales, concernant une affaire de plagiat qui, selon les datations courantes, se serait produite environ trente-cinq ans avant sa naissance.

 

 

 

Référence :

Luc Brisson : Les accusations de plagiat lancées contre Platon.

La particularité de ce texte est qu'il s'efforce de répondre à un problème historique bien précis : l'origine du Timée, tout en s'appliquant, dans le même temps, à en nier l'existence, ce qui implique que ledit problème puisse être "dissous" dans un flot de "rumeurs" du même acabit, toutes également dépourvues de fondement. Le texte obéit ainsi à une "double contrainte" dont il n'est, en soi, pas inintéressant de suivre le développement.