Rectangle de Fibonacci et triangle d'or de Penrose

 

 

RECTANGLE DE FIBONACCI

ET

TRIANGLE D'OR DE PENROSE

  

 deux applications géométriques de la médiété Nicomaque 10

 

  

 

par Guillaume DENOM 

  

 

Pourquoi les ouvrages de la nature
sont-ils si parfaits ? C'est que chaque ouvrage
est un tout, et qu'elle travaille sur
un plan éternel , dont elle ne s'écarte
jamais; elle prépare en silence les germes
de ses productions; elle ébauche par un
acte unique la forme primitive de tout
être vivant ; elle la développe , elle la
perfectionne par un mouvement continu,
et dans un temps prescrit. L'ouvrage
étonne, mais c'est l'empreinte divine dont
il porte les traits qui doit nous frapper.

Buffon

discours de réception à l'Académie Française

 

 

 

 

 

Bien que plusieurs auteurs aient déjà signalé que la « suite de Fibonacci » était une notion connue et définie depuis l’antiquité dans le cadre du système des médiétés, la littérature mathématique contemporaine continue d’utiliser l’expression « suite de Fibonacci », au mépris de la réalité historique, pour désigner cette notion. La plus ancienne trace écrite de cette notion figure dans  l’Introduction arithmétique de Nicomaque de Gérase, soit plus d’un millénaire avant Fibonacci; en outre, Nicomaque nous précise qu’il n’en est pas lui-même le découvreur, sans indiquer à quelle source il l’a puisée.

Si cette occultation historique est fâcheuse, ce n’est pas pour des raisons de « propriété intellectuelle » qui n’ont, en pythagorisme, aucune espèce d'importance, mais pour la compréhension même de la notion dont il s’agit.

En effet, il n’existe pas de définition plus synthétique, ni plus profonde, de la suite de Fibonacci, que celle qui est donnée dans le cadre du système des médiétés, où elle ne constitue qu’un cas particulier, ou, si l’on préfère,  un élément, d’un ensemble qui en compte 12.

Avant d’aller plus loin, rappelons que, dans le système des médiétés,  trois nombres : a, b, c, sont en proportion « de Fibonacci » (c'est-à-dire en « médiété Nicomaque 10 ») si et seulement si ils satisfont entre eux la relation :

(c - b) = a

(c - a)    b

 

*

  

Dans son Dossier Pythagore, Pierre Brémaud signale une propriété très intéressante des nombres de Fibonacci.

 

« Terminons cette liste des propriétés remarquables de la suite de Fibonacci par celle-ci :

              

« La figure suivante devrait convaincre le lecteur de la justesse de cette relation et de la beauté de l’arithmétique géométrique modo pythagorico. »

  

         

     

Pierre Brémaud, Le dossier Pythagore, p 290.

 

La construction de M. Brémaud est en effet des plus intéressantes, puisqu'elle revient à définir une relation constante entre la suite des nombres de Fibonacci et celle des carrés gnomoniques qui leur correspondent, relation constituant une application importante entre la théorie des médiétés et celle du gnomon.

Reconnaissons, toutefois, que cette construction aurait été encore plus belle et pertinente, si M. Brémaud avait disposé ses carrés en suivant la progression d’une spirale logarithmique, comme dans la figure ci-dessous : 

  

               

Dans cette application de la médiété au carré gnomonique, on remarque, en particulier, que les hypoténuses correspondantes aux carrés successifs de la suite de Fibonacci, se trouvent, elles aussi, en proportion « de Fibonacci ».

  

  

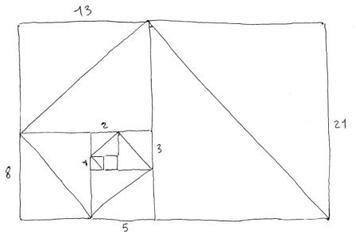
Si l’on prend pour exemple les hypoténuses correspondantes aux carrés de côtés 2, 3 et 5, on vérifie que :

(rac 50 – rac 18)  =  rac 8        =   2

(rac 50 – rac 8)        rac 18            3

Et l'on constate que le rapport a/b qui est le rapport mineur de la médiété (situé à droite du signe égal) est égal au simple rapport des côtés des carrés utilisés, - tout cela en application évidente du théorème de Pythagore.

Enfin, cette construction permet de tracer la spirale logarithmique correspondante à la suite des carrés, spirale rendue célèbre par ses multiples applications « florales » (pissenlit, artichaut, tournesol, etc).

  

   

  

  

*

  

On peut remarquer que la structure de la médiété Nicomaque 10 est constituée, dès l'instant où l'on a disposé les trois premiers carrés (carrés gnomoniques  de rangs 1, 1 et 2), formant ensemble un premier "rectangle de Fibonacci". Le rapport entre la longueur et la largeur du rectangle peut, dès cet instant, être considéré comme une première approximation du nombre d'or, certes grossière, mais qui ne cesse ensuite de se préciser à mesure que la taille du rectangle augmente.

Dans la littérature moderne, la contribution la plus importante, concernant cette médiété Nicomaque 10, me semble être celle de Roger Penrose, avec ses fameux "pavages de Penrose".

On peut dire que la démarche de Penrose est en quelque manière inverse de celle qui est illustrée dans la figure ci-dessus. Alors que, dans la figure ci-dessus, le nombre d'or est la limite vers laquelle tend la croissance du rectangle, dans un pavage de Penrose, ce même nombre d'or est la structure invariante que l'on pose au départ, sous la forme d'un premier triangle d'or, triangle qui, par des divisions successives, engendre un pavage continu non périodique, dans lequel on retrouve la suite des nombres de Fibonacci.

Le "rectangle de Fibonacci" et le "triangle d'or de Penrose" peuvent sans doute être considérés comme les objets géométriques les plus fondamentaux que l'on doive associer à la médiété Nicomaque 10. Entre ces deux objets s'opère un retournement, un retroussement, par lequel toute la nature mathématique se trouve transformée. En effet.

Alors que, dans le rectangle de Fibonacci, la suite de Fibonacci est une fonction de croissance, elle est, dans le triangle de Penrose, une fonction de division. Alors que le nombre d'or est, dans le rectangle de Fibonacci, le nombre correspondant à la position de l'infini, il est, dans le triangle de Penrose, le nombre correspondant à la position "1". Alors que ce qui est "Fibonacci" dans le rectangle de Fibonacci est le nombre de carrés (les nombres de Fibonacci  correspondant au nombre de carrés "atomiques" de valeur 1 que l'on peut dénombrer sur les côtés des rectangles successifs - largeur et longueur), ce qui est "Fibonacci" dans le triangle de Penrose est le nombre de triangles  (obtus et aigus). Le rectangle de Fibonacci contient l'infini, dans ce sens que deux rectangles de Fibonacci ne sont jamais semblables au sens mathématique (le rapport largeur/longueur n'est jamais le même), bien qu'ils soient de moins en moins différents; le triangle de Penrose contient l'infini sur un mode qui est celui de la non-périodicité, c'est à dire que le motif dessiné par un pavage de Penrose ne présente jamais de règle de répétitivité continue, de sorte qu'il est impossible d'en construire l'ensemble au moyen de la réplication d'une partie quelconque.

A ces diverses différences-symétries entre les deux structures, on peut ajouter cette dernière, plus profonde. Alors que, dans le rectangle de Fibonacci, la médiété Nicomaque 10 est une fonction de l'espace, qui s'accomplit dans le temps, dans le triangle de Penrose, la médiété Nicomaque 10 est une fonction du temps, qui s'accomplit dans l'espace.

  

Triangle d'or de Penrose

     

   

 

 La progression du nombre de triangles d'or, aigüs et obtus, est celle de la suite de Fibonacci. Au bout de quelques étapes, on obtient toutes les autres pièces permettant de construire des "pavages de Penrose", à savoir la paire  (fléchette / cerf-volant), et la paire (losange gras / losange maigre). Le triangle de Penrose, constitué de triangles d'or aigüs et obtus, est donc la formule la plus générale, dont dérivent par composition toutes les autres.

  

  *

 

Concluons par deux remarques à caractère plus aphoristique.

 

 Situation du pythagorisme.

Penrose considérait ses pavages comme une récréation mathématique, et n'attribuait pas à ce travail une importance comparable à celle de ses travaux mathématiques "sérieux". De nos jours, l'impact de cette découverte sur la science en général apparaît, au contraire, plus important que celui de ses autres travaux. Ce malentendu est tout sauf anodin, et traduit la situation "problématique" qui peut être celle du pythagorisme dans la science contemporaine.

  

 Le devenir physique des idées mathématiques pythagoriciennes.

 Les pavages de Penrose ont une symétrie d'ordre 5, pentagonale donc, qui était jusque récemment considérée comme interdite dans l'ordre très rigoureux qui est celui des "systèmes cristallins". Un cristal de symétrie pentagonale était considéré comme une impossibilité, parce que le pentagone n'est pas une solution de pavage du plan (et donc, ne peut permettre de construire une facette cristalline). Dans cet ancien paradigme, la contrainte de continuité était associée à la contrainte de périodicité. Au début des années 80, des quasi-cristaux de symétrie pentagonale, présentant toutes les apparences d'un cristal normal, et répondant aux caractéristiques mathématiques d'un pavage de Penrose (continuité non périodique), sont réalisés de façon synthétique*. En 2008, on découvre que, ce que la chimie venait d'accomplir, la nature l'avait déjà réalisé : un quasi-cristal naturel de symétrie pentagonale, probablement d'origine extraterrestre, est découvert en Russie. Ces divers événements ont contraint les manuels de cristallographie à modifier leur définition du cristal, afin d'y intégrer les quasi-cristaux de symétrie pentagonale. Pourtant, la cristallographie pouvait être considérée jusque là comme un département achevé de la physique : édifice entièrement prisonnier des lois de la symétrie, formulées aujourd'hui dans le cadre de la théorie des groupes. La cristallographie est, de fait, une espèce de dimension "témoin" de la physique, interface parfaite entre la structure invisible : les arrangements d'atomes, et la structure visible : la facette du cristal, et son angle au sommet, pure matérialisation de la géométrie des polyèdres.

Là encore, on n'est qu'à moitié surpris. Aujourd'hui comme hier, les idées mathématiques pythagoriciennes semblent affectées d'un certain "devenir physique". La mathématique pythagoricienne implique, parmi d'autres choses,  la recherche d'une certaine adéquation entre la nature mathématique, et la nature physique. Son objet la détermine à décrire, assez souvent, le genre de choses que la nature est susceptible, elle aussi, de réaliser.

 

Septembre 2012

 

*En 2011, Dan Shechtman s'est vu décerner le prix nobel de chimie pour ces travaux sur les quasi-cristaux.

  

              

 Quelques applications florales de la suite de Fibonacci

 

 

                                          

 Structure et aspect d'un quasi-cristal de synthèse

  

   

 

Météorite quasi-cristalline découverte en Russie en 2008

 

  

  

  

GLOSES  

  

 

1. Les médiétés de 1 à 0

 

 
On a vu que la médiété N1 pouvait être définie comme saturée sur un plan sémantique et logique, mais il est également possible de la reconnaître comme saturée sur un plan purement mathématique, puisque le rapport mineur de cette médiété a une valeur constante de x/x = 1, valeur qui coïncide avec l'extension maximale que peut prendre le rapport mineur d'une médiété, les rapports mineurs des autres médiétés pouvant tous s'exprimer par des rapports inférieurs à 1. Dans cette perspective, il peut être intéressant d'élargir notre définition habituelle de la médiété, en définissant le système dans N inclus zéro, et en stipulant qu'une médiété est une relation entre 3 nombres A, B, C, tels que A inférieur ou égal à B inférieur ou égal à C, dans laquelle deux de ces nombres sont entre eux dans le même rapport (mineure) que deux de leurs différences (majeure). On obtient alors 5 niveaux étagés entre 1 et 0.

Niveau 1. La position de référence est donc celle, saturée, de la seule médiété N1 (dite arithmétique) dont le pprm (plus petit rapport mineur possible) est égal à 1.

Niveau 2. Un ensemble de 5 médiétés dont le pprm est égal à 2/3. Ce sont les médiétés N6, N7, N8, N9 et T12. Ces médiétés, auxquelles je ne connais pas d'application géométrique remarquable, donnent l'impression de fonctionner toutes de la même manière et de pouvoir être reliées par une équation commune, de manière à ne former qu'une seule supermédiété.

Niveau 3. Quatre médiétés dont le pprm est égal à 1/2. Ce sont la médiété "géométrique" N2, les médiétés  N4 et N5, ainsi que la médiété T11, que l'on a déjà examinée en raison de son absence d'intérêt mathématique, son adoption se résumant à intégrer dans le système un axiome d'existence du nombre zéro.

Niveau 4. Une seule médiété N3, (dite "harmonique"), dont le pprm est égal à 1/3.

Niveau 5. Dans cette formulation, la position "saturée" qui répond symétriquement à l'autre extrémité du système (où l'envergure est "maximale", c'est à dire égale à 1) est donc occupée par la seule médiété N10 ("de Fibonacci"), dans laquelle le pprm est égal à 0/1 = 0. Puisqu'en effet, notre définition élargie permet d'admettre comme "plus petite solution possible" de la médiété la solution (0, 1, 1), et par suite comme pprm le rapport 0/1. Sur le plan logique, on ne peut donc pas avoir moins de 5 médiétés, semble-t-il.

Précisons que, dans ce raisonnement, on appelle pprm le rapport mineur simplifié, contenu dans la plus petite solution entière d'une médiété; c'est ce rapport qui comporte 5 degrés d'obturation entre 1 et 0. Ainsi, les médiétés du niveau 2 ont, dans leur plus petite solution entière, un rapport mineur égal à 4/6  ou 6/9 (= 2/3). Sur la table des médiétés du blog, les plus petites solutions entières sont reprises de Nicomaque, chez qui elles ne sont pas forcément justifiées par une définition explicite. Pour la médiété "de Fibonacci", Nicomaque retient comme première solution le triplet (3, 5, 8), sans doute pour éviter le triplet (1, 2, 3) qui serait identique à N1. Nicomaque semble donc favoriser la première solution originale d'une médiété; mais rien n'interdit de reformuler la table des solutions à partir d'une définition plus moderne de la médiété, et en privilégiant non plus la première solution originale, mais la première solution possible. Dans ce cas, il paraît donc avantageux de définir le système pour A inférieur ou égal à B inférieur ou égal à C, de manière à intégrer toutes les solutions initiales de la suite de Fibonacci, et notamment les 4 solutions qui précèdent celle retenue par Nicomaque, savoir : (0, 1, 1); (1, 1, 2); (1, 2, 3); (2, 3, 5); ...

   

 

 

2. Obturation du rapport mineur
 

 

La relation logique M (médiété), est une relation biternaire : x/y = M (A, B, C), où x et y doivent être choisis parmi les termes A, B ou C, et où M est le rapport de deux soustractions entre ces trois termes. Dans cette relation, le rapport mineur x/y représente donc le "côté" binaire de la relation.

Dans le système défini plus haut, on peut représenter l'obturation du rapport mineur par l'inscription d'un trépied, ou d'un triangle équilatéral, dans un cercle-unité. Les 12 médiétés se répartissent alors sur 4 positions, puisque les positions de N1 (arithmétique) et N10 (Fibonacci) coïncident, à ceci près que N1 correspond au cercle plein, et "Fibonacci" au même cercle vide. Les positions des médiétés peuvent ainsi recevoir une formulation "angulaire" qui est quaternaire; trois de ces positions correspondant aux sommets du triangle équilatéral, et la quatrième, celle de la médiété N2 (géométrique), étant déterminée par la médiatrice verticale du même triangle. La structure biternaire du système est donc bien apparente, même lorsqu'on ne considère que le rapport mineur. L'axe vertical correspond au côté binaire, le trépied au côté ternaire de la relation.

      

 

  

 

 

3. Table de correspondance

 

Cet article, pourtant simple, a suscité beaucoup de confusions, et notamment l’idée surprenante selon laquelle il pourrait exister des termes manquants dans une fonction mathématique. Il a donc paru utile de dresser une table de correspondance entre les deux structures. 

Il existe, bien évidemment, deux fois plus de rectangles de Fibonacci que de triangles de Penrose, puisque le rectangle de Fibonacci développe les nombres de Fibonacci par paires conjointes, alors que le triangle de Penrose développe ces mêmes nombres par paires disjointes. 

 

 

La série des triangles de Penrose correspond uniquement aux étapes impaires de la série des rectangles de Fibonacci.  Dans le rectangle de Fibonacci, les nombres de Fibonacci correspondent au rapport de la largeur à la longueur (l/L). Le « rectangle de Fibonacci » de rang 1, est donc un « rectangle » de largeur zéro et de longueur 1, c'est-à-dire un segment de longueur 1. Le rectangle de  Fibonacci de rang 2 est un « rectangle » de 1x1, autrement dit le carré atomique de côté 1 (qui permet ensuite de calculer déductivement, visuellement, les valeurs de tous les carrés suivants).  Au rapport (largeur/longueur) du rectangle de Fibonacci, correspond, une fois sur deux, le rapport (triangles obtus/triangles aigus) qui décrit la composition du triangle de Penrose. 

On se convaincra, au vu de ce tableau, que les deux fonctions sont bien complètes, et parcourent la série entière des nombres de Fibonacci, de zéro à l'infini; en précisant que, dans cet article comme dans d'autres, on emploie, par commodité, le terme "infini" dans le sens hyperbolique qui est celui de la mathématique moderne, pour désigner différentes variétés de l'indéfini.

 

 

 

  

  

4. Pentagone de Padovan

  

Si on le considère maintenant, non plus sous le seul angle de sa relation avec la médiété Nicomaque 10,  mais d'un point de vue plus général qui est celui de la théorie des polygones gnomoniques, le rectangle de Fibonacci possède une structure jumelle qui est le pentagone de Padovan.

Alors que le rectangle de Fibonacci est formé de carrés gnomoniques, le pentagone de Padovan est formé de triangles gnomoniques. A chacune de ces structures sont associés une suite arithmétique et un nombre (irrationnel) remarquables (au nombre d'or, phi, de la suite de Fibonacci répondant le nombre "plastique", psi, de la suite de Padovan), ainsi qu'une spirale logarithmique. De la même manière que, dans le rectangle de Fibonacci, le rapport entre les côtés tend vers phi, dans le pentagone de Padovan, le rapport entre deux côtés successifs du pentagone tend vers psi.

 

  

 

 

La suite de Padovan, en revanche, ne relève pas de la théorie "classique" des médiétés à 3 termes, mais d'une théorie plus générale comprenant les médiétés à 4 et 5 termes, ou plus, domaine qui reste largement inexploré si l'on excepte l'étude, par Nicomaque notamment, de la médiété "parfaite", ayant pour plus petite solution le quadruplet (6-8-9-12).

La médiété ci-dessus, qu'on appellera médiété de Padovan, peut, par exemple, être définie comme une relation entre 5 termes : a, b, c, d, e, chacun étant inférieur ou égal⁽¹⁾ à son successeur, dans laquelle on a ces trois identités :

a + b = d

b + c = e

(a + e) = (c + d)

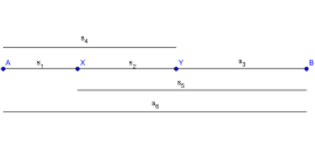
Les cinq termes correspondant aux cinq triangles gnomoniques qui sont suffisants pour délimiter la circonférence de n'importe quel pentagone de Padovan. Dans l'exemple illustré ci-dessus, les termes a, b, c, d, e, correspondent (pour le plus grand des pentagones) aux triangles gnomoniques de rangs : 7, 9, 12, 16 et 21.

Gérard Cordonnier a défini cette médiété en utilisant la méthode euclidienne de division d'un segment en "extrême et moyenne raison", qui permet de définir le nombre d'or. 

  

  

Pour le nombre "plastique", le segment est divisé en trois parties, qui déterminent elles mêmes par combinaison trois autres grandeurs; ces six segments étant tous ordonnés en proportion géométrique. Gérard Cordonnier montre que la proportion géométrique est de valeur : "psi"; ce qui signifie que, tout comme une grandeur peut être "double" ou "triple" d'une autre, chaque segment est ici le "psi-uple" du précédent.⁽²⁾

On voit que les deux méthodes, géométrique et "algébrique", sont équivalentes, puisque tous ces rapports de grandeur sont déductibles des trois identités formulées plus haut. Les segments 1 à 5 correspondent aux termes (a, b, c, d, e) de la médiété, quant au sixième, il correspond au terme "f", terme qui est donc le "successeur immédiat" de la médiété, et qui est toujours égal à (a + b + c) comme cela ressort également de nos trois formules.

  

⁽¹⁾ La mention "inférieur ou égal" permettant, comme pour la suite de Fibonacci, de faire débuter la suite de Padovan à zéro, et d'attribuer pour valeurs au pentagone de Padovan de rang 1, le quintuplet : (0, 1, 1, 1, 2). La série se développe ensuite par quintuplets immédiatement successifs, le pentagone ci-dessus occupant  le rang 10.

⁽²⁾ La très grande généralité de la médiété géométrique fait qu'elle joue ici le rôle de substrat, ou de "paradigme", dans la définition d'une médiété d'ordre moins primitif.