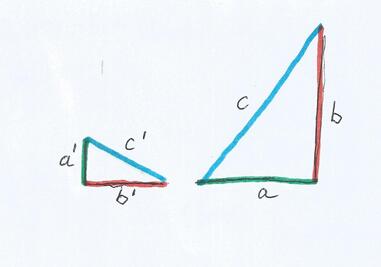LA NEF I - Remarques mathématiques

 

 

LA NEF

 

 

 

A la mémoire

 d'André CHARPENTIER

 disparu pendant que

 nous rédigions ces pages

 qui lui doivent tant

 

 

Sommaire :

 

Prologue

PARTIE I : REMARQUES MATHEMATIQUES SUR LA NEF

chapitre 1 : La hiérogamie

chapitre 2 : La relation d'octave

chapitre 3 : Dans le cercle

chapitre 4 : Les nombres 99 et 9 au cœur du principe d'équilibre de la nef

PARTIE II : LA NEF DANS LES TRADITIONS PYTHAGORICIENNE ET EGYPTIENNE

chapitre 5 : Le nombre de Platon

chapitre 6 : La chambre du roi

Epilogue

 

 

 

 

PROLOGUE 

 

 

 

0.TRIANGLE AURIGENE ET TRIANGLE ISIAQUE : UNE HIEROGAMIE MATHEMATIQUE

 

 

 

 

Loin d'être des inconnus, les deux triangles rectangles dont il sera question dans cette étude ont fait l'objet d'une littérature aussi riche qu'ancienne, forte de multiples occurrences dans les traditions proprement pythagoriciennes ; à ceci près qu'ils ont, le plus souvent, été envisagés de manière séparée, sans que la nécessité de les considérer ensemble, comme formant un ensemble géométrique bien caractérisé, ait été explicitée.

 

A. Le carré long (rectangle de 1x2), que sa diagonale décompose en un couple de triangles aurigènes jumeaux, est l'un des symboles majeurs de ce qu'il est convenu d'appeler la tradition pythagoricienne maçonnique. Au sein de la tradition templière, la peinture murale de Montsaunès atteste que ce même carré long était déjà identifié comme générateur du rectangle de Fibonacci, dont les côtés évoluent en fonction de la suite du même nom ; en précisant que la peinture de Montsaunès précède d'une soixantaine d'années la parution du Liber abbacci de Leonardo Fibonacci. De ces deux perspectives médiévales, la première, la templière, est plus spécialement d'ordre géométrique, tandis que la seconde, celle de Leonardo Fibonacci, est d'avantage d'ordre arithmétique ; mais l'une comme l'autre pouvaient se recommander d'autorités traditionnelles plus anciennes, comme la table des médiétés de Nicomaque de Gérase, dont la dixième médiété définit le principe général des suites auto-additives, dont relève la suite de Fibonacci.

 

B. Le triangle isiaque de côtés (3, 4, 5) se recommande, quant à lui, d'un procès historique de première importance qui est celui de l'antiquité du théorème dit « de Pythagore », connu en toute certitude, autant des mathématiciens égyptiens que des babyloniens. La science moderne, sensible à ce problème historique qu'elle perçoit comme celui de ses origines, reconnaît habituellement à Pythagore le mérite d'avoir produit, ou bien une première généralisation, ou bien une première démonstration de ce théorème, qui l'aurait installé dans la lumière sécurisante et universelle de la science grecque.

 

De fait, énoncer que le triplet (3, 4, 5) est le premier des triplets pythagoriciens, relève d'une pensée scientifique plus développée, abstraite, que celle dont témoignent les traditions plus anciennes, égyptiennes ou babyloniennes, relatives à l'arpentage d'un terrain, au moyen de « la corde à 13 noeuds ».

Il n'y a pas lieu de tomber dans le pessimisme des historiens modernes, selon qui le savoir mathématique serait la conséquence du développement conjoint de « la société » et de « l'économie », en vertu de quoi nous devrions la découverte du théorème de Pythagore à des problèmes juridiques de mitoyenneté entre de gros propriétaires terriens, babyloniens et égyptiens. Car, de ce côté antique, nos connaissances nous permettent de supposer que la doctrine de la corde à 13 nœuds relevait, au minimum, d'une science des fondations de villes.

La notion d'arpentage d'un terrain, et de mesure de la terre, n'était en effet, dans le monde ancien, pas du tout chose pratique et frivole, mais dérivait de ce qu'il est convenu d'appeler une architecture sacrée, régissant les rites de fondations de villes, de sanctuaires, de temples, de maisons, en fonction de l'idée d'une relation entre l'homme et l'univers.

Reste que cette tradition ancienne insiste sur le triangle (3, 4, 5) comme ancrage, à la fois commencement et fin, mesure première et dernière de cette relation de l'homme au monde.

Tandis que la formulation moderne, « pythagoricienne », insiste sur le fait que : « Ceci n'est qu'un début ». Ceci n'est que le départ d'une suite, d'une spirale, intéressante et remarquable en tous les points de son développement.

Au cours de cette étude, nous verrons qu'il existe des explications naturelles à cet état de séparation entre les problèmes A. et B. , comme aussi au fait que, dans la tradition A soit plutôt favorisé le rectangle de 1x2, pouvant être envisagé indifféremment comme formé de 2 carrés atomiques de 1x1, ou de deux triangles aurigènes de (1, 2, rac5) ; tandis que dans la tradition B, la focalisation se fait sur le triangle.

Reste que la démarche de notre étude, au rebours de cet état de choses, sera de montrer qu'il existe une relation mathématique profonde, qualifiée ici de hiérogamie mathématique, entre le triangle aurigène et le triangle isiaque.

 

La première partie de cette étude consistera en une suite de 27 remarques mathématiques, dans lesquelles nous examinerons toutes les modalités de ce mariage, et au fil desquelles nous verrons se préciser la fonction respective de chacun des triangles, dans cette hiérogamie. Nous verrons que le triangle aurigène assume le rôle de principe animateur, et la fonction du centre, tandis que le triangle isiaque endosse le rôle de principe récepteur, et la fonction du champ.

 

Le concept de hiérogamie suppose qu'un couple de dieux ou de symboles quelconque est fécond, en ce sens que leur union produit un troisième, plus riche, plus fort et plus « complet » que le couple « parental » dont il est issu

Dans la seconde partie de cette étude, nous nous mettrons en quête de l'idéologie, à la fois mathématique et cosmologique, à laquelle ces deux principes étaient associées dans certaines traditions de l'antiquité ; et notre attention se portera, de façon toute particulière, sur les traditions pythagoricienne et égyptienne. En filigrane, le lecteur sera invité à prendre au sérieux le principe d'une enquête sur « la formation égyptienne de Pythagore ». Les vies mythiques de Pythagore lui prêtent d'avoir séjourné 20 ans en Egypte, auprès des prêtres de Memphis et Diospolis ; une critique moins enthousiaste admet qu'il ait pu recueillir, au cours de ses pérégrinations, un savoir mathématique égyptien ; et la situation exceptionnelle de Plutarque permet de se rendre compte que, plus de six siècles après Pythagore, la comparaison des mathématiques pythagoriciennes et égyptiennes était encore considérée comme une démarche naturelle.

Au terme de cette enquête, les caractères mathématiques associés dans la première partie à chacun des triangles pourront être ressaisis sous la forme de fonctions universelles, qu'on qualifiera respectivement de « fonction endocosmologique » et « fonction exocosmologique ».

 

 

*

 

Nous sommes loin de la prétention d'avoir fait, sur la nef, les remarques les plus intéressantes ; d'autant qu'il peut y avoir dans cet exercice quelque caractère de nouveauté ; et nous ne nous dissimulons pas le côté un peu rébarbatif que peuvent avoir de tels exposés mathématiques, pour qui n'est pas passionné de choses pythagoriciennes. C'est la raison pour laquelle nous avons ménagé au lecteur deux entrées séparées, pour l'enquête mathématique et l'enquête traditionnelle, en nous efforçant que chacune puisse se lire de façon indépendante. Le lecteur peu friand de mathématiques pourra se contenter de survoler la première partie, ou de lire les énoncés en capitales qui en résument le contenu.

 

 

 

 

 

PARTIE I : REMARQUES MATHEMATIQUES SUR LA NEF

 

 

 

 

CHAPITRE 1 : LA HIEROGAMIE

 

 

 

1. LA NEF SE DECOMPOSE EN UNE CARENE ET UNE VOILURE.

 

La nef est une structure qui réunit le triangle isiaque (3,4,5), prototype de l'ensemble des triplets pythagoriciens, solutions entières du théorème de Pythagore, avec le triangle (1, 2, racine 5), générateur du nombre d'or.

La partie extérieure de la structure, en forme de U, est appelée carène. C'est une tétractys, mais elle est composée de 10 segments, au lieu de dix points.

Nous voyons en effet que, du point de vue arithmétique, rien ne nous interdit de remplacer les 10 segments qui parcourent cette carène par 10 disques – analogues à ceux de la tétractys - dont les diamètres seraient identiques à ces segments. Cette représentation, toutefois, ne serait pas complètement satisfaisante pour l'esprit, puisque certains disques seraient amenés à se chevaucher, alors que les segments ne montrent aucune espèce de recouvrement.

En outre, si nous nous arrêtions là, notre tétractys ne serait pas terminée, au sens mathématique puisque, si les séparations entre les nombres 1 et 2, d'une part, et 3 et 4, d'autre part, sont bien marquées par la forme même de la structure, (précisément, aux endroits-mêmes où des disques se chevauchent) la division entre les nombres 2 et 3, elle, n'est pas encore précisée. Pour pallier ce manque, la carène est donc dotée d'une structure en V appelée voilure.

 

 

 

 

 

 

 

 

2. LA CARENE PEUT ETRE VUE COMME UN PROCESSUS DE CROISSANCE TETRACTYQUE, SE DEVELOPPANT DE GAUCHE A DROITE ENTRE DEUX BORNES.

 

Dans cette représentation, les axes verticaux soutenant les nombres 1 et 4 correspondent à des états de plénitude ; tandis que l'axe horizontal correspond lui, davantage même qu'à la notion d'état, aux idées de d'opération et de médiation entre deux états.

Si on associe les nombres 1 à 4 aux objets monadiques qui leur correspondent – point, segment, disque, boule - ces distinctions s'explicitent très bien. Le point et la boule correspondent bien en effet à deux états analogues de plénitude, le premier, à la plénitude infinie ou puissancielle, et la seconde, à une plénitude partiellement reconstituée, relativement en tous cas à ces formes intermédiaires que sont le segment et le disque.

 

Comme il est naturel, le passage du nombre 1 au nombre 2, qui correspond à une perte de plénitude, s'effectue par une descente, tandis que le passage de 3 à 4, qui correspond au recouvrement de la plénitude, s'effectue par une remontée.

Dans son ouvrage La grande Triade, qui peut être lu comme une vaste méditation pythagoricienne sur le losange associé à la vesica piscis, René Guénon assigne, de la même manière, les nombres 1 et 4 à l'axe vertical, et les nombres 2 et 3 à l'axe horizontal.

 

Dans cette conception, on admet que les positions 1 et 4, soumises au principe de verticalité, correspondent aux bornes d'un processus ; tandis que les positions 2 et 3 correspondent à l'accomplissement, à la réalisation concrète de ce même processus.

Dans cette structure, les segments de valeur 1, 2, 3, 4, qui composent la carène, sont l'image de la complétude de la décade et de la tétractys ; tandis que les nombres racine 5 et 5 qui viennent les couronner symbolisent, à la fois la « quinte essence », et le passage de la puissance à l'acte.

 

3. LA CARENE PEUT ETRE PARAMETREE PAR UN LOGOGRAMME RESULTANT DE LA DIFFUSION DE POINTS DANS UN QUADRILLAGE ORTHOGONAL.

 

 

 

La diffusion de points « activateurs » dans un quadrillage orthogonal régulier et vièrge est un paradigme suffisant pour représenter l'ensemble complet des triplets pythagoriciens, puisqu'il permet de paramétrer les cathètes de ces triangles, dont les hypoténuses sont dépendantes. Toutefois, la famille impliquée par ce paradigme est plus large que celle des triplets, puisqu'elle accueille aussi des triangles tels que le triangle aurigène.

Pour nous, cette représentation a l'avantage de faire converger deux thèmes pythagoriciens caractéristiques : celui du point arithmo-géométrique symbolisant l'unité-position, ou la monade, et qui peut valablement être représenté par un petit disque, comme dans la tétractys, et celui du triangle rectangle et du théorème de Pythagore.

Dans notre cas, ces points pourront être les centres des petits carrés adjacents aux segments-unités qui composent les cathètes, mais il pourront tout aussi valablement être des disques envahissant maximalement la surface de ces mêmes carrés – sans que l'on ait à craindre, cette fois, un chevauchement entre ces disques

Dans cette conception, la « substance » des triangles rectangles pourra donc être représentée par quelque chose qui leur est en somme extérieur : à savoir les petits carrés adjacents aux segments-unités, et les grands carrés adjacents aux côtés des triangles, les relations entre ces petits et grands carrés étant réglées, comme on sait, par la loi du gnomon.

Pour nous, cette représentation présente un double avantage ; elle permet, d'une part, de reconduire les triangles rectangles à un principe monadologique semblable à celui des petits disques de la tétractys ; d'autre part, de soumettre tout triangle rectangle à un principe de carénage qui associe à ses cathètes, non seulement les grands et les petits carrés qui leur sont adjacents, mais aussi les cubes que l'on peut définir à partir de ces carrés ; les uns comme les autres se soumettant à la norme du gnomon.

 

 

 

 

4. LA NEF EST LE LIEU D'UNE TRIPLE RELATION MIROIR.

 

 

Le concept de hiérogamie implique qu'un couple de principes est fécond, du fait que son union produit quelque chose de plus que la simple addition de ses parties. Un tel couple est fécond parce qu'il forme un tout, une nouvelle unité dans laquelle ces parties se dissolvent, perdent leur autonomie antérieure. Pour que cette opération se produise, il faut qu'il existe entre les deux membres du couple certaines relations de réflexivité, qui font que chacun est un miroir pour l'autre, ou que chacun présente à l'autre une image de l'unité supérieure dont ils procèdent.

Notre concept de hiérogamie mathématique enveloppe, on l'aura compris, plus de réquisitions qu'une simple relation de symétrie ; et la présence d'une symétrie, même comprise au sens universel de commensurabilité, entre deux divisions d'une structure, ne suffira donc pas à parler de hiérogamie.

Une hiérogamie est bien plutôt un dispositif dans lequel tombent, de façon organique et profuse, un ensemble bien lié de symétries qui traversent la structure en tous sens.

S'agissant d'une figure plane, il existe quatre modalités principales suivent lesquelles des divisions d'une structure quelconque peuvent se marier, et qui sont :

1. Le haut avec le bas

2. Le dedans avec le dehors

3. La droite avec la gauche

4. La partie avec le tout

 

Ces dimensions de la hiérogamie pourraient être illustrés par des exemples nombreux de symboles, empruntées à maintes traditions ésotériques.

Nous allons voir que la structure de la nef est concernée par l'ensemble de ces relations, à cette nuance près que les dimensions 1 et 2 se présentent en elle de façon indiscernable, dans une situation relevant du choix.

 

• La carène se mire dans la voilure.

  En tant qu'elle est posée sur la carène, la voilure peut être vue comme une structure supérieure, relativement à cette base inférieure ; en tant que ses points sont en moyenne plus proches du centre de la structure, elle peut être vue comme une structure intérieure, relativement à la carène plus extérieure. Et il est possible de combiner ces rapports dans des bi-relations telles que : intérieur-haut (la voilure) et extérieur-bas (la carène) qui communiquent les relations topologiques réciproques de ces deux éléments, relativement au centre géométrique de la structure. 

• La gauche se mire dans la droite – ou le triangle aurigène se mire dans le triangle isiaque, et réciproquement

• Le tout de la Nef se mire dans chacune des parties qui le composent – on peut donc reconstruire l'ensemble de la nef à partir d'un seul des triangles.

 

C'est à l'examen de ces trois formes de réflexivité que seront consacrées nos prochaines remarques.

 

 

 

5. LES VALEURS DE LA CARENE SE REFLETENT DANS CELLES DE LA VOILURE

 

 

On relève, d'abord, cette singularité numérique, que la somme des chiffres de la voilure est égale à celle des chiffres de la carène 5+5 = 1+2+3+4 = 10

 

Autrement dit, « l'extérieur se mire dans l 'intérieur », ou « le bas dans le haut »

 

Mais la particularité de cette égalité entre sommes numérales est qu'elle se greffe sur une égalité géométrique entre sommes vectorielles. En effet, si on considère tous les segments associés à ces nombres comme des vecteurs, alors, en vertu de la relation de Challes, la somme des vecteurs a+b+c+d est bien égale à la somme des vecteurs e+f, puisque les points de départ et d'arrivée sont identiques.

 

 

 

La carène est constituée des cathètes des triangles, la voilure des hypoténuses. Notre remarque « la carène se reflète dans la voilure » peut donc se comprendre comme la mise au singulier d'une expression au pluriel qui serait « les cathètes se reflètent dans les hypoténuses », proposition qui, sous cette forme, fera évidemment penser au théorème de Pythagore.

S'agissant de triangles rectangles, la présence du théorème de Pythagore n'a rien de surprenant ; toutefois, nous verrons dans cette étude que la nef est une structure au sein de laquelle s'expriment des propriétés dérivées de la relation de Pythagore, d'un type particulier, qu'on pourra qualifier de magiques, ou de numérologiques.

La nef est, en outre, une situation dans laquelle une carène formée de dix segments est mise en rapport avec deux autres, qui représentent quant à eux deux modalités du nombre 5 – l'une microcosmique, la racine, l'autre macrocosmique, l'entier. Nous aurons, en son lieu, l'occasion de constater qu'il existe une parenté mathématique substantielle entre le système des hypoténuses de la Nef, et le symbolisme du nombre 515, dans lequel la décade 10 occupe la place de pivot ou de moyen terme entre le macrocosme 500 et le microcosme 5.

 

 

 

 

 

6. LA VOILURE DE LA NEF EST UNE DUALITE AU SEIN DE LAQUELLE LA RACINE 5 SE MIRE DANS L'ENTIER 5.

 

 

 

On voit que, dans la nef,  la zone intermédiaire entre les nombres 1 et 4, considérés comme bornes d'un processus, est toute entière gouvernée par le nombre 5.

Tandis que la base horizontale inférieure de longueur 2+3 peut être envisagée comme exprimant ce processus lui-même, en cours de réalisation, les deux branches de la structure en V jouent l'une pour l'autre le rôle de miroir, où, à gauche, le nombre 5 se présente à l'état de puissanciation, tandis qu'à droite, il s'affirme à l'état d'entier réalisé, mais aussi en tant que retour, ou reproduction de la valeur de la base.

La médiation entre les nombres 1 et 4, considérés comme bornes de la création, se présente donc ici de diverses manières comme une quinte essence, venant coiffer, ou couronner, les essences premières portées par la tétractys.

 

 

 

 

 

7. LA NEF EST PORTEUSE DE DIX SEGMENTS OU RAYONS, QUI SONT LES COUPLES FORMES PAR LES CINQ PREMIERS NOMBRES ET LEURS RACINES

 

 

Les grandeurs racine 5 et 5, qui forment la voilure de la nef, ne forment pas seulement un couple d'individus mathématiques se regardant l'un l'autre, car chacun d'eux se présente comme l'aboutissement, la conclusion d'un processus de construction complet, impliquant la récapitulation de ses étapes précédentes.

En effet, la nef est coextensive à la définition de 10 segments, correspondant à 10 grandeurs ordonnées, au sein d'une relation de dualité généralisée, où le triangle aurigène est porteur des racines des 5 premiers nombres, dont les valeurs entières sont portées, quant à elles, par le triangle isiaque.

 

 

 

Remarquons une différence. Alors que le triangle isiaque contient les 5 grandeurs en son sein, pour le triangle aurigène, on doit passer par la médiation du carré long et de sa vesica piscis associée pour développer la racine de 3.

Les trois cercles nécessaires à la construction ont le même diamètre : 2

On peut remarquer que les dix grandeurs se regroupent tétractyquement, selon certains ensembles naturels :

 

racine 3                                  grand axe de la vesica piscis

1, 2                                        le cercle unité

3, 4, 5                                    le triangle isiaque

rac1, rac2, rac4, rac5            « fibrent » le triangle aurigène

 

Alors que le triangle isiaque porte en lui le principe d'un escalier de 5 marches en progression arithmétique, le triangle aurigène, quant à lui, porte en lui les grandeurs qui correspondent aux 5 premières hypoténuses de la spirale de Théodore ; et l'on remarquera que ce seuil de 5 coïncide avec la première clôture gnomonique de ladite spirale, correspondant au quatrième triangle. Ce micro ensemble théodorien est donc, relativement à la spirale habituelle, dans la même relation qu'un carré gnomonique de rang 2, à l'égard d'un carré gnomonique de rang 4 ; et le statut de bord que possède, dans ce micro système, la racine de 5, répond exactement à celui de la racine 17, pour la spirale classique.

 

 

Mais il faut encore noter que ces deux limites, les racines 5 et 17, entretiennent une relation encore plus évidente. En effet, si l'on compare les aires des deux triangles que ces grandeurs délimitent, le quatrième et le seizième donc, dans l'ordre de la spirale, on s'aperçoit que ces triangles sont dans le rapport d'octave ½

 

 

 

 

 

 

8. CETTE DUALITE A POUR CONSEQUENCE QUE CHACUN DES TRIANGLES EST PORTEUR, A LUI SEUL, DE L'ENSEMBLE DE LA STRUCTURE DE LA CARENE

 

 

Pour le triangle isiaque, on voit qu'il suffit de faire translater vers la gauche du registre les deux grandeurs associées au développement du cercle inscrit, pour reconstituer l'ensemble de la carène. On complète cette carène en n'utilisant que des éléments de la structure interne du triangle isiaque.

 

 

Du côté du triangle aurigène, la façon la plus simple d'exprimer la décadicité de ce triangle est de développer ses carrés adjacents de valeurs respectives 1, 4 et 5

On s'aperçoit alors qu'on peut produire ces carrés en reconditionnant simplement les dix petits carrés adjacents à la carène.

 

 

Et réciproquement, les blocs a, b et c, formant les côtés de la carène, peuvent être obtenus en reconditionnant les carrés a', b', c', qui bordent les côtés du triangle aurigène. Autrement dit : la partie, le triangle aurigène, contient le tout, la carène de la nef, en mode puissanciel.

Le fait de modifier "l'écriture" du triangle aurigène (1,2, racine 5), en exprimant tout en racines, (racine 1, racine 4, racine 5) permet de montrer que les trois côtés du triangle aurigène sont simplement les racines des trois côtés qui forment la carène.

Les cathètes du triangle aurigène pourront donc, avantageusement, être paramétrées de deux manières différentes : un paramétrage interne sous forme de racines carrées, et un paramètrage externe sous la forme de l'entier, qui marque son appartenance comme partie, à la structure entière de la nef.

On a vu dans la précédente remarque que le triangle aurigène était en relation d'octave avec le triangle Théodore 16 pour l'aire ; nous allons voir, dans la prochaine, qu'il est en relation d'octave avec le triangle isiaque pour l'angle, - situation d'intersection que l'on pourra caractériser comme une situation de nouage labdaïque.

 

                                      Aurigène..........................................................Unisson

 

               (relation d'aire)              (relation d'angle)

 

Théodore 16                                                   Isiaque ….......................Octave

 

 

 

 

 

CHAPITRE II : LA RELATION D'OCTAVE

 

 

9. ON DEMONTRE, PAR LA TRIGONOMETRIE CLASSIQUE, QUE LES ANGLES DE LA VOILURE SONT EN RELATION D'OCTAVE

 

 

Pour que les angles de la voilure soient en relation d'octave, il faut, par hypothèse, que :

 

arctan(4/3) = 2 fois arctan(½)

 

Pour l'angle du triangle isiaque, on a les valeurs :

36.87261353367°

53.1340159914°

Qui correspondent respectivement à arctan(3/4) et arctan(4/3)

Ces deux valeurs se proportionnent suivant la formule :

 

 

 

 

où π/2 = 90°

 

La même formule s'applique au calcul de l'angle du triangle aurigène, pour lequel on a les valeurs :

arctan(1/2) = 26.5670079957°

arctan (2/1) = 63.43962152937°

La relation d'octave entre les angles des deux triangles peut être prouvée au moyen de la formule :

 

 

On utilise la seconde formule, différentielle, en entrant nos formules selon le schéma de la nef.

 

1 — 4

2 — 3

 

arctan (1/2) — arctan (4/3) = arctan ( (1/2 - 4/3) ÷ 10/6 )  = arctan (-1/2) = - arctan (1/2)

d'où 2.arctan (1/2) = arctan (4/3)

 

*

 

Quand on cherche à voir in abstracto comment cette formule différentielle pourrait aboutir à cette octave, on cherche en fait à ce que : 

(x + y) / (1 - x.y) = - x

ce qui mène à une équation quadratique en X :

y.X² - 2.X - y = 0

La solution donne X = [ 1 + √(1+y²) ] / y

Une première condition pour que cela se simplifie est que 1+y² soit un carré fractionnaire parfait.

Ce qui est le cas avec y = 4/3

Car alors 1+16/9 = 25/9 = (5/3)²

 

Si y = p/q

alors 1+y² = ( q² + p² ) / q² 

Il faut donc que le numérateur et le dénominateur de y soient liés suivant le lien sacré : que q² + p² soit un carré parfait

 

 

 

 

 

10. LA RELATION D'OCTAVE COMMANDE UN TRIPLET PYTHAGORICIEN

 

 

Notre cas y = 4/3 correspond en fait au triplet isiaque.

Jusque là nous avons raisonné en conditions nécessaires. Si on trouve un triplet pythagoricien, on doit aboutir à un X fractionnaire, qui est effectivement suffisant. Il se trouve que pour le triangle isiaque, cet X fractionnaire se simplifie bien :

X = (8/3) / (4/3) = 2

Essayons à présent avec le triplet (5, 12, 13)

On a donc y = 12/5 et 1+y² = (13/5)²

donc X = [ 1 + √(1+y²) ] / y = 18/12 = 3/2

Si le triplet est (A, B, C)

on aura X = (A+C) / B

par exemple avec (3, 4, 5) : X = (3+5)/4 = 2

Avec (5, 12, 13) : X = (5 + 13) / 12 = 3/2

Pour récapituler : le triplet (A, B, C) génère le couple { y = B/A , x = (A+C) / B } en relation arctan-octavique.

 

 

 

 

11. A CHAQUE TRIPLET PYTHAGORICIEN PREMIER EST ASSOCIE UN LOGOS PREMIER

 

 

Voici la liste des 16 triplets primitifs dont tous les termes sont inférieurs à 100. Si on applique la moyenne A + C / B, on trouve :

 

(3, 4, 5) —— 2:1

(5, 12, 13) —— 3:2

(8, 15, 17) —— 5:3

(7, 24, 25) —— 4:3

(20, 21, 29) —— 7:3

(9, 40, 41) —— 5:4

(12, 35, 37) —— 7:5

(28, 45, 53) —— 9:5

 (11, 60, 61) —— 6:5

(16, 63, 65) —— 9:7

(33, 56, 65) —— 7:4

(48, 55, 73) —— 11:5

(13, 84, 85) —— 7:6

(36, 77, 85) —— 11:7

(39, 80, 89) —— 8:5

(65, 72, 97) —— 9:4

 

Si on poursuit un peu plus loin, pour voir les 16 autres et aller jusqu'à 200 :

 

(20, 99, 101) —— 11:9

(60, 91, 109) —— 13:7

(15, 112, 113) —— 8:7

(44, 117, 125) —— 13:9

(88, 105, 137) —— 15:7

(17, 144, 145) —— 9:8

(24, 143, 145) —— 13:11

(51, 140, 149) —— 10:7

(85, 132, 157) —— 11:6

(119, 120, 169) —— 12:5

(52, 165, 173) —— 15:11

(19, 180, 181) —— 10:9

(57, 176, 185) —— 11:8

(104, 153, 185) —— 17:9

(95, 168, 193) —— 12:7

(28, 195, 197) —— 15:13

 

On remarque deux rapports ultra-décadiques dans le premier groupe, et deux rapports intra-décadiques dans le second groupe, en particulier le triplet (17, 144, 145) qui donne le ton 9:8

Cette organisation générale, qui met en regard des triplets pythagoriciens, un logos, une fraction qui est leur moyenne, possède une analogie évidente avec la structure des médiétés.

Réciproquement, il est remarquable que seul le triplet-racine (3, 4, 5) donne un rapport B/A relativement simple = 4/3. Pour tous les autres triplets, ce rapport est déjà outre-décadique.

On peut trouver étonnant que le sous-ensemble pythagoricien des triplets premiers puisse suffire à produire une base, propre à générer tous les logoï. A priori, la condition rectangulaire ne pourrait-elle "laisser des trous"?

On remarque en outre que :

(B+C) / A génère des entiers

tandis que

(A+B) / C est une fraction irréductible

 

 

 

 

12. LA RELATION D'OCTAVE DANS LES ANGLES DE LA VOILURE SE DEMONTRE AUSSI PAR LA TRIGONOMETRIE RATIONNELLE

 

 

La trigonométrie rationnelle fournit un moyen de prouver le loi d'octave dans la nef, sans utiliser ces arctan qui peut déranger par son caractère excessivement abstrait.

 

La trigonométrie rationnelle est une reformulation de la trigonométrie classique et de ses fonctions transcendantes sinus et cosinus. Plutôt que les distances et les angles, cette géométrie utilise la quadrance et le spread. La connexion avec les concepts de la trigonométrie classique se fait par les relations :

 

• La quadrance = distance au carré

• Le spread = sin(angle) au carré.

 

Le spread entre deux faces des solides réguliers est un nombre rationnel, et leur inverse est musical :

• 1 = unisson

• 9/8 = ton

• 9/4 = 9/8 = ton

• 5/4 = tierce

 

 

 Indépendamment de leur équivalence avec les concepts de la trigonométrie classique, les concepts de la trigonométrie rationnelle possèdent des applications naturelles qui leur sont propres, et semble-t-il, de portée plus puissante. Notamment, le spread mesure l'écartement entre deux droites, depuis le rapport parallèle (0) jusqu'au rapport perpendiculaire (1), indépendamment du "quadrant" choisi.

 

Dans le cas qui nous intéresse, le spread correspondant à 30° = 1/4, 45° = 1/2, 60° = 3/4.

On voit donc que dans cette perspective quadratique, 30° + 30° = 60° mais 1/4 + 1/4 = 1/2

Dans cette approche, on devine que le théorème de Pythagore devient encore plus simple.

 

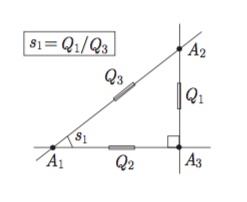
La définition ci-dessus permet de dire que, pour le triangle aurigène : s = 1/5.

Et pour le triangle isiaque, s = 16/25.

Une formule de base dit que r = 4s(1-s).

 

 

Appliqué à la nef :

4s(1-s) = 4.1/5.4/5 = 16/25

Ce qui prouve que l'angle du triangle isiaque est double de l'angle du triangle aurigène.

 

 

 

 

 

13. LA STRUCTURE DE LA NEF MET EN EVIDENCE UN RAPPORT DE GEMELLITE ENTRE LE RAPPORT D'OCTAVE ET LE NOMBRE D'OR.

 

 

 

La formule (A+B)/C par laquelle on génère les logoï associés aux triplets pythagoriciens, si on l'applique au triangle aurigène, engendre le nombre d'or. On peut donc dire que le logos phi se présente comme un cousin des logoi naturels générés par les triplets, au sein d'un famille plus large.

 

 

(a+c)/b = 2/1

(a'+c')/b' = Φ

 

Quant aux logoi générés par les triplets, ils se signalent, avant tout, par leur caractère de primarité ; on peut donc les voir comme des parents des nombres premiers, avec les caractéristiques que cela suppose, comme l'impossibilité de récurrence d'un logos dans la suite générée par nos triplets, et donc un principe de création continue.

La nef est donc une structure qui fait correspondre au logos 2/1 du triangle isiaque, le logos phi du triangle aurigène ; logoï qu'elle nous présente dans un rapport de gémellité.

 

 

 

14. LES AIRES DES TRIANGLES DE LA NEF SONT EN RELATION « SOLAIRE » 1/6

 

 

L'aire du triangle aurigène est égale à 1 ; c'est à dire qu'elle est égale au petit carré insécable de surface 1 qui est l'unité atomique du système. L'aire du triangle isiaque étant égale 6, la surface totale de la nef vaut 7.

Cette relation pourra faire penser à la structure des pavages hexagonaux, dans lesquels un élément (un hexagone, ou un cercle) est entouré de six autres ; en considération de quoi le triangle aurigène pourra nous apparaître une nouvelle fois comme "intérieur", par rapport à un triangle isiaque "extérieur".

Les deux triangles (qui comme on le sait, sont des demi-rectangles) ont la propriété que leur aire respective peut « à nouveau » être formulée sous la forme d'un rectangle.

 

On a vu que l'aire du triangle aurigène était égale à celle d'un carré atomique de côtés 1x1 (un carré étant un cas particulier de rectangle). Tandis que l'aire du triangle isiaque est égale, quant à elle à celle d'un rectangle de 2x3 = 6 ; autrement dit, elle se compose de 6 petits carrés du type qu'on vient de définir.

 

Mais de la même manière que les aires des triangles de la nef peuvent être « converties » en des aires équivalentes de quadrilatères, on voit qu'elles pourraient l'être au moyen de disques atomiques de diamètre 1 remplissant les petits carrés dont ces quadrilatères se composent, dont les rapports mutuels de quantité et de surface seront toujours proportionnels à ceux de ces carrés.

Le rapport des aires des triangles de la nef, correspondra alors au rapport d'un disque à une constellation de 6 disques disposés autour de lui de la manière suivante :

 

Les deux système d'équivalence sont d'une égale légitimité arithmétique ; toutefois, le système fondé sur des cellules discoïdales fait apparaître un rapport de complémentarité plus parfait entre les aires des triangles : puisque celles-ci correspondent alors, respectivement, au cœur et à la couronne d'un système cellulaire hexagonal.

 

 

CHAPITRE III : DANS LE CERLE

 

 

15. SI L'ON CONSIDERE, NON PLUS LES TRIANGLES DE LA NEF, MAIS LES RECTANGLES FORMES DE DEUX TRIANGLES JUMEAUX, LA RELATION SOLAIRE 1/6 S'EXPRIME PAR UN SYSTEME DE PAVAGE PROGRESSIF DU PLAN, OU LE CARRE LONG EST L'ELEMENT ATOMIQUE DONT EST CONSTITUE LE RECTANGLE ISIAQUE.

 

Le mariage se poursuit à la deuxième génération, où l'on considère, non plus des triangles, mais des rectangles, les rectangles 1x2 et 3x4, générés par nos triangles primitifs.  

 

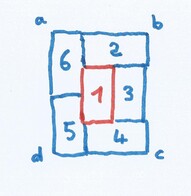
On observe en effet une relation très simple entre ces rectangles : on peut construire un rectangle isiaque à partir d'un "coeur" aurigène, par un pavage en spirale continu. Le rectangle isiaque correspond à la première "clôture", au premier tour de spirale.  On peut penser ici au symbole du G maçonnique.

 

Le rectangle abcd formé de 6 rectangles aurigènes, est isiaque. Le ratio 1/6 qui s'exprimait en extériorité dans la nef triangulaire, se présente ici comme un rapport endomorphique, dans lequel l'un des termes est une partie de l'autre.

La spirale se prolonge à l'infini. De ce fait, les hypoténuses racine 5 et 5, correspondant aux deux premiers rectangles, apparaissent comme les 2 premiers termes d'une série infinie, dont les suivants sont racine 61 et racine 113, suite formée, suivant le théorème de Pythagore, par les racines des sommes des carrés des paires d'entiers consécutifs (impair, pair).

 

 

Le passage du triangle au rectangle, par duplirotation, ou son dédoublement en en couple de jumeaux, est intrinsèquement lié au fait d'inscrire le triangle dans un cercle, puisque, mathématiquement, l'opération revient à interpréter l'hypoténuse du triangle comme le diamètre d'un cercle - comme nous le verrons plus en détail dans la prochaine remarque, avec Lima De Freitas. La suite des hypoténuses générées par la progression du pavage en spirale, peut donc également être vue comme une suite de cercles concentriques, générés depuis le premier, de diamètre racine 5.

 

 

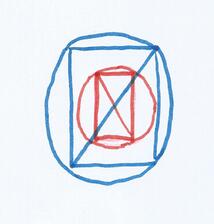
Si l'on considère les deux premiers rectangles comme formant un ensemble fermé, on remarque que le carré long se manifeste sous la forme d'un complexe de fonctions « initier, centrer, paramétrer » ; tandis que le rectangle isiaque se présente sous la forme d'un complexe « développer, cadrer, périmétrer ».

On pourrait estimer qu'il y a « retour » de la forme rectangulaire dès l'étape 3 du pavage ; néanmoins le trajet accompli n'a encore que la forme d'un U ; et c'est seulement à l'étape 6 qu'est perceptible une clôture ayant la valeur d'un recommencement logique, d'un tour complet de spirale correspondant à « l'obtention d'un niveau supérieur ».

Du point de vue de l'évolution du rectangle, le point de départ est l'octave (carré long de 1x2); tandis que la limite vers laquelle tend la suite est l'unisson (carré de rapport 1x1). Ce qui pourrait constituer une explication simple de l'appellation paradoxale "carré long".

Si l'on regarde l'évolution de la surface du rectangle, mesurée en carrés longs, on trouve la suite : 1, 6, 15, 28....   soit la série des nombres hexagonaux, qui sont les nombres triangulaires de raison impaire.

On peut se demander si l'hypoténuse racine 25 du triangle isiaque est la seule à valeur entière (5), ou s'il en existe d'autres, plus loin dans la série. Parmi les 16 premiers triplets pythagoriciens (a, b, c), il n'en existe aucun dans lequel a soit impair, et b égal à a+1, conditions requises pour qu'un triplet s'intègre dans la série. Plus loin, on rencontre le triplet (119, 120, 169) qui remplit les conditions requises, et dont on peut estimer qu'il constitue le second membre d'une famille.

Famille réduite ! Sur cette page la section 3.2 The Two Legs are Consecutive. donne cette liste :

3, 4, 5     20, 21, 29     119, 120, 169     696, 697, 985

Mais surtout la manière de les générer. Et, pour commencer, le plus petit côté doit appartenir à cette suite : http://oeis.org/A001652

0, 3, 20, 119, 696, 4059, 23660, 137903, 803760, etc...

Si maintenant on ajoute la condition "plus petit côté impair", on aboutit à :

Z = 3, 119, 4059, 137903, etc...

Le triplet est donc de la forme : (z, z+1, y)

avec y obéissant à la condition de Pythagore.

Remarquons que le rapport entre membres de la fratrie se concentre dans l'intervalle (33, …, 34). En dehors du premier 119/3 qui est un peu « excentré », 4059/119, 137903/4059, et le suivant rentrent dans cette fourchette.

 

 

 

 

 

16. UNE REMARQUE DE LIMA DE FREITAS SUR LE TRIANGLE ISIAQUE ET LE 515 RENVOIE PAR DEDUCTION AU TRIANGLE AURIGENE ; LES DEUX TRIANGLES ETANT, SOUS LE RAPPORT DU DEVELOPPEMENT DES CARRES ADJACENTS, DANS LA RELATION D'UN NOMBRE A SON CARRE

 

 

Dans son étude sur le symbolisme du nombre 515, Lima de Freitas remarque que le cercle circonscrit au triangle isiaque permet exactement que se développe un second triangle isiaque, jumeau du premier - propriété commune à tous les triangles rectangles.

 

 

« Cette duplication, observe-t-il, entraîne la superposition des hypoténuses », ce qui convainc notre auteur de les additionner numérologiquement : 5+5 = 10 = 1+0 = 1

De Freitas observe ensuite que si nous procédons à « la mise au carré des côtés 3 et 4 des triangles inscrits, nous obtenons le nombre 25 de chaque côté de l'hypoténuse commune. » Or : « l'extraction de la racine carrée de ces nombres 25, 1, 25 fournit 5, 1, 5, autrement dit, le chiffre de l'envoyé de Dieu. »

Pour notre part, nous pensons qu'il est géométriquement plus juste d'interpréter la mise en rapport des deux hypoténuse, non pas comme un processus « additif », mais comme un rapport fractionnel ; ce qui du reste, ne change rien au résultat puisque 5/5 = 1

L'intérêt de cette manière de voir est que, si l'on applique maintenant le raisonnement de De Freitas, non plus au triangle isiaque, mais au triangle aurigène, on obtient en lieu et place des valeurs 25, 1, 25, les valeurs 5, 1, 5 elles mêmes ; ce qui est bien naturel, puisque, du point de vue du développement des carrés adjacents, le triangle aurigène est précisément au triangle isiaque dans la relation d'un nombre à son carré.

Pour être plus complète, cette remarque aurait dû évoquer, dans les pas de Lima De Freitas, le symbolisme du nombre 55, dixième nombre triangulaire et valeur secrète de la tétractys ; mais du fait de l'ampleur du sujet, nous ne pouvons qu'en renvoyer l'examen à une autre occasion.

 

 

 

17. LA HIEROGAMIE DES TRIANGLES S'ILLUSTRE, DE DIVERSES MANIERES, PAR LES MODALITES DE LEUR INSCRIPTION COMBINEE DANS LE CERCLE

 

 

Le triangle isiaque admet un cercle inscrit, dont le rayon et le diamètre correspondent aux cathètes de son compagnon naturel : le triangle aurigène.

 

 

Une construction due à Jain 108 accouple le triangle isiaque au triangle aurigène, mais cette fois dans le cercle circonscrit. Que ce soit par le « dedans » ou le « dehors », par le cercle inscrit ou le cercle circonscrit, le triangle isiaque rencontre « immédiatement » son compagnon aurigène, auquel il est structurellement lié.

 

 

En vision aérienne, les points d'incidence du triangle isiaque avec le cercle induisent une partition de ce dernier, que l'on peut exprimer de manière approximative par le rapport 2/3

En effet, l'angle AÔC mesure environ 73°, c'est-à-dire environ 40/41% de 180°, soit une répartition 40/60 — c'est à dire 2/5 et 3/5, ratios dont résulte cette division quasi-décadique du cercle.

 

 

En développant le dessin de Jain 108, on peut aussi envisager une construction qui combine les 2 constructions, avec les cercles inscrit et circonscrit :

 

 

Pour reprendre les choses en vue aérienne, cette construction revient à « tétractyser » le cercle ; et, par ce biais, à le raccorder au « schéma » de la nef, en tant que construction qui distingue au sein de la tétrade deux groupes 1-4 & 2-3. Le petit bitonio bleu indique le report au compas de la longueur 2, pour construire le 4, ce qui aboutit à faire apparaître le 1, en noir, à la suite de ce dernier.

 

 

En dernier lieu, il est possible d'ajuster ensemble le carré long et le rectangle isiaque dans un même cercle, de manière à ce qu'ils possèdent une diagonale en commun, qui dans notre dessin est la diagonale rouge.

 

La diagonale rouge vaut en effet rac5 en tant qu'elle appartient au carré long (en bleu), et 5 en tant qu'elle appartient au rectangle isiaque (en vert). C'est la voilure de la nef qui se trouve fusionnée ici en un seul objet, qui est le diamètre générateur du cercle. Pour exprimer cette conjonction nous distinguons les deux rectangles par deux normes différentes : romaine pour les valeurs du rectangle isiaque (III, IV, V) et arabe pour celles du carré long (1, 2, rac5).

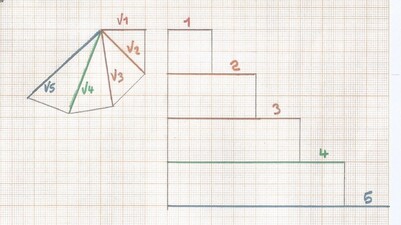
On remarquera à présent que le fait de « plonger » le carré long dans un rectangle isiaque a pour effet d'engendrer 3 nouveaux types de triangles aurigènes, différents du triangle primitif ODX dessiné en bleu. Ce sont, en ordre croissant :

Un petit triangle MNX, dont le grand côté de l'angle droit est ajusté au petit côté d'un moyen triangle MDX, lui même ajusté, par son grand côté, au petit côté d'un grand triangle ODM.

Ces trois triangles sont donc en proportion d'octave continue.

On pourrait penser ici aux tabliers maçonniques, qui ressemblent à une enveloppe pliée, et qui représentent, nous semble-t-il, le grade de maître. Le signe du compagnon serait un triangle qui vient occuper un angle de l’enveloppe en la « diagonalisant ». Autrement dit, le compagnon raccorde « par les côtés » et le maître « par l’hypoténuse ».

 

*

 

Notons enfin que cette dernière figure est structurée par un chrisme.

Au centre du dessin, en effet, se croisent chrismatiquement 3 diagonales de couleurs différentes, dont deux appartiennent en propre à chacun des rectangles, tandis que la troisième, la rouge, leur est commune.

La ligne verticale possède la valeur de racine , de méridienne qui génère — via les deux triangles bleus jumeaux — la croix, ou carré oblong de saint André : les V

Cette méridienne entre les V se lit par ailleurs « V √ V »

La double nature du V semble impliquer la capacité de conversion de cette croix.

Après la procession, le "bleu du ciel" s'évanouit, et il ne peut être retrouvé que par une sorte de mémoire.

La mémoire que ce V est aussi √5 — régénérant la racine verticale en ascension.

 

 

 

 

 

CHAPITRE IV :

 

LES NOMBRES 99 ET 9 AU COEUR DU PRINCIPE D'EQUILIBRE DE LA NEF

 

 

 

 

18. AUX NOMBRES 9 ET 11 SONT ASSOCIEES DES FONCTIONS LINGUISTIQUES QUI SONT RESPECTIVEMENT LA FONCTION ANAGRAMME ET LA FONCTION PALINDROME

 

 

Les multiples des nombres 9 et 11, que l'on pourra regarder comme leurs descendants, sont associés à deux fonctions bien caractéristiques, en particulier parce qu'elles sont aussi des fonctions de langue.

Au nombre 9 est associée la fonction qui veut que tout anagramme d'un multiple de 9, est aussi un multiple de 9. Les descendants du nombre 9 sont donc assujettis à une relation de cousinage étroit, qui veut qu'en mélangeant les chiffres dont ils se composent, on obtient toujours un cousin, c'est à dire un nombre qui est aussi un multiple de 9.

Tout multiple de 9 appartient donc à un groupe familial étroit, formé de l'ensemble de ses anagrammes, mais aussi à l'ensemble universel des multiples de 9, dont il porte « la marque », le nom de famille pourrait-on dire. En effet, si on fait la somme des chiffres dont se compose un multiple de neuf, puis la somme des chiffres de cette somme, jusqu'à exhaustion du processus : on retombe immuablement sur le nombre 9. Cette fonction peut être associée à l'idée de conservation ; en ce sens que tous les descendants du nombre 9 sont « reconductibles » et en quelque sorte « solubles » dans la matrice dont ils sont issus.

Au nombre 11 est associée une fonction palindrome, dont chacun connaît le principe d'application linguistique, mais qui, en mathématique, est susceptible de plusieurs définitions, comportant différents degrés de généralité.

a) Selon une première définition, un nombre palindrome est un nombre qui est invariant lorsqu'on intervertit son premier chiffre avec le dernier, le deuxième avec l'avant dernier, et ainsi de suite, et s'il y a lieu, celui du milieu avec lui-même. Selon cette définition, les nombres 1 à 9 sont tous palindromes, et le premier nombre non palindrome est le nombre 10.

b) Un palindrome généralisé est un nombre qui est palindrome selon la définition a) lorsqu'on l'a amputé de ses zéros terminaux. Selon cette définition, les nombres 10 et 110, par exemple, sont palindromes, et le premier nombre non-palindrome dans la suite des entiers est le nombre 12 – ce qui peut sembler naturel, si l'on remarque que ce nombre exprime formellement la dyade ou la différence pure.

c) Enfin, on peut donner de la fonction palindrome une définition plus restrictive, selon laquelle, d'une part, ne sont pas reconnus comme palindromes les palindromes généralisés, d'autre part, ne sont reconnus comme palindromes que les nombres dans lesquels « un mouvement d'interversion a réellement eu lieu », ce qui exclut les nombres singletons de 1 à 9, pour lesquels ce mouvement est nul, voire inexistant. Selon cette définition restrictive, le premier nombre réellement palindrome est le nombre 11, et ses premiers successeurs ne sont autres que ses multiples, les nombres 22, 33, …, 99. C'est à cette définition restrictive que nous aurons recours dans les remarques suivantes.

Nous pouvons d'ores et déjà relever une première différence entre les deux fonctions.

La fonction anagramme, la fonction du 9, opère au sein d'une famille de nombre, qu'elle assujettit à un principe de communauté et d'unité, tandis que la fonction palindrome opère au sein d'un nombre particulier. Les deux fonctions peuvent être vues comme des principes de liaison, mais alors que la fonction anagramme concerne la liaison d'un nombre avec une famille, la fonction palindrome est une liaison qui s'opère au sein d'un nombre particulier, entre des parties de lui-même.

 

 

 

 

19. LES DEUX FONCTIONS SONT DIALECTIQUEMENT LIEES

 

 

Nous allons voir, à présent, qu'en dépit de cette différence, les deux fonctions sont intimement liées l'une à l'autre.

Commençons par nous doter d'une définition de la fonction anagramme. Un anagramme est un nombre que l'on a obtenu en mélangeant les éléments d'un autre nombre. Ainsi se trouve pointée cette « relation à l'autre » qui caractérise la fonction.

Il nous saute immédiatement aux yeux qu'un nombre palindrome, dans lequel on peut intervertir la moitié des éléments avec l'autre, n'est rien d'autre qu'un cas saturé de la fonction anagramme qui est « le mélange a effet nul ». La fonction palindrome peut donc, sous ce regard, être vue comme une sorte de « degré zéro » de la fonction anagramme.

Mais voici maintenant autre chose.

Si l'on prend un nombre quelconque de la famille des multiples de 9 (possédant autant d'anagrammes que de solutions de mélange entre ses éléments) et qu'on le soumet à une opération de duplirotation positionnelle, on engendre un nombre palindrome, qui, dans l'ensemble universel des multiples de 9, correspond à un groupe de cousins « deux fois plus gros » que ceux de la famille à laquelle appartenait le nombre de départ. De cette manière, par exemple, à partir du nombre 432, on engendre, par duplirotation, le nombre 432234, multiple de 9, et qui peut lui même être vu comme le représentant d'une nouvelle famille de nombres anagrammes les uns des autres, plus « spacieuse » que la première, et comprenant tous les mélanges possibles entre les éléments de ce nombre à six places, tels que : 223344, 443322, 234234, 432432, etc, etc.

Ce principe de développement qui, à partir d'un multiple quelconque de 9, permet, par duplirotation, la création d'une famille anagrammatique plus spacieuse, est bien évidemment indéfini, puisqu'à partir du nombre 432234, on peut à nouveau engendrer, par duplirotation, le nombre 432234432234 qui pourra, à son tour, être vu comme le représentant d'une nouvelle famille anagrammatique.

Notons que cette fonction de dédoublement n'est pas une fonction au sens vague dont nous avons fait usage jusqu'ici, suffisant pour caractériser une opération linguistique, mais une fonction mathématique au sens strict, puisqu'elle associe biunivoquement, à tout élément d'un ensemble de départ, un et un seul élément d'un ensemble d'arrivée. C'est à cette fonction que nous aurons recours tout-à-l'heure, dans l'analyse des pentagrammes pythagoriciens.

Récapitulons. D'une part, un palindrome n'est qu'un anagramme à effet nul. D'autre part, le principe de duplirotation qui régit la structure interne d'un nombre palindrome, est, pour la famille des multiples de 9, un principe de déploiement et d'élargissement, qui permet, à partir de tout multiple de 9, de générer des familles de plus en plus spacieuses de multiples de ce même nombre.

Les deux fonctions entretiennent donc une relation bien particulière, en vertu de laquelle, la fonction palindrome représente, pour la fonction anagramme, à la fois un principe de mouvement à effet nul, et un principe de développement indéfini.

 

 

 

20. LE NOMBRE 99, « LE PREMIER ET LE DERNIER », EST L'AXE DE BASCULE DES DEUX FONCTIONS

Le lecteur qui nous a bien suivi jusqu'ici remarquera que le nombre 99 est à la fois :

 

• Le premier multiple de 9 qui soit palindrome au sens restrictif énoncé dans la définition c)

• Le dernier membre d'une famille très étroite de multiples de 11, dont tous les membres depuis le premier sont des palindromes stricts, au sens de la définition c)

 

En effet, au delà du nombre 99, la famille continue des multiples de 11 qui sont des palindromes stricts s'interrompt, puisque le successeur de 99, le nombre 110, n'est pas un palindrome strict, mais un palindrome généralisé.

Le nombre 99 est donc le premier multiple de 9 qui soit palindrome, et le nombre qui clôture une famille fermée de nombres successifs, qui sont à la fois multiples de 11 et palindromes stricts.

Ce statut de « premier et dernier » confère au nombre 99 un rôle évident de pivot, ou de bascule, qui fait coïncider la fin d'un processus, avec le départ d'un autre.

Notons (pour nous en souvenir dans la seconde partie de cette étude), que ce statut bivalent du nombre 99, qui le caractérise comme « premier et dernier », peut être rapproché d'un autre complexe d'idées qui est celui de l'entrée et de la sortie. En effet, le nombre 99 peut être vu, pour la famille des multiples de 9, comme le point d'entrée ou de « rencontre » de cette famille avec la famille des nombres palindromes (au sens strict) ; tandis que, pour la famille des multiples de 11, ce nombre marque la « sortie » d'un ensemble bien lié, et sans trou, qui rassemble «  les successeurs immédiats du nombre 11 qui sont comme lui des palindromes stricts ».

 

 

 

21. UN ECRIT GNOSTIQUE, L'EVANGILE DE VERITE, APPORTE UN ECLAIRAGE COMPLEMENTAIRE SUR LA FONCTION DE BASCULE DU NOMBRE 99, QUI MET EN JEU SON STATUT DE PREDECESSEUR DU NOMBRE CENT

 

Cet extrait d'un écrit de la bibliothèque de Nag Hammadi développe une comparaison entre le nombre 99 et le jour du Sabbat, qui est le dernier jour de la semaine, et à ce titre, celui de « la bascule ». Son symbolisme s'appuie sur un ancien système de compte sur les doigts, dans lequel, jusqu'au nombre 99, on conservait les nombres dans la main gauche, et à partir de cent, le total était reporté dans la main droite.

 

«C'est bien lui le berger qui laissa derrière les quatre-vingt-dix-neuf brebis qui ne s'étaient pas égarées et vint chercher celle qui s'était égarée. Il fut plein de joie, lorsqu'il la trouva. Car 99 est un nombre qui est compris dans la main gauche. En revanche, une fois que l'on a trouvé le « un », le nombre entier est transféré à droite. De même, c'est ce qui est privé du « un », c'est à dire la main droite toute entière, qui attire ce qui manque, et le prend du côté gauche pour le faire passer à droite, et ainsi le nombre devient cent. Tel est le symbole de ce qui se trouve sous la prononciation de ces nombres. Tel est le Père : même pendant le sabbat, la brebis qu'il a trouvée tombée dans le fossé, il peine pour elle. Il garde en vie la brebis, une fois qu'il l'a rencontrée dans le fossé

Veillez à comprendre spirituellement – vous les fils de la compréhension spirituelle - ce qu'est le sabbat ; c'est le jour où il ne convient pas que le salut soit inactif. »

 

Nous aurons à nous souvenir de cette dernière phrase dans la seconde partie de cette étude.

Nous voyons que la doctrine de l'Evangile de vérité attribue au nombre 99 une fonction de pivot ou de bascule qui, toutefois, ne sollicite aucune des propriétés mathématiques que nous lui avons associées précédemment, mais seulement son statut ordinal de prédécesseur du nombre cent, qui fait de lui un nombre qui en « appelle », ou en attire un autre, sur la base d'un manque, d'une incomplétude intrinsèque.

Nous verrons dans la prochaine remarque que la tradition pythagoricienne a effectué une synthèse harmonieuse entre les deux aspects du nombre 99 que nous venons de développer séparément.

 

Il n'est pas besoin d'être expert en théologie pour saisir que ce passage est une exégèse sophistiquée de l'axiome évangélique « les derniers seront les premiers », qui associe ce précepte, d'une part, à la doctrine du sabat, d'autre part, à une forme de symbolisme arithmétique, inspiré du comput digital. Selon Aliboron. cet évangile développe une véritable théologie du Nom, fondée sur l'axiome : Le Nom du Père est le Fils. « Le caractère improférable du Nom, décliné à l’envi dans cette doctrine gnostique, souligne la nature cachée de Dieu. Car par l’épithète d’AMEN (le Fidèle, le Véritable) qui lui est attribué dans l’Apocalypse, le Christ, selon les spéculations sur la valeur numérique des lettres grecques, s’apparente au nombre 99 (A+M+H+N = 1+40+8+50 = 99) ; il peut donc être « enfermé » dans les cinq doigts de la main gauche. Pentagramme qui le met en relation avec Sirius, et lui confère un statut de médiateur de vérité : voie d’accès obligée vers le 100eme nom, celui du « Caché », Amon. « Car nul ne vient au Père que par moi » affirme Jésus (Jean, 14,6). » (Aliboron)

 

 

 

22. LA TRADITION PYTHAGORICIENNE SYNTHETISE TOUTES LES IDEES FORMULEES DANS LES REMARQUES PRECEDENTES PAR UNE STRUCTURE PENTAGRAMMATIQUE

 

 

Un pentagramme connu dans la tradition pythagoricienne, et notamment utilisé par André Charpentier, organise l'ensemble des multiples de 9 inférieurs à cent, dont le dernier élément, le nombre 99 - qui marque, comme on sait, la « rencontre » de cette famille avec celle des palindromes - joue le rôle de centre de symétrie général de la structure.

 

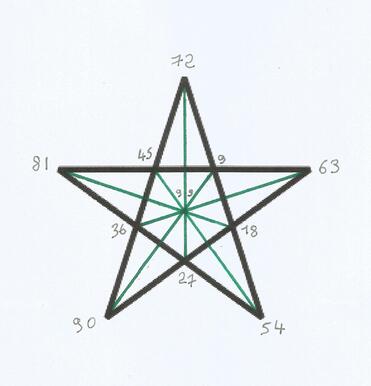
En effet, dans cette structure, chaque nombre est associé, ici par un segment vert, à un nombre polaire, avec lequel il forme un palindrome, et qui, additionné à lui, produit le total de 99. Le nombre du centre, n'ayant pas de correspond polaire, demeure naturellement invariant.

Le nombre 11 n'est présent dans cette figure, comme il est naturel, que de manière structurale : il quantifie les barreaux de l'escalier ordinal qui va de 9 à 99, barreaux qui sont les 11 points de la structure.

Il n'est pas difficile de voir que la logique de ce pentagramme se répercute à des niveaux arithmétiques supérieurs. En effet, aux valeurs de ce premier pentagramme, on peut appliquer la fonction de duplirotation qui permet d'engendrer « une famille plus spacieuse » de multiples de 9.

Le nombre 99 – on ne l'aura pas oublié – est le premier membre d'une classe de nombres qui sont à la fois multiples de 9 et de 11, et qui réunissent donc les propriétés des fonctions anagramme et palindrome.

Notre second pentagramme s'intéresse à cette famille, dont le nombre 99 est le premier représentant, et recense tous les nombres de cette famille inférieurs à 10 000 qui sont des palindromes stricts. Il y en a à nouveau 11, et ils s'organisent autour d'un centre qui est, cette fois, le nombre 9999

Il n'existe que 11 nombres inférieurs à 10 000 qui soient à la fois multiples de 9 et de 11, et palindromes stricts

1. 99 x 1 = 99

2. 99 x 19 = 1881

3. 99 x 28 = 2772

4. 99 x 37 = 3663

5. 99 x 46 = 4554

6. 99 x 55 = 5445............................. milieu de la série

7. 99 x 64 = 6336

8. 99 x 73 = 7227

9. 99 x 82 = 8118

10. 99 x 91 = 9009

11. 99 x 101 = 9999

 

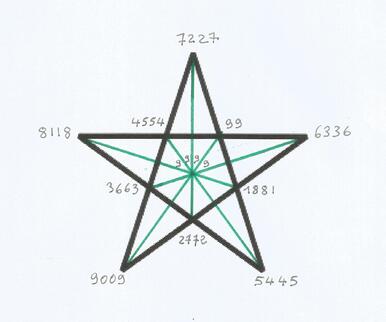
Nous voyons que les pentagrammes pythagoriciens synthétisent l'ensemble des idées développées dans les remarques précédentes. D'une part, ils développent le rapport dialectique intime qui rattache les nombres anagrammes aux nombres palindromes, d'autre part, chaque pentagramme se place sous le signe d'un seuil, d'un plafond théorique, qui est, pour le premier, le nombre 100, et pour le second, le nombre 10 000

Le lecteur attentif aura remarqué une singularité dans ce second pentagramme : le 99 ne semble pas répondre polairement à 9009, puisque leur addition ne donne pas 9999. En réalité, la logique de ce pentagramme s'applique un système à 4 termes, où les palindromes sont construits par duplirotation de leur moitié, de sorte que le nombre 99 occupe ici en réalité, non pas les deux dernières places de la formule à 4 termes, mais les deux places du milieu. Une fois compris ceci, on s'aperçoit qu'il n'y a pas d'anomalie dans le pentagramme, simplement, le 99 vient remplacer les deux zéros qui sont au milieu du nombre 9009, pour former régulièrement le nombre 9999. De sorte que le 99 initial doit être conçu comme précédé et suivi d'un zéro « positionnel », et par là même adopter la valeur arithmétique du nombre 990 - alors même que ce nombre, n'étant pas un palindrome strict, n'a pas sa place dans la logique restrictive du pentagramme.

0990

9009

Les chiffres des deux formules s'additionnent verticalement pour former le nombre 9999

 

Du fait de se situer sous le « plafond de verre » des nombres 100 et 10 000, respectivement, les deux pentagrammes se cantonnent dans une « main gauche », dans un statut d'incomplétude et de manque qui « appelle » ou « attire » un état plus complet, symbolisé par ce plafond.

 

Une fois ces présentations faites avec les propriétés du nombre 99, le lecteur va enfin découvrir en quoi elles concernent la nef !

 

 

 

23.EN AFFECTANT LE TRIANGLE AURIGENE D'UN FACTEUR 33, ANDRE CHARPENTIER A SOUMIS LES COTES DE CE TRIANGLE A UN PRINCIPE DE COMMENSURABILITE GENERALE SOUS L'EGIDE DU NOMBRE 99, ET MIS EN LUMIERE UNE PROPRIETE NUMEROLOGIQUE DE LA RELATION DE PYTHAGORE, ENTRE LES CATHETES ET L'HYPOTENUSE DU TRIANGLE.

 

 

Les travaux d'André Charpentier ont montré l'importance du triangle aurigène (1, 2, rac5) pour une compréhension pleinement pythagoricienne de la doctrine du nombre d'or.

Charpentier affecte les côtés du triangle aurigène d'un facteur 33 et obtient la figure suivante.

 

 

Comme il se doit, les valeurs des côtés du triangle prennent place dans une expression qui définit le nombre d'or :

Φ = (√ 5445 + 33) / 66

On remarque que la forme palindrome du nombre 33 se répercute, non seulement sur la cathète voisine, mais aussi sur l'hypoténuse, pourtant irrationnelle.

La valeur de cette hypoténuse n'est pas une inconnue pour nous, puisque nous l'avons rencontrée dans le second pentagramme pythagoricien, où le nombre 5445 occupe, dans la série des palindromes multiples de 9 et de 11 inférieurs à 10 000, le sixième rang, c'est-à-dire la position du milieu.

Le théorème de Pythagore exprime une relation entre les cathètes et l'hypoténuse du triangle rectangle qui, en toute justesse, ne concerne que le développement carré de ces grandeurs : le carré de l'hypoténuse est égal à la somme des carrés des cathètes. Mais il est possible de se placer, par imagination, sur un plan hypothétique plus général, selon lequel le développement carré ne serait qu'un aspect de la relation entre ces objets. Autrement dit, il pourrait exister d'autres situations mathématiques dans lesquelles « les cathètes se reflètent dans l'hypoténuse », qui ne concerne pas spécifiquement le développement carré de ces grandeurs, mais d'autres propriétés de ces grandeurs.

C'est précisément une propriété de ce genre que met en lumière l'équation de Charpentier.

On observe en effet que

33 + 66 = 99

tandis que

54 + 45 = 99

Autrement dit : la somme des valeurs des cathètes est égale à la somme des parties du palindrome de l'hypoténuse.

Au lieu que le théorème classique est un théorème de "développement" (construction de carrés sur les côtés du triangle rectangle) celui-ci est un théorème de "résorption" ou d'involution.

L'équation de Charpentier met en jeu 3 différentes propriétés des nombres.

A. La propriété "palindrome" propre aux nombres 33, 66, 5445

B. Les propriétés additives des multiples de 9

C. La propriété synthétique qui, dans le cas du nombre 5445, réunit les propriétés A et B

En actionnant ces propriétés naturelles du nombre, Charpentier ne fait que répondre à l'appel de la symétrie. Le nombre 99 occupe, dans l'équation de Charpentier, la fonction qu'occupe le nombre 5 dans le « développement carré » du triangle aurigène, et la relation classique de Pythagore où les carrés des cathètes (1+4) se reflètent dans le carré de l'hypoténuse (5)

Le nombre 99 étant multiple de 33, il est possible , naturellement, de transformer l'équation de charpentier sur le nombre d'or en une formule qui fasse « ressortir » partout le nombre 99.

Φ = (√(99 × 55) + (99 ÷ 3)) ÷ ((99 ÷ 3) × 2)

Le nombre 99 joue alors, pour les côtés du triangle aurigène, le rôle de commune mesure, de principe de commensurabilité – et donc un rôle essentiellement analogue à celui joué par le petit segment de valeur 1 qui parcourt les côtés du triangle isiaque.

 

Une célèbre équation de Ramanujan met en jeu le nombre 99 dans la définition du nombre π. Tout ce que nous pouvons en dire est qu'elle fait intervenir des nombres qui, en mathématique pythagoricienne, correspondent à des individualités géométriques, comme, au numérateur, le carré de 99 (9801 = 99²), et au dénominateur, le nombre 396 (= 4 x 99). Mais nous ignorons, en toute bonne foi, s'il y a un sens à l'engager dans une comparaison avec l'équation de Charpentier sur le nombre Φ.

 

 

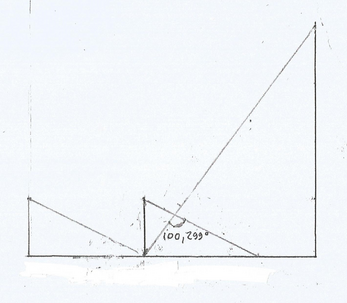
On pourra également relever, comme une curiosité, l'angle que forment entre elles les hypoténuses racine 5 et 5, lorsque le triangle aurigène pénètre dans le triangle isiaque : 100,299°

 

 

 

 

24. LA FORMULE DE CHARPENTIER SE DECLINE EN DIVERSES VARIANTES PALINDROMIQUES, ET SE RESOUT TETRACTYQUEMENT

 

 

Détaillons les propriétés de l'équation de Charpentier :

 

Côtés du triangle                      Carrés adjacents aux côtés              Division des carrés par 99  

33                                                  1089                                                       1089/99   =   11  

66                                                  4356                                                       4356/99   =   44    

racine 5445                                   5445                                                        5445/99   =   55

 

On peut déjà en déduire une première transformation de l'équation, dans laquelle l'unité commune aux trois côtés n'est plus le nombre 99, mais le nombre 11, principe des nombres palindromes :

Φ = ((√55) + (√11)) / (√44)

Et on observe cette propriété des carrés adjacents, bien que seul le troisième soit palindrome.

1089              10+89             = 99

4356              43+56             = 99

5445              54+45             = 99

Propriété qui se présente sous la forme d'un complexe naturel.

Si nous reprenons l'équation :

Φ = ((√11) + (√55)) / (√44)

Celle-ci peut à son tour être transformée en quelques étapes, jusqu'à retrouver la forme tétractyque

 

Φ =     √(11)  + √(11+11+11+11+11)  

                 √(11+11+11+11)

 

Φ =       √(11) + √((11+11) + (11+11+11))
                 √(11+11+11+11)

 

Φ =       √(1) + √((1+1) + (1+1+1))
                 √(1+1+1+1)

 

 Φ = ( √1 )+ √(2+3 ) 

                  √4

 

Pour le plaisir des pythagoriciens, il est possible de clore ce processus de simplification par un dessin, dans lequel les parties de la tétractys sont associées aux côtés du triangle aurigène qui leur correspondent. On remarquera que le sommet de la tétractys et la 4ème ligne correspondent aux côtés de l'angle droit, et la partie médiane à l'hypoténuse, ce qui est ajusté à la fonction médiante, "moyennante" que Charpentier prête à l'hypoténuse.

 

 

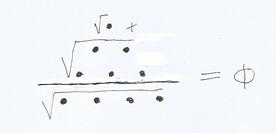
Le rapport doré peut alors apparaître comme une modalité du rapport cosmologique 3/2, du rapport de quinte qui, dans la tétractys, met en relation les 3 premiers étages avec le quatrième, mais aussi, les points de l'hexagone avec ceux du trépied ; rapport que l'on retrouve dans les nombres principes des jambes du Lambda, comme dans la construction d'un pentagone à partir de la division d'un cercle selon ce même ratio 3/2. Il n'y a véritablement dans ces structures qu'un seul et même logos pythagoricien.

 

 

25. LA SCENE PRIMTIVE DU TRIANGLE ISIAQUE EST EQUILIBREE PAR LE NOMBRE 9

 

 

Le triangle 3,4,5 possède, dans la série des triplets, le statut de principe qui est celui du nombre 1 dans la série des entiers. Pour les anciens, ce triangle semble avoir représenté quelque chose comme la « scène primitive » du théorème de Pythagore ; et la mathématique moderne a confirmé ce préjugé, en remarquant que ce triangle était doté de propriétés uniques, ne réapparaissant dans un aucun des triplets de la suite.

En premier lieu, le triangle isiaque est un exemple d'application restrictive du théorème de Pythagore, qui conduit à définir une classe d'objets. Cette classe, nomenclaturée par les triplets, est celle des carrés entiers qui sont la somme de deux carrés entiers.

Mais de la même manière qu'on peut, sur les côtés d'un triangle, développer des carrés, on peut aussi développer des cubes. Or, si l'on développe les cubes adjacents aux côtés du triangle isiaque, on s'aperçoit que la somme de ces cubes est égale à un autre cube, qui n'est autre leur successeur dans la série des cubes.

 

 

3³ + 4³ + 5³ = 6³

En résumé : sous le rapport du développement carré, le triangle isiaque se rapporte à la série des « carrés qui sont la somme de 2 carrés » - série dont le triplet isiaque est le premier représentant ; tandis que, sous le rapport du développement cubique, le triangle isiaque se rapporte à la série des « cubes qui sont la somme la somme de 3 cubes » - série dont le quadruplet isiaque est à nouveau le premier représentant.

Remarquons que la quantité d'objets impliqués dans chaque équation est proportionnelle à la dimension dans laquelle l'opération s'effectue. On additionne 2 carrés en dimension 2, mais 3 cubes en dimension 3

Au sein de la série des cubes qui sont la somme de trois cubes, le quadruplet isiaque possède une propriété unique, que ne peut posséder aucun autre des quadruplets premiers de la suite : ses éléments sont en médiété arithmétique. En effet, il est aisé de démontrer que, si, dans la suite des cubes qui sont la somme de trois cubes, un quadruplet est en médiété arithmétique, alors, ce quadruplet est un k-multiple du quadruplet isiaque.

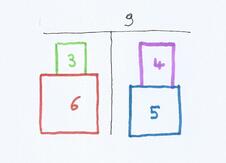
Cette propriété unique a pour conséquence que le quadruplet isiaque possède un « nombre d'équilibre », que l'on obtient en faisant l'addition de ses extrêmes, et celle des termes du milieu :

3+6 = 9

4+5 = 9

Nous pouvons vérifier géométriquement cette situation d'équilibre en empilant le petit cube sur le gros, et le deuxième sur le troisième, les deux tours étant équilibrées par une toise de hauteur 9

 

Si la proportion arithmétique est donc un privilège unique du quadruplet isiaque et de ses k-multiples, il est néanmoins possible d'abstraire, de cette proportion arithmétique, des propriétés de symétrie moins fortes que pourraient, par hypothèse, posséder d'autres quadruplets que le quadruplet isiaque.

Ainsi, on peut appeler, par exemple, « quadruplets équilibrés » les quadruplets dans lesquels, sans qu'ils soient forcément en proportion arithmétique, on a la relation a+d = b+c

Dans le même esprit, on pourra appeler « quadruplets doublement équilibrés » une famille plus étroite de quadruplets qui (toujours sans être nécessairement en proportion arithmétique), présenteraient non seulement la relation :

a+d = b+c

mais en outre la relation :

b-a = d-c

Nous donnons ci-dessous une liste des cent premiers cubes qui sont la somme de trois cubes. Notre quadruplet isiaque est le premier. Une fois supprimés ceux qui ne sont pas premiers (ce que nous avons fait en les surlignant en couleurs), il en reste un peu moins de la moitié. On sera peut-être surpris de remarquer que d'assez nombreuses formules de décomposition coexistent, parfois, pour un même nombre.

 

On remarque dans cette liste, qu'en dehors du quadruplet isiaque, aucun autre quadruplet premier n'appartient ni à la classe des quadruplets « équilibrés », ni par conséquent encore moins, à celle des quadruplets « doublement équilibrés », - bien que ces conditions de symétrie soient moins fortes que celles imposées par la proportion arithmétique.

En effet, les seules formules qui appartiennent à ces deux classes sont les formules barrées en rouge qui correspondent aux k-multiples du quadruplet isiaque, et ne sont donc pas des quadruplets premiers.

Ces remarques pourraient être traduites par un proverbe du genre : loin de l'origine, point d'harmonie !

Au sujet de ces formules surlignées en rouge, qui sont les k-multiples du système isiaque, on pourra remarquer, à présent, qu'en empilant un système k=1 (notre système isiaque) sur un système k=10, on obtient, comme il se doit, une tour de la même hauteur que le système k=11, les deux tours étant équilibrées par une toise de hauteur 99

 

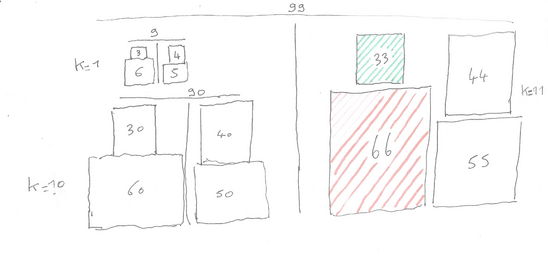
Quant à ce système k=11, de hauteur 99, (qui, rappelons-le, n'est rien d'autre que le développement arithmétique d'ordre 11 de la scène primitive du triangle isiaque), il ne sera pas sans nous rappeler, sans doute, les manipulations palindromiques d'André Charpentier sur le triangle aurigène, puisque les faces des cubes de sa première tour (d'arêtes 33 et 66), ne sont pas différentes des carrés des cathètes du triangle aurigène de Charpentier, donnant lieu à sa première équation du nombre d'or

Φ = (√ 5445 + 33) / 66

 

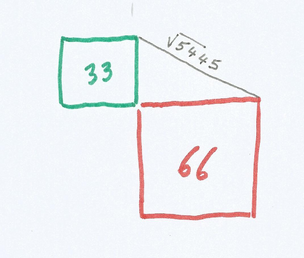
Tandis que les valeurs de la seconde tour (44, 55) nous sont pas inconnues non plus, puisqu'elles apparaissent, sous la forme de racines carrées, dans une autre définition du nombre d'or, dérivée de la précédente.

Φ = ((√55) + (√11)) / (√44)

Prenons le temps de récapituler le chemin accompli sous l'égide du nombre 99.

En soumettant, d'une part, le triangle aurigène à un principe de développement involutif, et d'autre part, le triangle isiaque à un principe de développement gnomonique et croissanciel, le nombre 99, et la fonction palindrome, conduisent la logique de ces deux triangles à se rejoindre.

Du côté aurigène, le nombre 99 apparaît comme un quantum d'involution du rapport des côtés du triangle, permettant qu'apparaisse un rapport entre « la somme des cathètes » et « les parties du nombre » de l'hypoténuse ; tandis que, du côté isiaque, les nombres 33 et 66 (mais aussi 44 et 55) qui gouvernent le rapport doré, apparaissent comme l'horizon du développement gnomonique du triangle (système k=11)

La logique des deux systèmes se rejoint donc à leur horizon respectif, d'involution réflexive pour le premier, de développement gnomonique pour le second.

 

 

26. LE NOMBRE 216 QUI, DANS LA TRADITION PYTHAGORICIENNE, CORRESPOND A L'INTERSECTION ENTRE LE PRINCIPE DE L'AME DU MONDE, ET CELUI DES INCARNATIONS DIVINES ET HUMAINES, EST AUSSI UN OPERATEUR DOTE DE DIVERSES FONCTIONS HORLOGERES

 

 

Relativement au développement gnomonique tridimensionnel du triangle isiaque 3-4-5, le nombre 216 (=6x6x6) joue le rôle de principe englobant, ou enveloppant.

Par sa fonction géométrique, comme par sa forme hexagonale, ce nombre exprime la cyclicité, la complétude, le retour du Même.

Ce nombre est bien connu de la tradition ésotérique pythagoricienne, puisqu'il correspond au cycle des réincarnations de Pythagore, ou du moins au demi-cycle.

La situation exceptionnelle de ce nombre s'explique par le fait qu'il est l'intersection de deux processus, d'une égale importance, et qui ont tous deux laissé des empreintes dans l'oeuvre de Platon, le premier dans le Timée, le second dans La République, comme on le verra dans la seconde partie de cette étude ; - situation que l'on peut représenter à l'aide d'un Lambda.

 

                            216 (3³+4³+5³)

            108                            50 (3² + 4² + 5²)

54                                                     12 (3 + 4 + 5)

 

Jambe gauche, le nombre 216 prolonge la série des nombres vitaux impliqués dans l'harmonie musicale et dans la construction de l'âme du monde ; jambe droite, il correspond au développement complet du triangle isiaque, du segment à la surface, et de la surface au volume.

La jambe gauche correspond au principe de l'animation, de l'harmonie vibratoire et de la durée du monde. La jambe droite, au principe de la condition spatio-temporelle de l'être incarné, au sens du développement complet, pour une individualité quelconque, qu'elle soit divine, humaine, ou même, comme Pythagore, quelque chose d'intermédiaire, d'un nombre limité de possibilités, défini par les « constituants » ou les prémisses qui la fondent.

De cette manière, il semble envelopper à la fois le principe de la vie du monde, et celui des êtres qui naissent en son sein, soumis à une même condition spatio-temporelle.

Du point de vue astronomique, le nombre 216 est souvent impliqué – comme on aura l'occasion d'y revenir aussi - dans le cycle de la précession des équinoxes, qui joue un rôle central dans de nombreux calendriers traditionnels, babyloniens, indiens ou chinois, et intervient souvent dans le calcul de la « grande année ».

Mais, relativement à un tel cycle, le nombre 216, associé à la manifestation de l'âme et de la vie incarnée, relève d'une dimension en quelque sorte « transcendante ».

En effet, le nombres de la jambe droite ne doivent pas être compris comme assujettis à ceux de la jambe gauche, comme le serait la condition d'un être « contenu », relativement à celle d'un être « contenant ». Car en effet, le monde lui-même peut être conçu comme une réalité soumise à la condition « incarnatoire » ; et donc la relation entre les deux branches doit bien plutôt être comprise comme une relation de sujétion mutuelle.

En tant que nombre de Pythagore, multiple de 6 et de 12, et donc, nombre cyclique ou circulaire, le nombre 216 a un aspect nettement « solaire ».

Néanmoins, c'est bien le nombre 9 qui joue le rôle le plus important dans l'exégèse symbolique de ce nombre, puisqu'il est déterminant de part et d'autre de la procession figurée par notre lambda.

Jambe gauche, le nombre 216 correspond au développement d'une famille « octavique », comprise de bout en bout dans l'ensemble des multiples de 9 ; jambe droite, on se rappelle que le nombre 9 est le principe d'équilibre qui régit, non seulement le développement du triangle isiaque, mais aussi celui du triangle aurigène, dans lequel les mêmes nombres se déploient, avec des fonctionnalités différentes.

Enfin, la division de 216 par 9 donne 24, ce qui suggère la possibilité d'une projection analogique, endomorphique, entre la « l'année incarnatoire » (ou plutôt son semestre) régissant les vies de Pythagore, et le cycle de la journée terrestre.

 

La séquence qui suit offre un raccourci du chemin accompli dans ce chapitre 4 ; elle méritera que l'on s'en souvienne lorsque nous aurons, dans la conclusion de cette étude, à traiter de la grande tétractys 36

 

1³ + 2³ + 3³ =   6 x   6 =     36

 2³ + 3³ + 4³ = 11 x   9 =     99

 3³ + 4³ + 5³ = 12 x 18 =   216

 

Cet ensemble d'équation peut être rapproché de deux autres, plus familières peut-être, du fait qu'elles se rapportent à des divisions habituelles du temps

 

3x4x5 = 60/1 = seconde/minute = minute/heure

3x4x5x6 = 360/1 = jour/année (par une approximation certes grossière, mais traditionnelle)

 

Ces rapports arithmétiques ont eu pour conséquence particulière que, dans diverses traditions, le nombre 216 peut – rétrospectivement - être investi d'une fonction purement horlogère. Quelques exemples :

Il y a 216 x 5 halakim hébraïques dans une heure.

Il y a 216 x 50 muhurtas indiens dans une année de 360 jours

Des équivalences du même acabit pourraient enrichir cette recension traditionnelle, telles que :

Il y a 216 neuvièmes d'heures dans une journée.

On notera que, dans ces exemples, le nombre 216 se rapporte aux divisions habituelles du temps par la médiation des nombres 5 et 9

Mais on peut encore remarquer, comme le fait d'Arcy Thompson, qu'il y a

216 x 240 000 minutes dans un siècle - où le 240 000 fait écho, à nouveau, à la division en 24 des heures d'une journée.

 

Du côté du 99, Charpentier se réfère à plusieurs reprises, sans citer ses sources, à une tradition selon laquelle l'année pythagoricienne compterait 99 mois

Il s'agit là probablement, cette fois, d'un calendrier luni-solaire. Avec une lunaison de 29,5 jours et une année de 365,25 jours, on a 12 lunaisons = 354 jours, et 1 année = 12 lunaisons + 1 reste de 11,25 jours En regroupant 8 années solaires, on monte à 96 lunaisons + 1 reste de 88,75 jours, reste qui est très proche de 3 lunaisons. Autrement dit 8 années = 99 lunes ; mais on ne fait finalement que retrouver ainsi le cycle dit octaétérique du calendrier attique, dans lequel les 99 mois lunaires se répartissent dans une "grande année" terri-solaire de forme « octogonale ».

 

 

 

27. L'HERMETISME ET LA CABALE ONT EXPLOITE LES PROPRIETES MAGIQUES ET GUEMATRIQUES DU NOMBRE 216, DE CONCERT AVEC SES PROPRIETES MATHEMATIQUES

 

 

Pour commencer, plaçons sous les yeux du lecteur ce dessin qui décompose les cubes de la cité isiaque en éléments tels que plaques, bâtonnets, ou petits cubes atomiques, de manière que chaque cube puisse être considéré comme le noyau du cube de rang supérieur, au moyen d'un complément en forme de « coin ».

 

 

Sur le plan mathématique, on a cette relation entre la somme des cubes et le carré des nombres triangulaires :

On peut imaginer que l'exposant 3 s'inscrit dans une suite :

• 3^0

• 3^1 , 4^1

• 3^2 + 4^2 = 5^2

• 3^3 + 4^3 + 5^3 = 6^3

Cette présentation fait émerger les relations « carré » et « cube » aux rangs même où, dans la tétractys, émergent les dimensions 2 et 3

Evidemment, le processus ne « produit pas d'équation » avant le troisième rang. Ce qu'on peut éventuellement gloser en disant que l'équilibre ne peut surgir avant le troisième pas. Le second pas discrimine, ce n'est qu'ensuite qu'émerge la balance.

Le fait que ce déploiement commence avec le nombre 3 peut se comprendre en terme de cosmogenèse ; si celle-ci commence avec le sacrifice de la hiérarchie des Trônes — qui est la 3ème hiérarchie correspondant à la sphère de Saturne (comme son indice de carré magique), alors l'équation cubique correspond au développement proprement terrestre du globe, initié par la création des Elohim solaires (6ème hiérarchie).

 

Sur un plan plus kabbalistique, on peut noter que la cinquième sephira Geburah vaut 216 ; et précisément, un kabbaliste chrétien (Knorr von Rosenroth) avait créé un nouveau carré magique de 6 — associé donc à la sephira suivante — de constante magique 216, au lieu du traditionnel 111.

Outre le "recentrage" chrétien sur le 666, il y a comme une passerelle (intentionnelle) entre le 5 et le 6, qui pourrait évoquer le « noyau quinaire » du cube de 6, et dont on pourrait dire, qu'elle évoque aussi le "concept commun de puissance" entre les Vigueurs martiennes (5) et la Force solaire (6).

L'équation 1^3 + 2^3 + 3^3 + 4^3 + 5^3 = (1 + ... + 5)^2

devient : (1 + 2)^2 + 216 = 15^2

ou encore 216 = 15^2 — 3^2

Autrement dit, 216 est la différence entre deux carrés, DONC une somme de gnomons, et précisément de 12 nombres impairs consécutifs.

216 = 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29

Une autre manière duodécimale d'interpréter le 216 est simplement :

216 = (3^2) x 3 + (4^2) x 4 + (5^2) x 5

C'est à dire une somme de 12 carrés.

Qui se recombinent d'ailleurs en

216 = (7+9+11) + (13+15+17+19) + (21+23+25+27+29)

La présence du 12 est intéressante, puisque c'est à la fois 3+4+5, et en lien avec la dimension 3 via Barazzetti.

Au passage, les nombres médians 17 et 19, nombres premiers jumeaux, sont tels que 107 + 109 = 216 avec 107 et 109 nombres premiers jumeaux.

 

Symboliquement, on a 12 équerres qui "s'appuient" sur le carré de Saturne.

Ou peut être mieux, en couplant les équerres en rectangle, on a 6 rectangles gigognes — de périmètre 216 = 16 + 24 + 32 + 40 + 48 + 56 — enserrant le carré de Saturne. 

De quoi aller jusqu'à la Terre.

 

Le 216 apparaît donc comme le reste d'un "évidage" de 1 rectangle sur 7 rectangles (car le carré de Saturne n'est jamais que UN rectangle pointé).

En définitive, on est là dans le domaine des "nombres octogonaux centrés" :  1, 9, 25, 49, 81, 121, 169, 225.

 

Où 225 est bien le 7ème du genre, sans compter le 1 qui n'est pas vraiment rectangulaire.

Par ce retranchement désormais recentré en dénoyautage, on rejoint l'idée radicale de "troncature", dans la mesure où son étymon a donné le grec sarx = la chair, la pulpe. Avec ses sous-entendus "terrestres" (Et le verbe s'est fait chair : Καὶ ὁ λόγος σὰρξ ἐγένετο).

Plus encore, on pourrait comprendre cette descente du Christ en polarité du tsimtsoum : le Père se contracte en un point, laissant un espace vide alentour ; mais le Fils remplit cet espace vide, en s'élançant, en quittant "son Trône". 

 216 serait la signature de ce remplissage. Par sa fonction rédemptrice, tikkunique, il se voit "proportionné" au 666.

Dans la liste des quadruplets,on trouve un « multiple double » du nôtre : 6, 8, 10, 12 — dont la constante vaut 1728, soit 2^3 fois 216

Le suivant, de constante 5832 est à la confluence de notre quadruplet (multiple de 3) et du suivant (multiple de deux de la suite 1, 6, 8, 9)

Ce quadruplet 1, 6, 8, 9, est, du reste, remarquable en ce qu'il est le seul à faire intervenir le cube de 1

 

*

 

On a vu qu'une équerre volumique se recombinait en « gros cube » + un « coin »

Ce gros cube est géométriquement de la forme : 3 fois un nombre oblong.

Soit l’équation x^3 = 3y(y+1)

Dans notre cas : 3 fois (8 x 9) = 216 = 6^3

Mais sur un plan symbolique, on peut quand même relever que 6 est le premier oblong « vrai » au sens où 2 et 3 sont des « nombres » au sens fort. A ce titre, il est le double du premier nombre triangulaire « vrai » = 3.

Il y a un jeu « hiérogamique » d’écriture.

3 fois (2^3 . 3^2) = (2.3)^3

 

 

En hébreu, la lumière = AWR

 aleph = 1, waw = 6, reish = 200

 qu'on peut lire, dans une guématrie décimale, 162

 valeur approchée de phi.

 *

 

 

 

 

 Du point de vue cosmologique, le triangle aurigène représente la fonction du centre, et le principe animateur, ou activateur qui permet à l'Un d'engendrer le Multiple sans sortir de soi-même, par un simple contact interne, une électrisation, tandis que le triangle isiaque, gouverné par le logos d'octave , représente le champ, le plan récepteur de cette action électrisante : le principe passif de la manifestation universelle, qui n'est autre que sa condition, sa constitution spatio-temporelle. 

Ces deux principes pourraient, au premier abord, être assimilés aux principes masculin et féminin que l'on a déjà vus, chez maints commentateurs, associés au jambes du lambda de Platon ; mais il convient de considérer qu'on est ici au cœur d'une hiérogamie, dans laquelle le féminin et le masculin entrent en composition, dans une harmonie qui les enroule autour de l'Un, dont ils procèdent.

En tant qu'ils se rapportent, pour le premier, au rapport doré, et pour le second au rapport d'octave, nos triangles apparaissent aussi comme les symboles des deux coups de couteau originaires de la création, de la même manière que, dans la vesica piscis, le premier cercle est contraint de s'en adjoindre un second; et donc la création d'émerger depuis deux foyers. Ce qui rejoint aussi les intuitions de Charpentier sur le rayon céleste 99.

 

Nos études futures nous permettrons d'associer à ces principes, de façon plus assurée, des fonctions à la fois plus précises et plus universelles, relevant de la cosmologie.