-
Bloc-notes
BLOC-NOTES
de Rémy BAYOUD
Chère Maryvonne,
Ali vient de nous livrer une petite étude tout à fait intéressante, et qui devrait te plaire. A noter cette idée d'invariance...
Je ne sais pas si je t'avais parlé du folkloriste Philippe Walter, mais il donne beaucoup d'indications calendaires. Il relève notamment l'apparition périodique, tous les quarante jours, d'un géant dans les rites annuels pré-chrétiens. Ce genre de période m'intéresse pas mal. Elle m'étonne aussi dans la mesure où le calendrier compte les mois "avec la lune", contrairement par exemple aux Aztèques qui divisaient l'année en mois de 20 jours. Reste que les Celtes semblent avoir utilisé (au moins en partie) une numération vigésimale, dont la langue française garde quelques traces. Lu également, que l'alphabet oghamique, probablement druidique, composé originellement de 20 caractères, aurait dérivé d'un système de 10 lettres-doubles.
Il me semble qu'on peut imaginer ce genre de division de l'année, où les ---- représentent une période fixe de 40 jours, et --- recouvre la période de 30 jours de Canicule. Les deux sauts de ligne représentent des intervalles variables (comput lié à la lune) mais dont la somme vaut environ 50 jours.
St Martin (11 nov) ---- Sol Invictus ---- ChandeleurMardi-Gras ---- Pâques ---- Ascension
St-Jean ---- Début de Canicule (Lion astrologique) --- Fin de Canicule ---- St Michel (29 septembre)
Soit (à peu près) : 30 + 7 x 40 + 50 = 360Avec 8 temps forts (rose des vents) répartis autour des 4 grandes fêtes (sinusoïdales) + 4 points remarquables (solstices et équinoxes) co-sinusoïdaux, c'est à dire en quadrature de phase. Car parmi les 10 temps précédents, la Canicule est dédoublée, et d'une manière un peu différente Chandeleur et Mardi-Gras.
*
De mon côté, je viens de prendre connaissance d'une étrange métrologie, baptisée "géométrie mégalithique" : fondamentalement elle énonce une division du cercle en 366 degrés. Ce qui expliquerait certains alignement géographiques des anciennes cités, et permettrait de retrouver un étalon appelé "yard mégalithique" (0,8296 m) utilisé dans les constructions anciennes.
Butler et Knight affirment que le yard mégalithique est un nombre fondamental du soleil, de la lune et de la terre : en effet, la seconde d'arc mégalithique mesurée à l'équateur terrestre mesure près de 366 yards mégalithiques [note de Rémy : c'est en divisant les 40 000 km de la circonférence terrestre par 366 qu'on retrouve le yard] la seconde d'arc lunaire mesurée à l'équateur lunaire mesure près de 100 yards mégalithiques, et la seconde d'arc solaire mesurée à l'équateur solaire mesure près de 40 000 yards mégalithiques.
Dans un ouvrage paru en 2007, l'auteur français Sylvain Tristan affirme que les nombres 366, 40 et 10 sont non seulement fondamentaux à ces trois astres, mais également au corps humain et à l'eau : dans le système de mesure des températures Celsius, fondé sur l'eau et directement lié à la base 10, la température du corps humain est en moyenne de 36,6 degrés (d'après la médecine russe qui considère la température mesurée sous l'aisselle), et la température de densité maximale de l'eau serait de 4,0 °C (elle est en fait de 3,98 °C)
En dehors de ces informations, que je suppose pour le moment factuelles, l'idée peut paraître étrange de privilégier un tel nombre, face au "champion" 360. C'est alors que je me suis souvenu que Plutarque aurait écrit dans le Silence des Oracles :
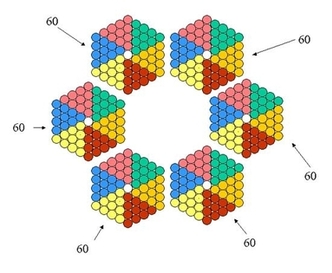
"Pythagore disait que ni le nombre des mondes n'est infini, ni qu'il n'y en avait pas un seul, ni cinq, mais cent quatre vingt trois ; qui étaient ordonnés et rangés en forme triangulaire, duquel triangle chaque côté contenait soixante mondes, et que des autres trois, chacun était à l'un des côtés du triangle, et qu'ils s'entretenaient tout à l'entour ni plus ni moins que ceux qui sont en une danse, et que la plaine qui est au-dedans du triangle, était le fondement et l'autel commun de tous ces mondes, qui s'appelait le champ ou la PLAINE DE VERITE, etc..."
M'as-tu déjà parlé de ce nombre ? Je n'en ai pas souvenir. Dom Neroman vient à mon secours, avec son concept de "roues magiques", que j'expose seulement dans les grandes lignes. Il s'agit de roues de nombres "générées" par un nombre premier, qui ont selon les cas certaines propriétés spéciales. Par exemple, la roue-60 générée par l'insécable G=61, ou la roue-108 par G=109. La construction de cet auteur consiste à insérer les roues (1 - 60) & (1+G - 60+G) & (1 + 2G - 60 + 2G) aux coins d'un triangle, dans l'écrin d'une roue-180. Le générateur G jouant en effet le rôle de "zéro logique" dans une roue, et la nécessité de différencier les nombres-mondes, conduit à réitérer la roue-60 de base avec un décalage modulo G. Ce qui implique des trous : G=61, 2G=122 et 3G=183 sont absents, et comme au centre de chacune des roues.
En quelque sorte, cet écart entre 360 et 366 ne serait que la sextuple conséquence du "jeu du un" entre 60 et son générateur insécable 61 : le caractère premier de 60+1 est donc une propriété remarquable de plus.Illustration par les cercles colorés + 6 cercles blancs... (pavage de Torres-Heredia Julca).
*
Simple remarque à propos du 1+...
Je lis que la Terre effectue 365 tours 1/4 sur elle-même au cours de sa révolution solaire ; en réalité, 366 tours 1/4 car sa révolution autour du soleil cache un tour sur elle-même : ce qui me semble juste.
Donc, en logique naturelle, pour un mobile en rotation autour d'un foyer et de son axe propre, ce 1+ pourrait correspondre à une rotation propre extrinsèque, liée à cet "engrenage" des deux rotations.*
Au fait, j'avais lu une chose intéressante sur le système sexagésimal : c'est que les diviseurs de 60, qui se groupent évidemment par paires (1-60 / 2-30 / 3-20 / 4-15 / 5-12 / 6-10) ont deux propriétés intéressantes :
- d'abord leur nombre important, qu'on peut également écrire 12 = 10 + 2 (extrémités qui ne sont pas tout à fait des diviseurs, dans l'esprit des nombres premiers par exemple). Ou encore : Poséïdon ("base" 1-60) et ses 5 paires de jumeaux... Quoique ce nombre n'ait rien de hors-norme, voir le graphique (nombre de diviseurs en ordonnées):- ensuite, les diviseurs sont consécutifs : 1-2-3-4-5-6 et situés sous le "breakpoint" qui est
 (dont le sens est bien sûr lié à l'appariement des diviseurs). Il se trouve que 60 est l'unique entier avec un nombre aussi grand de diviseurs consécutifs situés sous le point de rupture. Il est intéressant de remarquer ce "décrochage" au niveau du 7, qui fait écho à l'heptagone régulier non constructible à la règle et au compas.
(dont le sens est bien sûr lié à l'appariement des diviseurs). Il se trouve que 60 est l'unique entier avec un nombre aussi grand de diviseurs consécutifs situés sous le point de rupture. Il est intéressant de remarquer ce "décrochage" au niveau du 7, qui fait écho à l'heptagone régulier non constructible à la règle et au compas.
- enfin, une remarque de Carteret bien utile, liée à la génération du 10 et du 12. Partant des "six directions", on marie les 2 pôles verticaux avec la croix horizontale et son centre, soit 2 x (4+1) = 10 ; réciproquement on marie les 4 directions à l'axe vertical avec son centre, soit 4 x (2+1) = 12. Mariages de 2x5 et 3x4 d'ailleurs illustrés par les couples "canoniques" du tarot (Papesse-Pape, Impératrice-Empereur). De là, comme dans le calendrier chinois, on peut générer le 60 par "engrenage" du 10 et du 12 (= le PPCM).*
Coup de théâtre côté cosmologique. Voilà sa genèse. Je m'intéresse pas mal aux étoiles depuis quelques jours, notamment à la voie lactée et Orion-Sirius. Piobb, un chercheur des plus sérieux eu égard aux mathématiques, écrivait dans sa "Vénus" :
Notre certitude d'hommes terrestres est limitée en quatre plans ou systèmes : le système terrestre ; le système Terre-Lune ; le système solaire ; le système alcyonaire.
Les quatre cercles célestes qui correspondent à ces systèmes (qui en sont les équateurs) s'appellent : l'horizon ; l'équateur céleste ; l'écliptique ou orbite terrestre ; l'orbite du soleil autour de l'astre, centre de toutes les étoiles de première grandeur, que les travaux de M. Charles André ont démontré être Alcyone des Pléiades.Sur la toile, seul le new-age colporte ce genre d'idées exotiques sur Alcyon.
J'ai néanmoins fini par trouver un article en anglais qui commence en disant que les systèmes stellaires multiples sont la règle dans l'univers, et qu'il est pour le moins étonnant que notre Soleil fasse exception. Je te passe les détails mais l'idée est avancée (de manière crédible) que Sirius (en lui-même déjà système double ou triple) puisse être compagnon du Soleil. Avec moins de détails, que Sirius orbite autour d'Alcyon, qui à son tour orbite le centre de la galaxie (situé dans la direction du Sagittaire sur l'écliptique).
Mais le plus étonnant dans cette histoire et auquel je ne m'attendais pas, c'est que le modèle de précession, basé sur la perturbation de l'inclinaison de l'axe terrestre à cause du couple des forces luni-solaires, est remis en cause. En effet, en supposant simplement que le Soleil suive une orbite circulaire, on observera une précession. Nous sommes d'ailleurs forcés à revoir le modèle précédent qui nécessite beaucoup de paramètres ad hoc pour coller aux observations. Ce sont des gens qui me paraissent sérieux qui avancent cela. En particulier, on observe l'invariance des levers et couchers héliaques de Sirius dans le calendrier.
Bref, tout cela me plaît dans la mesure où je ne comprenais pas pourquoi les architectes des anciens monuments cyclopéens notoirement astrosophiques, se seraient donnés tant de peine pour des résultats hautement périssables.*
cerise sur le gâteauIl faut bien reconnaître que l'auteur de l'horloge de Gizeh, même si je m'en méfie un peu, a des intuitions extra. Brindilles synoptiques pour feu-patate :
Il propose une organisation des éléments du tableau périodique avec un octaèdre, qui explique naturellement les lignes un peu bizarres, comme les lanthanides et actinides. Nombre d'éléments max = 120. Cela repose sur un genre de "pavage cellulaire", avec 2 cellules initiales (H et He en l'occurrence), et les enveloppes périphériques auront une taille qui augmente en +4. D'où les nombres 2-6-10-14. Expliquant ainsi que les rangées de Mendeleïev aient 2 éléments, 8 éléments (2+6), 18 éléments (2+6+10) et 32 éléments (2+6+10+14). L'explication complète est un tout petit plus longue mais tu as l'essentiel.
Et il va finalement relier cette structure au carré gnomonique, avec la convention qu'une unité correspond une paire électronique (spins yin-yang).
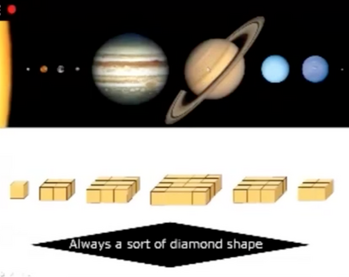
2 = 1 doublet = 1 sphère8 = 2² doublets = sommets de 2 tétraèdres18 = 3² doublets = sommets de 3 octaèdres32 = 4² doublets = sommets de 4 cubes
Il semble en déduire un principe de structuration très général, basé sur l'empilement de ces carrés selon une "forme de diamant" : en commençant par le carré de taille 1 (en général), on augmente puis on redescend dans la taille des carrés ; mais on peut avoir deux carrés consécutifs de même taille (comme dans l'octaèdre des éléments atomiques) et ne pas finir par le carré de taille 1. Sur le plan atomique, cela explique aussi très bien les différents régimes de valence des atomes. Impressionnant.
 *La question est grave : 2 et 3 sont-ils premiers ? Bon, évidemment la définition dit que... Je la fais courte : j'trouve que ça cloche. La seule explication plausible pour le moment, c'est qu'aucun nombre composé n'a encore été généré. Le premier composé est 4. Faut-il qu'on ait goûté à ce "genre" pour apprécier, en fait définir les atomiques? De quoi faire de 5 le prince des nombres premiers. La première tétrade ayant un rôle beaucoup plus "élémental" de structuration du monde, au niveau duquel la notion de primauté ne ferait pas sens ; ce sont des nombres-racines. Enfin, hypothèses...*J'viens de penser à un truc : ces 366 jours annuels, pourquoi ne seraient-ils pas variables (comme le taux de précession), à l'échelle de la Grande Année ? Après tout, si la massive Sirius se rapproche, la vitesse de tous les corps du système solaire devrait augmenter. Envisager que 360 puisse constituer une valeur moyenne ou parfaite, je ne sais pas.Un Âge d'Or pourrait correspondre à une configuration de parfaite consonance (rapports entiers) des divers cycles.*
*La question est grave : 2 et 3 sont-ils premiers ? Bon, évidemment la définition dit que... Je la fais courte : j'trouve que ça cloche. La seule explication plausible pour le moment, c'est qu'aucun nombre composé n'a encore été généré. Le premier composé est 4. Faut-il qu'on ait goûté à ce "genre" pour apprécier, en fait définir les atomiques? De quoi faire de 5 le prince des nombres premiers. La première tétrade ayant un rôle beaucoup plus "élémental" de structuration du monde, au niveau duquel la notion de primauté ne ferait pas sens ; ce sont des nombres-racines. Enfin, hypothèses...*J'viens de penser à un truc : ces 366 jours annuels, pourquoi ne seraient-ils pas variables (comme le taux de précession), à l'échelle de la Grande Année ? Après tout, si la massive Sirius se rapproche, la vitesse de tous les corps du système solaire devrait augmenter. Envisager que 360 puisse constituer une valeur moyenne ou parfaite, je ne sais pas.Un Âge d'Or pourrait correspondre à une configuration de parfaite consonance (rapports entiers) des divers cycles.*Un morceau de choix by Daniélou.
*
Connais-tu cette machine ? Quelques longueurs au début, mais ce documentaire est passionnant !
*
Levers héliaques noté "HR" (heliacal rising)
Un assaut bien mené m'a permis de faire des découvertes intéressantes :
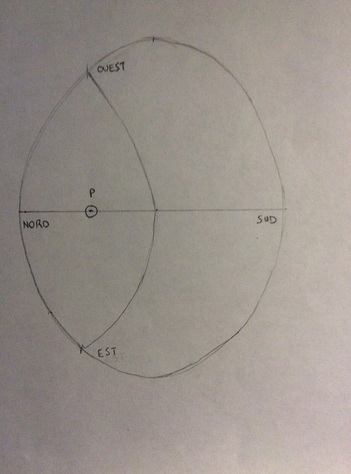
La carte est organisée comme suit :- le centre (EP) correspond au pôle de l'écliptique (cercle rouge)- le premier cercle correspond au trajet des étoiles polaires : j'ai indiqué 3P, 1P et 2P comme étoiles que je prends comme pôles à T = 1, 2 et 3.- le cercle le plus extérieur correspond en quelque sorte à l'horizon maximal visible au cours de la Grande Année, à la latitude choisie ; toutes les étoiles visibles au cours du grand cycle ne le seront pas forcément à n'importe quel moment. Ainsi de Sirius dans ce dessin, qui est trop proche du bord pour être visible pendant toute la Grande Année.- le cercle annoté 1 effleurant le grand cercle, correspond à l'horizon à T=1 ; je n'ai pas dessiné les horizons H2 et H3
Bon maintenant je peux chercher les dates de lever héliaque de Sirius, à l'aide d'une alidade elliptique (inspirée de mon cherche-étoile) : cela correspond à l'intersection de mon ellipse, centrée sur le pôle au temps choisi, avec l'écliptique, lorsque le côté Est de l'ellipse borde Sirius.Pas évident à décrire avec des mots, mais ce qui est intéressant ce sont les résultats :
Entre T = 1, 2 et 3, ce qui balaye le quart du cycle (environ 6000 ans), les levers héliaques sont confinés sur une zone restreinte de l'écliptique, probablement pas plus large qu'un demi-signe. Le mouvement est d'abord prograde puis rétrograde.
Evidemment, les étoiles écliptiques subissent pleinement la précession, comme l'indiquent les points "gamma". L'effet de confinement est lié au fait que Sirius n'est pas très haute dans le ciel à la latitude choisie (je me suis calé sur 45° Nord). Au niveau de l'Egypte, Sirius est néanmoins plus haute, mais on peut s'attendre à un effet qualitativement similaire.
J'espère ne pas t'avoir ennuyée, ni embrouillée.