Dualité mathématique et synthèse a priori

III. DUALITE MATHEMATIQUE ET SYNTHESE A PRIORI

La notion de dualité constitue pour Granger une catégorie philosophique, dont l'acception est dérivée des définitions mathématiques de ce terme, elles-mêmes variées, sans se confondre avec l'une d'entre elles en particulier. Citons l'une des définitions données par Granger de cette notion, - définitions qui, pour être non seulement diverses, mais souvent, comme ici, prudentes et programmatiques, ne doivent pas masquer le caractère urgent et impérieux qu'elles revêtent, sans nul doute, pour leur auteur.

"Au sens où nous l'entendons, la notion de dualité comme catégorie philosophique conduirait à formuler le principe de la nécessité d'une détermination réciproque de tout système d'objets de pensée et d'un système d'opérations intellectuelles associé."

A cette définition liminaire, il faut ajouter cette précision tout aussi essentielle, que, dans le développement de la mathématique, ce qui était objet d'un certain point de vue antérieur, peut, à son tour, devenir opérateur d'un point de vue nouvellement formulé, - la dualité devenant ainsi le vecteur, non seulement de la continuité du raisonnement ou du discours mathématique, mais de la constance d'une certaine forme logique.

La dualité grangérienne a vocation à se substituer à la notion kantienne de "synthétique a priori", dont elle reprend toutefois les réquisitions. Un système opérations-objets dual et consistant peut être considéré comme un "ensemble" synthétique a priori de vérités mathématiques.  Mais la notion  de dualité est aussi intimement liée à celle de nature mathématique, et à la définition de ce que peut être un objet mathématique naturel, dans la mesure où elle tend à associer la définition des objets mathématiques, autant à des lois physico-chimiques de la nature, qu'à des actions concrètes de l'homme, qu'elles soient d'ordre psychique ou physique, - sans exclusion du musculaire, - d'un caractère assez universel, idée qu'avait déjà thématisée, en son temps, la théorie de la forme, ou même la pensée formelle en général. 

Concernant cette catégorie, ce que l'on peut remarquer d'abord est son caractère "moniste", d'une part, parce qu'elle ne s'inscrit pas dans un ensemble de catégories de même niveau, mais se présente comme un véritable "singleton" catégoriel, d'autre part, parce que la dualité elle-même est réellement une, même si elle contient le deux, en ce qu'elle s'exprime, comme on l'a dit, par le maintien ou la constance, d'application en application, d'une certaine forme logique; en quoi elle se veut précisément synthèse; et par où se justifie aussi sa prétention singulière à être apparemment, pour Granger, la catégorie ultime de la science

Dans un cadre différent, qui est celui - métaphysique - de la définition du symbolisme et de la pensée symbolique, René Guénon a, lui aussi, donné de brillantes définitions de la synthèse et du synthétique, qui ont plusieurs traits congruents avec celle esquissée ici. 

Dualité des solides réguliers 

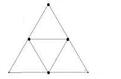
Polyèdres inscrits : tétraèdre                     octaèdre                         icosaèdre 

Polyèdres circonscrits : tétraèdre                  cube                            dodécaèdre

Le tétraèdre, à gauche, est le dual de lui-même. Dans cette relation généralisée, l'ensemble des relations de dualité entre solides réguliers considérés par paires, est déductible, ou dérivable, du développement gnomonique tridimensionnel d'une seule et unique structure géométrique : le triangle équilatéral. En effet, les trois polyèdres primitifs - ici en couleurs et inscrits, dont ceux en arêtes rouges et circonscrits (dans la succession desquels on retrouve les valeurs 3 - 4 - 5 du triangle isiaque) sont les duaux; - ces trois polyèdres inscrits peuvent être construits au moyen de triangles gnomoniques de rang 2 : 1 pour le tétraèdre, 2 pour l'octaèdre, 5 pour l'icosaèdre. Autrement dit : les polyèdres réguliers sont contenus de manière synthétique a priori dans les seules propriétés intrinsèques de développement gnomonique, d'une part, et de clôture géométrique tridimensionnelle, d'autre part, qui sont celles du triangle équilatéral. Ou encore, le triangle gnomonique de rang 2 est la constante logique du système opérations-objets dans lequel consiste et se déploie ici la nature, la définition même des polyèdres réguliers.

tétraèdre + octaèdre + icosaèdre = (1 + 2 + 5) x triangle gnomonique de rang 2

Quant à la série des polyèdres rouges : tétraèdre, cube, dodécaèdre, elle s'obtient par la transformation des premiers polyèdres, d'objets qu'ils étaient, en opérateurs, les sommets de ces polyèdres devenant les centres de référence des faces des polyèdres circonscrits, mathématiquement suffisants à les définir. A leur tour, ces polyèdres rouges peuvent devenir les opérateurs de la construction des trois premiers, par une transformation duale de la précédente.

La synthèse duale revient, comme on le voit, à demander qu'une multitude d'objets et d'opérations mathématiques soient reconduits, ensemble, à l'unité d'un seul principe, d'une seule pensée. En généralisant cet exemple à l'ensemble de la science, on peut le traduire par la réquisition suivante : "S'il y a unité de la science, alors cette unité doit consister en une pensée", - réquisition qui constitue une bonne définition de ce que représente, pour la pensée pythagoricienne, la tétractys.

Dualité et symétrie, deux aspects de la biunité du nombre

Dans sa compréhension profonde, la notion de dualité s'enracine dans la notion pythagoricienne de symétrie, en son sens littéral et originel de commensurabilité, de commune mesure. Une relation de dualité est une relation qui mesure ensemble deux aspects d'une même réalité, qui les tient et les produit ensemble dans un même geste, à partir d'une position "neutre", non polarisée, depuis laquelle ils se transforment l'un en l'autre, - à partir d'un statut originel unique qui n'est, véritablement, ni celui d'opérateur, ni celui d'objet, mais la pure potentialité d'être indifféremment l'un ou l'autre.⁽¹⁾

Une relation de dualité n'est qu'une relation de symétrie forte, développée jusqu'au point où elle est auto-suffisante, (la langue moderne dit avec justesse consistante), c'est à dire productrice, par sa seule potentialité, d'objets et d'opérateurs mathématiques originaux ou "naturels", d'ailleurs indéfinis en quantité.

"Symétrie" et "dualité" ne sont donc que différents noms mathématiques, correspondant à différents degrés de développement, d'une seule et même réalité profonde, qu'on pourrait appeler la biunité du nombre naturel; cet "état" primordial et synthétique du nombre, en lui-même insaisissable, que la logique représente alternativement par les connecteurs "ni... ni...", et "et", dans lequel il n'est, ni objet ni opération, mais l'un et l'autre à la fois, ni cardinal ni ordinal, mais l'un et l'autre à la fois, ni monade ni dyade, mais l'un et l'autre à la fois, voire en pythagorisme conséquent, ni nombre ni figure, mais l'un et l'autre à la fois; biunité dont le principe nous est présenté, par la notion de symétrie, sous son aspect purement arithmétique, et par celle de dualité, sous un aspect géométrique, topologique, et plus généralement structurel, mathématiquement plus développé.

⁽¹⁾ Bien que le sujet ne puisse être abordé ici, on peut remarquer que, du point de vue général de la science, la notion de dualité est presque aussi importante en physique qu'en mathématique; et la description qui en est faite ici pourrait faire penser à l’une des dualités les plus célèbres de la physique, la dualité onde-corpuscule, au fondement de la mécanique quantique, avec d’autant moins de surprise que la théorie ondulatoire est elle-même directement issue de spéculations pythagoriciennes, notamment archytéennes. Dans la recherche plus récente, on peut aussi penser à la théorie des cordes, avec la notion importante de "dualité de cordes".