La construction pythagoricienne de la géométrie

 

    

 

II. LA CONSTRUCTION PYTHAGORICIENNE DE LA GEOMETRIE.

 

 

En dehors de la théorie du gnomon, l'un des aspects les plus importants de la mathématique pythagoricienne réside dans la façon de définir les dimensions et les objets premiers de la géométrie, par une méthode qui est foncièrement différente de celle d'Euclide, en ce qu'elle consiste à associer de façon rigoureuse, à chacune des dimensions ou des objets qu'elle définit, la quantification des opérations de pensée correspondantes à ces objets, comme à ces dimensions. Le référent absolu n'est autre que le temps, mais pas n'importe quel temps, le temps des opérations mathématiques; ici, l'opération : "poser un point dans une nouvelle dimension".

  

1                  2                     3                        4

 

4 objets, 4 dimensions. Le mot "dimension" désignant le fond indéfini des conditions de possibilité propres à chacun de ces objets, il est logiquement impossible, ici, de dénombrer moins de dimensions que d'objets. Objets et dimensions sont déterminés, produits les uns par les autres, dans une relation dont chaque réalité tire sa définition même; sauf à donner de ces réalités une définition ambigüe, mathématiquement non pertinente, comme c'est le cas dans la représentation courante qui ne compte dans l'espace que trois dimensions, où l'on entend par "dimension" une réalité qui peut être parcourue par un quelconque instrument de mesure, alors qu'il n'entre pas dans la nature d'une dimension de pouvoir obligatoirement l'être.

 

*

 

Il est possible de ressaisir le principe de cette méthode dans un cadre épistémologique moderne et rigoureux, qui est la théorie de la forme logique de Granger. Dans le système de Granger, la relation à partir de laquelle est défini tout contenu de science mathématique, est précisément la liaison entre une opération de pensée, (pour nous, un mouvement de la tétractys, une application), et un objet de pensée : l'objet mathématique qui est défini à chaque nouvelle application. C'est exactement le sens qu'il faut attribuer à la sentence pythagoricienne : "Une figure, un pas." A chaque objet défini, correspond une opération de pensée qui est quantifiée et engrammée de façon rigoureuse. Ainsi, dans la construction des objets géométriques, les 4 objets premiers sont d'abord construits synthétiquement, comme dans l'illustration ci-dessus, en utilisant les dix points de la tétractys, puis analytiquement - construction à 24 unités-points -, au moyen cette fois des factorielles des quatre premiers nombres.

  

 

1x1         2x1             3x2x1               4x3x2x1         

 

 

Granger appelle dualité cette corrélation, qui est une relation de cogenèse, de coengendrement, entre une opération mathématique, et un objet mathématique.

Quant à l'archétype de cette relation, sa formulation la plus générale, elle est à rechercher, selon toute apparence, dans la dualité des solides réguliers, qui sera évoquée au chapitre suivant.

 

*

        

A nos yeux, il n'y a que dans la mathématique pythagoricienne que cette méthode de définition conjointe des objets et des opérations mathématiques - méthode dont la réquisition est contenue de façon implicite, pour Granger, dans la notion bien comprise de dualité, - s'avère applicable de façon immédiate, et généralisable à l'ensemble du domaine de la mathématique; sans qu'il soit nécessaire pour cela d'ajouter une abondance de matériel nouveau aux axiomes élémentaires de l'arithmétique et de la géométrie classiques.

Pour le comprendre, il faut, en revanche, se poser la question de ce qu’est l’acte premier, l’acte fondateur de la mathématique.

Et pour éclaircir cette question, dont les racines sont historiques, il n'y a pas d'autre moyen que de revenir aux définitions qui ont été données, dès la plus haute antiquité, de l'objet le plus élémentaire de la géométrie : le point.

Dans cette perspective, comparons le début d’Euclide avec le début de Pythagore.

 

 

Le point euclidien

 

Euclide :

"Le point est ce qui n'a pas de partie".

On veut déjà donner une définition logique. On veut définir l'élément premier à partir d'un lieu de la science qui est ultérieur à lui, puisque c'est lui, le point, qui doit permettre de construire tout le reste. On est déjà dans la conception des modernes, où tout doit être produit à partir de ce qui vient en dernier : la logique.

Or la logique n'est que le vide dont la mathématique est le plein; elle n'est que la forme dont la mathématique est le contenu; elle est incapable de produire un contenu par ses ressources propres.

A l'évidence, la proposition d'Euclide constitue au mieux une définition logique du "zéro" géométrique, ou du bord topologique d'un objet. Ainsi, si l'on considère par exemple un segment, la proposition d'Euclide ne peut, en aucune façon, désigner le premier point de ce segment, mais uniquement le "rien" qui est juste avant et à côté, qui est au contact immédiat de sa "peau" si l'on peut dire; autrement dit la bulle de vide dont ce point s'est précisément soustrait, en tant qu'unité.

Dans la mesure où tout point peut être développé, par projection, dans une indéfinité de directions de l'espace, il paraît hautement risqué de soutenir, comme Euclide, que ces différentes possibilités qui sont toutes constitutives de sa nature, puissent ne pas correspondre à différentes parties de ce point. De fait, la proposition d'Euclide conduit rapidement à des conséquences absurdes.

Si, à partir d'un point, on commence à tracer, dans toutes les directions de l'espace, une série indéfinie de droites émanant de lui, et si en cours de route, on retranche de ce processus ce point lui-même, le "trou" formé au sein du continuum adopte progressivement la structure d'une bulle ou d'un petit sphéroïde; toutefois le contour de ce sphéroïde ne saurait être complètement défini avant que l'ensemble des rayons émanant du point aient été tracés, - ensemble qui se perd bien évidemment dans l'indéfini. D'ici là, la forme du sphéroïde ne sera donc qu'en partie définie. Or, comment une chose qui n'a pas de partie pourrait-elle être en partie définie?

Voilà que nous avons nettement distingué, dans le point, au moins deux parties, une qui est déjà définie, et une qui ne l'est pas encore; mais on comprend que, par induction, ce raisonnement nous contraint à distinguer dans le point une indéfinité de parties, dont chacune est individuellement bien définie par le bord intérieur de chacun des rayons aboutissant à ce point. Le fait que ces différentes parties ne puissent être distinguées au sein du point lui-même par un acte de discrimination spatiale, pour la raison qu'elles s'y trouvent toutes "repliées", confondues et réunies "au même endroit", n'implique en aucune manière qu'elles n'existent pas.

La formule d'Euclide : "ce qui n'a pas de partie" équivaut donc à dire : "ce qui ne peut être développé dans aucune direction"; ce qui est toujours une définition du vide logique ou du zéro géométrique.

Autrement dit, Euclide confond le point avec l'interstice logique purement virtuel, et rigoureusement nul, qui se situe topologiquement entre deux points.

Celui qui énonce : "Il existe un ensemble, appelé zéro, qui ne contient pas d'ensemble", ne fait à l'évidence que répéter la proposition : "Le point est ce qui n'a pas de partie." Comme la proposition d'Euclide, la définition du zéro qui, dans certaines versions de la théorie des ensembles, présente cet "ensemble vide" comme l'ultime contenu de la mathématique, sur lequel s'appuie la définition, ontologiquement ultérieure, de l'unité, (elle même définie comme le premier ensemble qui contient zéro), est sans consistance mathématique. Sans même être fausse, elle ne peut, par sa nature, donner matière à aucune mathématique digne de ce nom.

Ces deux propositions qui, dans leur compréhension juste, désignent respectivement le "zéro" géométrique et le "rien" arithmétique, (deux notions qui, en mathématique pythagoricienne, coïncident elles-mêmes dans celle du vide logique, qui en est la réunion synthétique), ne sont pas consistantes mathématiquement; parce que l'on n'a en rien réussi à produire l'élément premier de la mathématique, lorsqu'on s'est contenté de définir l'une de ses conditions de possibilité, d'ailleurs particulière, en ce qu'elle ne concerne, dans chaque cas, que l'un de ses aspects.

D'une façon plus générale, le point commun à de nombreuses approches modernes de la mathématique, qu'elles soient logicistes, ensemblistes ou axiomatisantes, aura été d'admettre comme "pari" ou comme "foi" scientifique originelle, le postulat que la mathématique est une phrase, que son être consiste dans une phrase, et que donc on peut le présenter dans une phrase, une proposition logique; présupposé qui était déjà manifestement celui d'Euclide. Or l'être de la mathématique ne peut pas consister dans une proposition logique, (comme il sera montré plus loin de façon évidente), parce que la mathématique ne devient une proposition logique qu'à partir d'un certain moment, qu’on qualifiera volontiers de moment opportun. Et il est impossible de dégager, de définir correctement ce moment opportun, si l'on n’a pas compté les différents mouvements qui ont dû être accomplis auparavant.

Si l’on compte à l’envers, - la manie des modernes, - ou si l'on essaie d'engendrer les premières opérations à partir des dernières, on échouera à chaque fois; et l’on parviendra toujours à des conclusions du genre : "Ce sont les irrationnels qui engendrent les rationnels".

Voilà quelques unes des raisons qui peuvent expliquer que le moment logique, - le gnomon - soit resté jusqu’ici inaccessible à l’intelligence des modernes.

 

 

Le point monadologique ou "arithmo-géométrique" pythagoricien

 

Début de Pythagore :

Dix points sont présentés dans la pensée :

 

 

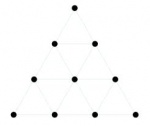
Pythagore est conscient que l'atome, l'élément premier de la géométrie, ne peut être défini par rien de plus originaire que lui-même, sans tomber dans d'insolubles paradoxes,  mais qu’il peut seulement être produit, montré, présenté dans la pensée. Encore n'est-ce possible qu'en l'articulant sous la forme d’une structure, d’un champ. Ce n'est que de la considération  des relations existant entre ces points, telles que symétries ou homothéties, qu'une définition plus précise de l'élément, ou de l'objet premier pourra se dégager; et celui-ci reçoit alors un statut bivalent, à la fois arithmétique et géométrique, qui est celui d'"unité-position", ou "unité ayant position".

De cette manière, on évite de construire la mathématique, comme Euclide, à partir d'une définition qui n'a pas de sens mathématique. La force de la mathématique pythagoricienne consiste toute entière dans cette sagesse, dans cette « prudence » du commencement. Mais aussi dans l'application rigoureuse, jusqu'à l'échelle la plus élémentaire, de la règle qui consiste à définir les objets mathématiques, à partir des seules opérations de pensée qui les engendrent. Une figure (un objet), un pas (une opération) : et l’on quantifie. 

Un point de l'espace, un coup de temps.

Une position du continuum, une unité arithmétique.

Une monade.

 

 *

 

Au fondement de la pensée pythagoricienne, il y a cette conviction que l'essentiel, en mathématique, ne peut être évoqué que de manière allusive et métaphorique, - que ce puisse être en image ou en mots ne changeant, fondamentalement, pas grand chose au problème; - et cela, au moyen d'une balance très prudente entre "ce qu'il nous importe profondément de montrer" et "ce qu'il est réellement possible de faire".

La science, pour Pythagore, consiste dans un rapport réfléchi entre le visible et l'invisible, entre le dicible et l'indicible, qui d'une part, lui impose d'intégrer dans ses méthodes, dans sa façon de faire, le problème des limites concrètes de la représentation, qu'elle puisse être figurale, symbolique, ou langagière, et d'autre part,  lui impose d'installer ou d'instituer, dans ses axiomes, à côté de la dimension du défini, (qui est la dimension de ce qui importe mathématiquement, de ce qui est déjà réuni, recueilli et connu dans le "secret", la certitude ou la foi de l'intelligence, et sur lequel va s'appuyer avec une confiance aveugle tout le reste : "les points sont équidistants", "au nombre de dix", "distribués en symétrie hexagonale", "forment un triangle équilatéral", etc.), la dimension de l'indéfini, de l'à peu près et du vague; dimension que la mathématique ne refuse ni ne refoule aucunement par principe, mais qu'elle assume au contraire régulièrement dans sa pratique quotidienne, et que la mathématique pythagoricienne se contente de revendiquer de façon plus affirmative, sur un plan plus radical, qui est celui des principes fondamentaux.

C'est dans l'assomption de cette limite absolue de la représentation que réside l'originalité de la tétractys. Sur le plan du langage logique, l'équivalent du point monadologique ou "arithmo-géométrique" pythagoricien, ce point qui a comme propriétés apparentes d'être plat et assez gros, et comme propriété essentielle d'être de dimension indéfinie, n'est donc pas l'identité, - identité qui, en elle-même, n'est susceptible d'aucune représentation, puisque toute représentation, toute forme, suppose un processus de différenciation matérielle, qui est contradictoire avec l'identité, - mais plutôt une sorte de reflet de l'identité, déjà forcément diffracté. 

Car le langage logique ne contient pas, lui non plus, la possibilité d'une définition de l'identité sur laquelle s'appuie sa propre consistance, et dont il ne peut faire mieux que de produire, au commencement des choses, des exemples élémentaires différenciés tels que "p", "q", qui par la suite serviront de référence. Toute proposition logique qui tenterait de définir l'identité ne peut, par nature, qu'être contradictoire ou inconsistante; et donc, ne peut pas être au sens propre une proposition logique, mais, au mieux, une image ou une métaphore.

Ainsi, la logique prédicative connaît deux images, - forcément paradoxales, puisque l'identité véritable est ce qui ne tolère, quant à soi, aucune forme d'"altérité", - non pas précisément de l'identité, mais de deux différents mouvements vers l'identité, mouvements dont l'un est ouvrant ou centrifuge, le connecteur "ni..., ni..." ("une tache ni bleue ni triangulaire") et dont l'autre est fermant ou centripète, le connecteur "et", qui attribue deux propriétés (et pas davantage, sauf à renouveler l'opération) à un être ou objet unique, ("une tache rouge et rectangulaire"). ⁽¹⁾

 

NI......................ET.....................NI

 

De la même manière exactement, le point monadologique pythagoricien pourra, très avantageusement, être considéré comme un processus "fermant-ouvrant", ou "inhibiteur-activateur", comparable au mécanisme d'un parapluie, (en langue mathématique, un tenseur binaire, quantitativement indéfini), dont l'axe "ni..., ni..." ci-dessus représenterait le diamètre apparent, et la position "et" la coordonnée mathématique, définie par la relation que ce point entretient avec les autres membres de la constellation, quelque soit la méthode choisie pour paramétrer cette dernière.

Là réside, peut-être bien, le fond de la foi mathématique, dans la confiance que l'identité "insaisissable" se repose, très paisiblement, dans la réunion synthétique des connecteurs "ni..., ni..." et "et".

L'essentiel n'est ni la propriété "a", ni la propriété "b", (propriétés qui sont néanmoins, par hypothèse, les seules que l'on sache ou puisse concrètement montrer, et qui sont précisément toujours des propriétés telles que "plat", "noir", "rond", "assez gros" ou "à gauche"), mais l'être qui, sans être deux, les contient l'une et l'autre "en même temps", ("à la fois" ou "ensemble"), et n'est rien d'autre que leur compossibilité même.

Formule qui n'est toujours pas une définition de l'identité, mais qui est en revanche une définition en mode logique de la synthèse, en tant que méthode de régression intellectuelle progressive, prudente et patiente, du visible indéfini à l'invisible défini, d'abord, puis, de ce connu, de ce défini, à l'ensemble des possibilités mathématiques qui sont nées avec lui, parce qu'elles sont contenues dans sa définition ou dans son être même; - méthode que l'on peut caractériser par des expressions telles que "retroussement", ou "développement  continu", dans laquelle, à aucun moment, ne peut être perdu le contact avec l'image installée au début dans la pensée, et restée depuis présente au fond de celle-ci, comme une pierre de témoignage. ⁽²⁾

 

 

*

 

Ce sont d'autres définitions de la synthèse, plus mathématiques celles-là, qui seront évoquées au chapitre suivant.

 

 

 

 

⁽¹⁾ L'apparence paradoxale de ces formulations, en tant qu'elles se rapportent à l'identité, à l'unité, et finalement à l'être, provient de ce que, dans un cas,  l'identité, ou l'unité, est représentée comme "ce dans quoi peuvent rentrer, ou se réunir deux ("autres") choses"; tandis que, dans l'autre cas, cette même identité, cette même unité est représentée négativement comme "ce qui peut être séparé, distingué radicalement de deux ("autres") choses". La nature même du langage fait qu'il est impossible de s'approcher davantage d'une définition correcte de ce dont il s'agit; alors que ce dont on voudrait parler, et qui peut seulement être objet de foi ou d'intuition, consiste précisément dans la réunion synthétique et non contradictoire des idées contenues dans ces deux représentations.

L'identité est comparable à l'enfant de deux parents, mais un enfant qui, après s'être différencié de leurs deux corps, continuerait d'être une partie intégrante de chacun d'eux, un élément ou un membre à part entière de leurs personnes. Un enfant de cette sorte n'est ni son père, ni sa mère; mais à la fois son père et sa mère.

L'enfant est l'unité et l'identité. L'enfant est la monade qui, selon la tradition, "contient la dyade".

 

⁽²⁾ Le point pythagoricien est suffisamment défini, mais pas trop; et c'est en cela qu'il représente essentiellement du devenir et du "travail".