La divine distance

 

 

LA DIVINE DISTANCE

 

 

par Axel SCHNEIDER

 

  

Pour la commodité du lecteur, on a regroupé sous ce titre les six commentaires postés en septembre 2012 par Axel Schneider, à la suite de l’article : Spirale de Théodore et polygone gnomonique de rang 4. Ceux qui voudraient en savoir plus sur les idées de M. Schneider, et notamment sur la nature de ce fameux ratio mesurant, selon lui, une limite indépassable de la connaissance humaine, pourront se rendre avec profit sur le site personnel de l’auteur :

www.maformulederamanujan.org

 D'autres précisions sur le site de "l'homme de Vitruve" :     

http://screencircles.wordpress.com/2008/01/03/lhomme-de-vitruve/

 

 

 

1.

 

Mardi 4 Septembre 2012

 

En fait, je suis d'accord avec toi pour dire que tous les gnomons sont équivalents quand on considère les polygones réguliers. Le problème vient du cercle (ou plus exactement du disque) : ce n'est pas un polygone avec une infinité de cotés ou en tous cas pas plus qu'un polygone avec un seul côté. 

Dès lors, oui, le gnomon est bien la notion archaïque, sauf qu'elle nous conduit à affirmer avec Gödel que épistémologie/ontologie est inférieur strictement à 1. La question est de savoir quel est ce ratio… Cela ne concerne pas seulement les mathématiques, mais toute connaissance humaine ou surhumaine. Ce ratio ne peut être dépassé que par un concept que l'on peut appeler Dieu ou Oracle (comme Turing) mais qui pour moi n'a aucune vérité en soi, à moins de considérer que la connaissance de ce ratio confère a celui qui la détient cette vérité complète.

Nicolas de Cues était le précurseur de Gödel quant à propos de la question de la transcendance de pi (la quadrature du Cercle), il affirmait :

"(ceux) qui ont cherché la quadrature du cercle ont présupposé la coïncidence du cercle et du carré dans l’égalité, laquelle n’est assurément pas possible au niveau sensible. Car il n’existe pas de carré qui ne soit inégal à n’importe quel cercle engagé dans la matière. Cette égalité, qu’ils ont présupposée, ils ne l’ont donc pas vue avec leurs yeux physiques, mais avec leurs yeux mentaux, et s’ils ont essayé de la démontrer par le raisonnement, ils ont cependant échoué, puisque la raison n’admet pas la coïncidence des opposés. C’est intellectuellement qu’ils auraient dû chercher la coïncidence dans ce cercle qui est égal dans chaque polygone "

C'est la même chose que de dire que tous les gnomons sont identiques. Sauf que dès lors il faut admettre une incomplétude, une dualité du gnomon dans la mesure où le choix canonique entre la factorielle de 0,  0!=1 et 0!=-1 n'est pas symétrique au choix canonique entre i^2=-1 et i^1/2=-1. Il existe un isomorphisme entre le gnomon des réels et le gnomon des imaginaires, mais le gnomon complexe n'est pas atteignable sans une "approximation"  (le foncteur d'oubli du plan complexe considéré comme une surface de Riemann universelle).

 

 

2.

 

Mardi 4 Septembre

 

Seul compte le corps des complexes, la clôture algébrique du corps des réels sur le corps des nombres imaginaires : c'est l'unique représentation possible de l'espace sensible et, comme je l'ai dit, sur cet espace sensible, le gnomon "complexe" est obligatoirement dual, c'est à dire que le gnomon "véritable" n'est pas accessible au sensible. 

Cela se décline selon moi : avec l'inégalité isopérimétrique (rappelez vous de la création de Carthage par Didon...). Dans ce cadre, le cercle et le triangle équilatéral sont des extremums : le cercle est le "polygone" qui par rapport au "périmètre" (circonférence) a la surface la plus importante et le triangle équilatéral celui qui pour le même périmètre a la plus petite surface. Le carré est donc le premier polygone et permet de calculer le cycle d'obstruction... C'est ainsi que l'on trouve la construction de Vitruve.

On a alors en reprenant votre logique 2 carrés gnomiques et non un seul (car alors le centre du cercle et le centre du grand carré vitruvien sont distants d'une unité). Le carré gnomon de rang 5 qui se décompose en 2 rectangles : l'un de 4 sur 1 et de diagonale racine 17 et l'autre de 4 sur 5 et de diagonale racine de 41, et le carré gnomon de rang 4 qui se décompose alors en 2 rectangles, le rectangle de 4 sur 1 (le même que précédemment) de diagonale racine de 17 et le rectangle pythagoricien (triangle isiaque) de 3 sur 4 et diagonale 5.

 

 

La tradition compagnonique reprise par les traditions maçonniques, considère le problème ainsi : on ne peut pas mieux faire comme polygone gnomique complexe que le carré long de 3 sur 4. Donc, dans ces traditions le fameux ratio correspond à la surface du carré long divisée par la surface du carré possédant le même périmètre de 14. On trouve ainsi un ratio de 12/12,25 soit un peu plus de 97 %. L'incomplétude dans cette logique serait donc d'un peu plus de 2 % seulement... C'est très faible (et donc forcément très subversif pour les Eglises) et en même temps très important pour les positivistes car, cet univers platonicien nous est bien inaccessible (mais l'on saurait si cela est exact à quelle divine distance de nous il se trouve).

Je ne serai pas plus long pour le moment, mais il faut bien comprendre le phénomène d'obstruction : c'est la parabole de la pêche miraculeuse partagée par Pythagore selon Jamblique et par le Christ selon Saint Jean (tiens le Christ aurait reçu un enseignement pythagoricien? Peut-être est-ce le fils d'Isis et d'Amon-Osiris comme pouvait l'être, par exemple, Césarion-Horus...) Les poissons ce sont les vesica piscis, 1/2 de la racine de 3, les mailles du filet, le polygone gnomique de rang 4 : reste toujours 153 = 1!+...+5! = 1+...+17...

 

 

3.

 

Mardi 4 Septembre

 

Tout d'abord, diverses représentations du carré long de 3 sur 4 dans les traditions maçonnique et chrétienne : 

 

               

                    

  

Et le double centre de la construction de Vitruve chez les Templiers :

  

 

  

4.

 

Mercredi 5 Septembre

 

Votre remarque sur la conception Euclidienne, "le point est ce qui n'a pas de parties" et celle plus monadique (dans le sens de Leibniz) de Pythagore "10 points sont montrés ou présentés dans la pensée" (le Tetracktys) est particulièrement bien venue. 

Etienne Klein, physicien spécialiste de la question du temps, a bien fixé le cadre qui a animé de vives discussions entre Stephen Hawking et Roger Penrose en 1997 sur la Relativité générale. En effet, le cadre théorique relationnel de la RG (continuum espace-temps), puisqu'il ne peut jamais être "vide" absolument : il existe toujours un tenseur métrique, un champ qui ne s'annule jamais "en tout point" du continuum. Comme les équations de Maxwell traitent du champ électromagnétique, les équations d'Einstein traitent de ce champ. Ainsi la RG, qui se veut une vraie théorie par rapport à l'approche de Newton qui retient l'espace et le temps comme des absolus (je dirais même la matière et donc la gravité), n'existe pas sans sa métrique. Or pour définir un champ, il faut définir ce champ : l'approche pythagoricienne du Tetracktys me semble tout a fait adaptée puisqu'il s’agit comme vous le dites d'un ensemble de 10 points, un champ logique. Le tenseur métrique ne s'annule en aucun point "euclidien" : en clair, pas d'annulation, pas de singularités (style trou noir) dans la RG car sinon il faut considérer la disparition de la métrique. Sauf à considérer, comme le très pythagoricien (selon moi) Aristote, que le 1 n'est pas un nombre mais une idéalité platonicienne inatteignable...

 

 

5.

 

Mercredi 5 Septembre

 

Je trouve très intéressante l'idée de dire que quel que soit le polygone régulier envisagé, eh bien le gnomon est "équivalent" (à n-près) et de parler de polygone gnomique plutôt que de gnomon.

C'est comme l'approche pythagoricienne de N. de Cues qui affirme qu'il n'existe "pas de carré qui ne soit inégal à n'importe quel cercle". Il ne dit pas que la quadrature du cercle est possible, il dit juste que comme le cercle (disque) partage avec le carré (et donc tout autre polygone régulier) les concepts de longueur (D1) (circonférence) et de surface (D2) (aire), eh bien intellectuellement ils sont "égaux" mais que cette similitude n'est pas perceptible au niveau "sensible". Je pense que dans l'esprit de N. de Cues, en tous cas dans celui de L. de Vinci et de la "petite école cusienne d'Italie" eh bien la cause de l'impossibilité d'une quadrature était acquise, bien que la démonstration ne viendra qu'au 19ème siècle. Dans l'esprit "cusien", la transcendance (le mot est anachronique) de pi n'est donc pas le signe d'une "inégalité" mais d'une obstruction, une homologie ou plus exactement une cohomologie (là encore ce sont des anachronismes), c'est à dire l'obstruction qu'ont certaines suites de morphismes (deux ensembles avec une même structure comme par exemple dans le cas d'espèce les polygones et les cercles) à être exactes.

Ainsi le raisonnement que l'on fait sur le carré est valable à n-près pour n'importe quel polygone régulier (du triangle équilatéral au polygone avec une infinité dénombrable de cotés). 

Attention ! Je dis bien un polygone avec une infinité dénombrable (au sens de Cantor donc avant diagonalisation vers l'infini indénombrable des Réels) de côtés. Dans mon idée, un polygone avec une infinité indénombrable de côtés, c'est un cercle.

L'idée de rajouter l'hypothèse du continu (ou du discret) à l'ensemble des axiomes d'une théorie formelle capable de formaliser l'arithmétique et récursivement axiomatisable (logique du 2nd ordre) ne change rien au fait qu'elle contient des propositions contradictoires (consistance) ou indécidables (complétude). Il résulte en fait des travaux de Gödel de 1938 et de Paul Cohen de 1963 (avec sa célèbre méthode de Forcing) que l'hypothèse du continu est indécidable. Donc, pas plus de complémentation avec l'axiome du continu qu'avec n'importe quel axiome (comme l'axiome de protection de la chronologie de Stephen Hawking pour la relativité générale...). Ainsi, on ne sait pas si il y a des trous ou non dans la droite réelle, c'est à dire si le cardinal transfini de l'infini indénombrable des réels (aleph 1) est le successeur immédiat du cardinal transfini de l'infini dénombrable (aleph 0).

L'idée de l'angle d'attaque est donc de dire (un peu comme l'intrication quantique) qu'au niveau "sensible" (au sens de N. de Cues), eh bien il faut considérer que les 2 sont vrais et que l'on ne peut pas calculer le cardinal aleph 1/2 soit parce qu'il n'existe pas et que la relation d'ordre entre aleph 0 et aleph 1 est "séparée" par rien ou plus exactement un objet qui n'est pas défini dans les mathématiques, soit parce que l'on ne peut connaître la position absolu de aleph 1/2, les trous dans la droite réelle n'étant alors pas calculables exactement.

Ces deux hypothèses au niveau "sensible" sont donc identiques en dernière analyse... Mais, il y a selon moi un mais, puisqu'au niveau "sensible", on démontre en tous cas des "trous" logiques (qu'ils soient virtuels ou réels) et peut-être que l'on peut calculer l'importance de ces trous à défaut de les situer.  

J'ai déjà montré comment Léonard de Vinci (et bien entendu Vitruve) envisageait la question : c'est l'unité isopérimétrique. On a beaucoup dit que l'homme vitruvien était la représentation des mensurations de l'homme idéal... Oui et non : la perspective de Vitruve c'est de mesurer la "divine distance", c'est à dire "si" "Dieu" a fait l'homme à son image (parfaite), dans quelle mesure l'homme (ou Dieu par récursivité...) peut-il appréhender la "pensée divine" (la vérité). Vitruve parle de cela d'ailleurs dans la partie de son "de Architectura" consacrée à la construction des temples (comme le mythe compagnonique et franc-maçon de la construction du temple de Salomon : l'équerre et le compas avec la question du centre de gravité G). Vitruve (et le Vinci) veulent mesurer ainsi le rapport entre l'ontologie (la sémantique) et l'épistémologie (la syntaxe), la "divine distance".

Voilà l'idée de Vitruve... et celle d'Emil Post : mesurer le RE Turing degree universel, que l'on peut formuler selon moi ainsi : "Quel est le plus petit x qui permet d'avoir une théorie capable de formaliser l'arithmétique (structure algébrique ternaire), récursivement axiomatisable à 100 %, consistante et complète au sens de Gödel?"

 

 

  

Le centre du cercle, et celui du carré : dans la construction de Vitruve on retrouve l'"égalité" de N. de Cues c'est à dire que le rapport entre le côté du carré et le rayon du cercle quand on les met dans une relation triangulaire (puisqu’on ne peut distinguer entre les 2 extremums du triangle équilatéral - minimun isopérimétrique dénombrable - et le cercle maximum isopérimétrique indénombrable) est de 8/5 unités, l'unité étant la "distance" entre le centre du cercle et celui du carré (la métrique qui ne s'annule en aucun point de l'espace-temps relativiste...)

Bon et quid du Gnomon ?

Le Gnomon c'est 2n+1. Mais, pour les nombres imaginaires ? 2n-1.

Maintenant, sur le plan complexe ? Et bien, c'est là où l'unité du Tretracktys : le Tretracktys en tant que théorie formelle ne peut servir à axiomatiser complètement la "théorie formelle" (méta-modèle) et donc conceptualiser complètement le gnomon complexe.

L'unité gnomique de référence est donc le gnomon de rang 4, le gnomon quadratique. On ne peut aller en dessous. Ainsi on a une rupture de symétrie entre la plus petite chaine de Cunningham (chaîne de nombres premiers) de type 1 (2n+1) et de poids 5 (4 itérations) : 2, 5, 11, 23, 47 et  la plus petite du type 2 (2n-1) et de même poids qui commence par 1531 :

1531 3061 6121 12241 24481

Pourquoi ce 1531 : car 1!+...+5! = 1+...+17 = 153

Rappelons que la somme infinie de l'inverse des factorielles nous donne le nombre e, base des logarithmes népériens. Mais contrairement à ce que pourrait laisser penser l'identité d'Euler eî.pi = -1 (donc Dieu existe disait Euler à Diderot à la Cour de la Grande Catherine...) : la transcendance de e et de pi ne sont pas forcément équivalentes dans le sens où l'on peut avoir des nombres transcendants comme e avec une mesure d'irrationalité  égale à 2 comme pour les irrationnels algébriques (par exemple les racines des nombres premiers). On ne connait pas la mesure d'irrationalité de pi (enfin moi je crois que si : on prend juste mon ratio et 2+2*2,08 %).

Ainsi, si effectivement les log naturels permettent de faire d'une multiplication une addition, on peut montrer la convergence vers pi de la moyenne arithmético-géométrique (AGM) de 1 et 1/racine de 2 (cf. la formule de Brent-Salmin).

 

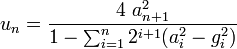
Sauf que la vitesse de convergence de la somme des inverses des factorielles vers e est peut-être plus rapide que la convergence de la moyenne AGM de 1 et de 1/racine de 2 vers pi.

(la suite prochainement)

 

 

6.

 

Vendredi 14 Septembre

 

La recherche des bonnes proportions entre le diamètre des colonnes des temples et leur hauteur a conduit dans la Grèce antique aux différents ordres architecturaux (on en recense 5 traditionnellement mais les plus importants sont les ordres dorique, ionique et composites). La question qui se posait était bien évidemment la quadrature du cercle.

 L'ordre Dorique semble privilégier le carré "vitruvien" plutôt que le cercle "vitruvien" : 8 plutôt que 10. A l'inverse, l’ionique privilégie plutôt le 10 par rapport au 8. Les ordres composites "tâtonnent" entre ces 2 extrêmes. Vitruve nous montre que la divine proportion n'est atteignable que de façon approximative (le carré long).