-
Pavages cellulaires
PAVAGES CELLULAIRES
par Guillaume DENOM
"On remarque que la série des hexagones cellulaires est identique à celle des gnomons du cube."
ARGUMENT : Le nombre figuré et le nombre polygonal sont deux procédés traditionnels visant à représenter des nombres par des figures. S'ils bénéficient d'une certaine popularité dans le grand public, ils sont peu considérés des mathématiciens, en raison d'un préjugé - justifié - d'inintérêt, ou d'inintelligence mathématique.
Les défauts de ces théories peuvent se résumer en deux points :
1. Le déploiement de la série des polygones dans un même plan est impuissant à rendre compte des problèmes de symétrie très singuliers auxquels renvoie individuellement chacune de ces figures. Ainsi le carré, le pentagone et l'hexagone, renvoient à trois problèmes de symétrie très différents, et non homologues, et qui nécessiteraient, pour être exprimés de façon pertinente par des nombres, de déployer d'autres dimensions que celle du plan.
2. Les deux théories souffrent d'un défaut rédhibitoire, qui est le statut paradoxal du point, lequel devrait, selon leurs attendus, être à la fois un triangle, un carré, un hexagone, et bien d'autres choses encore.
Ce raccourci non exhaustif (bien que logiquement suffisant) du problème, nous est imposé par le fait qu'il existe, en réalité, plusieurs théories du nombre figuré, comme du nombre polygonal, cette dispersion même étant l'indice du fait qu'il n'existe, en vérité, aucune théorie mathématique digne de ce nom, derrière ces représentations diverses.
Malgré ces défauts, le succès de ces représentations semble traduire un sentiment latent, qu'il y a, peut-être, quelque chose d'intelligent à vouloir associer nombres et figures. La théorie des pavages cellulaires permet de rouvrir ce débat d'un point de vue a priori modeste et convivial, qui est celui de la logique élémentaire, et de lui apporter une réponse positive.
La théorie des pavages cellulaires constitue un ensemble de lois mathématiques qui, habituellement, sont abordées par deux approches mathématiques différentes : les problèmes d'empilement compact de cellules discoïdales ou sphériques, d'une part, et les problèmes de tessellation - ou de pavage - du plan ou de l'espace, par des polygones ou des polyèdres, d'autre part.
Nous allons voir que cette séparation des approches n'est pas nécessairement justifiée, dans la mesure où la théorie des pavages cellulaires se situe précisément à l'interface entre ces deux domaines.
Pour commencer, les idées physiques associées à la notion d'empilement compact pourraient même, ici, susciter une certaine confusion. En effet, au sens physique, les carrés et les cubes cellulaires sont considérés comme des structures « non compactes ». On veut dire par là qu'on ne peut les engendrer en laissant agir une force telle que la pesanteur. Les cellules ne se rangent pas « toutes seules ». Mais un peu de réflexion nous convainc que les pavages qualifiés de compacts, tels que les pavages hexagonaux, ne le sont, dans l'absolu, qu'en raison des forces physiques qui s'exercent sur eux de l'extérieur, dans l'environnement qui est le nôtre. A l'échelle microscopique, où l'action de la pesanteur devient négligeable, la nature ne montre aucune répugnance pour les arrangements cubiques, puisque ceux-ci abondent dans les systèmes cristallins ; et il est assez simple de créer un système de forces où, même à l'échelle macroscopique, les empilements cubiques s'avèrent aussi « stables » ou « compacts » qu'on peut le souhaiter, au moyen de billes magnétisées par exemple. Dans notre approche, qui est avant tout topologique, tous les systèmes doivent donc être envisagés comme virtuellement « compacts », au sens de « solidaires ».
Quoiqu'il en soit de ces questions, nous allons voir qu'en mathématique pythagoricienne, le traitement des pavages cellulaires dans une théorie unitaire et indépendante est justifié par deux raisons suffisantes.
- Ils se prêtent à une classification quadridimensionnelle analogue à celle des objets gnomoniques, comme à celle des objets fondamentaux de la géométrie pythagoricienne.
- Comme la théorie du gnomon, ils se rapportent au problème logique de la reconstitution d'objets, (fondamental en mathématique pythagoricienne, et qui relève, en soi et pour soi, de contraintes logiques plus sévères qu'on ne le suppose habituellement), dont ils prolongent et complètent la théorie.
Dans le tableau ci-dessous, les cellules 2D (cercles ou disques) sont représentées en noir, et les cellules 3D (sphères ou boules), en d'autres couleurs.
CLASSIFICATION QUADRIDIMENSIONNELLE DES ELEMENTS
Dimensions
euclidiennes D2
D3 Dimensions
pythagoriciennes
P1. POINTS
(1, 1, 1, 1, ...)

P2. SEGMENTS
(2, 3, 4, 5, …)


P3. PLANS
(Polygones cellulaires)
Triangles
(3, 6, 10, 15, ...)
Carrés
(4, 9, 16, 25, ...)
Hexagones
(7, 19, 37, 61, ...)






P4. SOLIDES
(Polyèdres cellulaires)
X Tétraèdres Cubes
(4, 10, 20, 35, ...) (8, 27, 64, 125, ...)
tétraèdre de rang 6 cube de rang 5
83 cellules 216 cellules
Octaèdres Cuboctaèdres
(6, 19, 44, 85, …) (13, 55, 147, 309, ...)
octaèdre de rang 6 cuboctaèdre de rang 10
231 cellules 3871 cellules
Pour chaque catégorie d'objets, la formule entre parenthèses donne en gras la valeur du plus petit élément insécable de sa classe, et à sa suite la série des valeurs pour lesquelles l'objet est reconstitué, par l'adjonction de cellules à cette structure de base. On remarque que l'objet « Point » ne peut, par nature, être « reconstitué » que par l'ajout répété de « zéro cellule », qui le laisse inchangé ; tandis qu'à l'opposé, l'objet « Segment » est reconstitué pour toute valeur entière supérieure à 2.
Dans l'absolu, il n'y a pas de nécessité à ce que les cellules soient jointives, la contrainte de « compacité » pouvant, à loisir, être remplacée par toute autre contrainte de répartition qui conserve les propriétés des structures. Mais pour cette étude introductive il a paru avantageux de considérer le cas le plus simple : celui de cellules de même dimension, empilées de façon compacte, sans discontinuité.
De la même manière, pour la classe des polygones, il a paru pertinent de se limiter dans un premier temps aux trois polygones qui, en version « classique » (non cellulaire) pavent le plan, savoir : le triangle équilatéral, le carré et l'hexagone.
Ces deux restrictions conduisent à exclure de la présente nomenclature des polyèdres tels que l'icosaèdre cellulaire qui, en raison de sa structure pentagonale, n'est constructible qu'en tant que surface, mais nécessite de ménager, à l'intérieur de l'objet, une région vide, où la périodicité des empilements est interrompue, - le pentagone n'étant pas une solution de pavage continu du plan.
icosaèdre cellulaire
La famille des polyèdres pourrait néanmoins, sans déroger aux règles définies ici, s'enrichir de diverses de curiosités géométriques résultant, comme les structures ci-dessous, de la troncature de solides pythagoriciens classiques ; mais là encore on a jugé bon, dans un tableau élémentaire, de s'en tenir à l'appareil le plus réduit possible.

exemples de polyèdres compacts engendrés par divers automates cellulaires, construits sur un réseau dodécaédrique rhombique
Quant aux structures non continuellement périodiques, comme celle de l'icosaèdre cellulaire, elles pourraient, elles aussi, être intégrées dans une classification plus large, définie dans le prolongement de celle-ci ; en tenant compte du fait que, du point de vue essentiellement génétique, ou généalogique, qui est celui de la logique pythagoricienne, elles relèvent d'un type moins simple, ou moins primitif, que celles du tableau ci-dessus. La remarque valant, également, pour les structures construites avec des sphères de dimensions différentes... - ou en modifiant encore d'autres paramètres.
On remarque que, dans cette logique, les dimensions « euclidiennes » D2 et D3 se présentent comme des « cas particuliers » des dimensions pythagoriciennes P1 à P4, qui relèvent d'un statut logique « plus général ».
Cette analyse quadridimensionnelle n'aura rien de déroutant pour les familiers de la mathématique pythagoricienne. On a vu dans une précédente étude que le Lambda de Platon était associé à une analyse quadridimensionnelle des propriétés du cube, dans laquelle les jambes gauche et droite du Lambda correspondent, respectivement, à la composition des cubes gnomoniques de rangs 2 et 3. Dans le cube gnomonique, c'est le petit cube atomique de valeur 1 qui joue le rôle de point.
Enfin, la même analyse quadrimensionnelle est associée, dans la tradition pythagoricienne, à la classification des objets fondamentaux de la géométrie en deux séries quaternaires : les objets premiers d'une part, les objets monadiques d'autre part.
LE PROBLEME LOGIQUE DE LA RECONSTITUTION D'OBJET
Il importe de bien distinguer la présente approche d'autres nomenclatures bien connues, auxquelles le lecteur a pu être confronté, comme celle des nombres polygonaux, ou celle des nombres figurés.
Ainsi, en apparence, la série des « triangles cellulaires » pourra faire penser à celle des « nombres triangulaires ». A une différence près toutefois, qui est capitale. Dans la présente approche, il n'y a rigoureusement aucune signification à énoncer que « les premiers nombres triangulaires sont : 1, 3, 6, 10... ». En effet, quand on ajoute le segment (oo) au point (o), on ne reconstitue en rien un objet. La valeur du premier triangle cellulaire est donc évidemment 3, et comme tel il constitue un élément insécable (en deçà de quoi il n'existe tout simplement pas de triangle), et ses compléments correspondent à la série des nombres entiers supérieurs à 2.
La présente classification étant entièrement gouvernée par le paradigme logique de la reconstitution d'objets, il est évidemment essentiel que les éléments premiers et insécables à reconstituer soient définis de la façon la plus rigoureuse. Au risque de paraître un peu trivial, on émettra cette pure évidence logique : pour qu'un objet puisse être reconstitué, il faut d'abord qu'il ait été constitué; les mots "constitué" et "reconstitué" correspondant sans coup férir, pour chaque objet de notre tableau, aux deux premières valeurs stipulées dans leur formule entre parenthèses, - ce couple suffisant par là-même à les définir.
En mathématique pythagoricienne, un objet se caractérise précisément par sa capacité distinctive à être reconstitué (inclus le cas limite où cette opération le laisse inchangé); capacité qui le manifeste en tant qu'individu, et le libère, ou si l'on peut dire, le détache, "une fois pour toutes les autres fois", de la chaîne des autres objets auxquels il est génétiquement apparenté. Dans cette conception, un objet ne peut être correctement défini sans qu'aient été produits avec lui, sur un même rameau, d'autres objets, membres d'une même famille; et l'on peut raisonnablement penser qu'il n'existe pas d'autre manière de procéder.
*
S'il restait des lecteurs convaincus qu'il est mathématiquement intelligent de procéder à la manière du nombre figuré, en commençant toutes les séries d'objets par le nombre 1, nous leur répondrons que ce n'est pas intelligent, mais que c'est, au mieux, tautologique, et au pire, faux, selon l'interprétation qui peut être donnée de cette représentation. En effet, si l'on commence toutes les séries par le nombre 1, on est aussitôt contraint de constater que les nombres importants, dans chaque série, sont le deuxième et le troisième. Commencer toutes les séries par le nombre 1 équivaut donc à proférer une tautologie du genre : "S'il existe des séries telles que : (2, 3, 4, ...), (3, 6, 10, ...), c'est parce qu'il existe aussi un nombre appelé 1 qui ne comporte qu'une seule petite boule." En raisonnant ainsi, on commet une grave erreur logique, qui est de confondre la constitution des objets avec celle du système.
Enfin, lorsque, selon une autre interprétation, ce n'est pas tautologique, c'est tout simplement faux. Car il est faux de dire qu'une petite boule est à la fois un triangle, un carré, un cuboctaèdre, et une chaise. Ce paradoxe du point qui est tout et rien, propre à la théorie du nombre figuré, avait, du reste, interpellé nombre d'observateurs; - et l'on peut estimer qu'il est impossible de le résoudre correctement, sans recourir à l'analyse quadridimensionnelle.
*
On remarque que les polygones élémentaires se reconstituent au moyen de structures bien distinctes. Le triangle cellulaire se reconstitue au moyen de segments, le carré se reconstitue au moyen d'équerres, et l'hexagone se reconstitue au moyen d'anneaux hexagonaux. Il est naturel que la complexité du complément croisse en même temps que celle de la figure à reconstituer.
Il découle des remarques qui précèdent que, de la même manière que le côté d'un polygone cellulaire ne peut pas être inférieur à 2, l'arête d'un polyèdre cellulaire ne peut pas être inférieure à 2. Suivant ce principe, il s'avère aisé de déterminer le rang d'un polyèdre cellulaire quelconque, en comptant le nombre de cellules situées sur son arête. Par exemple, le cuboctaèdre d'arête 11 figurant dans notre tableau est le cuboctaèdre de rang 10, le tétraèdre d'arête 7 est le tétraèdre de rang 6, etc.
QUELQUES REMARQUES
Pavages polygonaux : principe général
Tout polygone cellulaire, triangle, carré ou hexagone, de quelque rang que ce soit, peut être pris comme élément de base pour former un pavage d'échelle spécifique. Toutefois, seuls les pavages carrés sont gnomoniques au sens restrictif qui nous est habituel ; c'est à dire qu'ils reconstituent la structure de l'élément de base par des solutions entières ; les pavages triangulaires et hexagonaux (construits, précisons-le, sur le même réseau cellulaire) nécessitant l'apport de compléments cellulaires, ces compléments étant eux même régis par des règles arithmétiques constantes.
Les pavages cellulaires hexagonaux présentent des propriétés arithmétiques intéressantes, en particulier à certaines échelles.
Pavages hexagonaux
La série des hexagones cellulaires correspond, dans la nomenclature des « nombres figurés », à la série des nombres hexagonaux centrés (1, 7, 19, 37, ...) ; à la réserve que nous avons déjà émise pour le triangle cellulaire, savoir : que la valeur atomique du premier hexagone cellulaire est évidemment 7, et non 1.

nombre hexagonal centré
On remarque que la série des hexagones cellulaires est identique à celle des gnomons du cube.
Pour former, à partir de n'importe quel hexagone cellulaire, un pavage d'échelle spécifique, on procède de la même manière qu'avec de simples cellules : on commence par disposer 6 pavés hexagonaux autour d'un pavé central, puis 12 autour de ceux là, puis 18, et ainsi de suite, comme dans l'illustration ci-dessous ; cependant on remarque qu'à chaque étape, les côtés de l'hexagone ne sont pas nettement délimités, mais se présentent comme des lignes brisées ; il manque à l'hexagone un certain nombre de cellules pour être complet, qui doivent donc lui être ajoutées.

Si on appelle E l'échelle du pavé de départ (correspondant à un nombre hexagonal centré donné), le complément latéral requis pour compléter le grand hexagone, de premier ordre, est de taille : 6 x E x (E-1)
Par conséquent la taille totale sera :
Echelles
(1) 7 x 1 + 6 x 0 = 7
(2) 7 x 7 + 6 x 2 = 61
(3) 7 x 19 + 6 x 6 = 169
(4) 7 x 37 + 6 x 12 = 331
(5) 7 x 61 + 6 x 20 = 547
(6) 7 x 91 + 6 x 30 = 817
(7) 7 x 127 + 6 x 42 = 1141
Exemple ci-dessous avec un pavage formé de 7 pavés élémentaires de 61 cellules (échelle 5), que nous empruntons aux travaux de Jaime Vladimir Torres-Heredia Julca : le complément latéral est de 6 x 20 = 120, et le grand hexagone compte donc 547 cellules.

pavage de Torres-Heredia Julca
Cette structure peut également s'analyser comme la somme de 54 tétractys + les 7 points blancs au centre des hexagones 61.
Torres-Heredia Julca a montré qu'en faisant abstraction de l'hexagone central, aussi bien que des compléments latéraux, la structure de ce pavage pouvait être décomposée de la manière ci-dessous, en 6 x 60 + 6 (les 6 cellules blanches au centre des hexagones), et qu'à ce titre il fournissait une bonne approximation du cycle de l'année (6 x 61=366), dans laquelle les hexagones correspondent à des "bimestres". (On peut noter que notre actuel calendrier respecte, grosso modo, l'alternance entre mois de 30 et 31 jours, qui donne des bimestres de 61 jours).

Suivant une indication de Dom Néroman, Rémy Bayoud a suggéré que cette structure pouvait apporter un éclairage sur l'une des plus anciennes cosmologies pythagoriciennes connues, due à Pétron d'Himère, selon laquelle il existerait "183 mondes, disposés sur un triangle". En effet le nombre 183 s'obtient en repliant cette structure sur un axe de symétrie médian, et correspond alors à un "semestre" de l'année. Une méthode encore plus satisfaisante consiste à interpréter la structure comme un "sceau de Salomon", et à rabattre un triangle sur l'autre en le faisant pivoter de 180° sur le centre géométrique de la figure, puisqu'alors on se retrouve même avec "183 mondes" disposés sur un triangle équilatéral.
Mais le pavage d'échelle 5 est encore remarquable à un autre titre, c'est qu'il engendre, en progressant dans les ordres supérieurs, une série infinie de nombres premiers, correspondant aux phases de reconstitution du grand hexagone. En effet, comme les nombres 61 et 547, les valeurs suivantes du grand hexagone sont toutes des nombres premiers et s'enchaînent avec la régularité parfaite qui peut être attendue dans un problème de pavage.

Cuboctaèdre cellulaire et dodécaèdre rhombique

Le caractère remarquable du cuboctaèdre cellulaire, c'est qu'il peut être envisagé comme « le gnomon de la sphère »... autant dire de la monade.
L'empilement cuboctaédrique de 12 sphères autour d'une sphère centrale peut légitimement être comparé, sur le plan logique, à l'empilement, dans un cube gnomonique de rang 3, de 26 petits cubes autour d'un cube central.
Les deux structures correspondent à une situation de « remplissage optimal de l'espace » autour d'une structure de base.
Précisons que, pour la sphère, cette conjecture sur le « remplissage optimal », considérée depuis longtemps comme certaine, n'a en fait été complètement démontrée que très récemment, en 2014.
Projeté sur un plan "équatorial", le cuboctaèdre correspond à la figure d'un sceau de Salomon inscrit dans un hexagone, structure particulièrement élégante, analogue à celle que l'on peut distinguer dans l'illustration ci-dessous.

Les 12 sommets des figures peuvent être mis en correspondance avec le dodécagone de nos horloges, comme une illustration parmi d'autres de la naturalité des divisions de temps que nous utilisons.
On peut remarquer au passage que cette structure présente une parenté intéressante avec le graphe associé au fameux « solide de Dürer », lui aussi à base « dodéca-cellulaire ».


En version classique, ou « non cellulaire », le polyèdre dual du cuboctaèdre est le dodécaèdre rhombique, formé de 12 losanges, polyèdre lui-même remarquable en ce qu'il est, avec le cube, le seul polyèdre convexe à remplir à lui seul l'espace.


Et on peut encore noter que c'est ce même dodécaèdre rhombique - du moins, sa moitié - qui sert aux abeilles à délimiter le fond de leurs galeries hexagonales, bien qu'il ait été démontré qu'il ne constituait pas (comme on l'a un temps supposé) la formule « la plus économique en cire », puisqu'il existait au moins une solution plus économique...

alvéole d'abeille à base hexagonale et à fond rhombique
Les diagrammes de Voronoï
Les diagrammes de Voronoï sont des structures logiques qui, à tout nuage de points du plan (appelés « germes »), répartis par hypothèse aléatoirement, associent une solution unique de pavage du plan par des polygones (« normalement » irréguliers). Pour les construire, rien de plus simple, on trace les médiatrices entre chaque point et ses voisins les plus proches, et on les interrompt... à l'endroit précis où elles rencontrent une autre médiatrice.

Comme la théorie des pavages cellulaires concerne précisément une série de problèmes qui se situent à l'interface entre la juxtaposition de cellules, d'une part, et la construction de pavages polygonaux ou polyédraux, de l'autre, les diagrammes de Voronoï ont, dans cette théorie, une valeur descriptive évidente. A ceci près que les réseaux cellulaires présentent, dans leurs diagrammes de Voronoï, une parfaite régularité qui n'est pas habituelle.
Il existe deux types de diagrammes de Voronoï pouvant être associés aux réseaux cellulaires, d'intérêt inégal : les diagrammes sphériques qui résultent de la projection de structures polyèdriques sur la sphère, et donnent une vision extérieure et en quelque sorte panoramique des réseaux cellulaires, et les diagrammes squelettiques, qui résultent, quant à eux, de l'analyse du réseau par des « coupes » bidimensionnelles transversales
Les diagrammes sphériques sont régis par la Loi de Bodart (que nous devons à une remarque de notre regretté ami Steven Bodart) :
Projeté sur la sphère, le dual d'un polyèdre cellulaire est son diagramme de Voronoï.
A partir de cette loi, toute solution de pavage cellulaire polyèdral de l'espace en 3 D peut être transformée en une solution de pavage de la sphère avec des tessons réguliers.
Par exemple, le dual du cuboctaèdre étant le dodécaèdre rhombique, au cuboctaèdre cellulaire élémentaire formé de 12 cellules groupées autour d'une treizième, correspond une solution de pavage de la sphère au moyen de 12 tessons en formes de losanges ; et ainsi des autres polyèdres cellulaires... - la remarque n'ayant, il est vrai, qu'un intérêt modeste, hormis peut-être esthétique.

Plus intéressants sans doute sont les diagrammes squelettiques, que nous nous contenterons d'introduire ici par un exemple « canonique », et qui « analysent », quant à eux la structure profonde d'un réseau cellulaire quelconque par des coupes bidimensionnelles transversales.
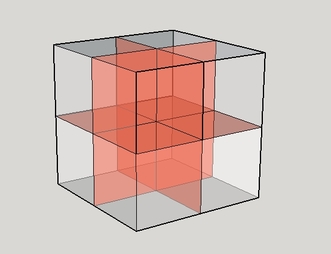
Diagramme de Barazzetti
Si, dans un cube gnomonique de rang 2, on enlève l'ensemble de la surface extérieure pour ne laisser subsister que le squelette, ou la structure intérieure, (en rouge dans l'illustration ci-dessus), on obtient un diagramme de Barazzetti, structure qui, dans sa version euclidienne la plus simple, se présente sous la forme de trois plans sécants, centrés et orthogonaux entre eux, dont la jonction délimite 12 plans carrés identiques, (ou encore : trois carrés gnomoniques de rang 2).

diagramme de Barazzetti
Dans un cube gnomonique "discret" composé de 8 petits cubes détachables, les 12 plans du diagramme de Barazzetti correspondent aux zones de contact entre ces cubes.

A présent, si l'on examine à nouveau la structure du cuboctaèdre cellulaire (12 sphères groupées autour d'une sphère centrale) on s'aperçoit qu'il est possible de la construire de plusieurs manières différentes par des assemblages de polygones cellulaires. L'une des solutions les plus évidentes consiste, comme on l'a vu, à la décomposer en un hexagone « équatorial », complété à ses deux pôles par deux triangles, orientés l'un par rapport à l'autre, dans la position des deux triangles opposés du sceau de Salomon.

Mais une autre solution consiste à construire le cuboctaèdre au moyen de trois carrés cellulaires entrecroisés, que notre illustrateur de hasard a eu la magnanimité de distinguer ci-dessous par 3 couleurs différentes : bleu, blanc, rouge. Or que remarque-t-on dans cette configuration? Les 12 cellules du cuboctaèdre correspondent aux centres des 12 carrés du diagramme de Barazzetti. Autrement dit : le diagramme de Barazzetti n'est autre que le diagramme squelettique du cuboctaèdre.


En effet, si l'on transforme les disques colorés du diagramme ci-dessous en des sphères de même diamètre et de même centre qu'eux, on retrouve les 12 cellules du cuboctaèdre.
Ce couple de structures remarquables : le cuboctaèdre cellulaire qui remplit optimalement l'espace avec de petites sphères, et son dual le dodécaèdre rhombique, qui remplit l'espace, « sort » donc immédiatement de la structure profonde du cube gnomonique de rang 2.
On nous permettra peut-être, pour l'occasion, de définir de manière volontairement un peu large le SQUELETTE LOGIQUE d'une structure quelconque, comme la partie de cette structure qui, amputée du reste, en conserve néanmoins les propriétés, ou le contenu mathématique essentiel.
Cette définition posée, on pourra remarquer que, de la même manière que le diagramme de Barazzetti est le squelette logique du cube gnomonique de rang 2, les 12 cellules du cuboctaèdre cellulaire sont le squelette logique du diagramme de Barazzetti.
Observation qui, rétrospectivement, semble justifier notre présupposé de départ, selon lequel les problèmes d'empilement compact et les problèmes de tessellation du plan ou de l'espace par des polygones ou polyèdres, gagnaient à être traités solidairement et d'une seule venue.
Les lois du gnomon sont une illustration de cette « corrélation ». On a vu dans d'autres articles que tout triangle gnomonique se transformait en carré gnomonique par une rotation de 180° des cellules monadiques qui sont ses triangles « pointe en bas », suivie d'une modification de 30° du paramètre angulaire ; logique dans laquelle les polygones atomiques, ou élémentaires, sont considérés comme des cellules souples, qui se « solidifient », ou se résolvent en différents « diagrammes de Voronoï », en fonction des positions relatives de leurs centres à tout instant du processus.

Dans cette représentation, l'état cellulaire correspond donc à une phase intermédiaire, ou de transition, entre différents systèmes de pavage polygonaux ; et de ce fait il apparaît comme plus fondamental, ou plus originaire ; - à l'image du paradigme cristallin, où ce sont des arrangements de "points" microscopiques, les atomes, qui par leur répétition, produisent à grande échelle des arêtes et des angles parfaitement "clivables", délimitant de parfaits polyèdres.
CONCLUSIONS
Quelques esprits froids pourront nous objecter que, par ces détours, nous n'avons fait que redécouvrir l'eau tiède de ce qu'est « un réseau cubique à faces centrées » . Tout bien réfléchi, nous nous en contentons. Dans un domaine aussi balisé que celui de la symétrie, il n'était pas question d'apporter ici ce qu'on entend par des « nouveautés mathématiques » ; il nous suffit que, chemin faisant, cette étude ait pu contribuer à apporter un peu d'ordre dans la formulation d'un problème logico-mathématique assez général, celui de la reproduction d'objet, où il n'en existait aucun... - symptôme d'une tendance de l'esprit mathématique, qui, à force d'habitudes généralisatrices, en est peut-être venue à être saisie d'un doute sur l'existence même d'objets mathématiques...
L'intérêt de l'approche quadridimensionnelle pythagoricienne réside, croyons-nous, dans le contraste entre la richesse des contenus de science que l'on est conduit à développer pour une compréhension suffisante des notions engagées, et l'étonnante simplicité de l'appareil logique grâce auquel on y parvient ; - puisque l'ensemble de ces structures mathématiques relativement complexes est construit ici, rappelons-le, au moyen d'objets tels que celui-ci :

29 MAI 2016
ANNEXES
I
Comment calculer facilement le rang et la valeur d'un polyèdre cellulaire d'après son aspect extérieur, et comment déterminer la valeur du polyèdre supérieur à un polyèdre donné.
On a vu que le rang d'un objet cellulaire quelconque se calculait par un moyen très simple : côté -1 pour les polygones, arête -1 pour les polyèdres. Quelques recettes permettent ensuite d'en déduire le nombre total de cellules, pour tout polyèdre.
Tétraèdre.
Le tétraèdre élémentaire, formé de quatre cellules, se reconstitue par l'ajout, à sa base, de triangles cellulaires, dont la progression correspond à celle des nombres triangulaires supérieurs à trois : 6, 10, 15...
Cube.
La série des cubes cellulaires est construite sur le même modèle que celle des cubes gnomoniques - à la réserve qu'elle débute avec un rang de décalage - puisqu'elle correspond à la série des cubes des nombres entiers naturels supérieurs à 1 : (8, 27, 64, 125....)
Octaèdre.
Tout octaèdre a pour plan de symétrie un carré cellulaire. Pour construire l'octaèdre de rang supérieur, on ajoute à l'octaèdre de base : ce même carré cellulaire + le carré cellulaire de rang supérieur.
Par exemple, l'octaèdre atomique, composé de 6 cellules, a pour plan de symétrie un carré cellulaire de 4 cellules. Pour construire l'octaèdre supérieur, on lui ajoute un carré de 4 cellules + le carré de rang supérieur, composé de 9 cellules. L'octaèdre de rang 2 se compose donc de : 6 + 4 + 9 = 19 cellules.
Cuboctaèdre.
Pour le cuboctaèdre, c'est à peine plus compliqué. L'illustration ci-dessous indique la série des compléments qui doivent être ajoutés au cuboctaèdre de base, composé de 13 cellules, dont on voit qu'ils suivent la progression : (42, 42 + 50, 42 + 50 + 70, 42 + 50 + 70 + 90...) et ainsi de suite.

II
Le vecteur d'équilibre de Buckminster Fuller
Richard Buckminster Fuller a attribué au cuboctaèdre divers noms tels que "vector equilibrium", "heléfantaèdre" ou "dymaxion".
Le cuboctaèdre est le seul polyèdre semi-régulier dont la distance du centre de gravité aux sommets est égale aux arêtes. On a donc au total 36 vecteurs isométriques, 12 pointant du centre aux sommets, en relation angulaire constante (60° partout), et 24 correspondant aux arêtes. Ce nombre s'élevant même à 72, si l'on prend en compte les vecteurs opposés.
Si ces propriétés sont bien connues, Buckminster Fuller est le premier à avoir saisi leur profond intérêt physique.
Cette situation d'équilibre vectoriel parfait peut être comparé à celle d'une bulle de savon en train d'être gonflée. La bulle tend à conserver sa forme sphérique à quelque échelle que ce soit : ici en raison de la tension de surface. Dans le cuboctaèdre, la croissance d'un vecteur pointant du centre à l'un des sommets, (égal au rayon de la sphère circonscrite), détermine la croissance isométrique et simultanée des 35 autres rayons et arêtes qui constituent avec lui l'ensemble de la structure, laquelle peut ainsi augmenter de façon continue "sans que rien ne semble se passer". Dans les deux situations, l'équilibre est parfait, parce que la tension est égale en tout lieu.
Buckminster Fuller compare cette situation à deux réalités qu'il est très important de comprendre dans un sens pleinement physique, si l'on ne veut pas s'égarer dans des interprétations poétiques : le silence, d'une part (où l'équilibre énergétique parfait est assimilé à l'absence totale de résonance); et le vide d'autre part, au sens d'une pure "virtualité" d'espace, non encore déterminée, ou encore, au sens d'un atome ou d'un grain d'espace.
"Le Vector Equilibrium est le point zéro de départ pour tout événement ou non-événement : c'est le théâtre vide et le cirque vide et l'Univers vide qui est prêt à montrer n'importe quelle action à n'importe quel public". (R. Buckminster Fuller)
De fait, les propriétés de ce "vecteur d'équilibre", formé de la somme nulle de 72 vecteurs, s'apparentent à celles du point "euclidien" sans dimension, dépourvu de métrique, qui n'a en soi de réalité que comme condition d'existence (et plus précisément : condition aux limites ou au bord) d'un hypothétique objet géométrique, resté lui-même non défini, ou à définir.
III
Cosmologie de Pétron et Lambda de Platon
On a vu que le pavage hexagonal d'échelle 5 imaginé par Torres-Heredia Julca fournissait une explication très séduisante des "183 mondes, disposés sur un triangle" évoqués dans la cosmologie de Pétron d'Himère.
A partir des "183 mondes disposés sur un triangle", correspondant dans cette hypothèse au Cosmos de Pétron, on obtient, par "dupli-rotation" (duplication + rotation de 180° de l'élément dupliqué), la structure en sceau de Salomon formée de "366 monades, disposées sur un hexagone", qui correspond quant à elle à l'Année dans le pavage de Torres-Heredia Julca :

On a remarqué aussi que ce pavage d'échelle 5, muni de ses compléments latéraux, pouvait s'analyser comme la somme de 54 tétractys + les 7 points générateurs au centre des hexagones 61. Ces nombres 54 et 7 ne peuvent manquer de nous faire penser au Lambda de Platon, structure formée de 7 nombres, dont la somme égale 54.
Cette coïncidence pourrait suggérer la possibilité d'une origine commune aux cosmologies de Pétron et de Timée; sinon même, l'hypothèse que toutes deux ne soient que les résidus d'un même ensemble théorique originel, plus complet.


On va voir que ce rapprochement peut être poussé un peu plus loin.
En effet, si l'on additionne les nombres du Lambda dans l'ordre naturel, on constate qu'ils se répartissent en trois sous-ensembles, dont la somme est à chaque fois un multiple de 6.
54 = (1+2+3) + (4+8) + (9+27)
Or ces différentes sommes inférieures correspondent, par une coïncidence assez remarquable, à trois régions, trois ensembles topologiques distincts du pavage hexagonal :
(1+2+3) = 6 = les 6 tétractys blanches qui composent l'hexagone central
(4+8) = 12 = les 12 tétractys blanches qui composent les "compléments latéraux"
(9+27) = 36 = les 36 tétractys colorées qui correspondent au "calendrier annuel"
Envisagé sous cet angle, le Lambda de Platon semble donc fournir un formulaire arithmétique pour la construction, comme pour la description du pavage; mieux, il paraît même contenir une recommandation implicite sur les différences de couleur à exprimer.
IV
Vues cavalières
La collection de manuscrits ésotériques de Manly Palmer Hall (1500-1825) conserve deux dessins représentant des diagrammes de Barazzetti en perspective cavalière, vus suivant la diagonale du cube gnomonique associé, de manière à former des "sceaux de Salomon". La même idée est illustrée avec des diagrammes de types "plein" et "vide".


Le dessin de gauche présente, en son milieu, une figure composée de trois losanges "vesica piscis" (formés de deux triangles équilatéraux), compris dans un hexagone : figure qui, en perspective, présente elle aussi une "ambivalence" du même genre, puisqu'elle peut être vue soit comme un cube, soit comme un dodécaèdre rhombique. "Le dodécaèdre rhombique pose des problèmes de vision dans l'espace, car lorsqu'on le regarde suivant une diagonale, on a l'impression de voir un cube." (Robert Ferréol, Mathcurve).
Dans le dessin de droite, on remarque que le sceau de Salomon lui-même peut s'analyser comme la superposition de trois losanges "vesica piscis", disposés en étoile.
(R. B, G. D)
V
Les objets cellulaires en équations
par R. Bayoud
J'appelle "coeur" le point central de rang 0 (hors-jeu si tu veux), autrement dit c(0) = 1
J'ai ensuite calculé le nombre d'éléments pour chaque "couche" c(n)
"figure(n)" correspond au total des éléments depuis le coeur jusqu'à la couche n : somme de 0 à n des c(k)
point(n) = 1
segment(n) = 1 + n
triangle(n) = ( 2 + 3n + n² ) / 2
carré(n) = 1 + 2n + n²
hexa(n) = 1 + 3n + 3n²
cube(n) = ( 2 + 3n + 3n² + 2n³ ) / 2
tetra(n) = ( 12 + 22n + 12n² + 2n³ ) / 12
octa(n) = ( 3 + 7n + 6n² + 2n³ ) / 3
cuboc(n) = ( 6 + 22n + 30n² + 20n³ ) / 6
Voilà pour les formules particulières.
Le développement des polynômes (de 1 à 4 termes) correspond à la position des objets sur "l'échelle" quadridimensionnelle. Du coup : chaque figure peut être vue comme un accord musical, dont les intervalles sont réglés par son polynôme. (Et comme on prend des ratios ça élimine le problème du dénominateur des fractions.) Pour les solides où les polynômes sont de la forme : a + b.n + c.n^2 + d.n^3, on peut ainsi théoriquement construire les intervalles : b:a, c:b et d:c, les 3 ensemble formant un "accord".
Quant à la formule génératrice de toutes les suites, elle me semble hors d'atteinte pour le moment.
La seule chose relativement évidente c'est qu'il s'agit d'un polynôme de coefficient fixe = 1 et de degré égal à la dimension impliquée.
REFERENCES :
Un lien géométrique entre le cercle et le système sexagésimal, Jaime Vladimir Torres-Heredia Julca, 2005.
La plaine de vérité, Dom Néroman, Arma Artis, 2009.
L'espace symbolique, Enrico Barazzetti, Archè, 1997.
Automates cellulaires et pavages vus comme des réseaux booléens, Hussein Ben-Azza, thèse de doctorat en informatique, sous la direction de Jacques Mazoyer, Lyon I, 1995.