-
La théorie générale du signe
LA THEORIE GENERALE DU SIGNE
par Guillaume Denom
à Antoine Abrassart
"The True" Scorpio Rising
Avertissement.
Le champ d'étude désigné dans cet article sous le nom de "théorie du signe" se distingue par deux traits essentiels. 1. Il envisage le signe en tant que réalité non seulement physique, mais véritablement matérielle. 2. Il présuppose que la mathématique est le champ approprié pour décrire la réalité définie en 1 sous le nom de signe. Ces deux traits, dans leur "restrictivité" même, empêchaient, comme on le comprend, d'utiliser les termes "sémiologie" ou "sémiotique", déjà associés à d'autres genres de réflexion sur le signe, ainsi qu'à d'autres définitions de ce concept.
Le tenseur binaire radical
Lorsqu'on la représente par la lettre V, la dyade indéterminée apparaît morphologiquement analogue au tenseur binaire radical de la linguistique guillaumienne, concept que cette théorie définit comme "l'opérateur universel de la structure du langage". La linguistique guillaumienne se distingue des autres écoles linguistiques par sa visée synthétique. Ce qui l'intéresse n'est pas, prioritairement, l'analyse architectonique du "système de la langue", mais un fait linguistique plus profond, agissant à chacun des niveaux de ce système, que son auteur qualifie de "psychomécanisme", ou, ailleurs, de "mécanisme de puissance de la pensée humaine". Il s'agit donc d'un opérateur antérieur à la problématique propre du langage et du signe, puisqu'il se rapporte, plus originairement, à la parole, en tant que geste et action entière de l'homme, non encore décomposée. Citons Gustave Guillaume :
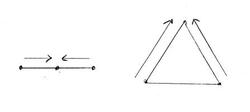
"La pensée tient sa puissance de ce qu'elle est habile à particulariser et à généraliser. Privée de cette double aptitude - qui constitue un entier (un entier intérieurement binaire) - la pensée serait sans force et inopérante. Or, si de ces deux opérations - particularisation et généralisation - desquelles la pensée tient sa puissance, on ne retient abstractivement que ce qu'elles comportent de mécanique, elles se réduisent à deux mouvements de pensée, l'un allant du large à l'étroit, (inhérent à la particularisation), l'autre allant de l'étroit au large (inhérent à la généralisation). Une réduction abstractive infléchie selon la pente arithmétique ramènerait la particularisation à un mouvement allant du plus au moins, et la généralisation à un mouvement allant du moins au plus. Le mécanisme de puissance de la pensée, c'est l'addition sans récurrence, sans retour en arrière, de deux tensions, une tension I fermante progressant du large à l'étroit, et une tension II ouvrante progressant de l'étroit au large, soit figurativement :
A ce mécanisme de puissance, on a, dans cet ouvrage, donné le nom pleinement justifié de tenseur binaire radical."
L'analogie entre ces deux notions : dyade indéterminée, et tenseur binaire radical, n'est en rien superficielle, mais, au contraire, tout ce qu'il y a de plus profonde; puisque ces deux notions constituent les fondements opposés, mais complémentaires, d'une discipline bipartite qui est la théorie générale du signe. Plus précisément, nous verrons que le tenseur binaire radical est à la théorie du signe linguistique, ce que la dyade indéterminée est à la théorie du signe mathématique, catégorie qui intègre, ici, une variété de systèmes de signes, tels que les systèmes d'orientation, les gammes musicales, ou les calendriers, dont la nature mathématique est comparable à celle des objets les plus fondamentaux produits par cette science, - tels que les nombres et les figures -, et dont le "substrat" ou le cadre transcendantal est le même, puisqu'il est celui des catégories universelles de l'espace et du temps. Et l'on s'apercevra qu'entre ces deux domaines ou ces deux visages du signe, le signe mathématique et le signe linguistique, la frontière, même si elle existe, n'est pas aussi épaisse - ni étanche - qu'on pourrait le penser de prime abord.
*
La théorie générale du signe est un point de vue depuis lequel on considère les systèmes de signes, ou encore, les paradigmes1, tels que, pour s'en tenir à un niveau élémentaire, les alphabets et les gammes musicales, comme formant eux-mêmes de "gros" signes unitaires et organiques, comme de pures singularités morphologiques. Dans cette théorie, on s'efforce d'appréhender d'un point de vue extérieur et équidistant, d'un côté, le nombre, à savoir, en l'espèce, des systèmes de signes, tels que les gammes musicales, qui sont issus de l'intuition d'une quantité mathématique discrète, et qui reposent donc sur un fondement stable et éternel, "a priori", sur un rapport intuitif et immédiat au même, à l'identité du nombre; et de l'autre, le verbe, ou le signe linguistique, dans toute sa naturalité, sa contingence initiale, son "instant d'arbitraire", qui fait qu'aucun nom, d'aucune langue, ne sait nommer les choses exactement dans la même "guise" qu'un autre. Or le tenseur binaire radical, dont l'ambition est de réduire le processus de la signification à un mécanisme universel, a précisément aussi la charge d'expliquer la genèse concrète, matérielle, du signe linguistique; et cet opérateur semble bien recéler cette capacité insigne, de savoir exhiber à la fois l'universalité, la constance, l'unicité du geste linguistique, et sa parfaite contingence ou déterminité naturelle, puisqu'il se distingue par ses applications spectaculaires à des faits de langue précis et localisés, tels que, par exemple, le système de l'article français, ou celui de la flexion nominale.
Le système phonologique des consonnes du français
Le tenseur binaire radical est efficient, pour commencer, dès le premier degré de la morphogenèse du langage, celui de la constitution du système phonologique, qui s'effectue par la transformation du continuum acoustico-vocalique de la phonation, en un champ d'unités discrètes : les phonèmes. Les tensions 1 et 2, "fermante" et "ouvrante", y jouent alors, très précisément, le rôle que jouent, dans le système morphogénétique de Turing, les fonctions chimiques, ou morphogènes, "inhibiteur" et "activateur", dont on sait qu'elles engendrent, en phases d'équilibre, des réseaux de gros points distribués en symétrie hexagonale; ce qui explique, comme nous allons tenter d'en exposer brièvement la raison profonde, l'omniprésence des structures hexagonales et des relations logiques biternaires dans la plupart des systèmes phonologiques.
structures de Turing, avec à gauche, phase d'équilibre hexagonal
La structure phonologique la plus caractéristique est une structure de type "sceau de Salomon", dans laquelle une relation ternaire faible, ou secondaire, est posée en tempérance d'une relation binaire forte, ou première. Sur un plan purement logique, la première différence constructive d'un système est, par définition, toujours binaire, mais il faut bien comprendre que le binaire est, fondamentalement, l'opérateur le plus impropre à la construction du continuum; ce que l'on peut illustrer sur le plan de la logique première, en remarquant que le segment, parce qu'il est la première différenciation de la monade, est aussi l'objet monadique qui ressemble le moins au point; et en effet les objets monadiques de rang 3 et 4, le disque et la boule, ressemblent plus au point que le segment. La relation ternaire joue donc le rôle de tempérance maximale de la relation binaire, - ou si l'on veut, de médiété - tempérance qui permet à une relation d'opposition binaire de se rapprocher le plus vite d'un envahissement général du continuum. Ainsi, dans le système phonologique des consonnes du français, les relations binaires fortes sont les relations "sourde/sonore" et "occlusive/fricative"; tandis que les relations ternaires se disposent en médiation (dentale/labiale/gutturale), ou en extension (nasale/liquide/semi-voyelle) de ces relations binaires fortes.
(Remarques.
I. Par souci de simplicité, les phonèmes sont ici désignés biunivoquement par des lettres de l'alphabet, qui, comme on le sait, sont souvent plurifonctionnelles. Pour être correctement interprétées, les lettres doivent être ici oralisées dans le paradigme "a";(1) c'est-à-dire que, pour connaître la valeur exacte des phonèmes du tableau ci-dessus, il suffit de faire suivre les lettres qui les désignent par la lettre "a"; ainsi, pour préciser les cas litigieux : "carte" et "garde" pour les occlusives "c" et "g", "wapiti" et "yak" pour les semi-voyelles "w" et "y", "chat" et "sable" pour les phonèmes "ch" et "s", "zazie" pour "z", etc.)
II. Contrairement à l'opinion de divers linguistes, aucun phonème du troisième niveau n'est inclus dans la classe "sonore". Même si nous avons pu constater que certains linguistes demeuraient réticents au principe autoritaire de la logique, la catégorie "ni sourde ni sonore" constitue pour nous une catégorie indispensable du système, pour une raison simple, qui est que la relation sourde/sonore constitue un ensemble biunivoque parfaitement compact. En effet, une sourde se transforme univoquement en la sonore correspondante par "sonorisation"; et réciproquement, cette sonore se retransforme univoquement en la sourde de départ par "assourdissement". La classe "ni sourde ni sonore" désignant dès lors, ni plus ni moins, l'ensemble des phonèmes qui sont exclus de cet ensemble biunivoque clos et complet. La catégorie phonologique "voisé - non voisé", qui implique une redistribution des trois classes : sourdes, sonores, ni... ni..., en deux classes seulement, n'a donc en français qu'une valeur descriptive, mais elle n'est pas pertinente pour l'analyse du système.
III. Ce tableau constitue, bien évidemment, un système complet des consonnes du français, définies selon la méthode jakobsonienne de permutation de la syllabe. Il recense donc l'ensemble fermé des 18 solutions "c" existant, en français, pour remplir une matrice de syllabe à deux éléments simples (c : Consonne / v : Voyelle).
Soit de ligne en ligne :
- table (T), partie (P), carte (C), sable (S), fable (F), chat (cH), pour les sourdes;
- dame (D), bac (B), gare (G), Zadig (Z), valise (V), jaloux (J), pour les sonores;
- navet (N), mare (M), rat (R), lac (L), wapiti (W), yak (Y), pour les ni sourdes ni sonores.
La lettre X, comme on le sait, ne correspond pas à un phonème, mais à 4 phonèmes différents, les deux sourdes de Félix (CS) et les deux sonores de Xavier (GZ); cette lettre signalant donc, par sa fonction comme par sa forme, le centre géométrique du paradigme sourd/sonore. La lettre K est un substitut phonologique de C. Enfin la consonne manquante de l'alphabet français, la fricative "ch" de "chat", est ici "représentée" par le graphème "inutile", non phonologique, de ce même alphabet : la lettre H; car, comme l'a indiqué Saussure, on ne peut en aucune manière appeler "phonème" un signe qui n'a d'autre existence phonétique, que le fait qu'on ne puisse faire, devant lui, ni liaison ni élision.
IV. Voyelles. Il n'existe pas de système constant des voyelles du français. Leur dénombrement même est impossible, étant sujet à des variations locales. Ainsi, les voyelles finales des mots "chacun" et "demain" correspondent à des phonèmes identiques à Paris, mais distincts à Toulouse. Pour les voyelles des mots "chauve" et "porte", c'est l'inverse : elles correspondent à des phonèmes identiques à Toulouse, mais distincts à Paris. Le français apparaît donc, à cet égard, moins différent qu'on pourrait le penser des langues sémitiques, dans lesquelles les voyelles sont réputées n'avoir pas d'existence véritablement individuelle. En revanche, le système des consonnes est rigoureusement constant, quelles que soient les différences d'accent ou de réalisation locales. Le phonème "r" peut-être roulé ou non selon les régions, il reste fonctionnellement un "r", c'est à dire qu'il conserve partout la même fonction dans le système.)
Si maintenant toutes ces relations biternaires sont déployées, ou libérées, non plus dans le champ logique bidimensionnel qui est celui d'un tableau analytique, mais dans un espace de diffusion "théorique" tridimensionnel, on s'aperçoit qu'elles se solidifient spontanément en un prisme hexagonal. Pour passer d'une structure à l'autre, il suffit d'enrouler le plan du tableau ci-dessus, en mettant bout à bout ses côtés gauche et droit.
Ce que l'on pourrait commenter ainsi : les relations logiques biternaires de type "sceau de Salomon" constituent l'opérateur de différenciation le plus rapide et le plus efficace pour transformer un "segment" (c'est-à-dire une relation d'opposition binaire) en un "disque" (hexagone), puis en un "cylindre" (prisme); ou encore, pour permettre à cette relation d'opposition d'envahir l'espace à trois dimensions.(2)
Pour que le modèle mécanique guillaumien soit opérant, il faut donc considérer que la tension 2, la tension ouvrante, est la tension binaire, ou "paire", tandis que la tension 1, la tension fermante, est la tension ternaire, ou "impaire". En effet, le ternaire étant toujours polarisé par un centre de symétrie qui est structurellement son origine, (centre correspondant ici aux catégories "labiale" d'une part, et "liquide" d'autre part) une tension ternaire peut être "fermante", ou "inhibitrice", lorsqu'elle est, géométriquement, une tension de contraction du segment (2) vers le point qui est son centre (1); ou bien, si l'on raisonne sur un triangle, une tension de contraction de ce triangle, régressant géométriquement de l'un de ses côtés (2), vers le sommet opposé (1).
La structure complète du système des consonnes pouvant dès lors se déployer en trois coups de temps seulement, trois entiers guillaumiens, ou trois "guillaume" correspondants aux trois étages de la structure ci-dessus; car nous attachons pour notre part le plus grand prix à cette propriété du tenseur binaire radical, un peu négligée par les guillaumiens et peut-être par G. G. lui-même, de permettre une expression quantifiée, et en ce sens véritablement scientifique, de la différence énergético-informationnelle dans laquelle consiste ultimement le signe. Notons que ce modèle apparaît en tout point conforme au formalisme logique de la dyade indéterminée, dans lequel l'impair, le fermé, précède toujours le pair, l'ouvert.
Notons que l'ensemble du système peut, à son tour, faire l'objet d'une résolution ternaire "fermante", ou "inhibitrice", analogue à celles qui opèrent à chacun de ses étages (au prix de l'ajout, dans le décompte des temps du système, d'un temps de genèse supplémentaire, logiquement antérieur aux trois moments dénombrés ci-dessus, et qui correspond, comme on le verra plus loin, au moment "zéro" de la théorie pythagoricienne du signe, qui est celui de la coordination du système avec lui-même); à cette réserve près que, dans une telle application, c'est l'étage inférieur, le "ni-ni", qui devrait plutôt occuper la position centrale, et donc le niveau médian de la structure, puisque ce connecteur logique correspond bien réellement, ici, au pôle de l'imparité et de la fermeture, qui, selon le formalisme de la dyade indéterminée, s'oppose à la parité et à l'ouvert de l'ensemble biunivoque "sourdes et sonores".(3) Précisons que la disposition adoptée dans les figures ci-dessus résulte uniquement de la contrainte bidimensionnelle de la logique de tableau (logonique), adoptée ici par simple commodité et en raison de sa richesse analytique. Mais la représentation suggérée dans le présent paragraphe apparaît préférable d'un point de vue synthétique, en ce qu'elle permet d'exprimer le système, non plus sous la forme du quasi-cylindre (prisme), mais sous celle du sphéroïde ou de la quasi-boule topologique, en assignant à l'ensemble hexagonal "ni-ni" la fonction topologique d'un disque équatorial, et aux ensembles "sourdes" et "sonores" celle, logiquement seconde, de disques tropicaux, respectivement nord et sud. Or la représentation sphérique, en raison de sa nature monadique, correspond, comme on le verra plus loin, à l'expression mathématique optimale du processus d'envahissement constructif du continuum perceptif, dans lequel consiste toute la nature du signe linguistique matériel.
*
Le choix, par Gustave Guillaume, d'un modèle mécanique, plutôt qu'un modèle chimique ou autre, est, à lui seul, assez lourd de conséquence. Il peut se réclamer d'un certain principe d'économie scientifique, qui est celui du "moindre besoin". La science trouve toujours meilleur ce qui est fait avec des moyens plus "rustiques", lorsque ceux-ci s'avèrent suffisants. Mais surtout, le choix d'un modèle mécanique a pour effet de placer, par hypothèse, l'organe du langage - ou si l'on veut, son centre organisateur - beaucoup plus près du corps et de son activité mécanique, sinon musculaire, que du cerveau, et de son activité chimique ou électrique.
*
Ces deux notions, dyade indéterminée et tenseur binaire radical, nous représentent donc les deux visages, ou les deux côtés du signe; un côté qui implique, originairement, passivité, prudence, patience ou réceptivité, (la tétractys, par exemple, est essentiellement un "récipient", ou un "réceptacle", pour reprendre la terminologie technique du Timée), et qui est tourné vers ce qui est stable, constant, et éternellement le même, vers le nombre; et un autre côté qui consiste, originairement, en une action, en un engagement en quelque sorte libre, souverain, ou créateur, dans la matière, avec tout ce que cela comporte de "hasard heureux" et de "chatoiement" poétique de l'être, et qui est la parole, en tant que geste et action générique de l'homme. La connaissance pythagoricienne n'étant qu'un accord, ou une harmonie, entre cette naturalité et cette éternité. Car ces deux côtés du signe ne peuvent jamais, en effet, être séparés complètement l'un de l'autre, puisque même le nombre, pour être reçu, doit d'abord être saisi par l'entremise d'un nom. Inversement, on a vu, avec Gustave Guillaume, que l'opérateur le plus profond de la langue se réduisait, en définitive, à un infléchissement arithmétique, à une espèce de tendance à "imiter" le nombre.
Systèmes d'orientation, gammes et calendriers
A la famille des systèmes "mathématiques" appartiennent, outre les gammes musicales, les systèmes relevant du paramétrage de l'espace temps, tels que les systèmes d'orientation et les calendriers. Les problèmes de "comma" musical sont, mathématiquement, analogues à ceux posés par le comput calendaire. La tendance à une stabilisation hexagonale ou dodécagonale - en considérant que ces diverses divisions du temps peuvent être représentées par des divisions du cercle - demeure, néanmoins, assez générale à ces systèmes (gammes et calendriers). Le système babylonien, conservé par la civilisation moderne, est sexagésimal; l'année, comme le zodiaque, comme la journée, et comme l'heure de nos horloges, a 12 divisions; et notre système musical, après une computation interne de plus de deux mille ans, s'est stabilisé en une gamme tempérée de 12 demi-tons, soit 6 tons entiers.
Les couleurs
D'autres systèmes, enfin, appartiennent à une catégorie intermédiaire; ainsi, les systèmes de noms de couleurs internes à chaque langue naturelle qui, bien qu'ils relèvent de la contingence linguistique, réalisent, la plupart du temps, un paramétrage mathématique à peu près idéal, et quasi constant, du spectre de la couleur. Les mêmes "stations" se rencontrent, à quelques nuances près, dans la plupart des idiomes occidentaux, permettant une transmission relativement aisée, d'une langue à l'autre, de l'expérience de la couleur, pourtant incommunicable par nature, en l'absence d'un référent universel et non subjectif. "Les couleurs", en effet, n'existent pas, puisque la couleur est originairement un phénomène singulier, un continuum. Le bleu n'est, en soi, rien de plus que la somme des expériences et des idées humaines qui se sont accrochées au mot "bleu", depuis que ce mot est utilisé (comme le démontre suffisamment, par exemple, le fait qu'il corresponde à deux mots différents en langue russe). Le référent des couleurs que nous avons l'habitude de nommer comme des individus, n'a donc, en toute rigueur, aucune existence absolue en dehors des noms naturels qui en fixent la notion. Son concept ne se "substantialise" que par un va et vient à la vérité fort subtil, dans lequel entrent en jeu, simultanément : 1) la consistance topologique intrinsèque, originairement locale, du seul système de signes - le système des noms de couleurs - qui, par sa vertu propre d'opérateur de différenciation, détermine ces signes, dans leur usage, tantôt à s'attirer, tantôt à se fuir magnétiquement de proche en proche, par un mouvement devant normalement les conduire, dans leur devenir utilitaire, à se satelliser, (sur le continuum virtuel dont ces unités transportent le principe avec elles), à une distance étalon de valeur 1 les uns des autres; et 2) la confrontation permanente de ce même système avec l'expérience quotidienne, qui amène la notion de ces signes à "s'infuser" graduellement de réalité ou de substantialité empirique, par un mouvement de reconnaissance par "approches" - ou par une "approximation" perceptive;(4) - ces deux mouvements, pour finir, se soutenant et se guidant l'un l'autre. Dans la genèse concrète du système, on peut imaginer que ce dynamisme, ce mouvement "optimiste" de la signification, puisse commencer à s'activer à partir d'un graphe rudimentaire de, par exemple, 4 ou 5 unités, dont la structure ou la configuration définitive demeurerait, dans un premier temps, indécise, ou fluctuante; c'est à dire que l'on peut imaginer une langue primitive qui ne disposerait que de quatre ou cinq noms de couleurs. En revanche, nos systèmes modernes relèvent probablement d'un lent processus de "décantation" statistique, ou économique, de nature essentiellement pratique.
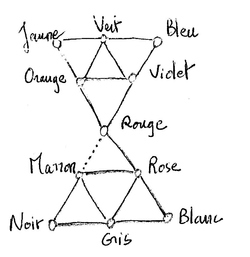
Structure "sablier" du paradigme français des noms de couleurs
Triangle "Mondrian".
Couleurs dites "primaires" (Rouge-Jaune-Bleu)
Triangle "Malévitch".
Couleurs dites "alchimiques" (Rouge-Noir-Blanc)
Chacun des "registres" du sablier enferme virtuellement une structure hexagonale biternaire de type "sceau de Salomon". En outre, la structure générale du sablier lui-même est topologiquement analogue à la structure "fermante-ouvrante" du tenseur binaire radical; de sorte que le système peut nous apparaître comme formant un "super-entier" guillaumien fermant-ouvrant, composé en réalité de deux entiers conjoints ou "siamois".
Ce paradigme linguistique est, par exemple, rigoureusement identique à celui de la langue anglaise, où les onze stations du sablier (brown, black, grey, white, pink, red, orange, yellow, green, blue, purple) correspondent, comme en français, aux onze noms de couleurs qui sont statistiquement les plus utilisés. De tels paradigmes peuvent être qualifiés d'"optimaux", en ce qu'ils réalisent un compromis parfait entre une variété de contraintes empiriques, voire expérimentales, dont les unes sont optiques, telles que le paramétrage des "couleurs de l'arc-en-ciel", ou, plus exactement, de l'expérience visuelle de la décomposition de la lumière (triangle supérieur), et les autres physico-chimiques, telles que la fabrication de nuances "intermédiaires", par le mélange de matières, ou de pigments colorés "primaires" ou fondamentaux (ensemble du paradigme).
La même structure peut être déployée sur un axe continu, par exemple un escalier, sur lequel les stations fortes arrivent une fois sur deux. Ainsi, si l'on part du noir, les 5 stations fondamentales sont les stations impaires.
En conclusion de cet aperçu sur la couleur, on peut remarquer que la relative impuissance des théories modernes de la couleur à cerner la véritable essence de cette dernière, résulte assez généralement de la conviction partagée (bien antérieure à la notion officielle - d'ailleurs falsifiée et infidèle à la véritable pensée de Saussure - d'arbitraire "pseudo-saussurien" du signe), que la couleur ne peut de toutes façons pas résider dans son nom, pour la raison que celui-ci ne peut être qu'un signe "arbitraire" ou "conventionnel", au sens assez banalement négatif et réducteur que peuvent revêtir ces deux expressions. Ce préjugé assez général a conduit les théoriciens modernes à chercher, tantôt à objectiver la couleur par quelque procédure expérimentale chimique ou optique, tantôt, à l'exemple de Goethe (5), à la résorber dans le registre subjectif de la pure sensibilité, sinon même de l'émotivité. Mais ce qui a échappé à tous, (y compris au pourtant très sagace Newton) c'est qu'une fois qu'on avait produit toutes ces "simulations" phénoménologiques de la couleur, on avait seulement montré les raisons de la couleur, ses motivations en quelque sorte externes et contingentes - mais toujours pas la couleur elle-même, dont le contenu possible était pourtant "connu" et déterminé depuis le début, puisqu'il résultait de la toute puissance productive, a priorique et en quelque manière magnétique, émanée de la seule hypostase originelle de son nom.
De la consistance logique continue de la théorie du signe matériel, à travers la nature mathématique diverse de ses principaux continuums de référence
Un témoin significatif des conceptions qui étaient celles des pythagoriciens, en matière de théorie du signe, est ce fameux passage du Protreptique d'Aristote, où l'on compare les trois doubles consonnes grecques formées à partir de la lettre sigma, avec les trois accords fondamentaux de l'harmonie musicale, rapportés à l'unisson. Cette comparaison à laquelle le malheureux Aristote ne comprend goutte, parce qu'il ne saisit pas le point de vue depuis lequel elle est énoncée, est d'une profonde pertinence théorique, comme on peut tenter, ici même, de l'exposer en quelques traits; et elle n'est pas le seul témoin du haut degré de technicité et de rigueur formelle qu'avaient acquis les spéculations des pythagoriciens, en matière de théorie du signe.
Mais avant d'entrer dans le coeur du problème, il convient d'évoquer certaines considérations générales concernant la théorie du signe, qui ne pouvaient être abordées avant que des exemples précis du genre de systèmes auquel cette théorie s'applique, fussent produits, ou extensivement définis.
En tout premier lieu, il convient de se défaire de l'idée que puisse exister, dans la théorie du signe, un plan phénoménologique correspondant à celui de la pure sensation, ou d'une réception sensorielle absolument passive, dénuée de toute intentionnalité, de toute dimension active, telle qu'en subsument, le plus souvent, les catégories rigides de la psychologie moderne, quelques diverses qu'elles puissent être.
Les différents continuums sur lesquels raisonne la théorie du signe matériel, ne sont pas à proprement parler des continuums sensoriels, mais bien plutôt perceptifs, c'est à dire qu'ils comportent tous un élément relevant d'une certaine "magnétisation" préalable, ou "intentionnelle" et par conséquent active de la sensibilité, transcendante à l'indéterminité purement "objective" du fait sensoriel. Cependant, ces continuums se distinguent entre eux par le fait de comporter, les uns par rapport aux autres, une plus ou moins forte proportion de réceptivité, de passivité, ou au contraire d'opérativité et d'activité.
De la même manière, le point commun aux différents systèmes que l'on a envisagés ici, est de consister, chaque fois, en une action organique de structuration d'un certain continuum perceptif, par la constitution d'un système d'unités discrètes régi par des interrelations logiques (elles-mêmes assimilables à autant de "logoi", ou de rapports d'entiers pythagoriciens); cependant, ces continuums ne comportent pas nécessairement le même nombre de dimensions mathématiques "théoriques", comme on peut aisément s'en rendre compte à l'usage. En effet.
Le continuum de la tonalité, abstraction faite de ses conditions de réalisation pratiques, peut être représenté par un axe mono-dimensionnel (dimension pythagoricienne 2),(6) comme il l'est dans la représentation courante du langage, où il est symbolisé par un axe appelé tantôt "haut-bas", tantôt "aigü-grave", expressions qui ont des sens assez voisins. Le continuum de la couleur, avec l'expression de ses différences combinatoires biternaires de type "sablier", requiert, quant à lui, au moins deux dimensions (dimension pythagoricienne 3); c'est-à-dire que, même si l'expérience de la couleur pourrait, en théorie pure, être communiquée à un sujet ne connaissant que l'existence de deux dimensions, elle nécessite au minimum cette capacité de percevoir un "écran", sur lequel puissent apparaître différentes "taches colorées". Enfin le continuum de la phonation se distingue à son tour de ces deux premiers exemples, en ce que sa définition ne procède pas d'une seule aire sensorielle (telle que l'"oreille" pour la musique, ou l'"oeil" pour la couleur, dans une acception anatomique volontairement vague de ces deux "organes" sensoriels) mais de l'interconnexion de deux aires sensorielles; car en effet, le continuum de la phonation n'est pas seulement vocalique, mais acoustico-vocalique, de sorte que, bien qu'il soit entièrement immergé dans le domaine de l'empirique et du perceptif, il résulte de la mise en correspondance de deux "aires" sensorielles antagonistes, l'une active, représentée par l'appareil phonatoire, l'autre passive, représentée par l'organe de réception des sons élaborés par ce dernier. C'est pourquoi les propriétés d'un système tels que celui des consonnes, ne peuvent complètement se déployer que dans une dimension théorique supérieure à celle du plan, par conséquent en dimension pythagoricienne 4.
Le continuum de la tonalité peut apparaître, à cet égard, comme le plus passif, en ce qu'il est indépendant des conditions concrètes de sa production, que celles-ci puissent être actives ou non n'ayant aucune incidence en la circonstance. La musique est en effet la réception d'un rapport arithmétique absolument pur et constant, dont la saisie ne nécessite aucun "geste" ni "exercice" musical particuliers, pas plus qu'elle n'exige la connaissance consciente des valeurs numériques correspondantes aux accords musicaux, puisqu'elle relève d'un registre empirique plus profond que ceux-là, que l'on peut légitimement qualifier de "subconscient" ou, si on préfère, de supra-conscient, qui est celui, tout naïf ou naturel, du sentiment immédiat de l'accord ou de l'harmonie, du "juste" et du "faux".
A l'inverse, le continuum acoustico-vocalique de la phonation est dépendant de la coordination préalable d'un appareil de production, avec un plan de réception antagoniste; et de ce fait, il intègre une plus forte proportion d'opérativité, d'activité, voire de "gestualité", dans sa constitution matérielle même, que le continuum tonal.
Ces divers points précisés, il paraît maintenant plus aisé de gloser le fragment pythagoricien du Protreptique d'Aristote.
La saisie pythagoricienne considère les trois doubles consonnes grecques formées à partir de la lettre sigma comme constituant hypothétiquement l'axe vertical polaire du système des consonnes; en considérant comme point zéro ou origine polaire de ce système, la lettre sigma elle-même en tant qu'elle n'est coordonnée à aucune autre. Puis il établit une correspondance entre ces trois modes de coordination de la lettre sigma, et ces trois rapports de coordination de la note tonique que sont respectivement la quarte, la quinte et l'octave. Soit :
0. Sigma - Ton
1. Ksi - Quarte
2. Psi - Quinte
3. Dzêta - Octave
On peut remarquer que les trois niveaux déployés ici correspondent, en grec comme en français, au ternaire fondamental des points d'articulation de la phonation : guttural - labial - dental; de sorte que le "retour" de la dentale originaire (sigma) dans le dernier rapport (la lettre dzêta étant une combinaison de deux dentales) se trouve correspondre, terme à terme, au retour cyclique, ou "hélicoïdal", de la position de l'origine (ton) dans le rapport d'octave. On peut ensuite remarquer qu'en français aussi, l'axe polaire du système des consonnes coïncide avec celui qui traverse les doubles consonnes formées à partir de la lettre S : savoir la double-sourde de Félix et la double-sonore de Xavier, même si le français ne possède pas d'autres doubles consonnes naturalisées dans l'alphabet, et si dans le système propre à cette langue, le ternaire le plus fondamental est un ternaire différent de celui des points d'articulation.
N'en déplaise à Aristote, une telle comparaison apparaît donc bien légitime, si on la considère, avec la méthode adéquate, sous l'angle scientifique particulier qui est celui de la théorie du signe, domaine, il est vrai, dont cet auteur assez peu mathématicien, ne soupçonnait probablement pas même la possibilité de l'existence.
(1) En sympathie, pour une fois, avec les variations de l'usage moderne à ce sujet, le terme "paradigme" désigne, synthétiquement, dans nos pages, comme il le faisait, il me semble, dans la pensée des anciens, à la fois l'exemple, et le système de coordonnées, ou encore l'ensemble, non nécessairement clos, dont cet exemple est un exemple; la consistance de notre travail permettant, chaque fois, de savoir dans quel sens il est utilisé. Pour employer une image, le terme paradigme désigne la roue d'un système, en tant qu'elle peut être représentée par chacun de ses rayons, ou mieux encore, en tant que la nature même d'une roue ne consiste, ou ne résulte, que de la possibilité qu'ont ses rayons de permuter, de prendre la place l'un de l'autre
(2) Pour être plus précis, la structure à trois étages du système phonologique des consonnes du français contient deux ensembles de structure biternaire, ou "sceau de Salomon" : l'ensemble "sourd" (t-p-c, s-f-ch) et l'ensemble "sonore" (d-b-g, z-v-j), et un ensemble de structure terbinaire, correspondant ici au rez-de-chaussée de la structure : l'ensemble "ni sourd ni sonore" (n-m, r-l, w-y).
(3) Dans notre article sur la construction pythagoricienne de la géométrie, en page 1 de ce blog, nous avons présenté le connecteur logique "et" (synthétique) comme un opérateur "entrant" ou "fermant", et son antagoniste, le connecteur "ni..., ni..." comme un opérateur "ouvrant". Pas de contradiction ici néanmoins. Le "et" dont il s'agit ici est bien le "et" analytique et ouvrant ("un homme et un chien se rendaient au marché"), auquel s'oppose, comme son complément, un "ni..., ni..." synthétique, et fermant, désignant un objet qui n'a aucune des deux propriétés en question, ou qui, à la rigueur, les possède "l'une et l'autre à la fois", sur le mode de l'indistinction. Pour des raisons naturelles, dont l'explication nous entraînerait trop loin, le système phonologique des consonnes utilise, précisément, les fonctions des connecteurs logiques au rebours de celles qui sont les leurs dans la logique prédicative.
(4) Cette notion d'approche, ou d'approximation perceptive peut, à première vue, apparaître paradoxale; mais elle ne l'est que si l'on ne considère la perception que comme un fait absolument passif, calqué sur la rigidité du schéma psychologique moderne : émetteur - récepteur, ce qu'elle ne peut être en aucune manière dans l'ordre phénoménologique qui est celui de la couleur; puisqu'on peut poser en principe qu'un sujet n'a, a priori, aucune chance particulière de rencontrer dans son champ de perception du vert, du rose, de l'orange, s'il n'a, auparavant, activé en quelque manière le "tenseur" ou "l'attracteur" capable de motiver et de guider une semblable "rencontre", et dont le foyer ne consiste que dans l'idée abstraite de la couleur, dans son concept même.
(5) Sachant que, comme l'a lucidement indiqué Wittgenstein, la "théorie des couleurs" de Goethe est un travail littéraire qui, quelle que soit sa valeur, ne contient aucune théorie scientifique de quelque nature que ce soit. En revanche sa querelle à l'encontre de Newton nous fait l'effet d'un chef d'oeuvre d'incompréhension, mais aussi de prévention imbécile contre ce qu'il s'imagine être "l'esprit mathématique"; préjugé d'autant plus regrettable de la part d'un auteur qui se voulait, avec sincérité sans doute, un philosophe de la nature.
(6) Précisons que nous ne parlons là que du continuum tonal absolument pur et a priori, indépendamment des systèmes d'unités discrètes que l'on peut définir à l'intérieur de lui; car, une fois mathématiquement qualifié, l'axe monodimensionnel de ce continuum devra nécessairement adopter la forme de l'hélice (ou de l'"escalier hélicoïdal"), afin d'exprimer la récurrence périodique des rapports harmoniques qu'il contient.
Décembre 2013
Référence :
Gustave Guillaume : Essai de mécanique intuitionnelle - t. 1, Espace et temps en pensée commune et dans les structures de langue, Presses de l'université Laval, Québec, 2007.