Annexe 1 : Solide de Dürer et pavages gnomoniques

SOLIDE DE DÜRER ET PAVAGES GNOMONIQUES

 

 

 

par Guillaume DENOM

 

 

 

 

 

 

 

 

 

 

 Chapitre 1

 

SOLIDE DE DÜRER ET RHOMBOEDRE ASSOCIE

 

 

 

 

 

Le solide de Dürer (pour les puristes : le trapèzoèdre triangulaire tronqué) est un rhomboèdre tronqué. Un rhomboèdre est un cube étiré sur l'une de ses grandes diagonales.

 

Les faces du rhomboèdre sont simplement des losanges au lieu d'être des carrés, mais le cube lui-même peut parfaitement être considéré comme un cas limite de rhomboèdre.

 

On peut construire un solide de Dürer à partir de n'importe quel rhomboèdre, en tronquant précisément les deux sommets opposés sur lesquels il est étiré. La forme du solide de Dürer dépendra donc de l'angle choisi pour le losange correspondant à la face du rhomboèdre. Certains cas sont particulièrement intéressants, en ce que le rapport des angles du losange s'exprime par de petits entiers. On peut en citer trois.

 

Le cube, pour lequel le rapport des angles du losange est de 90°/90° = 1/1 = 1.

 

Le rhomboèdre gnomonique, dans lequel le rapport des angles est de 60°/120° = ½

 

Le rhomboèdre d'or, dans lequel le rapport des angles est égal à 72°/108° = 2/3. Le solide de Dürer associé à ce rhomboèdre correspond à une situation d'équilibre parfait entre 2 possibilités d'orientation de l'angle du losange, l'une dans le sens obtus, vers le carré 1/1, l'autre dans le sens aigü, vers le losange 1/2, perfection qui se traduit par le fait que ses sommets sont inscriptibles dans une sphère; - le nombre d'or correspondant d'ailleurs généralement, dans l'ordre physique, à une semblable situation d'équilibre entre deux forces ou tendances antagonistes.

 

Les pythagoriciens fidèles à leur nonchaloir auront reconnu, dans ces trois cas particuliers, les trois rapports musicaux que sont l'unisson (1/1), l'octave (2/1) et la quinte (3/2), qui correspondent au développement en procession des trois premiers étages de la tétractys; ce ternaire constituant en l'espèce une structure fermée.

 

 

 

Notons que le solide représenté par Dürer dans sa gravure Melencolia ne se rapproche bien nettement d'aucun de ces trois types, puisque son angle apparent se situe aux environs de 79 ou 80°.

 

 

 

Le rhomboèdre gnomonique

 

On s'intéressera ici principalement au rhomboèdre gnomonique, d'angle 60°/120°, et à son solide de Dürer associé.

 

 

 Solide de Dürer gnomonique

 

 

Le solide ci-dessus se compose de 3 éléments, un octaèdre au centre, et deux tétraèdres tronqués, en haut et en bas. Il est naturellement plus étiré que celui de Dürer, mais on retrouve bien nos 6 faces pentagonales et nos deux faces triangulaires. Pour obtenir une expression gnomonique entière, il suffit de considérer les 3 éléments qui le composent comme des polyèdres gnomoniques de rang 2, semblables à ceux-ci :

 

 

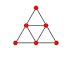
Tétraèdre et octaèdre gnomoniques de rang 2

 

 

Les tétraèdres gnomoniques devront simplement être diminués d'un petit tétraèdre, par exemple le rouge situé ici au sommet.

 

L'octaèdre central du solide de Dürer se décompose alors en 6 petits octaèdres + 8 tétraèdres, et les deux tétraèdres tronqués, pour chacun, en 1 octaèdre + 3 tétraèdres. Le solide de Dürer complet se composera donc de 8 octaèdres + 14 tétraèdres, soit 22 éléments en tout. Pour compléter ensuite le grand rhomboèdre, il faut encore ajouter un tétraèdre à chacun des sommets tronqués, de sorte que ce rhomboèdre présentera lui une composition bien équilibrée de 8 octaèdres pour 16 tétraèdres, soit 24 éléments en tout.

 

A la simple vue des polyèdres gnomoniques dont il se compose, on comprend que le solide de Dürer peut être construit à partir d'un patron composé uniquement de triangles équilatéraux. Chaque face pentagonale se décompose en effet en sept triangles équilatéraux; les six pentagones se subdivisent donc en 6x7=42 triangles équilatéraux, auxquels s'ajoutent 2 triangles pour fermer les troncatures ; soit au total 44 triangles équilatéraux. On remarque que ce nombre est le double de celui des petits solides utilisés pour la construction gnomonique du même polyèdre (22), où l'on découvre donc une nouvelle expression du rapport ½ qui traverse toute la structure.

 

 

La relation du solide de Dürer à son dual : une auto-dualité contractée

 

Le dual du solide de Dürer est un rhomboèdre semblable au grand rhomboèdre de départ, avant sa troncature, bien qu'évidemment d'une échelle différente. Il s'agit là d'une propriété très singulière, car, en raison de la "coplanarité" de certaines de ses faces (c'est à dire de leur appartenance à un même plan), le dual du solide de Dürer a la propriété spéciale de posséder moins de faces que le solide de Dürer n'a de sommets, précisément deux fois moins. En effet, l'ensemble de ces faces, triangulaires, fusionnent deux à deux pour former des losanges.

 

Dans les nomenclatures, le dual du solide de Dürer est référencé sous le nom de bipyramide triangulaire gyroallongée, et, en tant que dual d'un polyèdre à 12 sommets, il est fréquemment présenté comme un dodécaèdre. Toutefois, cette façon de le qualifier tient uniquement à la rigidité des définitions mathématiques, car, en réalité, ce n'est bel et bien qu'un banal rhomboèdre, doté de 6 faces seulement. Et on n'en trouvera sans doute pas de meilleure preuve que le fait qu'il soit exclu de la liste des solides de Johnson (avec ici des explications à l'appui) pour la raison précisément que ses faces - des losanges - ne sont pas des polygones réguliers.

 

 

Solide de Dürer et rhomboèdre dual inscrit

 

Il existe donc une forme d'auto-dualité entre le solide de Dürer et son rhomboèdre dual, mais une auto-dualité très particulière, qu'on pourra qualifier de "contractée". En effet, il existe une homothétie qui projette les sommets du rhomboèdre dual sur ceux du solide de Dürer, mais à l'exclusion de certains points. Autrement dit,  le solide de Dürer peut être vu comme une contraction de son dual, résultant de la projection de ce dual sur une partie de lui-même.

Cette opération de contraction est toutefois justiciable d'une définition mathématique très précise, en géométrie projective notamment, où elle constitue un groupe spécifique de transformations.

 

Le rhomboèdre dual inscrit pourra, naturellement, se décomposer en trois éléments semblables à ceux du grand rhomboèdre : un octaèdre et deux tétraèdres, évidemment non tronqués.

Pour le solide de Dürer gnomonique, la dimension du rhomboèdre inscrit est très facile à déterminer. En effet, pour construire le solide de Dürer, le grand rhomboèdre de départ a été tronqué d'un tiers de sa hauteur, (mesurée sur l'axe d'étirement commun au solide et à son dual, comme dans l'illustration ci-dessus).

Le rhomboèdre dual inscrit aura donc une hauteur égale à 2/3 de ce grand rhomboèdre. Par conséquent, si, par exemple, pour le grand rhomboèdre, on a utilisé un octaèdre et deux tétraèdres de 6 cm d'arête, alors, pour le dual inscrit, on devra utiliser un octaèdre et deux tétraèdres de 4 cm d'arête.

 

 

Une quadruple identité très remarquable

 

On a ici une quadruple identité très remarquable entre :

Le rapport des angles du losange (60°/120°) = la composition gnomonique du polyèdre dual (1 octaèdre / 2 tétraèdres) = la composition gnomonique du grand rhomboèdre détronqué (8 octaèdres / 16 tétraèdres) = enfin le rapport entre la composition du solide, et celle de la surface (22 éléments pour le solide / 44 triangles équilatéraux pour la surface), - ce dernier rapport se conservant d'ailleurs pour le grand rhomboèdre, où l'on a 24 solides pour une surface de 48 triangles. Tous ces rapports sont en effet égaux à 1/2.

 

On saisit par là que le gnomon est un certain rapport d'identité, particulièrement profond, entre nombres et figures. Même si certains, avec quelque raison peut-être, préfèreront n'y voir qu'une vaste tautologie.

 

Cette relation généralisée permet de conjecturer que, pour le rhomboèdre d'or d'angle 72°/108° et son solide de Dürer associé, le rapport 2/3 qui est celui des angles du losange, devra se retrouver dans la composition interne du rhomboèdre, aussi bien que dans la division de ses faces ; et que, selon toute vraisemblance, la solution de ce problème devra revêtir la forme d'un pavage de Penrose en trois dimensions.

 

 

 

 

 

Chapitre 2

NOMBRES GNOMONIQUES ET NOMBRES MIROIRS

 

 

 

On peut remarquer que les nombres 8 et 14, qui apparaissent dans la composition du solide de Dürer, ne sont pas des inconnus, puisqu'on les retrouve dans la nomenclature des polyèdres gnomoniques de rang 2.  Nomenclature où l'on retrouve aussi, par induction, les nombres 27 et 54, intervenant quant à eux dans le lambda de Platon, qui correspondent si l'on peut dire au "centre caché" de cette structure d'objets. En demandant grâces pour la trivialité de ces calculs, qui n'ont d'autre fin que de mettre en lumière cet aspect structurel des rapports arithmétiques.

 

POLYEDRES GNOMONIQUES DE RANG 2

 

Tétraèdre            Cube             Octaèdre                                  Icosaèdre               Total

5                           8                    14                                           81                       108

5               +          8          +        14    =     27

                                                                  27     =    54/2    =    81/3        =          108/4

 

La seconde équation pouvant être vue comme une tétractys, dont les 10 unités-points seraient des cubes gnomoniques de rang 3, de valeur 27.

 

 

On peut encore noter que les propriétés des multiples de 9 - très appréciées de Dante - permettent de développer, à partir du nombre 108, une série continue de rapports proportionnels alternés entre nombres miroirs. Ainsi 18 est à l'égard de 108 dans le rapport 1/6, tandis que son "miroir" 81 est à l'égard de 108 dans le rapport 3/4. 27 est à l'égard de 108 dans le rapport 1/4, tandis que son miroir 72 est à l'égard de 108 dans le rapport 2/3. 36 est à l'égard de 108 dans le rapport 1/3, tandis que son miroir 63 est à l'égard de 108 dans le rapport 7/12. Enfin 45 est à l'égard de 108 dans le rapport 5/12, tandis que son miroir 54 est à l'égard de 108 dans le rapport 1/2. Accolés à leur complément, les nombres miroirs forment des nombres palindromes, eux mêmes dotés de propriétés spéciales. Aux extrémités de ce cycle se trouvent le nombre 9 (108 x 1/12), diviseur de tous les autres, qui, lorsqu'on l'exprime sous la forme 09, est le miroir de 90 (108 x 5/6), et enfin le nombre 99 (108 x 11/12), sous l'égide duquel Virgile et Dante ont tous deux placé leur oeuvre majeure, comme l'a montré André Charpentier. Ce nombre "terminal" est exclu du mouvement tournant qui entraîne tous les précédents, en ce qu'il est miroir de lui-même, et donc déjà palindrome. Sous ce regard, il peut donc apparaître comme le point de "fixation" autour duquel gravitent tous les autres, ce qui explique que ces poètes pythagoriciens aient vu en lui l'image du "moteur immobile" de la manifestation universelle.

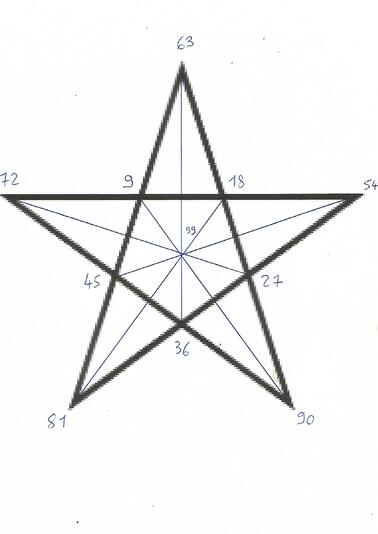
Ceci se comprend encore mieux si l'on dispose tous ces nombres autour d'un pentagramme, de la manière indiquée ci-dessous, puisqu'on s'aperçoit alors que tous les segments reliant entre eux deux nombres miroirs convergent naturellement au centre 99, qui correspond à chaque fois à leur somme.

 

Si l'on adopte pour le pentagone intérieur une disposition "horaire", alors le pentagone extérieur se disposera lui-même de façon "anti-horaire". Les nombres correspondent donc ici exactement aux propriétés de la figure, symbole traditionnel de l'analogie inversée du microcosme et du macrocosme, mais aussi de l'alternance universelle des rythmes cosmiques.

Si l'on relie tous ces points par un tracé continu suivant l'ordre croissant des nombres qui leur correspondent, et si l'on joint le dernier (99) au premier (9), on obtient une figure appelée noeud vital, qui s'apparente à plusieurs symboles connus, tels que le symbole de l'infini, le noeud trèfle ou l'éperluette, tout en se distinguant nettement de chacun d'eux.

 

 

Compte tenu de la logique interne du pentagramme, où les milieux des différents segments convergeant vers le centre 99 sont supposés équivaloir à la somme des nombres associés à leurs extrémités - et ceci indéfiniment, - l'action de joindre, par un dernier segment, le nombre 99 au nombre 9, peut être comprise comme équivalant à intégrer dans le pentagramme le nombre 108, en tant que milieu virtuel de ce dernier segment.

Et pour clore ce chapitre de transition, on pourra relever que le rapport de 99 à 108 est identique à celui du solide de Dürer à son rhomboèdre associé (11/12).

 

 

 

 

 

 

 Chapitre 3

 ISOMORPHISME DU PENTAGRAMME ET DU SOLIDE DE DÜRER

 

 

 

Le rapport entre le pentagramme "modulo 9" et le solide de Dürer n'est pas seulement proportionnel, mais d'octave (11 points pour le pentagramme avec son centre / 22 petits solides pour le solide de Dürer) ; et, dans ce dernier chapitre, nous allons voir qu'il existe une application qui projette les 11 points du pentagramme sur les onze segments reliant deux à deux les centres des 22 petits solides du solide de Dürer, (plus exactement, l'application se fait sur les milieux de ces segments), et réciproquement, - application dans laquelle sont conservées toutes les relations de symétrie, mais aussi de polarité du pentagramme, et grâce à laquelle le solide de Dürer s'intègre naturellement dans ce pentagramme.

 

Dans la représentation ci dessous, les boules blanches correspondent donc aux centres des 22 petits solides du solide de Dürer, solides dont la nature, tétraèdre ou octaèdre, est précisée sur la boule. Ces 22 boules blanches sont assemblées par paires et forment 11 segments. Les onze petites boules noires qui sont les centres de ces segments, correspondent aux 11 points du pentagramme (avec son centre 99).

 

La structure se divise en trois parties : inférieure, supérieure et médiane. Dans la partie inférieure, les segments 18, 27 et 36, forment les arêtes verticales d'un prisme à base triangulaire, avec le segment 9 pour axe polaire principal.

Les segments 63, 72 et 81 forment un prisme identique au premier, avec le segment 90 pour axe polaire; ces deux prismes sont disposés l'un au dessus de l'autre en « sceau de Salomon ». 

Ces huit segments verticaux, occupant les parties inférieure et supérieure du solide, ont tous la même composition : un octaèdre et un tétraèdre; tandis que les trois segments occupant la partie médiane sont composés, eux, de 2 tétraèdres chacun.

 

La structure médiane forme également un sceau de Salomon, composé, non de 2 prismes, mais de 2 simples triangles. Ici on a favorisé une présentation permettant de distinguer plus aisément les 3 segments, mais pour que la figure soit géométriquement exacte, il conviendrait que les 2 triangles indiqués en pointillé, inférieur et supérieur, soient positionnés exactement l'un au dessus de l'autre. Les segments 45 et 54 sont tous deux horizontaux, mais situés à des hauteurs différentes, le 45 plus bas, le 54 plus haut. Quant au segment 99, il possède un point sur le même plan horizontal que le segment 45, et l'autre sur le même plan horizontal que le segment 54. Les segments 45 et 54 sont bien parallèles, comme l'indique la figure ; en revanche, le segment 99 est perpendiculaire au plan formé par ces segments. En joignant par deux segments complémentaires les segments 45 et 54, on obtient un parallélogramme (un losange "vesica piscis" d'angle 60/120°) ; le segment 99 traverse ce losange en plein centre, perpendiculairement.

Ces trois segments forment véritablement le coeur de la structure. Le plan formé par les segments 45 et 54 est incliné de 45° par rapport au plan horizontal, et se situe donc à mi distance angulaire entre le plan horizontal et l'axe vertical; tandis que le segment 99, orthogonal à ce plan 45, 54, est - relativement au même axe vertical - incliné de 45° en sens contraire.

 

 

Symétries et polarités 

 

Ce qui est intérieur dans le pentagramme (les points 9, 18, 27 et 36) correspond à ce qui est inférieur dans le solide de Dürer (les segments 9, 18, 27 et 36).

 

Ce qui est extérieur dans le pentagramme (les points 63 à 90), correspond à ce qui est supérieur dans le solide (les segments 63 à 90).

 

Ce qui est intermédiaire dans la séquence du pentagramme (les points 45, 99 et 54), correspond à ce qui est médian dans le solide, (les segments 45, 99 et 54).

Enfin, ce qui est au centre dans le pentagramme, le point 99, correspond à ce qui est au centre dans le solide de Dürer; puisqu'en effet le centre du segment 99 correspond au fameux "point vert" évoqué ailleurs sur ce site, qui est le barycentre du solide de Dürer.

Toutes les relations de polarité entre 2 points opposés du pentagramme par rapport au centre 99, se retrouvent dans le solide de Dürer. Ainsi, dans le solide de Dürer, le segment 18 est, polairement, antagoniste du segment 81, le segment 27 du segment 72, le segment 36 du segment 63, le segment 45 du segment 54, et le segment 9 du segment 90. Tandis que le segment 99, comme il se doit, est antagoniste de lui-même. Et il y a mieux encore : si l'on joint par leurs centres toutes ces paires de segments antagonistes du solide de Dürer, on constate que toutes les droites joignant ces segments par leurs milieux passent par le centre du segment 99.

 

Ce qui est polaire dans le solide de Dürer, (en considérant comme axe polaire principal, l'axe vertical haut / bas qui est l'axe d'étirement du solide), à savoir les segments 9 et 90, correspond, dans le pentagramme, au « début » et à la « fin » de la séquence; - car dans le pentagramme aussi la séquence naturelle commence à 9 et finit à 90, puisque le point 99 a été installé à son juste « moment », entre les points 45 et 54.

 

Enfin, l'orientation alternée du sens de la construction ; d'abord « horaire » de 9 à 45, puis anti-horaire de 54 à 90, est également respectée. Le segment 99 correspond au plan de symétrie de part et d'autre duquel se divisent, en s'inversant, ces deux mouvements, le premier « dextrogyre », le second « lévogyre ». Les deux structures ont pour squelette commun une double spirale, bidimensionnelle pour le pentagramme, tridimensionnelle pour le solide de Dürer, où elle se développe en double hélice - spirales dont la première est centripète et dextrogyre, et dont la seconde est centrifuge et lévogyre.

La structure sous-jacente aux deux figures peut être schématisée par l'illustration ci dessous :

 

 

 

 

 

Du pentagramme au nid d'abeilles

 

Le solide de Dürer peut donc n'apparaître que comme un développement en trois dimensions de la structure bidimensionnelle qui est celle du pentagramme. Cependant, alors que le pentagramme est une structure de symétrie pentagonale, associée au nombre d'or et aux pavages de Penrose, le solide de Dürer – placé tout entier sous le signe du sceau de Salomon – relève, quant à lui, de la symétrie du "nid d'abeille" tétra-octaédrique, propre à sa constitution gnomonique, symétrie résultant d'un pavage continu de l'espace par des tétraèdres et des octaèdres, comparable à celui que l'on peut obtenir avec des cubes. L'intégration du solide de Dürer dans le pentagramme fait donc apparaître une supersymétrie – ou encore une super dualité – entre ces deux types de symétrie.

 

                                          

                                         pentagramme                   nid d'abeille tétra-octaédrique

 

 

Or, on remarque que dans notre solide de Dürer, la symétrie pentagonale est celle qui régit les « milieux » des objets appartenant à la seconde, à la symétrie du nid d'abeille. La première se présente ainsi comme étant « au coeur » de la seconde, comme son principe de mouvement, ou de développement ; ou encore, la première semble correspondre à l'aspect « intérieur » d'une réalité, dont la seconde représenterait l'aspect « extérieur ».

 

 

 

Remarque ponctuelle

 

On a fait le choix, pour cette étude, de référencer les solides par les points qui sont leurs centres, afin de mettre en évidence ensuite les "milieux" des segments joignant ces centres, mais il convient de préciser que, dans la logique du gnomon, les petits solides, qui ont le statut d'atomes et la valeur discrète de monades, peuvent parfaitement être considérés eux-mêmes comme des points, de sorte que nos boules blanches auraient tout aussi bien pu désigner ces solides eux-mêmes. On aurait alors eu 11 segments composés uniquement de 2 points; à la réserve que, dans ce cas de figure, les lignes joignant ces boules auraient été superflues, puisque, pour tous ces segments, les deux solides sont tangents, soit par une face (pour les segments tétraèdre-octaèdre), soit par un sommet (pour les segments tétraèdre-tétraèdre). Les centres des segments auraient donc coïncidé avec des lieux intersticiels purement virtuel et de valeur nulle, autrement dit avec des points "euclidiens", lesquels, dans leur compréhension juste, ne peuvent représenter que des lieux vides d'objet. De ce point de vue, la symétrie pentagonale peut donc apparaître, tout aussi légitimement, comme la symétrie régissant les vides intersticiels de la structure du nid d'abeille.

 

 

Le symbolisme du pentagramme

 

En laissant de côté toute considération liturgique, il est possible, en conclusion, de toucher ici un mot du symbolisme du pentagramme.

 

Dans sa représentation classique sous forme de noeud à 5 sommets, le pentagramme est un noeud mortel, qui se rapporte au démembrement de "l'homme primordial" et dont les points de référence (situés au centre des 5 petits triangles - branches de l'étoile) sont en réalité des "points de casse", qui correspondent dans le corps humain à : nuque, épaules, et hanches. Ce noeud agit donc de façon "constrictrice", comme mû d'une énergie "auto-serrante".

 

En passant par le point central, on a, comme pendant de ce noeud mortel, le noeud vital... dont la chose la plus importante à remarquer, sans doute, est qu'il n'est pas un noeud. En effet, si on le saisit par un coin, il se délace et se résout en une simple corde circulaire, de sorte que son aspect "nodal" s'avère finalement n'être qu'une illusion.

 

 Le 18.04.2017