IV. SYMETRIE MODERNE / SYMETRIE PYTHAGORICIENNE

 

 

La différence entre mathématique moderne et mathématique pythagoricienne pourrait, en guise d'approche, être caractérisée par la façon dont chacune appréhende en quelque sorte naïvement, spontanément, de par le style mathématique qui lui est propre, le problème de l'espace et de sa représentation. La mathématique moderne semble considérer comme réel, et même comme unique réel, le "substrat" ou le fond indéfini de l'espace intelligible, quelque soit le nombre de dimensions qu'elle veuille lui prêter, indépendamment des objets que l'on peut définir à l'intérieur de lui. Cet espace a pour elle l'apparence d'un donné objectif, déjà développé, au sein duquel règnent, en tout point, l'"isotropie" ou l'équivalence ontologique, et  la symétrie, au sens moderne et saturé d'indifférenciation. Enfin, cet espace est conçu comme indépendant de la situation native, ou naturelle, de l'homme. L'espace pythagoricien est, au contraire, un espace originellement dual, où la définition du fond indéfini est inséparable de celle d'objets définis, et où règnent, de ce fait, la différence, la singularité et la polarisation en tout point. La géométrie pythagoricienne, y compris la plus fondamentale, intègre de plein droit les notions naturelles de l'orientation et de la chiralité.⁽¹⁾ Mais plus important encore, l'espace pythagoricien est un espace qui a une histoire, un développement; c'est un espace dont la structure profonde est chronogénétique, faite de temps et de nombre, et où règne de ce fait aussi la différence en tout point du temps. - Ces remarques, toutefois, appellent quelques éclaircissements complémentaires.

La définition moderne de la symétrie, synonyme d'uniformité ou d'indifférenciation absolue (la symétrie moderne est en effet "ce qui ne change pas" pour tels mouvements de l'objet), est une extension mathématique correcte, légitime, de la définition "traditionnelle", ou pythagoricienne, synonyme de commensurabilité, ou de commune mesure. Entre les deux, il n'y a pas de réelle rupture. La moderne n'est qu'une maximisation de l'ancienne, obtenue par amplification progressive de son concept; - mouvement de généralisation qui est en lui-même naturel en mathématique, et dont le moment décisif aura été, ici, la théorie des groupes de Galois. Cependant, dans la nouvelle définition, le référent ultime du concept de symétrie n'est plus la symétrie d'objets, mais celle de l'espace. La saturation du concept joue donc bien ici le rôle de liquidateur de contenu ou de déterminité ontologique, au bénéfice de la seule puissance du signe, qui est caractéristique des généralisations de la mathématique moderne. Le tort de la mathématique moderne n'étant pas, fondamentalement, de pratiquer ces généralisations, mais plutôt, en vertu d'une politique de la "table rase" intellectuelle, de considérer systématiquement comme plus essentiel cet aspect final de la vie du concept, qui est celui de son détachement et de sa transformation en signe-outil, au mépris du chemin entier de la pensée qui a produit ce signe et l'a conduit, par des mouvements comptés, jusqu'à cet état, ou cette phase particulière de son développement. Il en résulte un certain appauvrissement, car, à force de privilégier l'espace au détriment de l'objet, la réflexion épistémologique sur la symétrie finit par prendre les allures d'une spéculation sur les propriétés hypothétiques d'un "contenant absolu", d'un espace en soi et pour soi, - tenu de ce fait pour l'espace "réel", - qui nous semble être une idée sans pertinence mathématique, dans la mesure où la notion même de "contenant" implique, selon nous, qu'il ne peut s'agir que d'une certaine forme, d'une formulation parmi d'autres possibles, (fût-elle la forme spécifique de notre univers, celle de notre pensée, ou l'une et l'autre à la fois), - sans aucun des caractères "d'absoluité" que cette conception moderne voudrait qu'elle puisse posséder. L'idée même que puissent exister des propriétés absolues de l'espace, - sensible ou intelligible, - occulte la possibilité permanente, pour la pensée, de concevoir un espace qui n'ait encore jamais été imaginé.

 

Il revient à Jean-Luc Périllié d'avoir pleinement réhabilité, sur le plan philosophique, la notion pythagoricienne de symétrie, dans sa signification littérale et originelle de commensurabilité, de commune mesure, ou plus simplement encore, de proportion; mais aussi, d'avoir montré sa position centrale dans la mathématique pythagoricienne, qui en fait un véritable trait d'union entre les différents concepts mathématiques évoqués sur ce blog.

La symétrie apparaît, dans la genèse du nombre, lorsque celui-ci se fait mesure, "logos"; lorsqu'il s'affranchit du mutisme de sa condition monadique originelle, pour se déployer en tant que rapport.

Dans sa définition la plus rigoureuse, la symétrie pythagoricienne est la commune proportion des différentes parties d'un tout, entre elles aussi bien qu'à l'égard de ce tout.

Cette définition peut, naturellement, être illustrée par des opérations géométriques très simples, dont les plus originaires sont, sans le moindre doute :

1- Le partage d'un segment en deux parties égales.

2- Le partage d'un segment en "extrême et moyenne raison", (c'est à dire : tel que la plus petite partie soit à l'égard de la plus grande, comme la plus grande est à l'égard du tout), opération dont on sait qu'elle permet de définir géométriquement le nombre d'or.

Si l'on considère la position des 3 points de référence du segment, (Origine, Moyen et Extrême), chacune de ces opérations correspond à une médiété particulière : la médiété "arithmétique" dans le premier cas, médiété dont le pprm (plus petit rapport mineur) est celui qui présente l'envergure maximale, puisqu'il est égal à 1; et la médiété Nicomaque 10 ("de Fibonacci") dans le second , dont le pprm est celui qui présente l'envergure minimale, puisqu'il est égal à zéro.⁽²⁾

Du point de vue qui est géométriquement le plus originaire, la mathématique pythagoricienne tient tout entière dans cet intervalle, dans le paradigme mathématique défini par ces deux cas particuliers de symétrie, que l'on peut légitimement qualifier de saturés, puisqu'ils correspondent aux limites naturelles indépassables de ce concept.

Quant à la source arithmétique la plus profonde de cette notion, elle est à rechercher, selon toute apparence, dans la symétrie qui est en quelque manière la plus intérieure à la mathématique : celle qui se déploie dans la relation que les opérations arithmétiques entretiennent entre elles. Symétrie qui se présente, de prime abord, comme une interrelation généralisée, de nature organique, entre toutes les opérations primitives de l'arithmétique, de laquelle procède finalement, comme une expression renversée du même processus, le nombre naturel lui-même.

 

 

La symétrie inter-arithmétique

 

Dans la conception pythagoricienne, - du moins ce qu'on peut en déduire du cadre mathématique a priori qu'est la théorie du gnomon - les relations de symétrie primordiales semblent se réduire à un appareil de structure biternaire, correspondant au ternaire des "lois de composition" de l'arithmétique :
 
1. addition - soustraction                        (nombres monadiques)
2. multiplication - division                                        (logoï)
3. puissance - racine                                             (puissances)
 
Appareil dans lequel une symétrie de translation "haut-bas" se superpose aux symétries de rotation axiale "gauche-droite", qui sont les relations entre opérations inverses : toutes symétries que l'on trouve illustrées dans les structures les plus simples de la théorie du gnomon, telles que les polygones et polyèdres gnomoniques, ou les spirales logarithmiques.  

Les relations inter-arithmétiques, telles qu'elles sont déployées dans la structure du gnomon, sont comparables à des transformations géométriques entre objets duaux, dont l'exemple type est, en mathématique pythagoricienne, la dualité des solides réguliers. Ainsi, le carré gnomonique de rang 4 se transforme en spirale de Théodore, (et par suite, l'opération "puissance" en l'opération "racine"), par un retroussement, un redéploiement du même genre que celui par lequel un solide régulier se transforme en son dual. Dans la logique pythagoricienne, ces deux transformations ont une matrice commune qui est précisément le gnomon : le gnomon du carré pour la dualité "puissance-racine", le gnomon du triangle pour la dualité des solides réguliers. La théorie du gnomon peut donc apparaître, de ce point de vue, comme un ensemble de "solutions vides" permettant de transformer des nombres entiers en objets géométriques simples, et inversement. Le gnomon est le cadre d'une correspondance, d'une coordination entre deux ordres de réalité mathématiques : d'une part, le nombre entier monadique, avec le réseau a priori, le "filet" des opérations arithmétiques primitives (addition, multiplication, puissance), qui résultent de sa seule production, de son "empilement" concret dans l'espace-temps; d'autre part, les objets les plus simples de la géométrie (objets premiers, polygones et polyèdres réguliers) et les relations de symétrie profondes, aussi bien internes qu'externes, que ces objets entretiennent entre eux; - ces deux processus étant, finalement, regardés comme deux aspects d'une seule et même réalité transcendante, le nombre, qui est fondamentalement un être ensemble, un consteller : réalité dans laquelle les catégories de l'opération et de l'objet ⁽³⁾ - et même, ultimement, celles du nombre et de la figure - demeurent encore confondues, conjointes.

 

 

*

 

Le premier rang de la structure ternaire ci-dessus est celui des processus les plus généraux mis en oeuvre par la mathématique pythagoricienne, les uns additifs, comme la tétractys ou la théorie des objets premiers, les autres soustractifs, comme les médiétés. Le second rang est celui des logoï, ou rapports d'entiers - terme qui, dans sa compréhension profonde, désigne aussi bien les fractions que, par induction, les produits d'entiers. Le rapport rationnel, symbolisé aujourd'hui par la fraction (x/y), est à la base le cadre dans lequel la notion de sym-métrie reçoit son complet développement, aussi bien technique que conceptuel. La qualification de logoï pour les objets de ce rang est des plus importantes, et se réfère à la question du nom mathématique qui, comme on peut tenter de l'exposer ici en quelques traits, est épistémologiquement profonde en science pythagoricienne. Les logoï sont des rapports fonctionnels entre nombres; autrement dit quelque chose qui n'est déjà plus nombre, mais mesure, "raison", non plus seulement perception et sensibilité, mais compréhension et intelligence, et qui se produit entre les nombres. Ils correspondent à un moment où le nombre, pour exhiber ce qu'est son opération profonde, doit se tourner vers autre chose que lui-même, révéler une partie plus importante de ce sur quoi, comme de ce grâce à quoi s'exerce cette opération; - et par suite recevoir, du fait de cette exposition à lui-même, de nouveaux noms mathématiques. Ce second moment du nombre peut donc être caractérisé comme celui où apparaissent, dans son sein, de nouvelles fonctions productrices de noms et de langage,⁽⁴⁾ contrairement aux processus monadologiques du niveau inférieur, qu'ils soient additifs ou soustractifs, dont la nature propre implique, au contraire, de pouvoir être montrés de façon mathématiquement suffisante, sans mots ni langage, mais avec d'autres vêtements matériels en quelque manière équivalents, tels que des boules, des jetons, ou tout autre objet pouvant faire office de monade; même s'il est évident que ces objets pourront, rétrospectivement, être envisagés de l'une ou l'autre manière, sensible ou intelligible. Enfin, le troisième rang est celui des puissances, terme qui, anciennement, était générique et pouvait désigner aussi bien les exposants que les racines,  (précisément réunis par ce terme dans une catégorie synthétique) domaine illustré notamment, sur le plan le plus fondamental, par la relation de dualité qui existe entre la spirale de Théodore et le carré gnomonique.⁽⁵⁾ Ce troisième moment peut être regardé comme la réunion, ou l'addition des deux premiers; puisque la puissance est une opération qui retient, comme propriété du premier niveau, l'identité monadologique, le rapport à l'objet "soi-même", et comme propriété du second, la fonction : "produit", qui est à comprendre ici dans son sens littéral de "production". En tant que coordination des moments 1 et 2, ce moment peut donc, de fait, apparaître comme celui où les objets des premiers rangs, monades et logoï, développent leur pleine potentialité, leur pleine puissance. C'est là, en particulier, que la notion géométrique de dualité reçoit son ultime développement, et se présente comme une interface complète, "auto-suffisante", non seulement entre nombres et  figures, (entre rapports arithmétiques et rapports géométriques au sein d'un même objet), comme c'était le cas dans la théorie des objets premiers, dont l'aboutissement est la construction du tétraèdre, mais, plus universellement, entre objets et opérations mathématiques, considérés comme potentialités pures, continuellement convertibles et réversibles les unes en les autres, comme c'est le cas dans la théorie du gnomon, et plus précisément, au coeur de cette dernière, dans l'équation de la dualité des solides réguliers, dont le tétraèdre est cette fois l'objet le plus simple, la pièce de construction la plus élémentaire. Le tétraèdre, - structurellement : le triangle gnomonique de rang 2, - apparaît donc ici comme le vecteur de la transition et de la continuité logique entre un ordre et l'autre, entre l'ordre monadologique "interne", constitutionnel, qui est celui des objets premiers, et l'ordre "externe" qui est celui de la croissance "puissancielle", (originellement carrée ou gnomonique), et celui de la dualité exhaustivement développée des solides réguliers. Le moment médian, ou "intermédiaire", le logos, (représenté ici par le gnomon et sa fraction de 1/3), apparaissant dès lors comme la simple paroi, (l'"interface"), comme la forme et la solution vide de cette transition, de cette bascule entre un ordre et l'autre; et l'on saisit par ce chemin que ce fameux logos correspond bien alors au concept de la logique dans sa compréhension la plus vraie, qui définit cette science comme la forme vide de la mathématique. ⁽⁶⁾

C'est précisément par la vertu de cette viduité, par la frustration intellectuelle qu'elle suscite, si l'on peut dire, que la logique est génératrice, non de contenu mathématique - ce dont elle est parfaitement incapable, - mais de contenus linguistiques.

Concernant le troisième étage, on peut encore remarquer que les "puissances" (racines ou exposants) carrés et cubiques se distinguent, par une certaine primauté ontologique, (mais aussi, par une certaine analogie avec la structure biternaire qui est celle du système général), des ensembles indéfinis d'objets auxquels ces mêmes éléments participent d'autre part, dans le cadre d'une quelconque relation de famille avec leurs successeurs. Racines et exposants carrés et cubiques forment, de ce fait, une catégorie arithmétique indépendante, et close en tant que telle : en raison là encore de ses implications gnomoniques, illustrées au niveau le plus simple - et mathématiquement originaire - par l'exemple des gnomons du carré et du cube, dont ces puissances tirent leurs noms mêmes.

 

⁽¹⁾ Même si, de façon plus juste, la tétractys n'intègre pas par un acte particulièrement "décisoire" les catégories du haut, du bas, de la droite et de la gauche, mais se contente plutôt de les accueillir par une attitude "non-agissante".

⁽²⁾ Sur ce sujet, voir, en page 2 de ce blog, les gloses 1 et 2 de l'article : Rectangle de Fibonacci.

⁽³⁾ Le nombre est par excellence, en pythagorisme, une réalité dans laquelle les catégories de l'opération et de l'objet sont comprises synthétiquement, ce que l'on pourrait exprimer de plusieurs manières, comme : "Le nombre est une opération qui se prend elle-même pour objet" ou "Le nombre est un objet produit par son opération-même".

⁽⁴⁾ La mathématique pythagoricienne admet donc la nécessité, pour toute mathématique, de sortir du nombre et de sa "pureté", pour s'établir dans la loi du Nom, à un moment de son développement qui, même si il n'est pas premier, est plus précoce que ne le voudrait, en général, la mathématique moderne, avec ses prétentions un peu vaines et superficielles, finalement appauvrissantes, qu'elles puissent être "formalisantes" ou "axiomatisantes", à vouloir survivre indéfiniment en dehors de tout langage naturel, au nom d'on ne sait quel défi adolescent que la science se serait, sans but particulier, lancé à elle-même.

⁽⁵⁾ Sur la correspondance un peu plus générale entre spirales et gnomons géométriques pythagoriciens, voir, en page 2 de ce blog, les articles : Spirale de Théodore, Rectangle de Fibonacci, et la glose : Pentagone de Padovan. 

⁽⁶⁾ Dans le développement de la physique moderne, les logoï ou rapports d'entiers pythagoriciens ont trouvé la confirmation éclatante de leur pertinence théorique, en tant que principes de mouvement d'abord, (fonction qui était déjà la leur dans les spéculations cosmologiques et "musicales" dont le Timée offre l'exemple, comme certains l'ont récemment redécouvert), puis plus généralement, en tant que principes de charge énergétique. Ces applications se sont développées, notamment, dans deux domaines essentiels : la cosmologie, où les mouvements des astres se laissent souvent réduire à des rapports d'entiers, - ainsi les mouvements de Mercure (3/2) ou de la Lune (1/1), identiques, respectivement, aux rapports de la quinte et de l'unisson; - et la physique quantique, où ces mêmes rapports d'entiers ont une valeur paradigmatique, dans la quantification des spins, aussi bien que des charges électriques affectant les différentes particules. Malgré ces divers succès en science physique, la notion pythagoricienne de logos attend toujours d'être réhabilitée dans le domaine philosophique, où personne ne s'est encore risqué à entreprendre, en sa faveur, une tentative de justification systématique.

 

 

  

  

III. DUALITE MATHEMATIQUE ET SYNTHESE A PRIORI

 

  

La notion de dualité constitue pour Granger une catégorie philosophique, dont l'acception est dérivée des définitions mathématiques de ce terme, elles-mêmes variées, sans se confondre avec l'une d'entre elles en particulier. Citons l'une des définitions données par Granger de cette notion, - définitions qui, pour être non seulement diverses, mais souvent, comme ici, prudentes et programmatiques, ne doivent pas masquer le caractère urgent et impérieux qu'elles revêtent, sans nul doute, pour leur auteur.

"Au sens où nous l'entendons, la notion de dualité comme catégorie philosophique conduirait à formuler le principe de la nécessité d'une détermination réciproque de tout système d'objets de pensée et d'un système d'opérations intellectuelles associé."

A cette définition liminaire, il faut ajouter cette précision tout aussi essentielle, que, dans le développement de la mathématique, ce qui était objet d'un certain point de vue antérieur, peut, à son tour, devenir opérateur d'un point de vue nouvellement formulé, - la dualité devenant ainsi le vecteur, non seulement de la continuité du raisonnement ou du discours mathématique, mais de la constance d'une certaine forme logique.

La dualité grangérienne a vocation à se substituer à la notion kantienne de "synthétique a priori", dont elle reprend toutefois les réquisitions. Un système opérations-objets dual et consistant peut être considéré comme un "ensemble" synthétique a priori de vérités mathématiques.  Mais la notion  de dualité est aussi intimement liée à celle de nature mathématique, et à la définition de ce que peut être un objet mathématique naturel, dans la mesure où elle tend à associer la définition des objets mathématiques, autant à des lois physico-chimiques de la nature, qu'à des actions concrètes de l'homme, qu'elles soient d'ordre psychique ou physique, - sans exclusion du musculaire, - d'un caractère assez universel, idée qu'avait déjà thématisée, en son temps, la théorie de la forme, ou même la pensée formelle en général. 

Concernant cette catégorie, ce que l'on peut remarquer d'abord est son caractère "moniste", d'une part, parce qu'elle ne s'inscrit pas dans un ensemble de catégories de même niveau, mais se présente comme un véritable "singleton" catégoriel, d'autre part, parce que la dualité elle-même est réellement une, même si elle contient le deux, en ce qu'elle s'exprime, comme on l'a dit, par le maintien ou la constance, d'application en application, d'une certaine forme logique; en quoi elle se veut précisément synthèse; et par où se justifie aussi sa prétention singulière à être apparemment, pour Granger, la catégorie ultime de la science

Dans un cadre différent, qui est celui - métaphysique - de la définition du symbolisme et de la pensée symbolique, René Guénon a, lui aussi, donné de brillantes définitions de la synthèse et du synthétique, qui ont plusieurs traits congruents avec celle esquissée ici. 

  

 

Dualité des solides réguliers 

 

Polyèdres inscrits : tétraèdre                     octaèdre                         icosaèdre 

                          

Polyèdres circonscrits : tétraèdre                  cube                            dodécaèdre

 

Le tétraèdre, à gauche, est le dual de lui-même. Dans cette relation généralisée, l'ensemble des relations de dualité entre solides réguliers considérés par paires, est déductible, ou dérivable, du développement gnomonique tridimensionnel d'une seule et unique structure géométrique : le triangle équilatéral. En effet, les trois polyèdres primitifs - ici en couleurs et inscrits, dont ceux en arêtes rouges et circonscrits (dans la succession desquels on retrouve les valeurs 3 - 4 - 5 du triangle isiaque) sont les duaux; - ces trois polyèdres inscrits peuvent être construits au moyen de triangles gnomoniques de rang 2 : 1 pour le tétraèdre, 2 pour l'octaèdre, 5 pour l'icosaèdre. Autrement dit : les polyèdres réguliers sont contenus de manière synthétique a priori dans les seules propriétés intrinsèques de développement gnomonique, d'une part, et de clôture géométrique tridimensionnelle, d'autre part, qui sont celles du triangle équilatéral. Ou encore, le triangle gnomonique de rang 2 est la constante logique du système opérations-objets dans lequel consiste et se déploie ici la nature, la définition même des polyèdres réguliers.

tétraèdre + octaèdre + icosaèdre = (1 + 2 + 5) x triangle gnomonique de rang 2

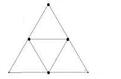
Quant à la série des polyèdres rouges : tétraèdre, cube, dodécaèdre, elle s'obtient par la transformation des premiers polyèdres, d'objets qu'ils étaient, en opérateurs, les sommets de ces polyèdres devenant les centres de référence des faces des polyèdres circonscrits, mathématiquement suffisants à les définir. A leur tour, ces polyèdres rouges peuvent devenir les opérateurs de la construction des trois premiers, par une transformation duale de la précédente.

 

La synthèse duale revient, comme on le voit, à demander qu'une multitude d'objets et d'opérations mathématiques soient reconduits, ensemble, à l'unité d'un seul principe, d'une seule pensée. En généralisant cet exemple à l'ensemble de la science, on peut le traduire par la réquisition suivante : "S'il y a unité de la science, alors cette unité doit consister en une pensée", - réquisition qui constitue une bonne définition de ce que représente, pour la pensée pythagoricienne, la tétractys.

 

 

 

Dualité et symétrie, deux aspects de la biunité du nombre

 

Dans sa compréhension profonde, la notion de dualité s'enracine dans la notion pythagoricienne de symétrie, en son sens littéral et originel de commensurabilité, de commune mesure. Une relation de dualité est une relation qui mesure ensemble deux aspects d'une même réalité, qui les tient et les produit ensemble dans un même geste, à partir d'une position "neutre", non polarisée, depuis laquelle ils se transforment l'un en l'autre, - à partir d'un statut originel unique qui n'est, véritablement, ni celui d'opérateur, ni celui d'objet, mais la pure potentialité d'être indifféremment l'un ou l'autre.⁽¹⁾

Une relation de dualité n'est qu'une relation de symétrie forte, développée jusqu'au point où elle est auto-suffisante, (la langue moderne dit avec justesse consistante), c'est à dire productrice, par sa seule potentialité, d'objets et d'opérateurs mathématiques originaux ou "naturels", d'ailleurs indéfinis en quantité.

"Symétrie" et "dualité" ne sont donc que différents noms mathématiques, correspondant à différents degrés de développement, d'une seule et même réalité profonde, qu'on pourrait appeler la biunité du nombre naturel; cet "état" primordial et synthétique du nombre, en lui-même insaisissable, que la logique représente alternativement par les connecteurs "ni... ni...", et "et", dans lequel il n'est, ni objet ni opération, mais l'un et l'autre à la fois, ni cardinal ni ordinal, mais l'un et l'autre à la fois, ni monade ni dyade, mais l'un et l'autre à la fois, voire en pythagorisme conséquent, ni nombre ni figure, mais l'un et l'autre à la fois; biunité dont le principe nous est présenté, par la notion de symétrie, sous son aspect purement arithmétique, et par celle de dualité, sous un aspect géométrique, topologique, et plus généralement structurel, mathématiquement plus développé.

 

⁽¹⁾ Bien que le sujet ne puisse être abordé ici, on peut remarquer que, du point de vue général de la science, la notion de dualité est presque aussi importante en physique qu'en mathématique; et la description qui en est faite ici pourrait faire penser à l’une des dualités les plus célèbres de la physique, la dualité onde-corpuscule, au fondement de la mécanique quantique, avec d’autant moins de surprise que la théorie ondulatoire est elle-même directement issue de spéculations pythagoriciennes, notamment archytéennes. Dans la recherche plus récente, on peut aussi penser à la théorie des cordes, avec la notion importante de "dualité de cordes".

 

 

 

 

 

    

 

II. LA CONSTRUCTION PYTHAGORICIENNE DE LA GEOMETRIE.

 

 

En dehors de la théorie du gnomon, l'un des aspects les plus importants de la mathématique pythagoricienne réside dans la façon de définir les dimensions et les objets premiers de la géométrie, par une méthode qui est foncièrement différente de celle d'Euclide, en ce qu'elle consiste à associer de façon rigoureuse, à chacune des dimensions ou des objets qu'elle définit, la quantification des opérations de pensée correspondantes à ces objets, comme à ces dimensions. Le référent absolu n'est autre que le temps, mais pas n'importe quel temps, le temps des opérations mathématiques; ici, l'opération : "poser un point dans une nouvelle dimension".

  

1                  2                     3                        4

 

4 objets, 4 dimensions. Le mot "dimension" désignant le fond indéfini des conditions de possibilité propres à chacun de ces objets, il est logiquement impossible, ici, de dénombrer moins de dimensions que d'objets. Objets et dimensions sont déterminés, produits les uns par les autres, dans une relation dont chaque réalité tire sa définition même; sauf à donner de ces réalités une définition ambigüe, mathématiquement non pertinente, comme c'est le cas dans la représentation courante qui ne compte dans l'espace que trois dimensions, où l'on entend par "dimension" une réalité qui peut être parcourue par un quelconque instrument de mesure, alors qu'il n'entre pas dans la nature d'une dimension de pouvoir obligatoirement l'être.

 

*

 

Il est possible de ressaisir le principe de cette méthode dans un cadre épistémologique moderne et rigoureux, qui est la théorie de la forme logique de Granger. Dans le système de Granger, la relation à partir de laquelle est défini tout contenu de science mathématique, est précisément la liaison entre une opération de pensée, (pour nous, un mouvement de la tétractys, une application), et un objet de pensée : l'objet mathématique qui est défini à chaque nouvelle application. C'est exactement le sens qu'il faut attribuer à la sentence pythagoricienne : "Une figure, un pas." A chaque objet défini, correspond une opération de pensée qui est quantifiée et engrammée de façon rigoureuse. Ainsi, dans la construction des objets géométriques, les 4 objets premiers sont d'abord construits synthétiquement, comme dans l'illustration ci-dessus, en utilisant les dix points de la tétractys, puis analytiquement - construction à 24 unités-points -, au moyen cette fois des factorielles des quatre premiers nombres.

  

 

1x1         2x1             3x2x1               4x3x2x1         

 

 

Granger appelle dualité cette corrélation, qui est une relation de cogenèse, de coengendrement, entre une opération mathématique, et un objet mathématique.

Quant à l'archétype de cette relation, sa formulation la plus générale, elle est à rechercher, selon toute apparence, dans la dualité des solides réguliers, qui sera évoquée au chapitre suivant.

 

*

        

A nos yeux, il n'y a que dans la mathématique pythagoricienne que cette méthode de définition conjointe des objets et des opérations mathématiques - méthode dont la réquisition est contenue de façon implicite, pour Granger, dans la notion bien comprise de dualité, - s'avère applicable de façon immédiate, et généralisable à l'ensemble du domaine de la mathématique; sans qu'il soit nécessaire pour cela d'ajouter une abondance de matériel nouveau aux axiomes élémentaires de l'arithmétique et de la géométrie classiques.

Pour le comprendre, il faut, en revanche, se poser la question de ce qu’est l’acte premier, l’acte fondateur de la mathématique.

Et pour éclaircir cette question, dont les racines sont historiques, il n'y a pas d'autre moyen que de revenir aux définitions qui ont été données, dès la plus haute antiquité, de l'objet le plus élémentaire de la géométrie : le point.

Dans cette perspective, comparons le début d’Euclide avec le début de Pythagore.

 

 

Le point euclidien

 

Euclide :

"Le point est ce qui n'a pas de partie".

On veut déjà donner une définition logique. On veut définir l'élément premier à partir d'un lieu de la science qui est ultérieur à lui, puisque c'est lui, le point, qui doit permettre de construire tout le reste. On est déjà dans la conception des modernes, où tout doit être produit à partir de ce qui vient en dernier : la logique.

Or la logique n'est que le vide dont la mathématique est le plein; elle n'est que la forme dont la mathématique est le contenu; elle est incapable de produire un contenu par ses ressources propres.

A l'évidence, la proposition d'Euclide constitue au mieux une définition logique du "zéro" géométrique, ou du bord topologique d'un objet. Ainsi, si l'on considère par exemple un segment, la proposition d'Euclide ne peut, en aucune façon, désigner le premier point de ce segment, mais uniquement le "rien" qui est juste avant et à côté, qui est au contact immédiat de sa "peau" si l'on peut dire; autrement dit la bulle de vide dont ce point s'est précisément soustrait, en tant qu'unité.

Dans la mesure où tout point peut être développé, par projection, dans une indéfinité de directions de l'espace, il paraît hautement risqué de soutenir, comme Euclide, que ces différentes possibilités qui sont toutes constitutives de sa nature, puissent ne pas correspondre à différentes parties de ce point. De fait, la proposition d'Euclide conduit rapidement à des conséquences absurdes.

Si, à partir d'un point, on commence à tracer, dans toutes les directions de l'espace, une série indéfinie de droites émanant de lui, et si en cours de route, on retranche de ce processus ce point lui-même, le "trou" formé au sein du continuum adopte progressivement la structure d'une bulle ou d'un petit sphéroïde; toutefois le contour de ce sphéroïde ne saurait être complètement défini avant que l'ensemble des rayons émanant du point aient été tracés, - ensemble qui se perd bien évidemment dans l'indéfini. D'ici là, la forme du sphéroïde ne sera donc qu'en partie définie. Or, comment une chose qui n'a pas de partie pourrait-elle être en partie définie?

Voilà que nous avons nettement distingué, dans le point, au moins deux parties, une qui est déjà définie, et une qui ne l'est pas encore; mais on comprend que, par induction, ce raisonnement nous contraint à distinguer dans le point une indéfinité de parties, dont chacune est individuellement bien définie par le bord intérieur de chacun des rayons aboutissant à ce point. Le fait que ces différentes parties ne puissent être distinguées au sein du point lui-même par un acte de discrimination spatiale, pour la raison qu'elles s'y trouvent toutes "repliées", confondues et réunies "au même endroit", n'implique en aucune manière qu'elles n'existent pas.

La formule d'Euclide : "ce qui n'a pas de partie" équivaut donc à dire : "ce qui ne peut être développé dans aucune direction"; ce qui est toujours une définition du vide logique ou du zéro géométrique.

Autrement dit, Euclide confond le point avec l'interstice logique purement virtuel, et rigoureusement nul, qui se situe topologiquement entre deux points.

Celui qui énonce : "Il existe un ensemble, appelé zéro, qui ne contient pas d'ensemble", ne fait à l'évidence que répéter la proposition : "Le point est ce qui n'a pas de partie." Comme la proposition d'Euclide, la définition du zéro qui, dans certaines versions de la théorie des ensembles, présente cet "ensemble vide" comme l'ultime contenu de la mathématique, sur lequel s'appuie la définition, ontologiquement ultérieure, de l'unité, (elle même définie comme le premier ensemble qui contient zéro), est sans consistance mathématique. Sans même être fausse, elle ne peut, par sa nature, donner matière à aucune mathématique digne de ce nom.

Ces deux propositions qui, dans leur compréhension juste, désignent respectivement le "zéro" géométrique et le "rien" arithmétique, (deux notions qui, en mathématique pythagoricienne, coïncident elles-mêmes dans celle du vide logique, qui en est la réunion synthétique), ne sont pas consistantes mathématiquement; parce que l'on n'a en rien réussi à produire l'élément premier de la mathématique, lorsqu'on s'est contenté de définir l'une de ses conditions de possibilité, d'ailleurs particulière, en ce qu'elle ne concerne, dans chaque cas, que l'un de ses aspects.

D'une façon plus générale, le point commun à de nombreuses approches modernes de la mathématique, qu'elles soient logicistes, ensemblistes ou axiomatisantes, aura été d'admettre comme "pari" ou comme "foi" scientifique originelle, le postulat que la mathématique est une phrase, que son être consiste dans une phrase, et que donc on peut le présenter dans une phrase, une proposition logique; présupposé qui était déjà manifestement celui d'Euclide. Or l'être de la mathématique ne peut pas consister dans une proposition logique, (comme il sera montré plus loin de façon évidente), parce que la mathématique ne devient une proposition logique qu'à partir d'un certain moment, qu’on qualifiera volontiers de moment opportun. Et il est impossible de dégager, de définir correctement ce moment opportun, si l'on n’a pas compté les différents mouvements qui ont dû être accomplis auparavant.

Si l’on compte à l’envers, - la manie des modernes, - ou si l'on essaie d'engendrer les premières opérations à partir des dernières, on échouera à chaque fois; et l’on parviendra toujours à des conclusions du genre : "Ce sont les irrationnels qui engendrent les rationnels".

Voilà quelques unes des raisons qui peuvent expliquer que le moment logique, - le gnomon - soit resté jusqu’ici inaccessible à l’intelligence des modernes.

 

 

Le point monadologique ou "arithmo-géométrique" pythagoricien

 

Début de Pythagore :

Dix points sont présentés dans la pensée :

 

 

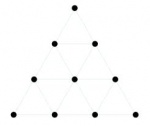
Pythagore est conscient que l'atome, l'élément premier de la géométrie, ne peut être défini par rien de plus originaire que lui-même, sans tomber dans d'insolubles paradoxes,  mais qu’il peut seulement être produit, montré, présenté dans la pensée. Encore n'est-ce possible qu'en l'articulant sous la forme d’une structure, d’un champ. Ce n'est que de la considération  des relations existant entre ces points, telles que symétries ou homothéties, qu'une définition plus précise de l'élément, ou de l'objet premier pourra se dégager; et celui-ci reçoit alors un statut bivalent, à la fois arithmétique et géométrique, qui est celui d'"unité-position", ou "unité ayant position".

De cette manière, on évite de construire la mathématique, comme Euclide, à partir d'une définition qui n'a pas de sens mathématique. La force de la mathématique pythagoricienne consiste toute entière dans cette sagesse, dans cette « prudence » du commencement. Mais aussi dans l'application rigoureuse, jusqu'à l'échelle la plus élémentaire, de la règle qui consiste à définir les objets mathématiques, à partir des seules opérations de pensée qui les engendrent. Une figure (un objet), un pas (une opération) : et l’on quantifie. 

Un point de l'espace, un coup de temps.

Une position du continuum, une unité arithmétique.

Une monade.

 

 *

 

Au fondement de la pensée pythagoricienne, il y a cette conviction que l'essentiel, en mathématique, ne peut être évoqué que de manière allusive et métaphorique, - que ce puisse être en image ou en mots ne changeant, fondamentalement, pas grand chose au problème; - et cela, au moyen d'une balance très prudente entre "ce qu'il nous importe profondément de montrer" et "ce qu'il est réellement possible de faire".

La science, pour Pythagore, consiste dans un rapport réfléchi entre le visible et l'invisible, entre le dicible et l'indicible, qui d'une part, lui impose d'intégrer dans ses méthodes, dans sa façon de faire, le problème des limites concrètes de la représentation, qu'elle puisse être figurale, symbolique, ou langagière, et d'autre part,  lui impose d'installer ou d'instituer, dans ses axiomes, à côté de la dimension du défini, (qui est la dimension de ce qui importe mathématiquement, de ce qui est déjà réuni, recueilli et connu dans le "secret", la certitude ou la foi de l'intelligence, et sur lequel va s'appuyer avec une confiance aveugle tout le reste : "les points sont équidistants", "au nombre de dix", "distribués en symétrie hexagonale", "forment un triangle équilatéral", etc.), la dimension de l'indéfini, de l'à peu près et du vague; dimension que la mathématique ne refuse ni ne refoule aucunement par principe, mais qu'elle assume au contraire régulièrement dans sa pratique quotidienne, et que la mathématique pythagoricienne se contente de revendiquer de façon plus affirmative, sur un plan plus radical, qui est celui des principes fondamentaux.

C'est dans l'assomption de cette limite absolue de la représentation que réside l'originalité de la tétractys. Sur le plan du langage logique, l'équivalent du point monadologique ou "arithmo-géométrique" pythagoricien, ce point qui a comme propriétés apparentes d'être plat et assez gros, et comme propriété essentielle d'être de dimension indéfinie, n'est donc pas l'identité, - identité qui, en elle-même, n'est susceptible d'aucune représentation, puisque toute représentation, toute forme, suppose un processus de différenciation matérielle, qui est contradictoire avec l'identité, - mais plutôt une sorte de reflet de l'identité, déjà forcément diffracté. 

Car le langage logique ne contient pas, lui non plus, la possibilité d'une définition de l'identité sur laquelle s'appuie sa propre consistance, et dont il ne peut faire mieux que de produire, au commencement des choses, des exemples élémentaires différenciés tels que "p", "q", qui par la suite serviront de référence. Toute proposition logique qui tenterait de définir l'identité ne peut, par nature, qu'être contradictoire ou inconsistante; et donc, ne peut pas être au sens propre une proposition logique, mais, au mieux, une image ou une métaphore.

Ainsi, la logique prédicative connaît deux images, - forcément paradoxales, puisque l'identité véritable est ce qui ne tolère, quant à soi, aucune forme d'"altérité", - non pas précisément de l'identité, mais de deux différents mouvements vers l'identité, mouvements dont l'un est ouvrant ou centrifuge, le connecteur "ni..., ni..." ("une tache ni bleue ni triangulaire") et dont l'autre est fermant ou centripète, le connecteur "et", qui attribue deux propriétés (et pas davantage, sauf à renouveler l'opération) à un être ou objet unique, ("une tache rouge et rectangulaire"). ⁽¹⁾

 

NI......................ET.....................NI

 

De la même manière exactement, le point monadologique pythagoricien pourra, très avantageusement, être considéré comme un processus "fermant-ouvrant", ou "inhibiteur-activateur", comparable au mécanisme d'un parapluie, (en langue mathématique, un tenseur binaire, quantitativement indéfini), dont l'axe "ni..., ni..." ci-dessus représenterait le diamètre apparent, et la position "et" la coordonnée mathématique, définie par la relation que ce point entretient avec les autres membres de la constellation, quelque soit la méthode choisie pour paramétrer cette dernière.

Là réside, peut-être bien, le fond de la foi mathématique, dans la confiance que l'identité "insaisissable" se repose, très paisiblement, dans la réunion synthétique des connecteurs "ni..., ni..." et "et".

L'essentiel n'est ni la propriété "a", ni la propriété "b", (propriétés qui sont néanmoins, par hypothèse, les seules que l'on sache ou puisse concrètement montrer, et qui sont précisément toujours des propriétés telles que "plat", "noir", "rond", "assez gros" ou "à gauche"), mais l'être qui, sans être deux, les contient l'une et l'autre "en même temps", ("à la fois" ou "ensemble"), et n'est rien d'autre que leur compossibilité même.

Formule qui n'est toujours pas une définition de l'identité, mais qui est en revanche une définition en mode logique de la synthèse, en tant que méthode de régression intellectuelle progressive, prudente et patiente, du visible indéfini à l'invisible défini, d'abord, puis, de ce connu, de ce défini, à l'ensemble des possibilités mathématiques qui sont nées avec lui, parce qu'elles sont contenues dans sa définition ou dans son être même; - méthode que l'on peut caractériser par des expressions telles que "retroussement", ou "développement  continu", dans laquelle, à aucun moment, ne peut être perdu le contact avec l'image installée au début dans la pensée, et restée depuis présente au fond de celle-ci, comme une pierre de témoignage. ⁽²⁾

 

 

*

 

Ce sont d'autres définitions de la synthèse, plus mathématiques celles-là, qui seront évoquées au chapitre suivant.

 

 

 

 

⁽¹⁾ L'apparence paradoxale de ces formulations, en tant qu'elles se rapportent à l'identité, à l'unité, et finalement à l'être, provient de ce que, dans un cas,  l'identité, ou l'unité, est représentée comme "ce dans quoi peuvent rentrer, ou se réunir deux ("autres") choses"; tandis que, dans l'autre cas, cette même identité, cette même unité est représentée négativement comme "ce qui peut être séparé, distingué radicalement de deux ("autres") choses". La nature même du langage fait qu'il est impossible de s'approcher davantage d'une définition correcte de ce dont il s'agit; alors que ce dont on voudrait parler, et qui peut seulement être objet de foi ou d'intuition, consiste précisément dans la réunion synthétique et non contradictoire des idées contenues dans ces deux représentations.

L'identité est comparable à l'enfant de deux parents, mais un enfant qui, après s'être différencié de leurs deux corps, continuerait d'être une partie intégrante de chacun d'eux, un élément ou un membre à part entière de leurs personnes. Un enfant de cette sorte n'est ni son père, ni sa mère; mais à la fois son père et sa mère.

L'enfant est l'unité et l'identité. L'enfant est la monade qui, selon la tradition, "contient la dyade".

 

⁽²⁾ Le point pythagoricien est suffisamment défini, mais pas trop; et c'est en cela qu'il représente essentiellement du devenir et du "travail".

 

 

 

  

 

LE DEVELOPPEMENT CONTINU

 DE LA TETRACTYS

  

  

par Guillaume DENOM

  

 

 

  

 

 

 I.    LA LOI DU GNOMON

 

"L'ensemble des gnomons du carré, est égal à l'ensemble des gnomons du triangle équilatéral, est égal à l'ensemble des nombres entiers Impairs."

 

                                  

 

La loi du gnomon : G(c) = G(t.e) = I,  exposée, sur notre premier blog, dans les trois premiers articles de la deuxième section, est une loi importante de la mathématique. Son ancienneté, dans les termes où elle formulée ici, est attestée par divers témoignages, comme celui de Jean Philopon, selon qui les anciens appelaient "gnomons" les nombres impairs. S’il peut paraître étonnant qu'elle ne soit pas reconnue à sa juste valeur, et plus encore que, sous sa forme rigoureuse, elle semble même inconnue de la littérature mathématique contemporaine, il y a en réalité à cela des raisons précises et pour ainsi dire "naturelles".

La loi du gnomon est une loi synthétique, dont les applications se répartissent entre trois domaines de la mathématique : arithmétique, géométrie, logique. Pourtant, ce n’est pas une loi générale, c'est-à-dire qu’elle ne surplombe pas ces différents domaines à partir d’une position extérieure et dominante, mais, bien au contraire, elle agit à l’intérieur de chacun d’eux d’une manière spécifique.

La mathématique moderne n'est guère synthétique. Son geste le plus caractéristique est la généralisation, geste qui est bien différent de la synthèse, et en quelque manière opposé; puisque, si la synthèse est une action qui consiste à abstraire les propriétés intrinsèques que différents objets détiennent en commun, la généralisation consiste, elle, à partir d'une forme d'objet particulière (telle que la fraction, le nombre décimal, etc.), à définir une extension de cette forme ou formule particulière à l'ensemble du domaine d’objets dont elle dépend, par une action qui se qualifie elle-même de "conventionnelle". Par exemple : « tous les entiers peuvent être considérés comme des nombres décimaux »; ou encore : « les entiers peuvent être considérés comme des fractions. » 

En résumé, si la synthèse consiste en une connaissance sur des objets, la généralisation, elle, consiste en l'exploitation intensive d'une forme d'objet, - forme tenue en définitive pour l'"objet" le plus essentiel, alors même que, par sa nature, elle ne représente pour l'objet authentique dont elle est le moule ou la matrice - dans notre exemple : le nombre - qu'une possibilité de formulation parmi une indéfinité d'autres.

La généralisation, lorsqu'elle est pratiquée, comme elle l'est dans la mathématique moderne, de façon pour ainsi dire machinale, entraîne une double tendance de l'esprit mathématique, d'une part, à considérer comme "première", au sens de plus ontologique, la forme d'objet qui est la plus tard venue, ou la plus récemment définie, telle que le nombre réel ou le nombre complexe, d'autre part, à considérer qu'il n’existe pas de naturalité mathématique, mais que la mathématique est une façon de définir les choses qui est "conventionnelle" par essence, qui peut être "librement choisie".

 

Mais sans plus attendre, commençons par détailler les trois premiers domaines d’application de la loi du gnomon.

1. En arithmétique, la structure du gnomon est la triple articulation, intégralement coordonnée, du nombre impair (gnomon), du nombre entier (côté du polygone), et du nombre carré  (polygone gnomonique).

 

 

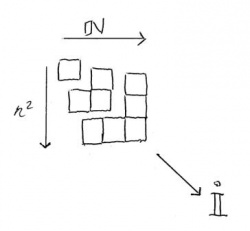
Dans cette structure, on a, sur l’axe horizontal, (ou plus généralement, sur le côté du polygone), la série indéfinie des nombres entiers ordinaux (1, 2, 3, 4, ...) ; sur la diagonale (ou, pour le triangle, la médiatrice verticale), la série des impairs cardinaux (1, 3, 5, 7, ...) ; enfin, sur l’axe des résolutions, la série des nombres carrés ordinaux : (1, 4, 9, 16,...) ; en précisant que, dans la logique du gnomon, on définit comme cardinaux les nombres qui possèdent une existence individuelle, en ce que chacun d'eux survit à la suppression de tous les autres membres, inférieurs et supérieurs, de la série à laquelle ils appartiennent, et ordinaux, les nombres qui ne subsistent qu'au sein d'une chaîne, ou d'un ensemble, dont chaque élément est une partie constitutive de son successeur. La structure arithmétique du gnomon est donc une application biunivoque qui, à chaque cardinal impair, associe une paire d'ordinaux, respectivement entier et carré  : I → (E, C), cette application permettant de représenter chaque objet gnomonique par un triplet de nombres. Si, par exemple, on assigne à l'impair la position médiane (par analogie avec la fonction qu'il exerce dans l'objet géométrique, où l'axe de symétrie directeur de la structure, qui est celui de la progression des gnomons impairs, est déterminé par son angle d'origine, dont il est la bissectrice), et à l'entier la position initiale, la série indéfinie des objets gnomoniques peut être formulée par une matrice (E, I, C), dont les premiers triplets sont : (1, 1, 1); (2, 3, 4); (3, 5, 9); (4, 7, 16); ... - ce système de coordonnées étant, rappelons-le, consistant et complet aussi bien pour le triangle que pour le carré gnomonique. ⁽¹⁾

  

2. En géométrie, le polygone gnomonique de rang 2, triangle ou carré, est la formulation minimale (ce qui implique : quantifiée) du principe géométrique qui est recouvert par les notions modernes d’endomorphisme et d’autosimilarité; et qui est, en langage courant, la propriété d'un objet, d'être constitué de parties semblables au tout qu'elles composent. 

 

polygones gnomoniques de rang 2

 

 3. La théorie du gnomon est la plus fondamentale des théories mathématiques contenant une application biunivoque des notions de nombre entier et de figure entière, et pour cette raison elle est l'interface la plus étroite qui puisse exister entre arithmétique et géométrie. Le gnomon est un objet mathématique dans lequel arithméticité et géométricité sont coproduits : car le gnomon est un nombre; le gnomon est le nombre de figures, que l'on doit ajouter à une figure, pour la reconstituer. En tant qu’interface la plus étroite possible entre nombre et figure, entre arithmétique et géométrie, le polygone gnomonique de rang 2, triangle ou carré, est le plus petit espace logique qui puisse exister : en précisant là encore, que l’on parle d’un espace quantifié, permettant une construction quantifiée de la logique, telle que la logique des tables de vérité. 

 

  4. C’est seulement dans un quatrième temps, après avoir détaillé la liste de ses applications dans chacun des domaines de la mathématique, que la loi du gnomon peut être envisagée synthétiquement, et que peut être évaluée sa place particulière dans l’appareil de la mathématique pythagoricienne.  La théorie du gnomon permet de donner un sens précis à la notion de tétractys : "clôture à quatre", ou si l’on préfère, "clôture quaternaire"; cette clotûre correspondant à la quantité d'espace nécessaire et suffisante pour que puisse se déployer la structure du gnomon, dans laquelle : graine + gnomon = 4.

La tétractys et le gnomon se déduisent en effet l'un de l'autre de la façon la plus simple, en ce que les étages de la structure triangulaire de la tétractys correspondent, biunivoquement, aux distances qui s'établissent entre les centres des blocs, au fur et à mesure que se remplit le gnomon du carré. Autrement dit, la même action qui, dans le gnomon du carré, se développe sous forme ordinale, est récapitulée, dans la tétractys, sous forme cardinale.

Sous cette armature logique, la notion de tétractys devient une notion mathématique utilisable, rendant possible une véritable mise en ordre des concepts mathématiques pythagoriciens. 

La notion de clôture est indispensable, en réalité, pour comprendre l'unité synthétique de ces différents concepts, et par suite, pour exposer de façon rigoureuse les applications contenues, sur notre premier blog, dans les trois premiers articles de la première section, à savoir : tétractys = base arithmétique (inclues dimensions décimale et négative) ;  tétractys = dimensions de l’espace et objets premiers de la géométrie ; tétractys = accords musicaux = noyau du système des médiétés, (en deux applications).

  

Par hypothèse, un traité, ou une théorie, de mathématique pythagoricienne, est un traité, ou une théorie, dont tous les axiomes sont déduits ou dérivés des propriétés mathématiques de la tétractys.

  

La mathématique pythagoricienne n'a a priori besoin d'aucune autre notion mathématique que celles qu'elle produit elle-même. Dans l'absolu, même les signes utilisés devraient être justifiés par la tétractys. Les chiffres arabes pourraient êtres remplacés par des tétractys à points triangulaires, les opérations logiques par les logons binaires, etc. En pratique, c'est évidemment difficile et un peu contre-productif, mais dans la visée qui est la sienne, la mathématique pythagoricienne n'utilise pas de signes « conventionnels », mais produit les signes dont elle a besoin.

Ceci n'est qu'un horizon, mais qui peut servir de guide. 

Au départ, la tétractys est une idée qui n'est pas définie, mais qui est montrée, qui est présentée dans la pensée. La mathématique pythagoricienne ne fait que répéter indéfiniment ce geste premier, ou plutôt le prolonger, le poursuivre par un développement continu.

La mathématique pythagoricienne est le développement continu d'une structure constante qui est la tétractys, dont la fonction est de déplier successivement, application par application, toutes les parties de la mathématique. Dans l’idéal, toutes les applications de la tétractys peuvent s'enchaîner par un mouvement continu, entièrement coordonné, au moyen d'un seul et unique opérateur topologique qui est le retroussement d'une structure : mouvement par lequel le dessous passe au dessus, et le dedans au dehors, par une poussée continuelle, et qui peut être illustré, de façon très intuitive, au moyen d'objets géométriques tels que l'hypercube. La question est complexe, mais, dans l'idéal, la présentation écrite de la mathématique pythagoricienne n'est pas la forme préférable. Une animation en 3D avec une voix off serait plus parlante, parce qu’elle permettrait d'avoir, au lieu d'images arrêtées, un mouvement réellement continu où l'on ne perdrait jamais de vue la structure ponctiforme à 10 points produite au départ. 

  

 

⁽¹⁾ Cette "triangularité" arithmétique semble apparenter  la structure du gnomon à d'autres structures arithmétiques connues, comme par exemple la célèbre formule de Ramanujan associant les nombres pi et e, dans laquelle on retrouve, sur l'axe horizontal, la série des impairs; sur l'axe vertical, la série des entiers; et du côté de la résolution, la racine carrée, opération inverse de l'opération "carré".        

                                                                                       Côté résolution : la racine carrée

 

 

 

 Axe horizontal : série des impairs (1, 3, 5, 7, …)          Axe vertical : série des entiers : (1, 2, 3, 4, ...)