Rectangle de Fibonacci

et triangle d'or de Penrose

 deux applications géométriques de la médiété Nicomaque 10

par Guillaume DENOM 

            Bien que plusieurs auteurs aient déjà signalé que la « suite de Fibonacci » était une notion connue et définie depuis l’antiquité dans le cadre du système des médiétés, la littérature mathématique contemporaine continue d’utiliser  l’expression « suite de Fibonacci », au mépris de la réalité historique, pour désigner cette notion. La plus ancienne trace écrite de cette notion figure dans  l’Introduction arithmétique de Nicomaque de Gérase, soit plus d’un millénaire avant Fibonacci; en outre, Nicomaque nous précise qu’il n’en est pas lui-même le découvreur, sans indiquer à quelle source il l’a puisée.

            Si cette occultation historique est fâcheuse, ce n’est pas pour des raisons de « propriété intellectuelle » qui n’ont, en pythagorisme, aucune espèce d'importance, mais pour la compréhension même de la notion dont il s’agit.

            En effet, il n’existe pas de définition plus synthétique, ni plus profonde, de la suite de Fibonacci, que celle qui est donnée dans le cadre du système des médiétés, où elle ne constitue qu’un cas particulier, ou, si l’on préfère,  un élément, d’un ensemble qui en compte 12.

            Avant d’aller plus loin, rappelons que, dans le système des médiétés,  trois nombres : a, b, c, sont en proportion « de Fibonacci » (c'est-à-dire en « médiété Nicomaque 10 ») si et seulement si ils satisfont entre eux la relation :

(c - b) = a

(c - a)    b

*

            Dans son Dossier Pythagore, Pierre Brémaud signale une propriété très intéressante des nombres de Fibonacci.

            « Terminons cette liste des propriétés remarquables de la suite de Fibonacci par celle-ci :

            « La figure suivante devrait convaincre le lecteur de la justesse de cette relation et de la beauté de l’arithmétique géométrique modo pythagorico. »

Pierre Brémaud, Le dossier Pythagore, p 290.

            La construction de M. Brémaud est en effet des plus intéressantes, puisqu'elle revient à définir une relation constante entre la suite des nombres de Fibonacci et celle des carrés gnomoniques qui leur correspondent, relation constituant une application importante entre la théorie des médiétés et celle du gnomon.

            Reconnaissons, toutefois, que cette construction aurait été encore plus belle et pertinente, si M. Brémaud avait disposé ses carrés en suivant la progression d’une spirale logarithmique, comme dans la figure ci-dessous :

            Dans cette application de la médiété au carré gnomonique, on remarque, en particulier, que les hypoténuses correspondantes aux carrés successifs de la suite de Fibonacci, se trouvent, elles aussi, en proportion « de Fibonacci ».

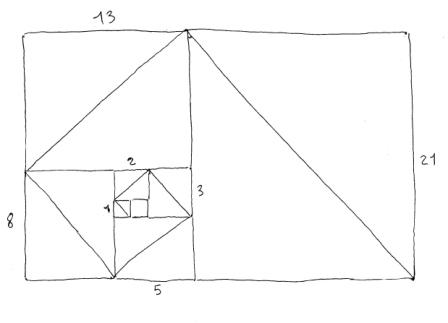
           Si l’on prend pour exemple les hypoténuses correspondantes aux carrés de côtés 2, 3 et 5, on vérifie que :

(rac 50 – rac 18)  =  rac 8        =   2

(rac 50 – rac 8)        rac 18           3

            Et l'on constate que le rapport a/b qui est le rapport mineur de la médiété (situé à droite du signe égal) est égal au simple rapport des côtés des carrés utilisés, - tout cela en application évidente du théorème de Pythagore.

            Enfin, cette construction permet de tracer la spirale logarithmique correspondante à la suite des carrés, spirale rendue célèbre par ses multiples applications « florales » (pissenlit, artichaut, tournesol, etc).

*

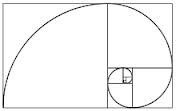
            On peut remarquer que la structure de la médiété Nicomaque 10 est constituée, dès l'instant où l'on a disposé les trois premiers carrés (carrés gnomoniques  de rangs 1, 1 et 2), formant ensemble un premier "rectangle de Fibonacci". Le rapport entre la longueur et la largeur du rectangle peut, dès cet instant, être considéré comme une première approximation du nombre d'or, certes grossière, mais qui ne cesse ensuite de se préciser à mesure que la taille du rectangle augmente.

            Dans la littérature moderne, la contribution la plus importante, concernant cette médiété Nicomaque 10, me semble être celle de Roger Penrose, avec ses fameux "pavages de Penrose".

            On peut dire que la démarche de Penrose est en quelque manière inverse de celle qui est illustrée dans la figure ci-dessus. Alors que, dans la figure ci-dessus, le nombre d'or est la limite vers laquelle tend la croissance du rectangle, dans un pavage de Penrose, ce même nombre d'or est la structure invariante que l'on pose au départ, sous la forme d'un premier triangle d'or, triangle qui, par des divisions successives, engendre un pavage continu non périodique, dans lequel on retrouve la suite des nombres de Fibonacci.

            Le "rectangle de Fibonacci" et le "triangle d'or de Penrose" peuvent sans doute être considérés comme les objets géométriques les plus fondamentaux que l'on doive associer à la médiété Nicomaque 10. Entre ces deux objets s'opère un retournement, un retroussement, par lequel toute la nature mathématique se trouve transformée. En effet.

            Alors que, dans le rectangle de Fibonacci, la suite de Fibonacci est une fonction de croissance, elle est, dans le triangle de Penrose, une fonction de division. Alors que le nombre d'or est, dans le rectangle de Fibonacci, le nombre correspondant à la position de l'infini, il est, dans le triangle de Penrose, le nombre correspondant à la position "1". Alors que ce qui est "Fibonacci" dans le rectangle de Fibonacci est le nombre de carrés (les nombres de Fibonacci  correspondant au nombre de carrés "atomiques" de valeur 1 que l'on peut dénombrer sur les côtés des rectangles successifs - largeur et longueur), ce qui est "Fibonacci" dans le triangle de Penrose est le nombre de triangles  (obtus et aigus). Le rectangle de Fibonacci contient l'infini, dans ce sens que deux rectangles de Fibonacci ne sont jamais semblables au sens mathématique (le rapport largeur/longueur n'est jamais le même), bien qu'ils soient de moins en moins différents; le triangle de Penrose contient l'infini sur un mode qui est celui de la non-périodicité, c'est à dire que le motif dessiné par un pavage de Penrose ne présente jamais de règle de répétitivité continue, de sorte qu'il est impossible d'en construire l'ensemble au moyen de la réplication d'une partie quelconque.

            A ces diverses différences-symétries entre les deux structures, on peut ajouter cette dernière, plus profonde. Alors que, dans le rectangle de Fibonacci, la médiété Nicomaque 10 est une fonction de l'espace, qui s'accomplit dans le temps, dans le triangle de Penrose, la médiété Nicomaque 10 est une fonction du temps, qui s'accomplit dans l'espace.

Triangle d'or de Penrose

            La progression du nombre de triangles d'or, aigüs et obtus, est celle de la suite de Fibonacci. Au bout de quelques étapes, on obtient toutes les autres pièces permettant de construire des "pavages de Penrose", à savoir la paire  (fléchette / cerf-volant), et la paire (losange gras / losange maigre). Le triangle de Penrose, constitué de triangles d'or aigüs et obtus, est donc la formule la plus générale, dont dérivent par composition toutes les autres.

  *

            Concluons par deux remarques à caractère plus aphoristique.

            Situation du pythagorisme.

            Penrose considérait ses pavages comme une récréation mathématique, et n'attribuait pas à ce travail une importance comparable à celle de ses travaux mathématiques "sérieux". De nos jours, l'impact de cette découverte sur la science en général apparaît, au contraire, plus important que celui de ses autres travaux. Ce malentendu est tout sauf anodin, et traduit la situation "problématique" qui peut être celle du pythagorisme dans la science contemporaine.

            Le devenir physique des idées mathématiques pythagoriciennes.

            Les pavages de Penrose ont une symétrie d'ordre 5, pentagonale donc, qui était jusque récemment considérée comme interdite dans l'ordre très rigoureux qui est celui des "systèmes cristallins". Un cristal de symétrie pentagonale était considéré comme une impossibilité, parce que le pentagone n'est pas une solution de pavage du plan (et donc, ne peut permettre de construire une facette cristalline). Dans cet ancien paradigme, la contrainte de continuité était associée à la contrainte de périodicité. Au début des années 80, des quasi-cristaux de symétrie pentagonale, présentant toutes les apparences d'un cristal normal, et répondant aux caractéristiques mathématiques d'un pavage de Penrose (continuité non périodique), sont réalisés de façon synthétique*. En 2008, on découvre que, ce que la chimie venait d'accomplir, la nature l'avait déjà réalisé : un quasi-cristal naturel de symétrie pentagonale, probablement d'origine extraterrestre, est découvert en Russie. Ces divers événements ont contraint les manuels de cristallographie à modifier leur définition du cristal, afin d'y intégrer les quasi-cristaux de symétrie pentagonale. Pourtant, la cristallographie pouvait être considérée jusque là comme un département achevé de la physique : édifice entièrement prisonnier des lois de la symétrie, formulées aujourd'hui dans le cadre de la théorie des groupes. La cristallographie est, de fait, une espèce de dimension "témoin" de la physique, interface parfaite entre la structure invisible : les arrangements d'atomes, et la structure visible : la facette du cristal, et son angle au sommet, pure matérialisation de la géométrie des polyèdres.

            Là encore, on n'est qu'à moitié surpris. Aujourd'hui comme hier, les idées mathématiques pythagoriciennes semblent affectées d'un certain "devenir physique". La mathématique pythagoricienne implique, parmi d'autres choses,  la recherche d'une certaine adéquation entre la nature mathématique, et la nature physique. Son objet la détermine à décrire, assez souvent, le genre de choses que la nature est susceptible, elle aussi, de réaliser.

*En 2011, Dan Shechtman s'est vu décerner le prix nobel de chimie pour ces travaux sur les quasi-cristaux.

 Quelques applications florales de la suite de Fibonacci

 Structure et aspect d'un quasi-cristal de synthèse

Météorite quasi-cristalline découverte en Russie en 2008

GLOSES  

      1. Les médiétés de 1 à 0

     On a vu que la médiété N1 pouvait être définie comme saturée sur un plan sémantique et logique, mais il est également possible de la reconnaître comme saturée sur un plan purement mathématique, puisque le rapport mineur de cette médiété a une valeur constante de x/x = 1, valeur qui coïncide avec l'extension maximale que peut prendre le rapport mineur d'une médiété, les rapports mineurs des autres médiétés pouvant tous s'exprimer par des rapports inférieurs à 1. Dans cette perspective, il peut être intéressant d'élargir notre définition habituelle de la médiété, en définissant le système dans N inclu zéro, et en stipulant qu'une médiété est une relation entre 3 nombres A, B, C, tels que A inférieur ou égal à B inférieur ou égal à C, dans laquelle deux de ces nombres sont entre eux dans le même rapport (mineure) que deux de leurs différences (majeure). On obtient alors 5 niveaux étagés entre 1 et 0.

 
Niveau 1. La position de référence est donc celle, saturée, de la seule médiété N1 (dite arithmétique) dont le pprm (plus petit rapport mineur possible) est égal à 1.

          Niveau 2. Un ensemble de 5 médiétés dont le pprm est égal à 2/3. Ce sont les médiétés N6, N7, N8, N9 et T12. Ces médiétés, auxquelles je ne connais pas d'application géométrique remarquable, donnent l'impression de fonctionner toutes de la même manière et de pouvoir être reliées par une équation commune, de manière à ne former qu'une seule supermédiété.

      Niveau 3. Quatre médiétés dont le pprm est égal à 1/2. Ce sont la médiété "géométrique" N2, les médiétés  N4 et N5, ainsi que la médiété T11, que l'on a déjà examinée en raison de son absence d'intérêt mathématique, son adoption se résumant à intégrer dans le système un axiome d'existence du nombre zéro.

          Niveau 4. Une seule médiété N3, (dite "harmonique"), dont le pprm est égal à 1/3.

           Niveau 5. Dans cette formulation, la position "saturée" qui répond symétriquement à l'autre extrémité du système (où l'envergure est "maximale", c'est à dire égale à 1) est donc occupée par la seule médiété N10 ("de Fibonacci"), dans laquelle le pprm est égal à 0/1 = 0. Puisqu'en effet, notre définition élargie permet d'admettre comme "plus petite solution possible" de la médiété la solution (0, 1, 1), et par suite comme pprm le rapport 0/1. Sur le plan logique, on ne peut donc pas avoir moins de 5 médiétés, semble-t-il.
  

Précisons que, dans ce raisonnement, on appelle pprm le rapport mineur simplifié, contenu dans la plus petite solution entière d'une médiété; c'est ce rapport qui comporte 5 degrés d'obturation entre 1 et 0. Ainsi, les médiétés du niveau 2 ont, dans leur plus petite solution entière, un rapport mineur égal à 4/6  ou 6/9 (= 2/3). Sur la table des médiétés du blog, les plus petites solutions entières sont reprises de Nicomaque, chez qui elles ne sont pas forcément justifiées par une définition explicite. Pour la médiété "de Fibonacci", Nicomaque retient comme première solution le triplet (3, 5, 8), sans doute pour éviter le triplet (1, 2, 3) qui serait identique à N1. Nicomaque semble donc favoriser la première solution originale d'une médiété; mais rien n'interdit de reformuler la table des solutions à partir d'une définition plus moderne de la médiété, et en privilégiant non plus la première solution originale, mais la première solution possible. Dans ce cas, il paraît donc avantageux de définir le système pour A inférieur ou égal à B inférieur ou égal à C, de manière à intégrer toutes les solutions initiales de la suite de Fibonacci, et notamment les 4 solutions qui précèdent celle retenue par Nicomaque, savoir : (0, 1, 1); (1, 1, 2); (1, 2, 3); (2, 3, 5); ...

2. Obturation du rapport mineur. 
 

La relation logique M (médiété), est une relation biternaire : x/y = M (A, B, C), où x et y doivent être choisis parmi les termes A, B ou C, et où M est le rapport de deux soustractions entre ces trois termes. Dans cette relation, le rapport mineur x/y représente donc le "côté" binaire de la relation.

Dans le système défini plus haut, on peut représenter l'obturation du rapport mineur par l'inscription d'un trépied, ou d'un triangle équilatéral, dans le cercle-unité. Les 12 médiétés se répartissent alors sur 4 positions, puisque les positions de N1 (arithmétique) et N10 (Fibonacci) coïncident, à ceci près que N1 correspond au cercle plein, et "Fibonacci" au même cercle vide. Les positions des médiétés peuvent ainsi recevoir une formulation "angulaire" qui est quaternaire, mais en remarquant que l'angle de la médiété N2 (géométrique) est déterminé par la médiatrice verticale du triangle équilatéral. La structure biternaire est donc bien apparente, même lorsqu'on ne considère que le rapport mineur. L'axe vertical correspond au côté binaire, le trépied au côté ternaire de la relation.

3.  Table de correspondance

                Cet article, pourtant simple, a suscité beaucoup de confusions, et notamment l’idée surprenante selon laquelle il pourrait exister des termes manquants dans une fonction mathématique. Il a donc paru utile de dresser une table de correspondance entre les deux structures. 

                Il existe, bien évidemment, deux fois plus de rectangles de Fibonacci que de triangles de Penrose, puisque le rectangle de Fibonacci développe les nombres de Fibonacci par paires conjointes, alors que le triangle de Penrose développe ces mêmes nombres par paires disjointes. 

                La série des triangles de Penrose correspond uniquement aux étapes impaires de la série des rectangles de Fibonacci.  Dans le rectangle de Fibonacci, les nombres de Fibonacci correspondent au rapport de la largeur à la longueur (l/L). Le « rectangle de Fibonacci » de rang 1, est donc un « rectangle » de largeur zéro et de longueur 1, c'est-à-dire un segment de longueur 1. Le rectangle de  Fibonacci de rang 2 est un « rectangle » de 1x1, autrement dit le carré atomique de côté 1 (qui permet ensuite de calculer déductivement, visuellement, les valeurs de tous les carrés suivants).  Au rapport (largeur/longueur) du rectangle de Fibonacci, correspond, une fois sur deux, le rapport (triangles obtus/triangles aigus) qui décrit la composition du triangle de Penrose.

                On se convaincra, au vu de ce tableau, que les deux fonctions sont bien complètes, et parcourent la série entière des nombres de Fibonacci, de zéro à l'infini; en précisant que, dans cet article comme dans d'autres, on emploie, par commodité, le terme "infini" dans le sens hyperbolique qui est celui de la mathématique moderne, pour désigner différentes variétés de l'indéfini.

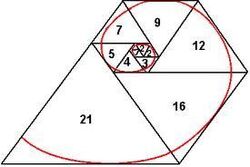
4. Pentagone de Padovan

Si on le considère maintenant, non plus sous le seul angle de sa relation avec la médiété Nicomaque 10,  mais d'un point de vue plus général qui est celui de la théorie des polygones gnomoniques, le rectangle de Fibonacci possède une structure jumelle qui est le pentagone de Padovan.

Alors que le rectangle de Fibonacci est formé de carrés gnomoniques, le pentagone de Padovan est formé de triangles gnomoniques. A chacune de ces structures sont associés une suite arithmétique et un nombre (irrationnel) remarquables (au nombre d'or, phi, de la suite de Fibonacci répondant le nombre "plastique", psi, de la suite de Padovan), ainsi qu'une spirale logarithmique. De la même manière que, dans le rectangle de Fibonacci, le rapport entre les côtés tend vers phi, dans le pentagone de Padovan, le rapport entre deux côtés successifs du pentagone tend vers psi.

La suite de Padovan, en revanche, ne relève pas de la théorie "classique" des médiétés à 3 termes, mais d'une théorie plus générale comprenant les médiétés à 4 et 5 termes, ou plus, domaine qui reste largement inexploré si l'on excepte l'étude, par Nicomaque notamment, de la médiété "parfaite", ayant pour plus petite solution le quadruplet (6-8-9-12).

La médiété ci-dessus, qu'on appellera médiété de Padovan, peut, par exemple, être définie comme une relation entre 5 termes : a, b, c, d, e, chacun étant inférieur ou égal* à son successeur, dans laquelle on a ces trois identités :

a + b = d

b + c = e

(a + e) = (c + d)

Les cinq termes correspondant aux cinq triangles gnomoniques qui sont suffisants pour délimiter la circonférence de n'importe quel pentagone de Padovan. Dans l'exemple illustré ci-dessus, les termes a, b, c, d, e, correspondent (pour le plus grand des pentagones) aux triangles gnomoniques de rangs : 7, 9, 12, 16 et 21.

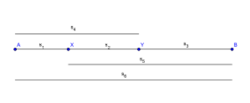
Gérard Cordonnier a défini cette médiété en utilisant la méthode euclidienne de division d'un segment en "extrême et moyenne raison", qui permet de définir le nombre d'or. 

Pour le nombre "plastique", le segment est divisé en trois parties, qui déterminent elles mêmes par combinaison trois autres grandeurs; ces six segments étant tous ordonnés en proportion géométrique. Gérard Cordonnier montre que la proportion géométrique est de valeur : "psi"; ce qui signifie que, tout comme une grandeur peut être "double" ou "triple" d'une autre, chaque segment est ici le "psi-uple" du précédent.**

On voit que les deux méthodes, géométrique et "algébrique", sont équivalentes, puisque tous ces rapports de grandeur sont déductibles des trois identités formulées plus haut. Les segments 1 à 5 correspondent aux termes (a, b, c, d, e) de la médiété, quant au sixième, il correspond au terme "f", terme qui est donc le "successeur immédiat" de la médiété, et qui est toujours égal à (a + b + c) comme cela ressort également de nos trois formules.

*La mention "inférieur ou égal" permettant, comme pour la suite de Fibonacci, de faire débuter la suite de Padovan à zéro, et d'attribuer pour valeurs au pentagone de Padovan de rang 1, le quintuplet : (0, 1, 1, 1, 2). La série se développe ensuite par quintuplets conjoints, le pentagone ci-dessus occupant  le rang 10.

**La très grande généralité de la médiété géométrique fait qu'elle joue ici le rôle de substrat, ou de "paradigme", dans la définition d'une médiété d'ordre moins primitif.

Références :

Pierre Brémaud : Le dossier Pythagore, Ellipses, 2010. 

Sous cet excellent titre, Pierre Brémaud a rédigé un livre qui, tout en offrant une synthèse accessible à un large public, ne se prive pas d'apporter audit dossier certains éléments originaux, parmi lesquels on retiendra, le choix étant difficile, son dossier mathématique, son tableau du pythagorisme à la période alexandrine, ou encore, sa discussion pleine de bon sens du problème de la prétendue "crise des incommensurables", dans laquelle il démasque, sinon une invention pure et simple des modernes, du moins une problématique dont la signification historique a été faussée, et "montée en épingle" à partir de quelques fragments mal interprétés.

Mario Livio : The golden Ratio, Broadway, 2002.

Marius Cleyet-Michaud : Le nombre d'Or, Que Sais-Je? PUF, 1972.

1 commentaire

•  

  5. Foi religieuse ou foi scientifique?

  Par zalmoxis dans le 20 Septembre 2012 à 09:22

   

   

  FOI RELIGIEUSE OU FOI SCIENTIFIQUE ?

    

  par G. Denom

    

      

   

              Ce texte est la synthèse de deux lettres que j'ai écrites dans le cadre d’un échange avec Jean-Luc Périllié, maître de conférence en philosophie ancienne à Montpellier, et auteur de Symmetria et rationnalité harmonique, origine pythagoricienne de la notion grecque de symétrie. Ce livre, paru en 2008, montre la richesse et l’universalité de la notion pythagoricienne de symétrie, dont l’acception est plus large que la définition moderne, puisqu’elle signifie au sens propre commensurabilité, commune proportion des parties d’un tout, entre elles aussi bien qu’à l'égard de ce tout. Cette notion qui, non seulement, est intimement liée à la théorie des médiétés, mais qui peut aussi, plus profondément,  être considérée comme un arrière-plan paradigmatique, commun  aux quatre concepts fondamentaux de la mathématique pythagoricienne, et essentiel à chacun d'eux; - cette notion si importante donc, en raison pythagoricienne, n’avait, jusque là, jamais fait l'objet d'une étude systématique.

             Mais la discussion, ici, se rapporte davantage à l’objet du  travail actuel de Jean-Luc Périllié, qui est, pour citer une de ses lettres "de préciser les liens entre pythagorisme et cultes des mystères, en s'appuyant principalement sur les renseignements que l'on trouve dans une source assez ancienne et abondante : les dialogues de Platon, et dans la perspective ouverte par l’étude très forte et brillante de Peter Kingsley sur : Empédocle et la tradition pythagoricienne."*

    

  *

    

            Qu'est ce que l'oracle de Delphes? C'est la tétractys, qui est l'harmonie dans laquelle vivent les Sirènes. 

  Acousmates, Vie pythagoricienne, Jamblique. 

    

   

    

            "Penseur religieux" et "mystique" sont des prédicats que l’on voit souvent associés au nom de Pythagore. Le principal problème que je vois à leur emploi, c'est qu'ils sont presque toujours utilisés sans être définis. Or pour un chrétien, ces notions sont attachées à certaines représentations assez précises, qui n'ont pas forcément d'analogues dans le monde antique.

              En vue simplement de sortir de l'indéfinition, je propose une définition approximative. Dans le monothéisme, le mot religion désigne une relation collective et universelle à un être absent ou abscons. La mystique, elle, est la réunion d'un être exceptionnel avec la présence divine, inaccessible au commun. Ces représentations précises, dans lesquelles ces deux notions s'explicitent très bien et se complètent l'une l'autre, me paraissent décrire un modèle de religion qui ne vaut, en réalité, que pour les trois grands monothéismes,  mais qui est, finalement, assez peu pertinent pour les cultes antiques.

  *

    

              Ce n'est pas moi qui reprocherais aux historiens d'accorder de l'importance à l'aspect religieux du pythagorisme, puisque l'un des principaux griefs que j'aie contre les historiens du pythagorisme (surtout ceux opérant dans la filière de l'histoire des sciences et de la mathématique ancienne) est leur méconnaissance des faits religieux, qui s'aggrave, d'ailleurs, à mesure que ces faits sont plus anciens. Ce reproche pourrait du reste s'adresser aux intellectuels modernes dans leur généralité. Il existe des gens que l'on nous présente comme "pointus" dans leur domaine  de compétence, pour qui la religion est une espèce de disposition mentale un peu naïve, qui vous rendrait peu apte, par exemple, à l'exercice de la  science. Des notions aussi grossières de la religion, même pas dignes du niveau d'un  journal télévisé, sont aujourd’hui monnaie courante. Un autre travers du même genre, est celui qui consiste, lorsqu'on prononce les mots de  mystère  ou d'initiation, à les accompagner d'une sensation d'interdit ou de frisson, aussi ridicule que possible.

  *

    

              Commençons  par énoncer une série de propositions parfaitement triviales, qui ne sont intéressantes que par les gloses qui les accompagnent et qui en définissent aussi exactement que possible la portée.

            1. Les pythagoriciens, et Pythagore lui-même, pratiquaient des cultes religieux. C'est là un attribut qu'ils partageaient avec l'ensemble des hommes du monde antique.

            2. Les pythagoriciens, et Pythagore lui même, pratiquaient des cultes exotiques. C'est là un attribut qu'ils partageaient, au moins, avec une grande partie de la classe cultivée du monde grec, pour laquelle la religion  "commune", ou populaire, apparaissait comme trop dégradée pour permettre, à elle seule, une véritable élaboration théologique. Les anciens n'opposaient pas leur culte religieux à ceux des autres, puisqu'ils pensaient que les dieux des autres peuples n'existaient pas moins que les leurs. La comparaison des dieux d'un panthéon national, avec ceux des peuples voisins, était donc, dans le monde ancien, un simple exercice de théologie ordinaire. D'où le risque, pour le moderne qui s'attarde à ces analogies, à ces correspondances entre différents cultes, d'une véritable  hémorragie de signification religieuse, qui permet par exemple à certains, sans beaucoup d'effort, de voir dans le Pythagorisme un mélange de chamanisme hyperboréen, d'apollinisme, de dyonysisme, d'orphisme, sans exclusion de la théologie égyptienne, du mazdéisme, du zoroastrisme, du brahmanisme et bien sûr du druidisme.

            3. Quand bien même on parviendrait  à une description plus précise. Par exemple : les pythagoriciens étaient une secte orphique. Ou encore : le pythagorisme est une nouvelle formulation du chamanisme hyperboréen, on n’aurait rien obtenu de fondamentalement nouveau par rapport au niveau 1. Les initiations, les mystères, même s'ils étaient réservés à de petits groupes, ne constituaient qu'un niveau supérieur de cette dimension du religieux qui était une dimension ordinaire et normale de la vie humaine, de toute vie humaine.

              Le risque qu’il y a ici, c'est celui de chercher une correspondance entre deux plans de réalité qui n'ont, a priori, pas de rapport intrinsèque. Par exemple : Adam Smith et Ricardo sont les fondateurs de la pensée libérale. Adam Smith et Ricardo étaient de religion anglicane. Donc, le libéralisme est une secte religieuse affiliée à l'anglicanisme. L'exemple est bien sûr exagéré, cependant, il indique bien le profond sophisme qu'il peut y avoir à mettre sur le même plan un événement singulier et extraordinaire de l'histoire, tel que la naissance du libéralisme, avec des faits parfaitement ordinaires à tous les hommes d'une même époque; et le sophisme est à peu près le même dans le cas du pythagorisme, où il n'y a pas plus de raison  a priori de relier un événement aussi extraordinaire et singulier que l'apparition de la doctrine de Pythagore, ses concepts, ses réalisations scientifiques et intellectuelles, avec un plan parfaitement ordinaire  et pour ainsi dire "neutre" de la vie de son temps, qui est celui de la religion.

  *

    

          Quand bien même on réussirait à rendre aussi précise que possible une définition relevant du niveau 3. Par exemple : "les pythagoriciens étaient une secte orphique", ce serait là, j'en conviens, une information historique intéressante, mais on n'aurait toujours pas commencé à parler de la foi propre qui caractérise les pythagoriciens en tant que pythagoriciens. Or sur ce point là, il y a une pièce sur laquelle la décision est préconditionnelle : c'est le serment pythagoricien.

              Si le serment est authentique, s'il remonte au premier groupe pythagoricien, alors la foi pythagoricienne n'est autre que la foi scientifique, elle n'est autre que la foi du mathématicien en son théorème, cette "bonne" foi, qui n'implique que l'attachement à son propre signe, et qui, dans le paradoxe logique du même nom, s'oppose à la "mauvaise" foi qui est celle du menteur, - cette foi que j'ai appelée dès ma jeunesse la foi de Spinoza, et qu'il professait à ceux de ses correspondants qui lui demandaient comment il pouvait être certain de ses thèses :  je le crois comme je crois que les trois angles d'un triangle sont égaux à deux droits. En effet, dans le serment pythagoricien, on ne vous demande pas de croire en une entité absconse ou absente, mais dans une réalité qui est présentée dans l'esprit : la tétractys. Après cela, si l'on tient toujours à ce que Pythagore soit le fondateur d'une nouvelle religion, il serait tout de même honnête de préciser, à un moment ou un autre, que cette nouvelle religion s'appelle la science.

  *

    

              La décision sur le serment pythagoricien est donc préconditionnelle. Je dis bien la décision, car, est il authentique?  Le fait qu'il soit mentionné par 4 ou 5 auteurs est-il une preuve suffisante? Certainement pas. Si l’on nous dit que la lecture d'une trentaine de thèses, de préférence rédigées en allemand, peut aider à trancher la question, je ne suis pas sûr que ces arguments puissent bouleverser un épistémologue un peu cuirassé. Alors d'où pourrait provenir une preuve plus sûre? En fait, uniquement de l'archéologie, de la découverte d'une tablette où serait inscrite le serment, et qui serait datée grâce au carbone 14 de l'époque de Pythagore, où peu après. A force de confondre ses objectifs avec ceux de je ne sais quelle méthodologie (comme si les méthodes pouvaient donner des idées à ceux qui n'en ont pas) l'histoire se trouve de plus en plus réduite à attendre de l'archéologie ses possibilités d'orientation ou de décision les plus importantes.

              Pourquoi la décision sur le serment est-elle préconditionnelle?  Parce que de cette décision dépend immédiatement l'interprétation totale de la doctrine. Autrement dit, en bonne logique, dans les cas réellement décisifs : ce n'est pas "une garantie sur l'authenticité des sources" qui permet de se former "une idée sur la doctrine"; mais c'est au contraire l'idée qu'on s'est formée sur la doctrine, qui conditionne notre opinion sur l'authenticité des sources.

              L'essentiel étant, dès lors, d'avoir au départ une certaine idée des choses, je ne vois pas comment la personnalité de l'historien pourrait n'être pas, dans tous les cas, le facteur le plus décisif. Or à cet égard, il y a certaines "vocations universitaires" qui laissent un peu perplexe. Maurice Caveing, quels que soient ses mérites et l'utilité spéciale de son travail, est un idéologue positiviste comme Auguste Comte n'a sans doute jamais rêvé d'en voir naître. Il nous présente l'histoire des sciences comme une somme de petits progrès cumulatifs, modestes et laborieux. Quelle place pourrait bien trouver Pythagore dans un processus de lecture aussi écrasant? Si on lit sa thèse, qu'apprend-on du pythagorisme? On se demande surtout, en le lisant, comment l'idée a pu lui venir  de s'orienter vers l'étude de mentalités si étrangères à sa façon naturelle de penser. Et que dire de Festugière, longtemps autorité dominante en matière d'hermétisme, qui commence aujourd'hui à nous apparaître, avec le recul, et malgré sa croix, comme une incarnation presque fanatique, caricaturale, de la mentalité scientiste du début du XXe siècle.

  *

    

              Si Pythagore n’a ni écrit, ni même laissé de trace probante de sa pensée, c‘est au moins une hypothèse admissible, que ce fut de façon assumée et volontaire. Dans l’attachement à une forme exclusivement orale de la tradition, il pouvait y avoir une dimension réellement orgueilleuse : peut-être estimait-il qu’une doctrine qui ne réussirait pas à se conserver dans les cœurs, ne méritait pas qu'on s'en souvienne. Dans ce cas, ce ne serait pas par accident, mais par essence, par vocation même, que cette doctrine se refuserait à être saisie, ou cernée, par le critère ontologique de la trace, de la preuve matérielle et écrite, qui gouverne la science historique actuelle. Cela peut aussi être un début de réponse à une question que beaucoup se posent, savoir : Où se situe la coupure entre une éventuelle forme originellement pure et cohérente de la pensée pythagoricienne, et les formes lacunaires ou dégradées dont témoignent la plupart de nos sources. Etant donné, peut-être, le caractère déjà obsolète de la forme orale de transmission que Pythagore entendait maintenir, cette "écriture dans les coeurs" pourrait bien s'être avérée plus volatile qu'il le pensait; de sorte que la "décadence" pourrait avoir commencé dès l'extinction de Pythagore.

  *

    

               Il me reste à compléter ces remarques par un dernier mot concernant la notion d'ésotérisme. Cette notion ne présente pas les mêmes inconvénients que les notions de religieux et de mystique, dans la mesure justement, où l'ésotérisme est un paradigme dans lequel différents plans d'expérience ou de connaissance, du plus profane au plus sacré, (ou encore : s'étageant de la science à la spiritualité), peuvent se superposer, sans se confondre. Pour cette raison même, la notion d'ésotérisme est la seule dans laquelle pourraient légitimement (et sans risque de mélange ou de confusion) s'effectuer certaines correspondances entre le plan de la science et celui de la spiritualité. Cela explique aussi, incidemment, que je rencontre souvent moins de problèmes avec le Pythagore des ésotéristes, maçons et autres guénoniens, (bien que mon travail n'entretienne avec les leurs aucun rapport particulier), que je n'en ai, malheureusement, avec le Pythagore de certains historiens, qui à force de "suspension" et de "retrait" méthodologique, et corrélativement, à force d'amaigrissement  progressif de tout contenu intellectuel un peu précis, aurait tendance, de plus en plus,  à ressembler à je ne sais quel homme des cavernes, qui aurait découvert la multiplication par hasard en jouant avec des noix. Dans la démarche de certains historiens, il y a le rêve d’une position neutre, en quelque sorte sécurisée, qui serait une espèce de « distance parfaite » de la pensée. Mais en épistémologie, on apprend qu’il n’y a pas d’acte scientifique neutre. La suspension elle-même n’implique pas l’absence de thèse, puisqu’elle revient souvent, en pratique, à hypostasier des thèses fantômes, - des thèses qui, même lorsqu’elles ne sont pas énoncées, peuvent n’être pas moins décisionnelles et contraignantes que celles, par exemple, qui m’ont servi dans mon travail. Dans le cas de Pythagore, ces thèses fantômes peuvent être les suivantes : « Aucun des concepts hérités de la tradition pythagoricienne n’a de valeur centrale ou décisive pour l’interprétation totale de la doctrine. » Ou encore : « Si parmi les concepts hérités de la tradition, certains peuvent avoir une valeur centrale ou décisive, nous sommes incapables de dire lesquels. » Et derrière ces thèses qui ont encore un air assez précautionneux, s’en profile une autre, plus massive et en réalité seule déterminante, qui est que la doctrine de Pythagore n’a pas de consistance scientifique interne, qui en permettrait l’exposé par une méthode strictement hypothético-déductive.

    

               *Dans le même courrier, Jean-Luc Périllié précise ainsi l'angle d'attaque : "l'intuition originaire qui avait gouverné mon travail résidait moins dans la philosophie du nombre proprement dite que dans l'étude de la filiation orphisme, pythagorisme, platonisme (que je considère comme relevant d'un déploiement "dynamique" dans un sens bergsonien)."

    

  Reférences :

  Jean-Luc Périllié : Symmetria et rationalité harmonique, origine pythagoricienne de la notion grecque de symétrie, L’harmattan, 2008.

  Maurice Caveing : La figure et le nombre, Recherches sur les premières mathématiques des Grecs, Presses universitaires du Septentrion, 1997.

  P.-H. Michel : De Pythagore à Euclide, Contribution à l'histoire des mathématiques pré-euclidiennes, Les Belles Lettres, 1957.

  Arpad Szabo : L’aube des mathématiques grecques, Vrin, 2000.

  Peter Kingsley : Empédocle et la tradition pythagoricienne, Les Belles Lettres, 2010.

    

  
  votre commentaire
   
•  

  4. La divine distance

  Par zalmoxis dans le 20 Septembre 2012 à 08:38

   

   

  LA DIVINE DISTANCE

   

  par Axel SCHNEIDER

   

    

              Pour la commodité du lecteur, on a regroupé sous ce titre les six commentaires postés par Axel Schneider à la suite de l’article : Spirale de Théodore et polygone gnomonique de rang 4. Ceux qui voudraient en savoir plus sur les idées de M. Schneider, et notamment sur la nature de ce fameux ratio mesurant, selon lui, une limite indépassable de la connaissance humaine, pourront se rendre avec profit sur le site personnel de l’auteur :

  www.maformulederamanujan.org

                 D'autres précisions sur le site de "l'homme de Vitruve" :     

  http://screencircles.wordpress.com/2008/01/03/lhomme-de-vitruve/

   

   

   

  1.

  Mardi 4 Septembre

              En fait, je suis d'accord avec toi pour dire que tous les gnomons sont équivalents quand on considère les polygones réguliers. Le problème vient du cercle (ou plus exactement du disque) : ce n'est pas un polygone avec une infinité de cotés ou en tous cas pas plus qu'un polygone avec un seul côté. 

              Dès lors, oui, le gnomon est bien la notion archaïque, sauf qu'elle nous conduit à affirmer avec Gödel que épistémologie/ontologie est inférieur strictement à 1. La question est de savoir quel est ce ratio… Cela ne concerne pas seulement les mathématiques, mais toute connaissance humaine ou surhumaine. Ce ratio ne peut être dépassé que par un concept que l'on peut appeler Dieu ou Oracle (comme Turing) mais qui pour moi n'a aucune vérité en soi, à moins de considérer que la connaissance de ce ratio confère a celui qui la détient cette vérité complète.

              Nicolas de Cues était le précurseur de Gödel quant à propos de la question de la transcendance de pi (la quadrature du Cercle), il affirmait :

              "(ceux) qui ont cherché la quadrature du cercle ont présupposé la coïncidence du cercle et du carré dans l’égalité, laquelle n’est assurément pas possible au niveau sensible. Car il n’existe pas de carré qui ne soit inégal à n’importe quel cercle engagé dans la matière. Cette égalité, qu’ils ont présupposée, ils ne l’ont donc pas vue avec leurs yeux physiques, mais avec leurs yeux mentaux, et s’ils ont essayé de la démontrer par le raisonnement, ils ont cependant échoué, puisque la raison n’admet pas la coïncidence des opposés. C’est intellectuellement qu’ils auraient dû chercher la coïncidence dans ce cercle qui est égal dans chaque polygone "

              C'est la même chose que de dire que tous les gnomons sont identiques. Sauf que dès lors il faut admettre une incomplétude, une dualité du gnomon dans la mesure où le choix canonique entre la factorielle de 0,  0!=1 et 0!=-1 n'est pas symétrique au choix canonique entre i^2=-1 et i^1/2=-1. Il existe un isomorphisme entre le gnomon des réels et le gnomon des imaginaires, mais le gnomon complexe n'est pas atteignable sans une "approximation"  (le foncteur d'oubli du plan complexe considéré comme une surface de Riemann universelle).

   

   

  2.

  Mardi 4 Septembre

               Seul compte le corps des complexes, la clôture algébrique du corps des réels sur le corps des nombres imaginaires : c'est l'unique représentation possible de l'espace sensible et, comme je l'ai dit, sur cet espace sensible, le gnomon "complexe" est obligatoirement dual, c'est à dire que le gnomon "véritable" n'est pas accessible au sensible. 

               Cela se décline selon moi : avec l'inégalité isopérimétrique (rappelez vous de la création de Carthage par Didon...). Dans ce cadre, le cercle et le triangle équilatéral sont des extremums : le cercle est le "polygone" qui par rapport au "périmètre" (circonférence) a la surface la plus importante et le triangle équilatéral celui qui pour le même périmètre a la plus petite surface. Le carré est donc le premier polygone et permet de calculer le cycle d'obstruction... C'est ainsi que l'on trouve la construction de Vitruve.

              On a alors en reprenant votre logique 2 carrés gnomiques et non un seul (car alors le centre du cercle et le centre du grand carré vitruvien sont distants d'une unité). Le carré gnomon de rang 5 qui se décompose en 2 rectangles : l'un de 4 sur 1 et de diagonale racine 17 et l'autre de 4 sur 5 et de diagonale racine de 41, et le carré gnomon de rang 4 qui se décompose alors en 2 rectangles, le rectangle de 4 sur 1 (le même que précédemment) de diagonale racine de 17 et le rectangle pythagoricien (triangle isiaque) de 3 sur 4 et diagonale 5.

   

   

             La tradition compagnonique reprise par les traditions maçonniques, considère le problème ainsi : on ne peut pas mieux faire comme polygone gnomique complexe que le carré long de 3 sur 4. Donc, dans ces traditions le fameux ratio correspond à la surface du carré long divisée par la surface du carré possédant le même périmètre de 14. On trouve ainsi un ratio de 12/12,25 soit un peu plus de 97 %. L'incomplétude dans cette logique serait donc d'un peu plus de 2 % seulement... C'est très faible (et donc forcément très subversif pour les Eglises) et en même temps très important pour les positivistes car, cet univers platonicien nous est bien inaccessible (mais l'on saurait si cela est exact à quelle divine distance de nous il se trouve).

              Je ne serai pas plus long pour le moment, mais il faut bien comprendre le phénomène d'obstruction : c'est la parabole de la pêche miraculeuse partagée par Pythagore selon Jamblique et par le Christ selon Saint Jean (tiens le Christ aurait reçu un enseignement pythagoricien? Peut-être est-ce le fils d'Isis et d'Amon-Osiris comme pouvait l'être, par exemple, Césarion-Horus...) Les poissons ce sont les vesica piscis, 1/2 de la racine de 3, les mailles du filet, le polygone gnomique de rang 4 : reste toujours 153 = 1!+...+5! = 1+...+17...

   

   

  3.

  Mardi 4 Septembre

               Tout d'abord, diverses représentations du carré long de 3 sur 4 dans les traditions maçonnique et chrétienne : 

   

                 

                      

    

                 Et le double centre de la construction de Vitruve chez les Templiers :

    

   

    

  4.

  Mercredi 5 Septembre

              Votre remarque sur la conception Euclidienne, "le point est ce qui n'a pas de parties" et celle plus monadique (dans le sens de Leibniz) de Pythagore "10 points sont montrés ou présentés dans la pensée" (le Tetracktys) est particulièrement bien venue. 

              Etienne Klein, physicien spécialiste de la question du temps, a bien fixé le cadre qui a animé de vives discussions entre Stephen Hawking et Roger Penrose en 1997 sur la Relativité générale. En effet, le cadre théorique relationnel de la RG (continuum espace-temps), puisqu'il ne peut jamais être "vide" absolument : il existe toujours un tenseur métrique, un champ qui ne s'annule jamais "en tout point" du continuum. Comme les équations de Maxwell traitent du champ électromagnétique, les équations d'Einstein traitent de ce champ. Ainsi la RG, qui se veut une vraie théorie par rapport à l'approche de Newton qui retient l'espace et le temps comme des absolus (je dirais même la matière et donc la gravité), n'existe pas sans sa métrique. Or pour définir un champ, il faut définir ce champ : l'approche pythagoricienne du Tetracktys me semble tout a fait adaptée puisqu'il s’agit comme vous le dites d'un ensemble de 10 points, un champ logique. Le tenseur métrique ne s'annule en aucun point "euclidien" : en clair, pas d'annulation, pas de singularités (style trou noir) dans la RG car sinon il faut considérer la disparition de la métrique. Sauf à considérer, comme le très pythagoricien (selon moi) Aristote, que le 1 n'est pas un nombre mais une idéalité platonicienne inatteignable...

   

   

  5.

  Mercredi 5 Septembre

              Je trouve très intéressante l'idée de dire que quel que soit le polygone régulier envisagé, eh bien le gnomon est "équivalent" (à n-près) et de parler de polygone gnomique plutôt que de gnomon.

              C'est comme l'approche pythagoricienne de N. de Cues qui affirme qu'il n'existe "pas de carré qui ne soit inégal à n'importe quel cercle". Il ne dit pas que la quadrature du cercle est possible, il dit juste que comme le cercle (disque) partage avec le carré (et donc tout autre polygone régulier) les concepts de longueur (D1) (circonférence) et de surface (D2) (aire), eh bien intellectuellement ils sont "égaux" mais que cette similitude n'est pas perceptible au niveau "sensible". Je pense que dans l'esprit de N. de Cues, en tous cas dans celui de L. de Vinci et de la "petite école cusienne d'Italie" eh bien la cause de l'impossibilité d'une quadrature était acquise, bien que la démonstration ne viendra qu'au 19ème siècle. Dans l'esprit "cusien", la transcendance (le mot est anachronique) de pi n'est donc pas le signe d'une "inégalité" mais d'une obstruction, une homologie ou plus exactement une cohomologie (là encore ce sont des anachronismes), c'est à dire l'obstruction qu'ont certaines suites de morphismes (deux ensembles avec une même structure comme par exemple dans le cas d'espèce les polygones et les cercles) à être exactes.

              Ainsi le raisonnement que l'on fait sur le carré est valable à n-près pour n'importe quel polygone régulier (du triangle équilatéral au polygone avec une infinité dénombrable de cotés). 

              Attention ! Je dis bien un polygone avec une infinité dénombrable (au sens de Cantor donc avant diagonalisation vers l'infini indénombrable des Réels) de côtés. Dans mon idée, un polygone avec une infinité indénombrable de côtés, c'est un cercle.

              L'idée de rajouter l'hypothèse du continu (ou du discret) à l'ensemble des axiomes d'une théorie formelle capable de formaliser l'arithmétique et récursivement axiomatisable (logique du 2nd ordre) ne change rien au fait qu'elle contient des propositions contradictoires (consistance) ou indécidables (complétude). Il résulte en fait des travaux de Gödel de 1938 et de Paul Cohen de 1963 (avec sa célèbre méthode de Forcing) que l'hypothèse du continu est indécidable. Donc, pas plus de complémentation avec l'axiome du continu qu'avec n'importe quel axiome (comme l'axiome de protection de la chronologie de Stephen Hawking pour la relativité générale...). Ainsi, on ne sait pas si il y a des trous ou non dans la droite réelle, c'est à dire si le cardinal transfini de l'infini indénombrable des réels (aleph 1) est le successeur immédiat du cardinal transfini de l'infini dénombrable (aleph 0).

              L'idée de l'angle d'attaque est donc de dire (un peu comme l'intrication quantique) qu'au niveau "sensible" (au sens de N. de Cues), eh bien il faut considérer que les 2 sont vrais et que l'on ne peut pas calculer le cardinal aleph 1/2 soit parce qu'il n'existe pas et que la relation d'ordre entre aleph 0 et aleph 1 est "séparée" par rien ou plus exactement un objet qui n'est pas défini dans les mathématiques, soit parce que l'on ne peut connaître la position absolu de aleph 1/2, les trous dans la droite réelle n'étant alors pas calculables exactement.

              Ces deux hypothèses au niveau "sensible" sont donc identiques en dernière analyse... Mais, il y a selon moi un mais, puisqu'au niveau "sensible", on démontre en tous cas des "trous" logiques (qu'ils soient virtuels ou réels) et peut-être que l'on peut calculer l'importance de ces trous à défaut de les situer.  

              J'ai déjà montré comment Léonard de Vinci (et bien entendu Vitruve) envisageait la question : c'est l'unité isopérimétrique. On a beaucoup dit que l'homme vitruvien était la représentation des mensurations de l'homme idéal... Oui et non : la perspective de Vitruve c'est de mesurer la "divine distance", c'est à dire "si" "Dieu" a fait l'homme à son image (parfaite), dans quelle mesure l'homme (ou Dieu par récursivité...) peut-il appréhender la "pensée divine" (la vérité). Vitruve parle de cela d'ailleurs dans la partie de son "de Architectura" consacrée à la construction des temples (comme le mythe compagnonique et franc-maçon de la construction du temple de Salomon : l'équerre et le compas avec la question du centre de gravité G). Vitruve (et le Vinci) veulent mesurer ainsi le rapport entre l'ontologie (la sémantique) et l'épistémologie (la syntaxe), la "divine distance".

              Voilà l'idée de Vitruve... et celle d'Emil Post : mesurer le RE Turing degree universel, que l'on peut formuler selon moi ainsi : "Quel est le plus petit x qui permet d'avoir une théorie capable de formaliser l'arithmétique (structure algébrique ternaire), récursivement axiomatisable à 100x %, consistante et complète au sens de Gödel ?"

   

   

    

            Le centre du cercle, et celui du carré : dans la construction de Vitruve on retrouve l'"égalité" de N. de Cues c'est à dire que le rapport entre le côté du carré et le rayon du cercle quand on les met dans une relation triangulaire (puisqu’on ne peut distinguer entre les 2 extremums du triangle équilatéral - minimun isopérimétrique dénombrable - et le cercle maximum isopérimétrique indénombrable) est de 8/5 unités, l'unité étant la "distance" entre le centre du cercle et celui du carré (la métrique qui ne s'annule en aucun point de l'espace-temps relativiste...)

              Bon et quid du Gnomon ?

              Le Gnomon c'est 2n+1. Mais, pour les nombres imaginaires ? 2n-1.

              Maintenant, sur le plan complexe ? Et bien, c'est là où l'unité du Tretracktys : le Tretracktys en tant que théorie formelle ne peut servir à axiomatiser complètement la "théorie formelle" (méta-modèle) et donc conceptualiser complètement le gnomon complexe.

              L'unité gnomique de référence est donc le gnomon de rang 4, le gnomon quadratique. On ne peut aller en dessous. Ainsi on a une rupture de symétrie entre la plus petite chaine de Cunningham (chaîne de nombres premiers) de type 1 (2n+1) et de poids 5 (4 itérations) : 2, 5, 11, 23, 47 et  la plus petite du type 2 (2n-1) et de même poids qui commence par 1531 :

              1531 3061 6121 12241 24481

              Pourquoi ce 1531 : car 1!+...+5! = 1+...+17 = 153

              Rappelons que la somme infinie de l'inverse des factorielles nous donne le nombre e, base des logarithmes népériens. Mais contrairement à ce que pourrait laisser penser l'identité d'Euler eî.pi = -1 (donc Dieu existe disait Euler à Diderot à la Cour de la Grande Catherine...) : la transcendance de e et de pi ne sont pas forcément équivalentes dans le sens où l'on peut avoir des nombres transcendants comme e avec une mesure d'irrationalité  égale à 2 comme pour les irrationnels algébriques (par exemple les racines des nombres premiers). On ne connait pas la mesure d'irrationalité de pi (enfin moi je crois que si : on prend juste mon ratio et 2+2*2,08 %).

              Ainsi, si effectivement les log naturels permettent de faire d'une multiplication une addition, on peut montrer la convergence vers pi de la moyenne arithmético-géométrique (AGM) de 1 et 1/racine de 2 (cf. la formule de Brent-Salmin).

   

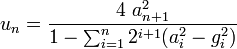
              Sauf que la vitesse de convergence de la somme des inverses des factorielles vers e est peut-être plus rapide que la convergence de la moyenne AGM de 1 et de 1/racine de 2 vers pi.

              (la suite prochainement)

   

   

  6.

  Vendredi 14 Septembre

              La recherche des bonnes proportions entre le diamètre des colonnes des temples et leur hauteur a conduit dans la Grèce antique aux différents ordres architecturaux (on en recense 5 traditionnellement mais les plus importants sont les ordres dorique, ionique et composites). La question qui se posait était bien évidemment la quadrature du cercle.

              L'ordre Dorique semble privilégier le carré "vitruvien" plutôt que le cercle "vitruvien" : 8 plutôt que 10. A l'inverse, l’ionique privilégie plutôt le 10 par rapport au 8. Les ordres composites "tâtonnent" entre ces 2 extrêmes. Vitruve nous montre que la divine proportion n'est atteignable que de façon approximative (le carré long).

    

    

   

   

  
  votre commentaire
   
•  

  1. Le développement continu de la tétractys

  Par zalmoxis dans le 12 Septembre 2012 à 12:05

  
  
  
    

     

  LE DEVELOPPEMENT CONTINU

   DE LA TETRACTYS

    

    

  par Guillaume DENOM

   

   

   

  Et, par dessus tout,

  respecte toi toi-même.

  Vers d'or de Pythagore

    

   

   

    

   

   

   I.    LA LOI DU GNOMON

    

  "L'ensemble des gnomons du carré, est égal à l'ensemble des gnomons du triangle équilatéral, est égal à l'ensemble des nombres entiers Impairs."

   

   

  La loi du gnomon : G(c) = G(t.e) = I,  exposée, sur ce blog, dans les trois premiers articles de la deuxième section, est une loi importante de la mathématique.* S’il peut paraître étonnant qu'elle ne soit pas reconnue comme telle, et plus encore, qu'elle semble même inconnue de la littérature mathématique contemporaine, il y a en réalité à cela des raisons précises et pour ainsi dire naturelles.

  La loi du gnomon est une loi synthétique, dont les applications se répartissent à égalité entre trois domaines de la mathématique : arithmétique, géométrie, logique. Pourtant, ce n’est pas une loi générale, c'est-à-dire qu’elle ne surplombe pas ces différents domaines à partir d’une position extérieure et dominante, mais, bien au contraire, elle agit à l’intérieur de chacun d’eux d’une manière spécifique.

  La mathématique moderne n’est pas synthétique. Son geste le plus caractéristique est la généralisation, - geste qui est précisément à l'opposé de la synthèse, puisqu’il consiste, à partir d’un cas particulier, à définir une extension de ce cas particulier à tout un domaine d’objets apparentés, par une action qui se qualifie elle-même de « conventionnelle ». Par exemple : « tous les entiers peuvent être considérés comme des nombres décimaux ». Ou encore : « les entiers peuvent être considérés comme des fractions. »  La généralisation, lorsqu'elle est pratiquée, comme elle l'est dans la mathématique moderne, de façon machinale, entraîne une double tendance de l'esprit mathématique, d'une part, à considérer comme "premier" l'objet qui est le plus tard venu, ou le plus récemment défini, (tel que le nombre réel ou le nombre imaginaire), d'autre part, à considérer qu'il n’existe pas de naturalité mathématique, mais que la mathématique est une façon de définir les choses qui est "conventionnelle" par essence, qui peut être "librement choisie".**

    

  Commençons par détailler les trois premiers domaines d’application de la loi du gnomon.

   

  1.      En arithmétique, la structure du gnomon est la triple articulation, intégralement coordonnée, du nombre impair (gnomon), du nombre entier ordinal (côté du polygone), et du nombre carré  (polygone gnomonique). 

    

    

   

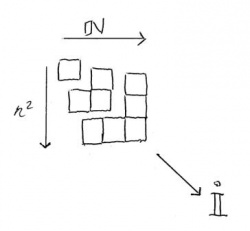
                 Dans cette structure, on a, sur l’axe horizontal ; la série infinie des nombres entiers ordinaux (1, 2, 3, 4, ...) ; sur la diagonale, la série des impairs (1, 3, 5, 7, ...) ; enfin, sur l’axe des résolutions, la série des nombres carrés : (1, 4, 9, 16,...)

   

              Cette particularité apparente  la structure du gnomon à d'autres structures arithmétiques connues, dont on peut prendre pour exemple la célèbre formule de Ramanujan associant les nombres pi et e, dans laquelle on retrouve, sur l'axe horizontal, la série des impairs; sur l'axe vertical, la série des entiers; et du côté de la résolution, la racine carrée, opération duale de l'opération "carré". 

   

                                                                                                  Côté résolution :

   la racine carrée

   

   

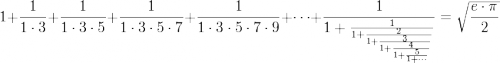
   Axe horizontal : série des impairs (1, 3, 5, 7, …)       Axe vertical : série des entiers : (1, 2, 3, 4, ...)

   

   

  2.     En géométrie, le polygone gnomonique de rang 2, triangle ou carré, est la formulation minimale (ce qui implique : quantifiée) du principe géométrique qui est recouvert par les notions modernes d’endomorphisme et d’autosimilarité; et qui est, en langage courant, la propriété d'un objet, d'être constitué de parties semblables au tout qu'elles composent. 

   

  

  polygones gnomoniques de rang 2

   

  3.      La théorie du gnomon est la plus fondamentale des théories mathématiques contenant une application biunivoque des notions de nombre entier et de figure entière, et pour cette raison elle est l'interface la plus étroite qui puisse exister entre arithmétique et géométrie. Le gnomon est un objet mathématique dans lequel arithméticité et géométricité sont coproduits : car le gnomon est un nombre; le gnomon est le nombre de figures, que l'on doit ajouter à une figure, pour la reconstituer. En tant qu’interface la plus étroite possible entre nombre et figure, entre arithmétique et géométrie, le polygone gnomonique de rang 2, triangle ou carré, est le plus petit espace logique qui puisse exister : en précisant là encore, que l’on parle d’un espace quantifié, permettant une construction quantifiée de la logique, telle que la logique des tables de vérité.

   

  4.      C’est seulement dans un quatrième temps, après avoir détaillé la liste de ses applications dans chacun des domaines de la mathématique, que la loi du gnomon peut être envisagée synthétiquement, et que peut être évaluée sa place particulière dans l’appareil de la mathématique pythagoricienne.  La théorie du gnomon permet de donner un sens précis à la notion de tétractys : "clôture à quatre", ou si l’on préfère, "clôture quaternaire"; cette clotûre correspondant à la quantité d'espace nécessaire et suffisante pour que puisse se déployer la structure du gnomon, dans laquelle : graine + gnomon = 4. Sous cette armature logique, la notion de tétractys devient une notion mathématique utilisable, rendant possible une véritable mise en ordre des concepts mathématiques pythagoriciens. 

      

        La notion de clôture est indispensable, en réalité, pour comprendre l'unité synthétique de ces différents concepts, et par suite, pour exposer de façon rigoureuse les applications contenues dans les articles 1, 2 et 3 de la première section, à savoir : tétractys = base arithmétique (inclues dimensions décimale et négative) ;  tétractys = dimensions de l’espace et objets premiers de la géométrie ; tétractys = accords musicaux = noyau du système des médiétés, (en deux applications).

    

  Par hypothèse, un traité, ou une théorie, de mathématique pythagoricienne, est un traité, ou une théorie, dont tous les axiomes sont déduits des propriétés mathématiques de la tétractys.

    

  La mathématique pythagoricienne n'a a priori besoin d'aucune autre notion mathématique que celles qu'elle produit elle-même. Dans l'absolu, même les signes utilisés devraient être justifiés par la tétractys. Les chiffres arabes pourraient êtres remplacés par des tétractys à points triangulaires, les opérations logiques par les logons binaires, etc. En pratique, c'est évidemment difficile et un peu contre-productif, mais dans la visée qui est la sienne, la mathématique pythagoricienne n'utilise pas de signes « conventionnels », mais produit les signes dont elle a besoin.

  Ceci n'est qu'un horizon, mais qui peut servir de guide. 

  Au départ, la tétractys est une idée qui n'est pas définie, mais qui est montrée, qui est présentée dans la pensée. La mathématique pythagoricienne ne fait que répéter indéfiniment ce geste premier, ou plutôt le prolonger, le poursuivre par un développement continu. 

   La mathématique pythagoricienne est le développement continu d'une structure constante qui est la tétractys, dont la fonction est de déplier successivement, application par application, toutes les parties de la mathématique. Dans l’idéal, toutes les applications de la tétractys peuvent s'enchaîner par un mouvement continu, entièrement coordonné, au moyen d'un seul et unique opérateur topologique qui est le retroussement d'une structure : mouvement par lequel le dessous passe au dessus, et le dedans au dehors, par une poussée continuelle, et qui est en relation avec des objets topologiques tels que le ruban ou la bouteille de Moebius. La question est complexe, mais dans l'idéal la présentation écrite de la mathématique pythagoricienne n'est pas la forme préférable. Une animation en 3D avec une voix off serait plus parlante, parce qu’elle permettrait d'avoir, au lieu d'images arrêtées, un mouvement réellement continu où l'on ne perdrait jamais de vue la structure ponctiforme à 10 points produite au départ.***

    

  *Son ancienneté, sous cette forme, est attestée notamment par Jean Philopon qui, dans son commentaire de la physique d'Aristote, affirme que les anciens appelaient gnomons les nombres impairs.
  

  **Le problème de la mathématique moderne n'est donc pas de généraliser, mais d'ignorer qu'à chaque fois qu'elle généralise, elle sacrifie de l'ontologie, de l'être, au profit de la seule puissance du signe. 

  ***S'il y a unité de la science, alors cette unité doit consister dans une pensée. Il s'agit là, en somme, d'une simple réquisition logique de la science, bien que la science occidentale moderne semble l'avoir totalement perdue de vue.

    

        

    

       

  II.     LA CONSTRUCTION PYTHAGORICIENNE DE LA GEOMETRIE.

    

  En dehors de la théorie du gnomon, l'un des aspects les plus importants de la mathématique pythagoricienne réside dans la façon de définir les dimensions et les objets premiers de la géométrie, par une méthode qui est foncièrement différente de celle d'Euclide, en ce qu'elle consiste à associer de façon rigoureuse, à chacune des dimensions ou des objets qu'elle définit, la quantification des opérations de pensée correspondantes à ces objets, comme à ces dimensions. Le référent absolu n'est autre que le temps, mais pas n'importe quel temps, le temps des opérations mathématiques; ici, l'opération : poser un nouveau point.

    

  

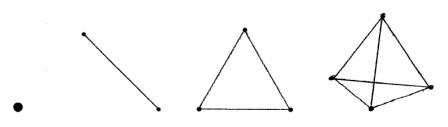
                                     1                  2                   3                  4

   

  Il est possible d'illustrer cela dans un cadre épistémologique moderne et rigoureux, tel que, par exemple, la théorie de la forme logique de Granger. Dans le système de Granger, la relation à partir de laquelle est défini tout contenu de science mathématique, est la liaison entre une opération de pensée, (pour nous : un mouvement de la tétractys, une application), et un objet de pensée, (l'objet mathématique qui est défini à chaque nouvelle application.) C'est exactement le sens qu'il faut attribuer à la sentence classique : Une figure, un pas. A chaque objet défini, correspond une opération de pensée qui est quantifiée et engrammée de façon rigoureuse. Ainsi, dans la construction des objets géométriques, les 4 objets premiers sont d'abord construits synthétiquement, comme ci-dessus, en utilisant les dix points de la tétractys, puis analytiquement - construction à 24 unités-points -, au moyen cette fois des factorielles des quatre premiers nombres.

    

  

                                1x1          2x1            3x2x1                4x3x2x1

    

  Granger appelle dualité la corrélation, qui est en fait une relation de cogenèse, de coengendrement, entre une opération mathématique, et un objet mathématique; et il suggère que le modèle premier de cette relation est à rechercher dans la dualité des opérations arithmétiques, - dualité conçue, semble-t-il, comme une interrelation généralisée, et de nature organique, entre toutes les opérations primitives sur le nombre entier, à l'image de la dualité des solides réguliers illustrée au chapitre suivant, dont on peut penser qu'elle constitue, elle aussi, un cas fondamental. D'où l'importance de définir de façon systématique ces fameuses relations de dualité, telles que :

   ST = D(PG)  

  Où  ST : spirale de Théodore; PG : polygone gnomonique; D : Dualité, définie comme une application biunivoque sur l'ensemble des entiers.   

          

  Cependant, il n'y a, semble-t-il, que dans la mathématique pythagoricienne que l'exigence du programme de Granger s'avère pleinement applicable.

   Pour le comprendre, il faut se poser la question de ce qu’est l’acte premier, l’acte fondateur de la mathématique.

  Comparons le début d’Euclide avec le début de Pythagore.

  Euclide : "Le point est ce qui n'a pas de partie".

  
  On veut déjà donner une définition logique. On veut définir l'élément premier à partir d'un lieu de la science qui est ultérieur à lui, puisque c'est lui, le point, qui doit permettre de construire tout le reste. On est déjà dans la conception des modernes, où tout doit être produit à partir de ce qui vient en dernier : la logique.

  Début de Pythagore : Dix points sont présentés dans la pensée. Pythagore est conscient que l'atome, l'élément premier de la mathématique, ne peut être défini par rien de plus originaire que lui-même, sans tomber dans d'insolubles paradoxes,  mais qu’il peut seulement être produit, montré, ou présenté dans la pensée. Encore n'est-ce possible qu'en l'articulant sous la forme d’une structure, d’un champ. Ce n'est que de la considération  des relations existant entre ces points, telles que symétries ou homothéties, qu'une définition plus précise de l'élément, ou de l'objet premier pourra se dégager; et celui-ci reçoit alors un statut bivalent, à la fois arithmétique et géométrique, qui est celui d'"unité-point", ou "unité ayant position".

  
  De cette manière, on évite, comme Euclide, de construire la mathématique à partir d'une définition qui n'a pas de sens mathématique. La force de la mathématique pythagoricienne consiste toute entière dans cette sagesse, dans cette « prudence » du commencement. Mais aussi dans l'usage congru de cette action constituante qu'est la définition d'un objet mathématique, à partir des opérations de pensée qui l'engendrent. Une figure (un objet), Un pas (une opération) : et l’on quantifie.

  Celui qui énonce : "Zéro est le nom de l'ensemble qui ne contient pas d'ensemble", ne fait que répéter la proposition : "Le point est ce qui n'a pas de partie." Le geste qu'il répète est une erreur, qui consiste à penser que la mathématique est une phrase, que son être consiste dans une phrase, et que donc on peut le présenter dans une phrase. L'être de la mathématique ne peut pas consister dans une phrase, parce que la mathématique ne devient une phrase qu'à partir d'un certain moment, qu’on qualifiera volontiers de moment opportun. Et il est impossible de dégager, de définir correctement ce moment opportun, si l'on n’a pas compté tous les mouvements qui ont été accomplis auparavant.

  Si l’on compte  à l’envers, - la manie des modernes, - ou si l'on essaie d'engendrer les premières opérations à partir des dernières, on échouera  à chaque fois; et l’on parviendra toujours à des conclusions du genre : "Ce sont les irrationnels qui engendrent les rationnels".

  Voilà, en bref, les raisons qui peuvent expliquer que le moment logique, - le gnomon - soit resté jusqu’ici inaccessible à l’intelligence des modernes.

    

    

    

    

  III. DUALITE MATHEMATIQUE ET SYNTHESE A PRIORI

    

  La notion de dualité constitue pour Granger une catégorie philosophique, dont l'acception est dérivée des définitions mathématiques de ce terme, elles-mêmes variées, sans se confondre avec l'une d'entre elles en particulier. Citons l'une des définitions données par Granger de cette notion, - définitions qui, pour être non seulement diverses, mais souvent, comme ici, prudentes et programmatiques, ne doivent pas masquer le caractère urgent et impérieux qu'elles revêtent, sans nul doute, pour leur auteur.

  "Au sens où nous l'entendons, la notion de dualité comme catégorie philosophique conduirait à formuler le principe de la nécessité d'une détermination réciproque de tout système d'objets de pensée et d'un système d'opérations intellectuelles associé."

  A cette définition liminaire, il faut ajouter cette précision tout aussi essentielle, que, dans le développement de la mathématique, ce qui était objet d'un certain point de vue antérieur, peut, à son tour, devenir opérateur d'un point de vue nouvellement formulé, - la dualité devenant ainsi le vecteur, non seulement de la continuité du raisonnement ou du discours mathématique, mais de la constance d'une certaine forme logique.

  La dualité grangérienne a vocation à se substituer à la notion kantienne de "synthétique a priori", dont elle reprend toutefois les réquisitions. Un système opérations-objets dual et consistant peut être considéré comme un "ensemble" synthétique a priori de vérités mathématiques.  Mais la notion  de dualité est aussi intimement liée à celle de nature mathématique, et à la définition de ce que peut être un objet mathématique naturel, dans la mesure où elle tend à associer la définition des objets mathématiques, autant à des lois physico-chimiques de la nature, qu'à des actions concrètes de l'homme, qu'elles soient d'ordre psychique ou physique, - sans exclusion du musculaire -, d'un caractère assez universel, idée qu'avait déjà thématisée, en son temps, la théorie de la forme, ou même la pensée formelle en général. 

  Concernant cette catégorie, ce que l'on peut remarquer d'abord est son caractère moniste, d'une part, parce qu'elle ne s'inscrit pas dans un ensemble de catégories de même niveau, mais se présente comme un véritable singleton catégoriel, d'autre part, parce que la dualité elle-même est réellement une, même si elle contient le deux, en ce qu'elle s'exprime, comme on l'a dit, par le maintien ou la constance, d'application en application, d'une certaine forme logique; en quoi elle se veut précisément synthèse; et par où se justifie aussi sa prétention singulière à être apparemment, pour Granger, la catégorie ultime de la science

  Dans un cadre différent, qui est celui - métaphysique - de la définition du symbolisme et de la pensée symbolique, René Guénon a, lui aussi, donné de brillantes définitions de la synthèse et du synthétique, qui ont plusieurs traits congruents avec celle esquissée ici. 

    

  Dualité des solides réguliers 

   

  Polyèdres inscrits : tétraèdre                     octaèdre                         icosaèdre 

            

  Polyèdres circonscrits : tétraèdre                  cube                            dodécaèdre

   

  Le tétraèdre, à gauche, est le dual de lui-même. Dans cette relation généralisée, l'ensemble des relations de dualité entre solides réguliers considérés par paires, est déductible, ou dérivable, du développement gnomonique tridimensionnel d'une seule et unique structure géométrique : le triangle équilatéral. En effet, les trois polyèdres primitifs - ici en couleurs et inscrits, dont ceux en arrêtes rouges et circonscrits (dans la succession desquels on retrouve les valeurs 3 - 4 - 5 du triangle isiaque) sont les duaux; - ces trois polyèdres inscrits peuvent être construits au moyen de triangles gnomoniques de rang 2 : 1 pour le tétraèdre, 2 pour l'octaèdre, 5 pour l'icosaèdre. Autrement dit : les polyèdres réguliers sont contenus de manière synthétique a priori dans les seules propriétés intrinsèques de développement gnomonique, d'une part, et de clôture géométrique tridimensionnelle, d'autre part, qui sont celles du triangle équilatéral. Ou encore, le triangle gnomonique de rang 2 est la constante logique du système opérations-objets dans lequel consiste et se déploie ici la nature, la définition même des polyèdres réguliers.

  tétraèdre + octaèdre + icosaèdre = (1 + 2 + 5) x triangle gnomonique de rang 2

  

  Quant à la série des polyèdres rouges : tétraèdre, cube, dodécaèdre, elle s'obtient par la transformation des premiers polyèdres, d'objets qu'ils étaient, en opérateurs, les sommets de ces polyèdres devenant les centres de référence des faces des polyèdres circonscrits, mathématiquement suffisants à les définir. A leur tour, ces polyèdres rouges peuvent devenir les opérateurs de la construction des trois premiers, par une transformation duale de la précédente.

     

   

   

   

   

  IV. MATHEMATIQUE MODERNE / MATHEMATIQUE PYTHAGORICIENNE

   

   

  Il y aurait d'autres sujets à évoquer, concernant les différences de style entre mathématique pythagoricienne et mathématique moderne. L'exercice peut paraître scabreux, dans la mesure où il est entendu qu'il est impossible de parler de "style" mathématique, sans recourir, ça et là, à des images physiques. Ces images ne sont donc pas à prendre au pied de la lettre, mais un peu en retrait, comme des métaphores ici assumées.

  La mathématique moderne semble considérer comme réel, - et même comme unique réel - le "substrat" ou le "fond" indéfini de l'espace intelligible, - quel que soit le nombre de dimensions qu'elle veuille lui prêter -, indépendamment des objets que l'on peut définir à l'intérieur de lui. Cet espace a l'apparence d'un "donné" objectif, déjà développé, au sein duquel règnent, en tout point, l'"isotropie" ou l'équivalence ontologique, et  la symétrie, au sens moderne et saturé d'indifférenciation*. Enfin, cet espace est conçu comme indépendant de la situation native, ou naturelle, de l'homme. L'espace pythagoricien est, au contraire, un espace précisément dual, où la définition du "fond" indéfini est inséparable de celle d'objets définis, et où règnent, de ce fait, la différence, la singularité et la polarisation en tout point. La géométrie pythagoricienne, y compris la plus fondamentale, intègre de plein droit les notions naturelles de l'orientation et de la chiralité. Mais plus important encore, l'espace pythagoricien est un espace qui a une histoire, un développement; c'est un espace dont la structure profonde est chronogénétique, faite de temps et de nombre, et où règne de ce fait aussi la différence en tout point du temps. Ces remarques, toutefois, appelleraient quelques développements complémentaires.

  *La définition moderne de la symétrie, synonyme d'uniformité ou d'indifférenciation absolue, est une extension mathématique correcte, légitime, de la définition "traditionnelle", ou pythagoricienne, synonyme de commune mesure, de commensurabilité, ou plus simplement encore, de proportion. Entre les deux, il n'y a pas de réelle rupture. La moderne n'est qu'une amplification de l'ancienne, obtenue par saturation, ou maximisation de son concept,  - amplification qui découle assez naturellement de la généralisation mathématique de la notion de symétrie, telle qu'elle se précise, en particulier, dans la théorie des groupes de Galois. Cependant, dans la nouvelle définition, le référent ultime du concept de symétrie n'est plus la symétrie d'objets, mais celle de l'espace. La saturation du concept joue donc bien ici le rôle d'épurateur, ou de liquidateur de contenu ou de déterminité ontologique, consentie au bénéfice de la seule puissance du signe, qui est caractéristique des généralisations de la mathématique moderne. Le tort de la science moderne n'étant pas - au risque de nous répéter - de pratiquer ces généralisations, mais plutôt, en vertu d'une politique de la table rase intellectuelle, de considérer systématiquement comme plus essentiel cet aspect final de la vie du concept, qui est celui de son détachement et de sa transformation en signe-outil, au mépris du chemin entier de la pensée qui a produit ce signe et l'a conduit, par des mouvements comptés, jusqu'à cet état, ou cette phase particulière de son développement.

    

    

   

   

   

  V. LA DYADE INDETERMINEE ET SES DIFFERENTS ASPECTS

                   

  La dualité Objet/Opération revêt, dans l'idée de Granger, la fonction d'"archè", ou de principe irréductible, correspondant à "ce qui reste, une fois qu'on a tout enlevé", une fois qu'on a fait abstraction, ou soustraction, de toutes les opérations et tous les objets particuliers. Cette notion n'est donc pas elle-même d'ordre mathématique, mais métamathématique.

  La tradition pythagoricienne connaît une notion analogue, que la modernité traduit habituellement, en français, par l'expression : "dyade indéfinie", mais qu'on choisit ici de nommer "dyade indéterminée", pour éviter de la confondre avec une notion de niveau inférieur. Cette notion a, en effet, dès l'antiquité, et plus gravement encore de nos jours, donné lieu à diverses méprises, du fait que chacun des termes qui la composent peut être interprété dans un sens moins universel que celui, métamathématique, et d'ordre vraiment primordial, qui est le sien en réalité. Ainsi, le terme "indéterminé" peut être confondu avec une notion de niveau inférieur, qui est le second terme, négatif, d'un cas précisément déterminé de la "dyade indéterminée" : la dyade "Défini - Indéfini". De même le terme "dyade" a pu, dans cette même expression, être compris à tort comme désignant "l'idée du Deux", c'est-à-dire comme un opérateur intervenant dans la construction de l'arithmétique, ce qu'il ne signifie en aucune manière dans cette expression, où sa portée est plus universelle, puisqu'antérieure à la définition même du nombre, comme de l'arithmétique. Dans les deux cas, l'erreur provient, comme on le voit, de la confusion du mathématique et du métamathématique.

  La langue française s'est, à l'époque moderne, trouvée pareillement embarrassée, pour donner un nom à un "représentant" historique particulier de cette dyade, objet d'un fragment inestimable de Philolaos, devenu canonique faute de source plus haute. Trois solutions ont été adoptées. Fini - Infini, Limite (ou "Limitant") - Illimité, Défini - Indéfini. Tous ces termes ont reçu, en mathématique moderne, des définitions précises, entre lesquelles existe un écart de signification important. Néanmoins, seule la première de ces traductions, qui était celle en usage au XIXe siècle, peut être considérée comme impossible, la notion de l'infini ne pouvant relever, en pythagorisme comme dans toute doctrine au sein de laquelle on se refuse à mélanger les genres, que du domaine exclusif de la connaissance métaphysique, et n'ayant pas sa place en mathématique; n'en déplaise à l'habitude hyperbolique contractée par les modernes, - habitude qui n'a pas de justification plus profonde, que le fait que la véritable notion de l'infini leur soit, en règle générale, inconnue, ou étrangère, aussi bien que toute autre notion de métaphysique véritable*.

  A ce premier noyau d'idées mathématiques, on peut d'abord relier la dyade logique du  Même et de l'Autre du Timée de Platon (Identité - Différence), dans la mesure où la partie centrale du Timée peut, selon toute vraisemblance, être considérée comme un ouvrage de l'école de Philolaos-Timée, dont Platon n'est que l'éditeur. On peut, de même, remarquer que la dualité du Discret et du Continu, bien qu'elle coure le risque de se voir taxer d'anachronisme**, constitue, pour le sens, qui seul importe ici, une traduction également légitime, et peut-être la plus éclairante, de la dyade de Philolaos. Enfin, à toutes ces dyades, on peut encore associer une variété de notions qui se rapportent, elles, à la polarisation caractéristique de la structure géométrique du gnomon; ainsi, le gnomon présente un côté Fermé et un côté Ouvert; un côté qui est l'Origine, ou l'Ombilic, et un côté auquel sont liées les idées de Croissance ou d'Augmentation.

  Dans toutes ces situations, le terme "dyade indéterminée" se rapporte donc à la paire d'universaux irréductibles qui reste au fond de la pensée mathématique, une fois qu'on l'a délestée de ce qu'elle contenait. Plus précisément, la doctrine pythagoricienne suppose que, par delà la variété d'aspects sous lesquels cette dyade se présente, il existe une forme ou un moule absolument universel, absolument vide et inconditionné, qui, comme tout ce qui est vraiment premier dans l'ordre intellectuel, demeure en lui-même insaisissable. L'essentiel demeurant toutefois que, si l'on s'attache avec sincérité à l'un de ses aspects, on est contraint, par un chemin ou un autre, de récupérer les autres.

  La dualité grangérienne Objet/Opération peut donc apparaître comme un aspect particulier de la dyade indéterminée, adéquat à un certain moment de la pensée, ou de la réalisation mathématique particulière qui est celle de la mathématique moderne, sans qu'on doive estimer pour cela qu'elle l'emporte sur les autres de manière absolue ou catégorique, en terme de primordialité, ou de fondamentalité.*** On peut d'ailleurs remarquer que, chez Granger lui-même, la dyade Forme - Contenu apparaît plusieurs fois comme une dyade concurrente et complémentaire de la dyade Opération - Objet.
  

  Les différents aspects de la dyade indéterminée ne sauraient donc donner lieu à une "table des catégories" prétendant à la complétude; et la fameuse "table des opposés" transmise par la tradition pythagoricienne sous le nom d'Alcméon de Crotone****, ne fait, à cet égard, pas plus autorité que celle que nous proposons ici, en guise de récapitulation de ce chapitre. Les notions qui suivent n'ont été choisies que parce qu'elles nous paraissent avoir un sens bien établi dans un contexte déterminé, qui est, pour nous, celui de la mathématique moderne et de son expression métamathématique. Les aspects de la dyade indéterminée sont par définition "indéterminés" dans leur nombre même, parce qu'ils relèvent de la nature, de la déterminité même de l'homme, déterminité qui est d'ordre spatio-temporel, historico-géographique, mais aussi, s'agissant d'une table de ce genre, linguistique. La doctrine pythagoricienne est, du reste, la seule que nous connaissions à formuler dans les termes les plus clairs ce principe de la contingence, notamment linguistique, du commencement de la science - au contraire de la science moderne qui s'imagine toujours pouvoir disposer d'un fondement ou même d'un objet absolu.

  "Le plus sage est le Nombre, et après lui vient celui qui donne leur nom aux choses", énonce un acousmate pythagoricien. Le nombre n'est principe de connaissance, que pour autant qu'il s'applique originairement à quelque chose d'autre; quelque chose qui n'est pas de la nature du nombre, mais qui est de la nature "exemplaire" et "permutante" (ou encore : paradigmatique), des choses nommées, des choses qui reçoivent de l'homme leur nom.

  Même la tétractys n'a pas, en pythagorisme,  le statut de commencement absolu, mais seulement celui de commencement excellent. Cette contingence du commencement n'implique, bien évidemment, aucune espèce de "relativisme" concernant la connaissance qui en est le résultat. Ce qui distingue les pythagoriciens des autres philosophes ou scientifiques, réside, principalement, dans la possession d'une certitude inébranlable, certitude qui n'est autre que la foi scientifique, et qui est par nature incommunicable, puisqu'elle ne consiste qu'en la pure intellection de ce que l'on a dans la pensée.

    

  Limite - Illimité

  Défini - Indéfini

  Discret - Continu

  Nombre - Figure

  Identité - Différence

  Objet - Opération

  Contenu - Forme

  Graine - Gnomon

  Fermé - Ouvert

  Origine - Croissance

  Cardinalité - Ordinalité

  Un - Multiple

  Minimum - Maximum

  Impair - Pair

   

    

    Parmi les représentations symboliques les plus éloquentes de la dyade indéterminée figurent, outre le prétendu symbole du soleil, qui est plus originairement celui du centre du monde, de l'ombilic, ou du pôle, le cône, ainsi que diverses adaptations prosaïques de cet objet, telles que l'entonnoir ou le sablier, ou encore, tout naturellement, les lettres V et Y de notre alphabet, ou l'accent circonflexe français ^.  

        

             

   

   

  On peut conclure en remarquant qu'en raison de sa "viduité" et de son extrême universalité, la dyade indéterminée recèle la capacité de se comprendre elle-même de façon autologique, en tant que cas particulier, sans entraîner de paradoxe manifeste, de sorte qu'on peut sans doute admettre comme cas extrême de la dyade indéterminée le couple "monade-dyade". Cette capacité autologique est une des raisons qui expliquent les confusions, dont certaines sont anciennes, qu'a suscitées cette doctrine; comme le fait qu'on ait cherché à voir dans la dyade un opérateur exclusivement arithmétique, alors qu'elle ne l'est que secondairement, en tant que le nombre naturel est un cas particulier d'ordinalité, tandis que le domaine complet dans lequel agit la notion d'ordinalité, est quant à lui, d'un degré plus profond et plus universel à la mathématique, et tel qu'on ne peut le qualifier que de métamathématique, puisqu'il est antérieur au nombre lui-même.
  

   

   

  *Généralité dont il faut exclure, aujourd'hui, certains mathématiciens éminents oeuvrant, en particulier, dans la patrie d'élection du pythagorisme, l'Italie, tels que MM. Zellini et Barazzetti.

  **Sauf par quelques mathématiciens avisés. "Le problème du continu, qui mériterait le nom de problème de Pythagore..." Hermann Weyl, Le continu et autres écrits, Vrin, 1994.

  ***Ce point reste pour nous un sujet de doute. D'un côté, la dualité opération-objet peut nous apparaître comme la plus fondamentale, comme la toute première des "émanations" de la dyade indéterminée qui, à ce titre même, demeurerait encore réellement "indéterminée" au sens de non-polarisée - de l'autre, cette primauté peut très logiquement n'être qu'une illusion, due au fait qu'elle serait adéquate au développement de certaines possibilités de la mathématique, avec lesquelles, d'aventure, les nôtres se confondraient en totalité.

  ****Ce qui se montre avec évidence dans cette image ancienne de la doctrine, c'est que la dyade indéterminée a beaucoup moins de rapport avec le nombre deux qu'avec le principe universel de l'ordinalité, en tant qu'il s'oppose à la cardinalité de la monade. L'appellation "table des opposés" semble  donc fâcheusement insuffisante, en ce qu'elle omet de préciser que ces opposés prétendent, dans la table d'Alcméon comme dans celle ci-dessus, se présenter d'une façon qui est toujours la même, selon une loi d'orientation ou de polarisation constante, ou encore, comme une suite ordonnée dans laquelle chaque terme se voit attribuer un nombre d'ordre : 1 ou 2. 

  Ce qui, en outre, distingue ces deux tables, aussi bien de celle d'Aristote, que de celle de Kant - malgré le mérite éminent de ces dernières - est leur absence de prétention à la complétude, prétention qui serait illusoire, étant donné le caractère d'exemplarité que revêt (dans sa définition même) tout paradigme linguistique. Rappelons pour mémoire la table d'Alcméon :

  Limite - Illimité

  Impair - Pair

  Un - Multiple

  Droite - Gauche

  Mâle - Femelle

  Stable - Mobile

  Droit - Courbe

  Clarté - Obscurité

  Bien - Mal

  Carré - Rectangle (Au sens gnomonique, où ces notions signifient : "égalité" - "inégalité"  des côtés du quadrilatère , et ne sont donc qu'une variante géométrique de la dyade logique "identité" - "différence" ou "même" - "autre". En remarquant  que ces notions, ici, peuvent également être dérivées des catégories arithmétiques Impair - Pair et Un - Multiple.)
  

     

    

   

   

   

   VI. LA MONADOLOGIE

   

   

  Objets premiers et objets monadiques

   

  A la série des objets premiers de la géométrie, construits par l'addition de monades, correspond, dans son ordre, la série des objets monadiques, construits, eux, par déformation ou transformation de la monade; série dans laquelle s'applique, là aussi, la contrainte pythagoricienne de dualité, exigeant que soit corrélée à la définition des objets géométriques, celle des actions, ou des opérations de pensée qui les engendrent.

   

  poser - point

  étirer - segment

  étaler - disque

  gonfler - boule

   

  Cette série d'objets se distingue de la première par deux traits essentiels; (d'une façon qui est totalement indépendante du fait que les deux séries possèdent deux objets en commun). D'une part, ses éléments ne peuvent être appelés "objets" qu'en un sens relatif, et par une transposition analogique, puisque, au sens strict, et au regard de leur commune unité arithmétique, ces objets ne correspondent pas réellement à des êtres mathématiques différents, mais bien plutôt à différents états d'un seul et même être qui est la monade : "monade posée", "monade étirée", "monade étalée", "monade" gonflée; de sorte que la série entière des objets monadiques se trouve n'occuper que le seul premier rang, ou ne concerne que le premier objet, de la série des objets premiers. En second lieu, dans cette série, les actions 3 et 4 ne sont pas dépendantes de celles qui les précèdent immédiatement, mais sont conduites directement à partir de la première. Ce second point entraîne d'importantes conséquences.
  

  La contrainte pythagoricienne de dualité revient, en pratique, à attribuer à chaque objet géométrique une coordonnée de temps. Or, alors que la série des objets premiers se développe et parvient à saturation en quatre temps d'action enchaînés, la série des objets monadiques sature à chaque fois, elle, en 2 temps d'action seulement; - c'est-à-dire que son degré d'universalité mathématique est d'un ordre comparable à celui de la dyade indéterminée, qui est celui d'une saturation binaire généralisée.

  En mathématique pythagoricienne, le fameux problème de la quadrature du cercle apparaît avant tout comme un problème mal posé, parce qu'il tente de faire coïncider un objet occupant le rang 3 d'un ensemble systématique saturant à 4, le carré, avec un objet qui est logiquement saturé à 2, le disque, et qui appartient à un ensemble systématique ne comprenant d'ailleurs que des positions saturées  de type "1" ou "2", qui est celui d'un ordre correspondant à une expression immédiate et directe de la dyade indéterminée, au sens précis, et réducteur, où le "dyadique" peut se traduire en simple "binaire", ou encore, au sens où l'indéfinité mathématique qui caractérise cette structure, peut être confondue avec la notion logique simple de maximité.

  L'idée revient de façon lancinante dans la tradition pythagoricienne, que la monade et la dyade indéterminée engendrent tous les nombres, ce qui, en bonne compréhension pythagoricienne, revient presque à dire : tout le reste de la mathématique. Cependant, concernant l'antériorité hypothétique de l'une par rapport à l'autre, il convient d'être plus circonspect, car les deux peuvent apparaitre comme coéternelles relativement en tous cas à la mathématique, par le seul fait qu'elles lui sont antérieures et ascendantes, et relèvent d'un ordre réellement plus universel, ou proto-logique. Dans l'ordre dont il s'agit, on peut simplement poser en principe que la dyade indéterminée représente le principe universel de l'ordinalité, et la monade, celui de la cardinalité. Or ces deux notions ne sont, au nombre et à la mathématique, rien de moins que ce que sont une mère et un père; de sorte qu'il est impossible à cette science de les isoler l'une de l'autre sans y perdre son appui premier, son existence même, comme on le voit, par exemple, dans la structure du gnomon, où à chaque cardinal impair correspond une paire d'ordinaux (respectivement Entier et Carré), et comme la monadologie l'illustre de façon tout aussi exemplaire; puisqu'en effet :
  

  On peut remarquer que, dans la série des objets monadiques, c'est l'objet qui est toujours le même, et l'opération chaque fois différente; tandis que, dans la série des objets premiers, l'objet est à chaque fois différent, mais l'opération ("poser un point") demeure toujours la même. Donc, d'une part, la série monadique et la série additive des objets premiers peuvent nous paraître constituer, ensemble, un cas d'application des plus universels de la dyade indéterminée; dans lequel la série monadique occupe la position de l'un et du même, et celle des objets premiers, celle du multiple et du différent; mais d'autre part, chacune de ces séries se présente elle-même individuellement comme une application secondaire de cette même dyade indéterminée, dans une situation cette fois, où chaque terme, chaque pôle de la dyade, échange dialectiquement sa position avec celle de son antagoniste.

   

  série monadique (objets monadiques)...................UN (même)

  objet un - opérations multiples

   

  série additive (objets premiers).............................MULTIPLE (différent)

  objets multiples - opération une
  

   

  Ces considérations, il est vrai, semblent donner raison à Granger dans sa conviction que la dualité "opération-objet" puisse constituer une catégorie plus essentielle à la mathématique que les autres. En effet, en tant qu'elle serait le véhicule de la continuité ou de la "retroussabilité" indéfinie de cette science, elle apparait aussi comme le principe qui permet, comme ici, à deux valeurs "polaires" de la dyade indéterminée de permuter et d'échanger leurs positions, - positions qui, en dehors de ce processus, apparaissent toujours "figées" de proche en proche par une puissante contrainte ordinale qui les détermine à s'"avouer" première ou seconde. Par ce côté, la dualité opération-objet peut légitimement apparaître comme le "moteur immobile" de la mathématique, comme le vecteur et l'incitateur constant de sa possibilité interne de croissance, de développement indéfini.
  

   

   

   

  La synthèse des objets monadiques et la représentation mathématique de la situation naturelle de l'homme.

   

  Tout comme la série des objets premiers peut être rassemblée synthétiquement dans les dix points de la tétractys, où chaque objet correspond biunivoquement à un étage ou un rang déterminé de cette structure, la série des objets monadiques peut, elle aussi, être reccueillie synthétiquement dans une seule pensée, mais il est à remarquer que, parmi les formes que peut revêtir cette représentation synthétique, il en est une qui l'emporte décisivement sur les autres, de par sa relation avec une certaine description mathématique de la situation naturelle de l'homme. Et ce, comme on va le voir, selon trois plans d'universalisation différents de cette situation ou "nature" humaine, correspondant à trois degrés cosmologiques différents de son développement logique universel.
  

  Un point de mathématique précisé par René Guénon revêt ici une importance fondamentale, qu'il convient de remémorer.
  

  En tout point de l'espace, il ne passe qu'une seule droite verticale, mais une indéfinité de droites horizontales; tandis que, dans le même point de l'espace, il ne passe qu'un seul plan horizontal, mais une indéfinité de plans verticaux. Ce qui signifie pour nous que les dimensions 2 et 3 de l'espace pythagoricien, ou encore les "objets" 2 et 3 de la série des objets monadiques, se trouvent, dans la situation de l'homme, déjà montrées, distinguées, voire exemplifiées par la structure de l'espace lui même.

  La représentation synthétique la plus naturelle de la série des objets monadiques consiste donc à matérialiser, dans une sphère de dimension indéfinie (objet 4), d'une part, un axe polaire vertical (objet 2), et de l'autre, un plan discoïdal horizontal orthogonal à celui-ci (objet 3), sans oublier le point central (objet 1), situé à l'intersection de ces deux derniers objets, qui est à la fois l'origine et le centre géométrique de chacun des trois autres membres de la série.

   

  

   

  La boule est donc le seul objet monadique dont on puisse dire de plein droit qu'il est le gnomon du point qui est son centre (en supposant que ce point puisse être soustrait du volume de celle-ci)  puisqu'il est le seul dans lequel les possibilités de développement du point s'expriment en tant que totalité clôturée.

  C'est le même symbolisme fondamental qui est ensuite reporté, naturellement, dans la représentation de la situation de l'homme par rapport à la terre, selon toutes les applications que peut comporter le symbolisme des 6 directions de l'espace, où l'axe vertical correspond tantôt à l'axe haut-bas, tantôt à l'axe zénith-nadir, tandis que le plan horizontal correspond à celui déterminé par la structure d'une croix, formée, dans un cas par les axes "droite-gauche" et "devant-derrière", dans l'autre par les axes "nord-sud" et "est-ouest"; ce symbolisme se reporte  ensuite, de manière identique, dans les représentations de l'orientation de la terre dans l'univers, où alors l'axe vertical peut être soit l'axe polaire nord-sud, soit celui de la rotation de la terre, tandis que le plan horizontal pourra être, selon le cas envisagé, celui de l'équateur, celui de l'écliptique, ou tout autre plan de même nature. Dans toutes ces représentations sont donc privilégiés un certain axe polaire vertical, représentant en quelque sorte "électif" de la dimension pythagoricienne "2" ou de la droite, et un certain plan discoïdal et horizontal correspondant (qui n'est au fond horizontal qu'en raison de la "verticalité" hypothétique de son prédécesseur "polaire", en vertu d'une relation de dépendance purement logique et relative), plan habituellement divisé en "quartiers" par le moyen de deux axes orthogonaux entre eux et formant une croix horizontale, qui se présente de façon similaire comme un représentant "électif", ou supérieurement exemplaire, de la dimension pythagoricienne 3. Ces réalités sont en effet privilégiées parce qu'elles correspondent, très simplement, et sans aucun reste, au tableau logique quaternaire de la situation naturelle de l'homme, et à son "transport" ou à sa transposition analogique à différentes "échelles" de la nature cosmique. Chacune de ces représentations a pour résultat de définir un espace "euclidien" clos et complet, entièrement paramétrable, coïncidant avec la possibilité d'expansion indéfinie du sphéroïde de rang 4, en fonction d'un point qui est son centre (objet de rang 1), point qui peut lui-même être défini par l'intersection des objets de rang 2 (axe vertical polaire) et 3 (plan discoïdal horizontal). Ceci méritait d'être précisé pour ceux qui se demanderaient encore si cette représentation géométrique et synthétique quaternaire des objets monadiques, constituant une application directe de la tétractys, pouvait d'aventure relever d'une quelconque "convention", au sens d'une décision arbitraire et souveraine. Car la tétractys n'est pas, en effet, une construction intellectuelle forgée par un quelconque acteur individuel de "l'histoire des sciences", mais une réalité naturelle dans laquelle l'homme se découvre, ou se reconnaît plongé à tout instant, parce qu'il la rencontre à la racine même des idées qui sont en lui.

   

  

   

  Bien qu'il soit impossible de leur donner ici un développement complet, on peut donc décomposer comme suit les moments logiques selon lesquels se forme la notion mathématique de l'espace naturel.
  

   

  Niveau 0. Mathématique. Degré de la possibilité pure a priori            (vertical) - (horizontal)

   

  Niveau 1. Situation gravitationnelle et chirale de l'homme         (haut-bas) - (droite-gauche-

                                                                                                                       devant-derrière)

   

  Niveau 2. Situation de l'homme par rapport à la terre       (zénith-nadir) - (nord-sud-est-ouest)

   

  Niveau 3. Situation de la terre par rapport à l'univers     (tout axe polaire ou de rotation ou de

                                                                      révolution) - (tout plan horizontal correspondant)

   

  Il faut remarquer ici que ce qui est premier dans l'ontogenèse, à savoir le degré zéro qui est celui de la possibilité universelle, est en réalité dernier dans la chronogenèse, c'est-à-dire dans l'histoire effective de la connaissance humaine, puisque ce n'est que de la considération des conditions naturelles détaillées aux niveaux 1, 2, et suivants, qu'a pu se former, dans la culture intellectuelle de l'homme; la notion du degré de la possibilité a priori, qui est celui exprimé par le point de vue mathématique. Dans l'ordre logique qui est celui de la formation de la connaissance, le degré zéro n'est donc réellement qu'un résultat exprimé, ou abstrait de la seule consistance ou coïncidence synthétique de la suite des moments qui lui succèdent, suite dont le départ est seul connu d'une façon que l'on peut dire familière, mais qui, à l'échelle où nous l'examinons ici, demeure bien évidemment indéfinie quant aux possibilités d'extension ou de clôture offertes par son développement cosmologique.
  

   

  En raison même de sa quotidienneté, on ne remarque pas assez le caractère profondément original de ce symbolisme, puisqu'en définissant l'homme comme un segment vertical, il a pour conséquence de faire de lui un cousin de l'arbre, voire à sa limite idéale, du fruit, et en tous cas un être davantage placé sous le régime de la croissance végétale, qu'une forme apparentée à la généralité du règne animal, - à moins de descendre, dans celui-ci, jusqu'à un degré de primordialité qu'on qualifiera de "cytologique", la cytologie ayant d'ailleurs réellement ce caractère d'une monadologie appliquée. On peut dire de la cytologie qu'elle est, relativement à la monadologie (pythagoricienne, s'entend, c'est-à-dire "indéfinitésimale"), ce qu'est la cristallographie relativement à la théorie des objets premiers, et plus généralement à la notion pythagoricienne de symétrie d'objets construits par addition de monades : un exemple d'application quasi immédiate de la nature mathématique, à la nature physique. Nous disons quasi-immédiate, car naturellement, ces applications physiques de la loi mathématique n'ont, dans un cas comme dans l'autre, qu'un degré d'exactitude "statistique" ou "approximatif" (pour reprendre l'expression de Gell-Mann : à gros grains); ce qui n'affecte en rien leur validité, car, comme l'a montré Granger, et comme le savait aussi Pythagore, le vague, l'à-peu-près et le grossièrement défini, ne sont pas pour la mathématique des maladies originelles, mais des conditions aux limites positivement instituées, et assumées de l'intérieur par cette science (en tant que nécessaires à l'expression même de ce qui importe), avant même qu'elle ne s'avise de légiférer sur les conditions de possibilité de la nature physique.

   

   

   

   

   

   

  VII. LA THEORIE GENERALE DU SIGNE

   

   

   

  Le tenseur binaire radical

   

  Lorsqu'on la représente par la lettre V, la dyade indéterminée apparaît morphologiquement analogue au tenseur binaire radical de la linguistique guillaumienne, concept que cette théorie définit comme "l'opérateur universel de la structure du langage". La linguistique guillaumienne se distingue des autres écoles linguistiques par sa visée synthétique. Ce qui l'intéresse n'est pas, prioritairement, l'analyse architectonique du "système de la langue", mais un fait linguistique plus profond, agissant à chacun des niveaux de ce système, que son auteur qualifie de "psychomécanisme", ou, ailleurs, de "mécanisme de puissance de la pensée humaine". Il s'agit donc d'un opérateur antérieur à la problématique propre du langage et du signe, puisqu'il se rapporte, plus originairement, à la parole, en tant que geste et action entière de l'homme, non encore décomposée. Citons Gustave Guillaume :

   "La pensée tient sa puissance de ce qu'elle est habile à particulariser et à généraliser. Privée de cette double aptitude - qui constitue un entier (un entier intérieurement binaire) - la pensée serait sans force et inopérante. Or, si de ces deux opérations - particularisation et généralisation - desquelles la pensée tient sa puissance, on ne retient abstractivement que ce qu'elles comportent de mécanique, elles se réduisent à deux mouvements de pensée, l'un allant du large à l'étroit, (inhérent à la particularisation), l'autre allant de l'étroit au large (inhérent à la généralisation). Une réduction abstractive infléchie selon la pente arithmétique ramènerait la particularisation à un mouvement allant du plus au moins, et la généralisation à un mouvement allant du moins au plus. Le mécanisme de puissance de la pensée, c'est l'addition sans récurrence, sans retour en arrière, de deux tensions, une tension I fermante progressant du large à l'étroit, et une tension II ouvrante progressant de l'étroit au large, soit figurativement :  

   

   

  A ce mécanisme de puissance, on a, dans cet ouvrage, donné le nom pleinement justifié de tenseur binaire radical."

  L'analogie entre ces deux notions : dyade indéterminée, et tenseur binaire radical, n'est en rien superficielle, mais, au contraire, tout ce qu'il y a de plus profonde; puisque ces deux notions constituent à nos yeux les fondements opposés, mais complémentaires, d'une discipline bipartite qui est la théorie générale du signe. La théorie générale du signe est un point de vue depuis lequel on considère les systèmes de signes, ou encore, les paradigmes*, tels que, pour s'en tenir à un niveau élémentaire, les alphabets et les gammes musicales, comme formant eux-mêmes de "gros" signes unitaires et organiques, comme de pures singularités morphologiques. Dans cette théorie, on s'efforce d'appréhender d'un point de vue extérieur et équidistant, (il s'agit d'une théorie générale et non synthétique), d'un côté, le nombre, à savoir, en l'espèce, des systèmes de signes, tels que les gammes musicales, qui sont issus de l'intuition d'une quantité mathématique discrète, et qui reposent donc sur un fondement stable et éternel, "a priori", sur un rapport intuitif et immédiat au même, à l'identité du nombre; et de l'autre, le verbe, ou le signe linguistique, dans toute sa naturalité, sa contingence initiale, son "instant d'arbitraire", qui fait qu'aucun nom, d'aucune langue, ne sait nommer les choses exactement dans la même "guise" qu'un autre. Or le tenseur binaire radical, dont l'ambition est de réduire le processus de la signification à un mécanisme universel, a précisément aussi la charge d'expliquer la genèse concrète, matérielle, du signe linguistique; et cet opérateur semble bien recéler cette capacité insigne, de savoir exhiber à la fois l'universalité, la constance, l'unicité du geste linguistique, et sa parfaite contingence ou déterminité naturelle, puisqu'il se distingue par ses applications spectaculaires à des faits de langue précis et localisés, tels que, par exemple, le système de l'article français, ou celui de la flexion nominale. 

   

  Le système phonologique des consonnes du français.

   

  Le tenseur binaire radical est efficient, pour commencer, dès le premier degré de la morphogenèse du langage, celui de la constitution du système phonologique, qui s'effectue par la transformation du continuum acoustico-vocalique de la phonation, en un champ d'unités discrètes : les phonèmes. Les tensions 1 et 2, "fermante" et "ouvrante", y jouent alors, très précisément, le rôle que jouent, dans le système morphogénétique de Turing, les fonctions chimiques, ou morphogènes, "inhibiteur" et "activateur", dont on sait qu'elles engendrent, en phase d'équilibre, des réseaux de gros points distribués en symétrie hexagonale; ce qui explique, comme nous allons tenter d'en exposer brièvement la raison profonde, l'omniprésence des structures hexagonales et des relations logiques biternaires dans la plupart des systèmes phonologiques.

    

  

  structures de Turing, avec à gauche, phase d'équilibre hexagonal

    

  La structure phonologique la plus caractéristique est une structure de type "sceau de salomon", dans laquelle une relation ternaire faible, ou secondaire, est posée en tempérance immédiate d'une relation binaire forte, ou première. Dans la morphogenèse d'un système, la première différence constructive est, par définition, toujours binaire, mais il faut bien comprendre que le binaire est, fondamentalement, l'opérateur le plus impropre à la construction du continuum; ce que l'on peut illustrer sur le plan de la logique première, en remarquant que le segment, parce qu'il est la première différenciation de la monade, est aussi l'objet monadique qui ressemble le moins au point; et en effet les objets monadiques de rang 3 et 4, le disque et la boule, ressemblent plus au point que le segment. La relation ternaire joue donc le rôle de tempérance maximale de la relation binaire, - ou si l'on veut, de médiété - tempérance qui permet à une relation d'opposition binaire de se rapprocher le plus vite d'un envahissement général du continuum. Ainsi, dans le système phonologique des consonnes du français, les relations binaires fortes sont les relations "sourde/sonore" et "occlusive/fricative"; tandis que les relations ternaires se disposent en médiation (dentale/labiale/gutturale), ou en extension (nasale/liquide/semi-voyelle) de ces relations binaires fortes.

   

  

    

  (Remarques.

  1. Par souci de simplicité, les phonèmes sont ici désignés biunivoquement par des lettres de l'alphabet, qui, comme on le sait, sont souvent plurifonctionnelles. Pour être correctement interprétées, les lettres doivent être ici oralisées dans le paradigme "a"; c'est-à-dire que, pour connaître la valeur exacte des phonèmes du tableau ci-dessus, il suffit de faire suivre les lettres qui les désignent par la lettre "a"; ainsi, pour préciser les cas litigieux : "carte" et "garde" pour les occlusives "c" et "g", "wapiti" et "yak" pour les semi-voyelles "w" et "y", "chat" et "sable" pour les phonèmes "ch" et "s", "zazie" pour "z", etc.)

  2. Contrairement à l'opinion de divers linguistes, aucun phonème du troisième niveau n'est inclus dans la catégorie "sonore". Même si nous avons pu constater que certains linguistes demeuraient réticents au principe autoritaire de la logique, la catégorie "ni sourde ni sonore" constitue pour nous une catégorie indispensable du système, pour une raison simple, qui est que la relation sourde/sonore constitue un ensemble biunivoque parfaitement compact. En effet, une sourde se transforme univoquement en la sonore correspondante par "sonorisation"; et réciproquement, une sonore se transforme en la sourde correspondante par "assourdissement". La catégorie "ni sourde ni sonore" désignant dès lors, ni plus ni moins, l'ensemble des phonèmes qui sont exclus de cet ensemble biunivoque compact.

  3. Ce tableau constitue, bien évidemment, un système complet des consonnes du français, définies selon la méthode jakobsonienne de permutation de la syllabe. Il recense donc l'ensemble des solutions "c" existant, en français, pour remplir une matrice de syllabe à deux éléments simples  (c : Consonne / v : Voyelle). La lettre X, comme on le sait, ne correspond pas à un phonème, mais à 4 phonèmes différents, les deux sourdes de Félix (cs) et les deux sonores de Xavier (gz); cette lettre signalant donc, par sa fonction comme par sa forme, le centre géométrique du paradigme sourd/sonore. La lettre "k" est un substitut phonologique de "c". Enfin la consonne manquante de l'alphabet français, la fricative "ch" de "chat", est ici "représentée" par le graphème "inutile", non phonologique, de ce même alphabet : la lettre H; car, comme l'a indiqué Saussure, on ne peut en aucune manière appeler "phonème" un signe qui n'a d'autre existence phonétique, que le fait qu'on ne puisse faire, devant lui, ni liaison ni élision.

  4. Voyelles. Il n'existe pas de système constant des voyelles du français. Leur dénombrement même est impossible, étant sujet à des variations locales. Ainsi, les voyelles finales des mots "chacun" et "demain" correspondent à des phonèmes identiques à Paris, mais distincts à Toulouse. Pour les voyelles des mots "chauve" et "porte", c'est l'inverse : elles correspondent à des phonèmes identiques à Toulouse, mais distincts à Paris. Le français apparaît donc, à cet égard, moins différent qu'on pourrait le penser des langues sémitiques, dans lesquelles les voyelles sont réputées n'avoir pas d'existence véritablement individuelle. En revanche, le système des consonnes est rigoureusement constant, quelles que soient les différences d'accent ou de réalisation locales. Le phonème "r" peut-être roulé ou non selon les régions, il reste fonctionnellement un "r", c'est à dire qu'il conserve partout la même fonction dans le système.)

    

  Si maintenant toutes ces relations biternaires sont déployées, ou libérées, non plus dans le champ logique bidimensionnel qui est celui d'un tableau analytique, mais dans un espace de diffusion "théorique" tridimensionnel, on s'aperçoit qu'elles se solidifient spontanément en un prisme hexagonal. Pour passer d'une structure à l'autre, il suffit d'enrouler en pensée le plan du tableau ci-dessus, en mettant bout à bout ses côtés gauche et droit.

   

  

    

  Ce que l'on pourrait commenter ainsi : les relations logiques biternaires de type "sceau de salomon" constituent l'opérateur de différenciation le plus rapide et le plus efficace pour transformer un "segment" (c'est-à-dire une relation d'opposition binaire) en un "disque" (hexagone), puis en un "cylindre" (prisme); ou encore, pour permettre à cette relation d'opposition d'envahir l'espace à trois dimensions.**

  Pour que le modèle mécanique guillaumien soit opérant, il faut donc considérer que la tension 2, la tension ouvrante, est la tension binaire, ou "paire", tandis que la tension 1, la tension fermante, est la tension ternaire, ou "impaire". En effet, le ternaire étant toujours polarisé par un centre de symétrie qui est structurellement son origine, (centre correspondant ici aux catégories "labiale" d'une part, et "liquide" d'autre part) une tension ternaire peut être "fermante", ou "inhibitrice", lorsqu'elle est, géométriquement, une tension de contraction du segment (2) vers le point qui est son centre (1); ou bien, si l'on raisonne sur un triangle, une tension de contraction de ce triangle, régressant géométriquement de l'un de ses côtés (2), vers le sommet opposé (1).

   

  

   

  La structure complète du système des consonnes pouvant dès lors se déployer en trois coups de temps seulement, trois entiers guillaumiens, ou trois "guillaume" correspondants aux trois étages de la structure ci-dessus; car nous attachons pour notre part le plus grand prix à cette propriété du tenseur binaire radical, un peu négligée par les guillaumiens et peut-être par G. G. lui-même, de permettre une expression quantifiée, et en ce sens véritablement scientifique, de la différence énergético-informationnelle dans laquelle consiste ultimement le signe. Notons que ce modèle apparaît en tout point conforme au formalisme logique de la dyade indéterminée, dans lequel l'impair, le fermé, précède toujours le pair, l'ouvert.

   

  Notons que l'ensemble du système peut, à son tour, faire l'objet d'une résolution ternaire "fermante", ou "inhibitrice", analogue à celles qui opèrent à chacun de ses étages (au prix de l'ajout, dans le décompte des temps du système, d'un temps de genèse supplémentaire, logiquement antérieur aux trois moments dénombrés ci-dessus); à cette réserve près que, dans une telle application, c'est l'étage inférieur, le "ni-ni", qui devrait plutôt occuper la position centrale, et donc le niveau médian de la structure, puisque ce connecteur logique correspond bien réellement, dans le formalisme de la dyade indéterminée, au pôle de l'imparité et de la fermeture, qui ici, s'oppose à la parité et à l'ouvert de l'ensemble biunivoque "sourdes et sonores". Précisons que la disposition adoptée dans les figures ci-dessus résulte uniquement de la contrainte bidimensionnelle de la logique de tableau (logonique), adoptée ici par simple commodité et en raison de sa richesse analytique. Mais la représentation suggérée dans le présent paragraphe apparaît préférable d'un point de vue synthétique, en ce qu'elle permet d'exprimer le système, non plus sous la forme du quasi-cylindre (prisme), mais sous celle du sphéroïde ou de la quasi-boule topologique, en assignant à l'ensemble hexagonal "ni-ni" la fonction topologique d'un disque équatorial, et aux ensembles "sourdes" et "sonores" celle, logiquement seconde, de disques tropicaux, respectivement nord et sud. Or la représentation sphérique, en raison de sa nature monadique, correspond, comme on le verra plus loin, à l'expression mathématique optimale du processus d'envahissement constructif du continuum perceptif, dans lequel consiste toute la nature du signe linguistique matériel.

   

   

   

  *
  

   

  Le choix, par Gustave Guillaume, d'un modèle mécanique, plutôt qu'un modèle chimique ou autre, est, à lui seul, assez lourd de conséquence. Il peut se réclamer d'un certain principe d'économie scientifique, qui est celui du "moindre besoin". La science trouve toujours meilleur ce qui est fait avec des moyens plus "rustiques", lorsque ceux-ci s'avèrent suffisants. Mais surtout, le choix d'un modèle mécanique a pour effet de placer, par hypothèse, l'organe du langage - ou si l'on veut, son centre organisateur - beaucoup plus près du corps et de son activité mécanique, sinon musculaire, que du cerveau, et de son activité chimique ou électrique.

   

  *

  Ces deux notions, dyade indéterminée et tenseur binaire radical, nous représentent donc les deux visages, ou les deux côtés du signe; un côté qui implique, originairement, passivité, prudence, patience ou réceptivité, (la tétractys, par exemple, est essentiellement un "récipient", ou un "réceptacle", pour reprendre la terminologie technique du Timée), et qui est tourné vers ce qui est stable, constant, et éternellement le même, vers le nombre; et un autre côté qui consiste, originairement, en une action, en un engagement en quelque sorte libre, souverain, ou créateur, dans la matière, avec tout ce que cela comporte de "hasard heureux" et de "chatoiement" poétique de l'être, et qui est la parole, en tant que geste et action générique de l'homme. La connaissance pythagoricienne n'étant qu'un accord, ou une harmonie, entre cette naturalité et cette éternité. Car ces deux côtés du signe ne peuvent jamais, en effet, être séparés complètement l'un de l'autre, puisque même le nombre, pour être reçu, doit d'abord être saisi par l'entremise d'un nom. Inversement, on a vu, avec Gustave Guillaume, que l'opérateur le plus profond de la langue se réduisait, en définitive, à un infléchissement arithmétique, à une espèce de tendance à "imiter" le nombre.

   

    

  Systèmes d'orientation, gammes et calendriers

   A la famille des systèmes "mathématiques" appartiennent également les systèmes relevant du paramétrage de l'espace temps, tels que les systèmes d'orientation et les calendriers. Les problèmes de "comma" musical sont, mathématiquement, analogues à ceux posés par le comput calendaire. La tendance à une stabilisation hexagonale ou dodécagonale - en considérant que ces diverses divisions du temps peuvent être représentées par des divisions du cercle - demeure, néanmoins, assez générale à ces systèmes (gammes et calendriers). Le système babylonien, conservé par la civilisation moderne, est sexagésimal; l'année, comme le zodiaque, comme la journée, et comme l'heure de nos horloges, a 12 divisions; et notre système musical, après une computation interne de plus de deux mille ans, s'est stabilisé en une gamme tempérée de 12 demi-tons, soit 6 tons entiers.

    

  Les couleurs

  D'autres systèmes, enfin, appartiennent à une catégorie intermédiaire; ainsi, les systèmes de noms de couleurs internes à chaque langue naturelle qui, bien qu'ils relèvent de la contingence linguistique, réalisent, la plupart du temps, un paramétrage mathématique à peu près idéal, et quasi constant, du spectre de la couleur. Les mêmes "stations" se rencontrent, à quelques nuances près, dans la plupart des idiomes occidentaux, permettant une transmission relativement aisée, d'une langue à l'autre, de l'expérience de la couleur, pourtant incommunicable par nature, en l'absence d'un référent universel et non subjectif. "Les couleurs", en effet, n'existent pas, puisque la couleur est originairement un phénomène singulier, un continuum. Le bleu n'est, en soi, rien de plus que la somme des expériences et des idées humaines qui se sont accrochées au mot "bleu", depuis que ce mot est utilisé. Le référent des couleurs que nous avons l'habitude de nommer comme des individus, n'a donc, en toute rigueur, aucune existence absolue en dehors des noms naturels qui en fixent la notion. Son concept ne se "substantialise" que par un va et vient à la vérité fort subtil, dans lequel entrent en jeu, simultanément : 1) la consistance topologique intrinsèque, originairement locale, du seul système de signes - le système des noms de couleurs - qui, par sa vertu propre d'opérateur de différenciation, détermine ces signes, dans leur usage, tantôt à s'attirer, tantôt à se fuir magnétiquement de proche en proche, par un mouvement devant normalement les conduire, dans leur devenir utilitaire, à se satelliser à une distance étalon de valeur 1 les uns des autres; et 2) la confrontation permanente de ce même système avec l'expérience quotidienne, qui amène la notion de ces signes à "s'infuser" graduellement de réalité ou de substantialité empirique, par un  mouvement de reconnaissance par "approches", ou par une "approximation" perceptive***; - ces deux mouvements, pour finir, se soutenant et se guidant l'un l'autre. Dans la genèse concrète du système, on peut imaginer que ce dynamisme, ce mouvement "optimiste" de la signification, puisse commencer à s'activer à partir d'un graphe rudimentaire de, par exemple, 4 ou 5 unités, dont la structure ou la configuration définitive demeurerait, dans un premier  temps, indécise, ou fluctuante; c'est à dire que l'on peut imaginer une langue primitive qui ne disposerait que de quatre ou cinq noms de couleurs. En revanche, nos systèmes modernes relèvent probablement d'un lent processus de "décantation" statistique, ou économique, de nature essentiellement pratique.

   

   

  Structure "sablier" du paradigme français des noms de couleurs.

   

  Triangle "Mondrian". Couleurs dites "primaires" (Rouge-Jaune-Bleu)

   

  

   

    Triangle "Malévitch". Couleurs dites "alchimiques" (Rouge-Noir-Blanc)

  Chacun des "registres" du sablier enferme virtuellement une structure hexagonale biternaire de type "sceau de Salomon". En outre, la structure générale du sablier lui-même est topologiquement analogue à la structure "fermante-ouvrante" du tenseur binaire radical; de sorte que le système peut nous apparaître comme formant un "super-entier" guillaumien fermant-ouvrant,  composé en réalité de deux entiers conjoints ou "siamois".
  

   

  Ce paradigme linguistique est, par exemple, rigoureusement identique à celui de la langue anglaise, où les onze stations du sablier (brown, black, grey, white, pink, red, orange, yellow, green, blue, purple) correspondent, comme en français, aux onze noms de couleurs qui sont statistiquement les plus utilisés. De tels paradigmes peuvent être qualifiés d'"optimaux", en ce qu'ils réalisent un compromis parfait entre une variété de contraintes empiriques, voire expérimentales, dont les unes sont optiques, telles que le paramétrage des "couleurs de l'arc-en-ciel", ou, plus exactement, de l'expérience visuelle de la décomposition de la lumière (triangle supérieur), et les autres physico-chimiques, telles que la fabrication de nuances "intermédiaires", par le mélange de matières, ou de pigments colorés "primaires" ou fondamentaux (ensemble du paradigme). 
  

   

  La même structure peut être déployée sur un axe continu, par exemple un escalier, sur lequel les stations fortes arrivent une fois sur deux. Ainsi, si l'on part du noir, les 5 stations fondamentales sont les stations impaires.

   

   

   

   En conclusion de cet aperçu sur la couleur, on peut remarquer que la relative impuissance des théories modernes de la couleur à cerner la véritable essence de cette dernière, résulte assez généralement de la conviction partagée (bien antérieure à la notion officielle - d'ailleurs falsifiée et infidèle à la véritable pensée de Saussure - d'arbitraire "pseudo-saussurien" du signe), que la couleur ne peut de toutes façons pas résider dans son nom, pour la raison que celui-ci ne peut être qu'un signe "arbitraire" ou "conventionnel", au sens assez banalement négatif et réducteur que peuvent revêtir ces deux expressions. Ce préjugé assez général a conduit les théoriciens modernes à chercher, tantôt à objectiver la couleur par quelque procédure expérimentale chimique ou optique, tantôt, à l'exemple de Goethe, à la résorber dans le registre subjectif de la pure sensibilité, sinon même de l'émotivité. Mais ce qui a échappé à tous, (y compris au pourtant très sagace Newton) c'est qu'une fois qu'on avait produit toutes ces "simulations" phénoménologiques de la couleur, on avait seulement montré les raisons de la couleur, ses motivations en quelque sorte externes et contingentes - mais toujours pas la couleur elle-même, dont le contenu possible était pourtant "connu" et déterminé depuis le début, puisqu'il résultait de la toute puissance productive, a priorique et en quelque manière magnétique, émanée de la seule hypostase originelle de son nom.
  

   

    

  De la consistance logique continue de la théorie du signe matériel, à travers la nature mathématique diverse de ses principaux continuums de référence.

   

  Un témoin significatif des conceptions qui étaient celles des pythagoriciens, en matière de théorie du signe, est ce fameux passage du Protreptique d'Aristote, où l'on compare les trois doubles consonnes grecques formées à partir de la lettre sigma, avec les trois accords fondamentaux de l'harmonie musicale, rapportés à l'unisson. Cette comparaison à laquelle le malheureux Aristote ne comprend goutte, parce qu'il ne saisit pas le point de vue depuis lequel elle est énoncée, est d'une profonde pertinence théorique, comme on peut tenter, ici même, de l'exposer en quelques traits; et elle n'est pas le seul témoin du haut degré de technicité et de rigueur formelle qu'avaient acquis les spéculations des pythagoriciens, en matière de théorie du signe.

  Mais avant d'entrer dans le coeur du problème, il convient d'évoquer certaines considérations générales concernant la théorie du signe, qui ne pouvaient être abordées avant que des exemples précis du genre de systèmes auquel cette théorie s'applique, fussent produits, ou extensivement définis.
  

   En tout premier lieu, il convient de se défaire de l'idée que puisse exister, dans la théorie du signe, un plan phénoménologique correspondant à celui de la pure sensation, ou d'une réception sensorielle absolument passive, dénuée de toute intentionnalité, de toute dimension active, telle qu'en subsument, le plus souvent, les catégories rigides de la psychologie moderne, quelques diverses qu'elles puissent être.
  

  Les différents continuums sur lesquels raisonne la théorie du signe matériel, ne sont pas à proprement parler des continuums sensoriels, mais bien plutôt perceptifs, c'est à dire qu'ils comportent tous un élément relevant d'une certaine "magnétisation" préalable, ou "intentionnelle" et par conséquent active de la sensibilité, transcendante à l'indéterminité purement "objective" du fait sensoriel. Cependant, ces continuums se distinguent entre eux par le fait de comporter, les uns par rapport aux autres, une plus ou moins forte "proportion" de réceptivité, de passivité, ou au contraire d'opérativité et d'activité.
  

  De la même manière, le point commun aux différents systèmes que l'on a envisagés ici, est de consister, chaque fois, en une action organique de structuration d'un certain continuum perceptif, par la constitution d'un système d'unités discrètes régi par des interrelations logiques (elles-mêmes assimilables à autant de "logoi", ou de rapports d'entiers pythagoriciens); cependant, ces continuums ne comportent pas nécessairement le même nombre de dimensions mathématiques "théoriques", comme on peut aisément s'en rendre compte à l'usage. En effet.
  

  Le continuum de la tonalité, abstraction faite de ses conditions de réalisation pratiques, peut être représenté par un axe mono-dimensionnel (dimension pythagoricienne 2)**** comme il l'est dans la représentation courante du langage, où il est symbolisé par un axe appelé tantôt "haut-bas", tantôt "aigü-grave", expressions qui ont des sens assez voisins. Le continuum de la couleur, avec l'expression de ses différences combinatoires biternaires de type "sablier", requiert, quant à lui, au moins deux dimensions (dimension pythagoricienne 3); c'est-à-dire que, même si l'expérience de la couleur pourrait, en théorie pure, être communiquée à un sujet ne connaissant que l'existence de deux dimensions, elle requiert au minimum cette capacité de percevoir un "écran", sur lequel puissent apparaître différentes "taches colorées". Enfin le continuum de la phonation se distingue à son tour de ces deux premiers exemples, en ce que sa définition ne procède pas d'une seule aire sensorielle (telle que l'"oreille" pour la musique, ou l'"oeil" pour la couleur, dans une acception anatomique volontairement vague de ces deux "organes" sensoriels) mais de l'interconnexion de deux aires sensorielles; car en effet, le continuum de la phonation n'est pas seulement vocalique, mais acoustico-vocalique, de sorte que, bien qu'il soit entièrement immergé dans le domaine de l'empirique et du perceptif, il résulte de la mise en correspondance de deux "aires" sensorielles antagonistes, l'une active, représentée par l'appareil phonatoire, l'autre passive, représentée par l'organe de réception des sons élaborés par ce dernier. C'est pourquoi les propriétés d'un système tels que celui des consonnes, ne peuvent complètement se déployer que dans une dimension théorique supérieure à celle du plan, par conséquent en dimension pythagoricienne 4.

  Le continuum de la tonalité peut apparaître, à cet égard, comme le plus passif, en ce qu'il est indépendant des conditions concrètes de sa production, que celles-ci puissent être actives ou non n'ayant aucune incidence en la circonstance. La musique est en effet la réception d'un rapport arithmétique absolument pur et constant, dont la saisie ne nécessite aucun "geste" ni "exercice" musical particuliers, pas plus qu'elle n'exige la connaissance consciente des valeurs numériques correspondantes aux accords musicaux, puisqu'elle relève d'un registre empirique plus profond que ceux-là, que l'on peut légitimement qualifier de "subconscient" ou, si on préfère, de supra-conscient, qui est celui, tout naïf ou naturel, du sentiment immédiat de l'accord ou de l'harmonie, du "juste" et du "faux".

  A l'inverse, le continuum acoustico vocalique de la phonation est dépendant de la coordination préalable d'un appareil de production, avec un plan de réception antagoniste; et de ce fait, il paraît intégrer une plus forte proportion d'opérativité, d'activité, voire de "gestualité", dans sa constitution matérielle même, que le continuum tonal.
  

  Ces divers points précisés, il paraît maintenant plus aisé de gloser le fragment pythagoricien du Protreptique d'Aristote.

  La saisie pythagoricienne considère les trois doubles consonnes grecques formées à partir de la lettre sigma comme constituant hypothétiquement l'axe vertical polaire du système des consonnes; en considérant comme point zéro ou origine polaire de ce système, la lettre sigma elle-même en tant qu'elle n'est coordonnée à aucune autre. Puis il établit une correspondance entre ces trois modes de coordination de la lettre sigma, et ces trois rapports de coordination de la note tonique que sont respectivement la quarte, la quinte et l'octave. Soit :

  0. Sigma - Ton

  1. Ksi  - Quarte

  2. Psi - Quinte

  3. Dzêta - Octave

  On peut remarquer en premier lieu que les trois niveaux déployés ici correspondent, en grec comme en français, au ternaire fondamental des points d'articulation de la phonation : guttural - labial - dental; et de cette manière le "retour" de la dentale originaire (sigma) dans le dernier rapport (la lettre dzêta étant une combinaison de deux dentales) peut en effet correspondre, terme pour terme, au retour cyclique, ou "hélicoïdal", de la position de l'origine (ton) dans le rapport d'octave. On peut en outre remarquer qu'en français aussi, l'axe polaire du système des consonnes coïncide avec celui qui traverse les doubles consonnes formées à partir de la lettre S : savoir la double-sourde de Félix et la double-sonore de Xavier, même si le français ne possède pas d'autres doubles consonnes naturalisées dans l'alphabet, et si dans le système propre à cette langue, le ternaire le plus fondamental est un ternaire différent de celui des points d'articulation.

  N'en déplaise à Aristote, une telle comparaison apparaît donc bien légitime, si on la considère, avec la méthode adéquate, sous l'angle scientifique particulier qui est celui de la théorie générale du signe, domaine, il est vrai, dont cet auteur assez peu mathématicien, ne soupçonnait probablement pas même la possibilité de l'existence.

    

  *En sympathie, pour une fois, avec les variations de l'usage moderne à ce sujet, le terme "paradigme" désigne, synthétiquement, dans nos pages, comme il le faisait, il me semble, dans la pensée des anciens, à la fois l'exemple, et le système de coordonnées, ou encore l'ensemble, dont cet exemple est un exemple; la consistance de notre travail permettant, chaque fois, de savoir dans quel sens il est utilisé. Pour employer une image, le terme paradigme désigne la roue d'un système, en tant qu'elle peut être représentée par chacun de ses rayons, ou mieux encore, en tant que la nature même d'une roue ne consiste, ou ne résulte, que de la possibilité qu'ont ses rayons de permuter, et de prendre la place l'un de l'autre

  **Pour être plus précis, la structure à trois étages du système phonologique des consonnes du français contient 2 ensembles de structure biternaire, ou "sceau de salomon" : l'ensemble "sourd" (t-p-c, s-f-ch) et l'ensemble "sonore" (d-b-g, z-v-j), et un ensemble de structure terbinaire, correspondant ici au rez-de-chaussée de la structure : l'ensemble "ni sourd ni sonore"  (n-m, r-l, w-y).
  

  ***Cette notion d'approche, ou d'approximation perceptive peut, à première vue, apparaître paradoxale; mais elle ne l'est que si l'on ne considère la perception que comme un fait absolument passif, calqué sur la rigidité du schéma psychologique moderne : émetteur - récepteur, ce qu'elle ne peut être en aucune manière dans l'ordre phénoménologique qui est celui de la couleur; puisqu'on peut poser en principe qu'un sujet n'a, a priori, aucune chance particulière de rencontrer dans son champ de perception du vert, du rose, de l'orange, s'il n'a, auparavant, activé en quelque manière le "tenseur" ou "l'attracteur" capable de motiver et de guider une semblable "rencontre", et dont le foyer ne consiste que dans l'idée abstraite de la couleur, dans son concept même.

  ****Précisons que nous ne parlons là que du continuum tonal absolument pur et a priori, indépendamment des systèmes d'unités discrètes que l'on peut définir à l'intérieur de lui; car, une fois mathématiquement qualifié, l'axe monodimensionnel de ce continuum devra nécessairement adopter la forme de l'hélice (ou de l'"escalier hélicoïdal"), afin d'exprimer la récurrence périodique des rapports harmoniques qu'il contient.

   

   

    

    

  VIII. LE NOMBRE N'EST RIEN D'AUTRE QUE L'ACTION DE NOMBRER

    

  Qu'est ce que le nombre?

  Le nombre est l'art de compter des oranges en les remplaçant par des noix, puis en supprimant les noix (pour ne plus considérer, par exemple, que la trace qu'elles ont laissé sur le sable). Le nombre est l'empreinte ou la signature des choses, comme celle des actions qui les ont produites. Le nombre est l'art de poser des objets indéterminés - des monades - en ne retenant que l'action de les poser. Le nombre n'est pas seulement poser, mais poser et conserver, poser en conservant le plan sur lequel les monades sont disposées. La monade n'est donc pas un objet parfaitement lisse, car même la première monade posée est pourvue de "phylactères" ou de "moustaches", qui sont les vecteurs, ou les tenseurs, de sa coordination et de sa conservation future dans un quelconque champ de consistance.

  Le nombre, dit Brouwer, est un coup de temps. Mais il faut préciser : un coup de temps qui a été enregistré, ou engrammé, pour être conservé avec d'autres.

  Les anciens étaient plus rigoristes que nous ne le sommes, en ne concédant le statut de nombre ni à l'unité, ni au zéro, ni à la dyade indéterminée, ni bien sûr à l'infini. La mathématique pythagoricienne proprement dite ne commence en effet qu'avec l'idée de Mi-lieu,  (ainsi, le gnomon, avec son milieu de référence qui est l'origine ou la graine, est une théorie de l'imparité en tant que fait mathématique primordial, pour laquelle l'imparité n'est pas une catégorie du nombre, mais une catégorie mathématique universelle dans laquelle tombent, originellement, aussi bien le nombre que la figure) ou encore avec les idées musicales de Mèse ou de Médiété : toutes situations dans lesquelles le vide, ou la virtualité continue de la dyade indéterminée, est déjà polarisé, en un point quelconque, par un centre de consistance - centre qui, en musique, se détermine en fonction du ton ou de la note tonique de valeur 1. Dans l'esprit des anciens, lorsque, par l'action de nombrer le nombre 1, commence réellement la mathématique, il existe déjà 3 choses : une dyade déterminée + un premier objet, lui aussi déterminé; par conséquent ce que la langue naturelle appelle le nombre 1 est en réalité le nombre 3. (Ou encore : le premier nombre, qui n'est autre que l'action même de nombrer, a déjà une structure triadique analogue à la lettre V ou au "coin" de l'écriture cunéiforme.) Mais un tel rigorisme nous astreindrait à séparer la mathématique de sa relation avec la langue naturelle. Chacun peut admettre, ou simplement postuler, que le nombre 1 des mathématiques n'est pas la même chose que l'Un de la métaphysique, de la même manière que le signe zéro en mathématique est une chose différente du vide ou du néant de la métaphysique.

  Le cas de l'infini est, en revanche, plus embarrassant, pour deux raisons principales. D'une part, il existe déjà une catégorisation naturelle de "l'infini" mathématique, et naturalisée dans cette science même, qui est l'indéfini. Par conséquent, la coexistence de ces deux termes dans la langue mathématique pourrait donner à penser que le terme "infini" contient réellement quelque chose de plus que de l'indéfini; présupposé dont René Guénon a démontré l'inconsistance dans ses Principes du calcul infinitésimal. L'infini mathématique ne contient en effet rien de plus que cela même que désigne la notion d'indéfini, porté à saturation par une hypostase purement logique, mais non mathématique, en ce qu'elle ne correspond à aucune espèce d'effectuation ou de réalisation intellectuelle. La deuxième raison est que si l'on naturalise le terme "infini" en mathématique, il ne resterait, d'un point de vue pratique, plus aucun mot français, pour désigner l'objet d'un genre de spéculation qui ne relève absolument pas des possibilités, des ressources propres de la mathématique, même si le symbolisme mathématique peut souvent lui servir de support.
  

  On pourrait nous objecter que le terme "indéfini" peut s'avérer, lui-même, d'un maniement délicat, en ce que la notion de limite définie d'une suite indéfinie correspond bel et bien, mathématiquement, à un seuil de clôture logique, associé à un certain rapport, et donc à un "logos" pythagoricien, qui confère à l'infini mathématique un statut analogue à ces autres positions logiques saturées du signe mathématique, que sont les "nombres" 1 et zéro. Toutefois, le cas de l'infini se distingue des deux autres, en ce qu'il ne peut s'effectuer que par un "saut" logique, un clignement de paupière qui sanctionne, irrémédiablement, l'extinction de la mathématique en tant qu'activité intellectuelle continue. Car on peut dire que la mathématique a, relativement à la science, une fonction comparable à celle que divers témoignages pythagoriciens attribuent au corps, relativement à l'âme, qui est d'être un poste de garde au sens épistémologique le plus fort, au sens d'une réalité qui, une fois posée, n'a pas vocation à disparaitre ensuite dans une occasion ultérieure, mais demeure désormais réellement là comme une chose continuellement subsistante.
  

  Cette difficulté d'ordre plutôt linguistique disparaîtrait donc si, à l'expression habituelle de "passage" à la limite, qui suggère l'idée, mathématiquement fallacieuse, d'une résolution par glissement continu, on substituait celle de saut à la limite, qui rendrait compte de façon bien plus exacte du caractère de rupture et de discontinuité qualitative que revêt cette opération, correspondant précisément au passage de l'indéfini au défini, passage qui n'a en rien le caractère d'une exhaustion effective (c'est à dire intellectuelle) de la nature du nombre, telle que l'exigerait bel et bien la notion métaphysique positive et pleine de l'infini, mais qui est au contraire une coupure et un retour à l'origine, un repli instantané vers sa racine définie.
  

  Quoiqu'il en soit de ces difficultés proprement linguistiques, la notion de passage à la limite  demeure, à nos yeux, la seule approche légitime pour circonscrire l'infini mathématique; car, pour ce qui est des définitions "ensemblistes" ou "logicistes" de l'infini, formulées par les Cantor, Russel ou autres Zermelo-Fraenkel, elles ne nous paraissent recéler, sous leur apparente diversité, que de très simples et très semblables définitions logiques, d'un caractère purement formulaire et opératoire, du nombre naturel, (non nécessairement entier, mais simplement analogue à l'entier), c'est-à-dire du nombre considéré en tant qu'action générique de pensée, intégrant dans sa substance même ce principe de récurrence indéfinie. Si la "découverte" de l'infini - qui n'est en fait que la redécouverte de l'eau tiède de l'indéfinité mathématique de Philolaos (apeiron) - par divers mathématiciens et philosophes du tournant des XIXe et XXe siècle, collégialement hypnotisés par l'idéologie progressiste de leur époque, a occasionné pour eux et subséquemment pour l'homme moderne un certain traumatisme historique, ce n'est que parce que la notion du nombre avait été auparavant vidée, par le préjugé candide de ces idéologues mêmes, de presque tout contenu substantiel, pour se réduire à quelque chose d'à peu près semblable au chiffre, ou à un pur signe conventionnel, comme elle peut l'être par exemple dans les "Fondements de l'arithmétique" de Frege, ouvrage qui n'est pas sans intérêt mais dans lequel il n'est, à la désillusion de son titre, à aucun moment question du nombre. En résumé, si la notion de "passage à la limite" - qui elle-même, précisons-le derechef, ne produit aucun objet mathématique différent de ce que contient la notion "philolaossienne" de défini, ou de limité (peras) - parvient, par un saut résolutif, à saisir l"'infini" mathématique par le seul côté où il soit possible de le faire, qui est évidemment le côté fermé, étroit, ou petit, de la dyade indéterminée, les tentatives de définition ensemblistes et logicistes de l'infini s'imaginent, elles, pouvoir le saisir par où il est logiquement impossible de le faire, savoir du côté ouvert, large, ou grand, de la dyade indéterminée, qui est le côté où ce prétendu infini se confond platement avec l'indéfinité du nombre naturel. Cette "redécouverte" par les modernes de ce qui ne relève donc que des propriétés éternelles du nombre naturel, a étonnamment suffi à susciter chez eux une réaction d'horreur métaphysique, voire, à son origine cantorienne, neuro-religieuse*, avouée par ses propres victimes sous l'appellation mathématiquement stupéfiante de crise des fondements; et elle est aussi la raison cachée de la fabrication par ces mêmes modernes, par une sorte de réflexe de défense "transférentiel" au sens freudien, de la fable historiquement aberrante d'une crise pythagoricienne des fondements, prétendument consécutive à la découverte, par les mathématiciens de cette école, de l'existence de grandeurs incommensurables... - fable à laquelle on n'accorderait pas la moindre attention si son succès ne s'était perpétué jusqu'à nos jours, bien qu'il paraisse difficile d'expliquer, à l'aune de cette historiette, comment ceux-là même qui ont formulé la première définition mathématique rigoureuse, et toujours en vigueur aujourd'hui, de la commensurabilité (symmetria), ont pu être assez naïfs pour ignorer son contraire : la non-commensurabilité; ou encore, comment ces mêmes pythagoriciens, pétrifiés par l'idée de l'incommensurabilité, ont pu être aussi les auteurs des premières démonstrations historiquement connues de l'existence de grandeurs incommensurables, cela dès le premier groupe pythagoricien avec Hippase de Métaponte, et jusqu'à la monstration magistrale de la spirale de Théodore, dont le principe consiste à installer ces quantités irrationnelles dans la tétractys.
  

   

  *

   

  Sur ces remarques se conclut notre enquête sur les idées mathématiques de Pythagore, en attendant, peut-être, de reprendre en des temps ou des lieux plus opportuns; car le pythagorisme nous paraît voué à rester, un certain temps encore, une idée neuve, au sens précisé par Leroi-Gourhan, où est nouveau ce qui vient d'être créé, et neuf ce qui n'a encore jamais servi.

    

  (11. 12. 2013)

                                                                                                                   
  

   *Il paraît légitime à une conception non-aliénée de la sagesse (conception qui, comprise dans toute son étendue, conduirait à considérer la compartimentation du savoir moderne, et la spécialisation du savant qui en résulte, comme des formes d'aliénation), de regarder comme un symptôme du caractère pathologique, sinon morbide, de certaines conceptions modernes de la mathématique, le fait, par exemple, que Cantor soit apparemment devenu fou pour avoir mal compris la signification de l'article "des" dans l'expression "des pommes". A moins qu'on ne puisse retenir comme un argument à sa décharge, l'hypothèse que la lecture de l'étude de Gustave Guillaume sur le système de l'article français, où est exposée cette notion qui n'a rien d'exclusivement mathématique, mais qui est aussi trivialement logique et même grammaticale, de l'interrelation des catégories du défini et de l'indéfini, aurait pu le sauver de l'hôpital, en lui évitant de "découvrir" dans la seconde de ces catégories un abime métaphysique et religieux, l'"infini", qui ne s'y trouve en aucune manière. Mais nous aurions pu, de façon tout aussi "indifférente", évoquer l'adhésion passionnée du même Cantor à la "théorie du complot" concernant la paternité des oeuvres de Shakespeare, qui, à tout philosophe de sens rassis, se présente à l'intelligence sous l'aspect repoussant du mensonge. En effet, nous pensons que toute personne saine d'esprit est réellement convaincue dans son estomac que Shakespeare est bien l'auteur des pièces de Shakespeare, de même que Molière est celui des pièces de Molière; car la même théorie du complot a fleuri, de façon indépendante, au sujet de ce dernier auteur, pour des raisons historiques qui seraient d'ailleurs intéressantes à éclaircir, car ces deux écrivains ont en commun d'être des acteurs, c'est-à-dire des saltimbanques ou des troubadours de tradition médiévale, auxquels un certain esprit académique et petit bourgeois du XIXe siècle a voulu dénier, de façon très autoritaire et au fond bien comique, pour ne pas dire "diafoiresque", la possibilité a priori d'être devenus de "profonds penseurs", des philosophes; de sorte que la fabrication historique de ces deux théories du complot s'avère renvoyer, de façon assez brutalement politique, à la séparation socratico-platonicienne de la poésie et de la philosophie, qui, dans les dialogues de Platon, a vu cette dernière s'instituer comme un bavardage "bourgeois", ou si l'on préfère "citoyen", (au sens étymologique de ces deux adjectifs, où ils sont équivalents au grec "politikè"), sans préjudice de son devenir "professionnel" et "académique", discours entièrement contenu dans les bornes de la raison dialectique, et bien différent dans sa nature de l'inspiration directe, supposée "subconsciente" ou "supra-consciente", du poète, (cela en dépit du fait que le genre dialogué se rattache encore, dans sa forme purement extérieure, à celui de la comédie) : - conception platonicienne de la philosophie qui est bien évidemment en rupture complète avec les conceptions orphique et pythagoricienne notamment, en la matière. Or les théories du complot ne sont, comme on le sait, qu'un banal marqueur logique de l'ignorance, et plus précisément, d'une forme spécifiquement moderne d'ignorance qui, plutôt que de s'avouer honnêtement ce qu'elle est, préfère se réfugier dans les croyances les plus absurdes. C'est pourquoi la rencontre avec une thèse ou une tournure d'esprit "complotiste" a réellement, pour la raison commune, une ressemblance avec l'expérience clinique de la confrontation avec la folie, telle que l'a décrite le psychiatre Minkowski, qui est la constatation immédiate, et "décourageante", d'un divorce avec le sens commun habitable. Et de fait, un auteur qui s'imagine, par ses travaux mathématiques, et grâce à une traduction logico-formelle de l'article "des" entrant dans la définition du nombre naturel, qui en précise la valeur arithmétique potentielle de "autant que vous voudrez", avoir produit l'infini en acte, ou même avoir donné à cet infini ses "conditions d'existence", ne peut logiquement être rien d'autre qu'un "exalté". Bref, on pourra résumer ces explications un peu longues, en admettant qu'il ne peut qu'être profitable à la bonne santé des mathématiques, que ses praticiens soient aussi capables, de temps en temps, de montrer des signes de bonne santé intellectuelle, dans d'autres domaines que les mathématiques. Car, ces considérations mises à part, notre travail aura plutôt tendu à montrer qu'une bonne partie de la théorie des ensembles pouvait être sauvée, et notamment, l'ensemble consistant de ce qui, dans cette théorie, (à l'élaboration de laquelle Cantor a apporté, comme tout un chacun, sa contribution d'ouvrier qualifié) était déductible de la théorie du gnomon et de la logique des tables de vérité, ensemble de possibilités mathématiques pures, dont l'"avenir" scientifique peut même apparaitre assez prometteur.
  

    

    

   

  Références :

  Gilles-Gaston Granger : Formes, opérations, objets, Vrin, 1994. La pensée de l'espace, Odile Jacob, 1999.

  Benjamin Barras : Les polyèdres réguliers, Scribd, internet.

  Emmanuel Kant : Critique de la raison pure, Garnier-Flammarion, 2006.

  Aristote : (sur Alcméon de Crotone) La métaphysique, Vrin, 1986. La physique, Vrin, 1999. Catégories, Vrin, 1976

  Pseudo-Archytas : Des catégories, Remacle. Org. (Internet)

  Platon : Timée, Epinomis, Remacle. Org. (internet)

  Philolaos : Fragments. Remacle. Org. (internet)

  Paolo Zellini : Gnomon, una indagine sul numero, Adelphi, 1999. Numero e logos, Adelphi, 2010.

  Jacques Chailley : L'imbroglio des modes, A. Leduc, 1977.

  Gustave Guillaume : Essai de mécanique intuitionnelle - espace et temps en pensée commune et dans les structures de langue, Presses de l'Université Laval-Québec, 2007. Temps et verbe, Honoré Champion, 1984.

    

   

    

   

    

    

  
  votre commentaire
   
•  

  3. Spirale de Théodore et polygone gnomonique de rang 4

  Par zalmoxis dans le 29 Août 2012 à 09:46

    

    

   SPIRALE DE THEODORE

  ET POLYGONE GNOMONIQUE DE RANG 4

    

    

    

  Le 27 août à 12h17, j'ai reçu sur le blog le message suivant de M. Axel Schneider. Si toutes ses remarques sont intéressantes, celle qui concerne la spirale de Théodore est d'ordre fondamental. En effet, la spirale de Théodore est tout simplement la structure duale du polygone gnomonique de rang 4.

  A. Schneider :

  Côté du carré de Vitruve / rayon cercle Vitruve = 8/5 unités (écart entre centre cerle et celui carré). Ce rapport est celui du flocon de Koch et 2 nombres de Fibonacci. Surtout on a 2 rectangles = le carré long de 3/4 et diagonale 5 et son complément de 4/1 et diagonale racine 17 (comme dans la spirale de Theodorus).
  
  5 et 17 : 1!+...+5!=1+...+17=153
  « Amis, leur dit-il, voulez-vous parier avec moi que je puis vous révéler à l’avance, le nombre exact des poissons que vous venez de capturer ? » Vie de Pythagore de Jamblique.
  
  E. Post avait pour ambition de trouver dans quelle mesure une théorie capable de formaliser l'arithmétique, partiellement récursive (ratio) pouvait être à la fois consistante et complète (mesure de l'incomplétude).
  
  Je pense comprendre pourquoi il évoquait le flocon de Koch avant de mourir avec Koch. C'est une question pythagoricienne et la solution est dans Vitruve.
  
  1531 suite Cunningham : J'ai besoin de vos connaissance sur le gnomon qu'i

  Le message de M. Schneider s'interrompt à cet endroit. 

   *

   

  LA SPIRALE DE THEODORE EST LA STRUCTURE DUALE DU POLYGONE GNOMONIQUE DE RANG 4.

   

  Spirale de Théodore

   

  Polygone gnomonique de rang 4. (On prend ici l'exemple du carré, mais tout ce qui s'applique ici au carré s'applique de la même manière au triangle gnomonique de rang 4).

  

   

  Le PG (polygone gnomonique) de rang 4 compte 16 blocs, la spirale de Théodore 16 blocs.
   
  Le PG de rang 4 est une structure qui permet de déployer les carrés des nombres entiers de 1 à 4, ces carrés se déployant dans l'intervalle compris entre 1 et 16.

  Symétriquement.
   
  La spirale permet de déployer les racines carrées des nombres entiers de 1 à 16. (La racine 17 ne doit pas être prise en compte dans l'analyse de la structure, puisque le bloc 16 doit être traité comme le 1, en les coordonnant par leur origine, comme on referme un éventail; la racine 17 n'est donc que le bord extérieur de la structure) - racines carrées des nombres  1 à 16 qui elles-mêmes, se déploient dans l'intervalle compris entre  1 et 4.

  La spirale de Théodore est donc une application immédiate de la clôture à quatre; elle n'est même qu'un redéploiement de la structure qui est celle du PG de rang 4. Cette structure vient donc s'ajouter à la liste de celles qui sont immédiatement déductibles des propriétés mathématiques de la tétractys.

  La spirale de Théodore est la structure duale du PG de rang 4, de la même manière que l'opération : "racine carrée de n" est l'opération duale de l'opération "carré de n".

  L'équation complète me paraît être la suivante : le polygone gnomonique de rang 4 est à l'égard des carrés des nombres 1 à 4, ce que la spirale de Théodore est à l'égard des racines carrées des nombres entiers, dont les solutions sont comprises entre 1 et 4. Soit, en généralisant :

  ST = D (PG).  (Où : ST : spirale de Théodore. PG : polygone gnomonique. D : "duale de ..." - dualité définie comme une application biunivoque sur l'ensemble des entiers.) 

  *

    

  Une autre remarque de M. Schneider est également des plus intéressantes : celle qui consiste à décomposer le carré gnomonique de rang 4 en 4 triangles rectangles : soit deux triangles de valeur (3-4-5) et deux autres de valeur (1-4-racine17).

   

  En effet ces deux triangles sont fondamentaux en ce que chacun d'eux correspond à un seuil de clôture.

  Le triangle (3-4-5) est le plus petit des triplets pythagoriciens.

  Le triangle (1-4-racine 17) est le plus grand des triangles de Théodore.

  Les valeurs des aires de ces quatre triangles sont respectivement de : 6, 6, 2 et 2, et le rapport du triangle de Théodore au triangle (3-4-5) est de 1/3, - rapport qui n'est autre que celui du gnomon (g/G = 1/3 ; où g : graine, et G : gnomon).

  * 

  A ce sujet, remarquons que les modernes (comme c'est déjà le cas de Platon dans son Théétète) sont incapables d'expliquer pourquoi Théodore s'est arrêté au 16 ème bloc. Ils continuent de penser que Théodore s'est arrêté là pour des raisons esthétiques, parce que l'ajout d'un 17 ème triangle aurait eu pour effet de recouvrir le début de la figure.

  En pythagorisme, ce qui se passe en deça de la clôture à 4 est fondamentalement différent de ce qui se passe après; et la clôture elle-même a le statut d'un seuil ou d'une coupure épistémologique. Seul ce qui se passe en deça de la clôture revêt une valeur axiomatique et fondamentale.

  Citons pour conclure le Théétète : "Théodore nous avait expliqué, avec les figures, quelque chose de ce qui concerne les puissances, nous faisant voir, à propos de celles de 3 pieds et de 5 pieds, que, en longueur, elles ne sont point commensurables avec celle de 1 pied, les prenant ainsi une à une jusqu'à celle de 17 pieds. Mais, je ne sais comment cela se fit, il s'arrêta à cette dernière." (Traduction de Léon Robin).* 

   *

  D'après ce que je comprends du message de M. Schneider, son sentiment personnel est que les divers éléments de ce dossier ont une importance de premier ordre, puisqu'ils pourraient permettre une résolution du problème d'E. Post qu'il nous résume en ces termes : montrer "dans quelle mesure une théorie capable de formaliser l'arithmétique partiellement récursive, pourrait être à la fois consistante et complète".

  Je lui souhaite bonne chance dans sa recherche.

    

  *17. C'est évidemment pour la même raison que le nombre 17 est, dans un polygone gnomonique de rang 4, le zéro logique de la relation additive, par application en miroir des huit premiers nombres sur les huit derniers (1+16 = 2+15 = 3+14 = ... = 8+9 = 17), et qu'il est, dans la spirale de Théodore, le bord, ou le zéro géométrique. Le nombre 17 correspond simplement, dans ces deux structures, au retour logique de la position zéro induit par la clôture de la tétractys, de la même manière que dans le système de notation décimal: - cette clôture se fondant, du reste, sur le même critère de "naturalité" que ce système même. 

    

    

  Guillaume DENOM

    

   

   

  
  votre commentaire