-
Par zalmoxis le 21 Août 2018 à 08:40
PENTAGONE ET HEXAGONE
Après tout ce que nous venons de dire, j'ajouterai encore un mot qui sera sûrement entendu de Nicandre. Le sixième jour du premier mois, lorsqu'on introduit la pythie dans le Prytanée , le premier des trois sorts qu'on jette pour vous est tiré sur le nombre cinq, d'abord trois, ensuite deux. La chose ne se fait-elle pas ainsi ? « Oui, répondit Nicandre, mais il est défendu d'en dire la raison aux étrangers. »
Plutarque
Pentagone et Hexagone
Si les nombres 2 et 3 sont les « principes » de la doctrine de la nature, en ce que par eux débute le récit de la genèse du monde, les nombres 5 et 6 forment la suite du même récit, en ce qu'ils exhibent les deux plus proches finalités auxquelles sont conduits ces deux principes.
2+3 = 5,
2x3 = 6.
Les nombres 5 et 6 peuvent donc être considérés comme les mariages des nombres 2 et 3, selon deux modalités distinctes ; (Charpentier qualifie les nombres 5 et 6 de « nombres conjonctifs »); toutefois, il semble qu'au nombre 5 seul convienne en propre le terme d'union. L'addition est la plus simple des unions, puisqu'elle absorbe deux termes en un seul, sans les faire disparaître. La seule chose qui a disparu étant précisément l'altérité, la séparation.
La distinction de ces modalités, pentagonale et hexagonale, constitue pour ainsi dire l'essentiel de la philosophie de la nature.
Fidèle à une tradition qui semble remonter à ..., Guénon associe le pentagone au microcosme et l'hexagone au macrocosme.
Il y a deux façons d'entendre les concepts de macrocosme et microcosme; soit comme la relation abstraite du "tout" à l'une de ses parties quelconques, soit comme un nouage qui a lieu en tout point de l'Univers, entre intériorité et extériorité d'une réalité quelconque. Seule la seconde de ces conceptions est pertinente pour ce qui nous concerne.
De ce point de vue toute monade à deux « cotés », deux « attaches » qui sont l'attache microcosmique à son plan propre, et l'attache macrocosmique à un plan supérieur.
Ainsi, le nouage qui, dans le Timée, associe les cercles du Même et de l'Autre aux plans respectifs de l'equateur et de l'écliptique, est parfaitement rigoureux ; il correspond au véritable nouage cosmologique de la terre (même si la distribution des termes « même » et « autre » peut être sujette à discussion) ; et conserve donc toute sa valeur, malgré l'obsolescence du modèle géocentrique auquel il donne lieu.
Seule cette acception à la fois locale et universelle des notions de microcosme et de macrocosme est pertinente pour le sujet qui nous concerne.
On peut donc, avec prudence, commencer par avancer que liaison ou l'association du pentagone et de l'hexagone a « quelque chose à voir » avec la constitution du cosmos. C'est en tout cas une idée récurrente dans la tradition pythagoricienne, où le couple formé par les nombres 5 et 6 se présente souvent comme un avatar, une reformulation du couple 2 et 3 du Lambda de Platon.
« Comme de l'Un, premier connu, rayonnent le cinq et le six... » (Dante, Paradiso)
Le contexte permettant d'identifier l'Un à Dieu, le 5 et le 6 sont présentés, dans ce vers, comme les deux premières réalités issues de l'Un, le degré de la « primauté » ayant reculé d'un degré, par rapport au Lambda de Platon. Guénon a montré que le nombre 11 avait, dans la comédie, une importance symbolique considérable (comparable à celle du nombre 9 de la vita nova) ; mais ce vers est le seul où nous est révélé quelque chose de la signification « génétique » de ce nombre.
Le traducteur André Pézard, habituellement très discret sur les aspects ésotériques de l'oeuvre de Dante, est convaincu que ce vers doit être interprété à la lumière de la géométrie, et livre une étonnante construction, dont on peut regretter qu'il ne l'ait pas commentée davantage.
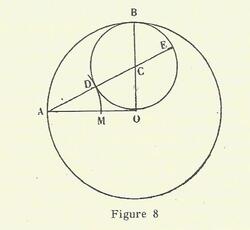
Il s'agit de construire, à partir d'un cercle et de son rayon, l'hexagone et le pentagone inscrits dans ce même cercle, en ne recourant qu'à la méthode euclidienne de la règle et du compas. Du pentagone est déduit le pentagramme étoilé.
Pézard identifie le cercle à l'Un-Dieu, et l'hexagone et le pentagramme, aux productions les plus immédiates du rayon de ce même cercle. Le rayon géométrique ayant clairement, ici, le sens symbolique de « rayonnement » divin.
La construction de Pézard nous semble faire écho à un dessin de Dürer, dans lequel le pentagone et l'hexagone sont construits avec la même contrainte euclidienne, non à partir du Cercle, mais à partir du double cercle du Vesica piscis.
Les deux constructions peuvent paraître complémentaires, la première affiliant le couple pentagone-hexagone à l'Un, la seconde, à la dualité première, dont le vesica piscis est le symbole. La première peut donc nous sembler relever de la métaphysique, tandis que la seconde relèverait plutôt de la cosmologie et de la science de la nature.
Remarque : Pézard est muet sur les sources qui l'ont inspiré, mais on peut remarquer que son dessin reproduit exactement une construction d'Arturo Reghini (ref).
Si de telles constructions peuvent être éloquentes sur la naturalité mathématique du nouage entre le pentagone et l'hexagone, elles sont malheureusement peu bavardes sur la différence qualitative entre ces deux figures. Si ces figures constituent un « couple » de la même nature que le couple pair-impair du lambda de platon, avec la même prétention à exprimer symboliquement le mariage, la hiérogamie de la création, de la nature universelle, alors, il doit exister entre ces deux figures des différences oppositives, dialectiques, aussi bien spécifiées que celles du couple Féminin-Masculin, qui est leur archétype.
Le nombre 6 est un nombre circulaire
Cette affirmation est associée à deux axiomes.
A. Le rayon d'un cercle est égal au côté de l'hexagone inscrit dans ce même cercle.
B. Si l'on empile autour d'un cercle des cercles de même diamètre, on constate qu'on peut disposer, en tout et pour tout, six cercles autour du premier, tous tangents entre eux et à ce cercle.
Ces principes mathématiques expliquent que, dans la plupart des traditions, le nombre 6 soit associé aux idées de cyclicité, de retour du Même, de bouclage... toutes idées qui nous conduisent au pôle de l'Identité, qui est le pôle « ternaire », le pôle « mâle » de la manifestation universelle.
A contrario, le nombre 5, comme ses « dérivés » géométriques les plus proches que sont le pentagone et le pentagramme étoilé, est associé au nombre d'or, lui-même considéré comme principe formel de la Vie, de la création, de la brisure de symétrie, ou encore de la non-périodicité... toutes indications qui pointent vers le pôle de l'Autre qui est, traditionnellement, considéré comme le pôle femelle de la manifestation universelle.
Ainsi pouvons-nous retrouver, dans les nombres 5 et 6, une résurgence des polarités sexuelles du Lambda, bien que ces distinctions n'y soient plus aussi nettes, et perdent une partie de leur pertinence, dans la mesure où chacun de ces nombres est déjà une combinaison de masculin et de féminin. En outre, cette résurgence est liée à une inversion des relations initiales entre sexe et parité, puisque le féminin y est, cette fois, associé à l'impair, et le masculin au pair.
Avant d'aller plus loin dans l'examen des réalités mathématiques, il sera utile de considérer ce que les traditions pythagoriciennes rapportent au sujet du nombre 5, et de ces figures associées que sont le pentagone et le pentagramme étoilé.
Les arcanes traditionnels du nombre 5 – le pentagramme Ugieia
Le pentagramme est considéré, selon la tradition, comme un signe de reconnaissance de la fraternité pythagoricienne.
Et, avant d'aller plus loin, on notera que, dans l'histoire du pythagorisme, la fonction du « signe reconnaissance » est associée à la création et à l'élaboration du concept de symbole, que nous utilisons toujours.
Et effet, le sumbolon, le symbole, était pour les pythagoriciens un signe de reconnaissance, qui consistait en une pièce de monnaie brisée à la séparation, en autant de morceaux que nécessaire, selon le nombres de frères. Le fragment conservé par chacun des frères le reliait, dès lors, physiquement, à l'instant de cette séparation, et lui était un gage infaillible sur l'authenticité de la retrouvaille. De même que seuls les vrais morceaux de la pièce originelle, auraient la possibilité de se rassembler, de même, seuls de vrais pythagoriciens, ou à défaut leurs représentants, pourraient être en possession de ces fragments de pièces. Le fragment, la partie, conservée par chacun des membres, porte en lui la marque du tout, de l'unité indivise constituée par la communauté des frères, selon une logique typiquement pythagoricienne à laquelle nous a longuement accoutumée la théorie du gnomon.
Les termes « signe de reconnaissance » et « symbole » sont donc investis, en pythagorisme, d'une charge particulière, due à cette synonymie partielle.
Un signe de reconnaissance doit nécessairement être un symbole, c'est à dire qu'il ne doit pas seulement « signaliser », « indiquer », (se réduire à la fonction du signe) mais incarner, produire lui-même la réalité dont il atteste ; et selon ce critère, il y a de bonnes raisons de penser que le pentagramme faisait office de « symbole suprême », ou de « symbole des symboles », d'un symbole capable de concentrer ou de conserver l'intégralité de la doctrine pythagoricienne.
La tâche essentielle du présent ouvrage sera de tenter de comprendre pourquoi.
Caractère liturgique
Le pentagramme était associé à un geste, un tracé rituel.
On relie par des segments 5 points de référence, correspondant à cinq parties du corps humain : nuque, épaules et hanches.
Par ce geste, il est indiquée que ces 5 parties du corps sont nouées, c'est à dire, liées, rassemblées, mais aussi tenues, dirigées.
Le pentagramme est un nœud.
On commence par la hanche gauche et l'on poursuit ainsi :
nuque, hanche droite, épaule gauche, épaule droite,
Pour finalement conclure en aboutant la corde du tracé :
hanche gauche.
Ce symbolisme possède, à l'évidence, un aspect « mortel » et un aspect « vital », inséparables l'un de l'autre, auxquelles correspondent dans la conception vulgaire les deux connotations, « maléfique » et « bénéfique » du pentagramme, mais qui, dans le contexte de la pensée traditionnelle, renvoie au « mythe » du démembrement de l'homme primordial : le « sacrifice » primordial d'un Dieu qui aurait été la condition de la création du monde, mythe dans l'esprit duquel, bien évidemment, mort et vie sont indissolublement liées..
Ce prétendu mythe n'est évidemment qu'un philosophème, qui veut que toute création soit, par définition, une division, et se nourrisse de la destruction d'une unité ontologique plus primordiale, d'une hénade, dans laquelle il est loisible à chaque tradition de reconnaître un de ses Dieux : qu'on l'appelle Osiris ou Dyonysos.
L'acte de la mise à mort, de sacrifice et de démembrement qui se déroule du côté divin coïncide, sans aucun reste, avec l'acte de création, de liaison protectrice et de vitalisation dont le « miracle » s'accomplit à chaque instant, de notre côté. Ce qui est assez montrer que la mort du Dieu n'est qu'apparente.
Comme les bris du sumbolon, les parties du corps du Dieu sont destinées (par la vertu même du rite) à se rassembler ; de sorte que la mort du Dieu ne contredit pas son immortalité, mais l'établit au contraire. Est immortel, non ce qui ne connaît pas la mort, mais ce qui la connaît au contraire assez intimement pour être capable de lui survivre : immortel est le dieu qui survit à sa propre mort.
Geste et tracé
C'est évidemment le côté bénéfique du symbole, celui qui gagne à la fin, qui est engagé dans le rituel pythagoricien, où ce geste, comparable au signe de croix des chrétiens, est synonyme de bénédiction et de salut. Et la vertu du geste se transportait, intacte, dans toute action de tracé, de dessin ou de gravure qui pouvait en conserver la teneur.
Traditionnellement, le dessin du pentagramme était légendé , dans chacune de ses branches, par les
5 lettres du mot UgiEIA qui signifie en grec « santé », et dont l'équivalent latin est « salus ».
Tout personne qui emploie aujourd'hui pour saluer le mot : « salut ! », ou pour bénir le mot « santé ! » renouvelle, sans le savoir, un usage pythagoricien.
Il convient, avant tout, de remarquer que ces termes nomment, dans l'antiquité, deux divinités de sexe féminin, l'une grecque, l'autre latine, qui sont dans leur panthéon respectif les déesses de la Santé, et que les théologies officielles ont donné pour « parèdre » ou pour « fille principale » (ce qui revient techniquement au même) soit au Dieu de la médecine Asclepios/Esculape, soit à Apollon, dont ce dieu médecin est souvent considéré comme le desservant, le substitut ou l'avatar.
En réalité, il est certain que ces déesses ont une histoire locale beaucoup plus ancienne, totalement indépendante des dieux masculins indo-européens qui leur ont été donnés pour époux. Les mots « Ugieia » et « Salus » ne sont pas des noms originaux, puisqu'ils ne sont que des qualificatifs exprimant des fonctions de la déesse. La seule tradition qui ait conservé une dénomination plus ancienne est la tradition celtique, où la déesse Santé se nomme « Sirona ». Comme ses pareilles latine et grecque, Sirona fut mariée à divers dieux gaulois ; mais son nom conserve le souvenir d'attributions beaucoup plus primitives, antérieures à ces refontes théologiques tardives, puisqu'il signifie – ô surprise – « grande étoile ». « Sir » est un radical signifiant « étoile » (une extraordinaire étude étymologique a d'ailleurs montré que les deux mots dérivaient d'une source commune), tandis que le suffixe « ôn » est un augmentatif signifiant « grand », présent dans divers noms de nombreux dieux celtiques tels que Maponos, etc. - Sans ce témoin celte, il serait impossible d'expliquer les caractères nettement stellaires, comme le diadème (très rares chez les divinités gauloises) dont se parent aussi les équivalentes latine et grecque, Salus et Ugieia.
Le tracé pythagoricien qui associe le nom de la déesse Ugieia à celui d'une étoile a donc bien le cartactère de restitution d'une donnée traditionnelle. A cette étoile mythologique correspondait, certainement, un astre du firmament, dont le souvenir n'a pas été conservé, mais pour lequel peuvent postuler plusieurs candidates : l'étoile polaire, Sirius, ou encore Vénus, avec pour cette dernière, cette coïncidence spectaculaire, que le tracé de sa révolution dans le ciel, correspond précisément à la figure d'un pentagramme.
Mais quelle qu'ait pu être cette étoile, l'essentiel est qu'elle ait été investie, pour notre monde, d'une fonction de bienfaisance, d'équilibre et de santé ; et donc, qu'elle représente pour ce même monde une forme d'ancrage, de stabilité, condition de son salut.
L'hypothèse d'une parenté étymologique entre notre déesse salutaire Sirona et Sirius n'a, en soi, rien d'invraisemblable; et Rémy Bayoud a même suggéré d'inclure dans ce procès les Sirènes de la tradition ésotérique pythagoricienne.
Ces créatures mythologiques jouent en effet un rôle des plus éminent dans la tradition secrète du pythagorisme. En liaison avec les points de la tétractys, elle représentent l'éternité, l'invariance, ou encore l'immutabilité qui préside aux transformations de la nature; et leur domaine d'élection est parfois désigné comme une "couronne", qui peut évoquer le "cercle" ou le "sphaïros", l'éther invariant qui enveloppe le cosmos empédocléen dans une pellicule d'éternité.
Par ce chemin, la déesse Sirona s'affranchit de la sphère étroitement médicale, pour s'élever au rang d'une déesse universelle, symbole de la condition, ou de la manifestation spatio-temporelle, et comparable à la déesse Isis.
De nombreux commentateurs ont remarqué la ressemblance entre les conceptions pythagoriciennes relatives à la santé et à la médecine, avec les conceptions taoïstes. Dans ces deux doctrines, la santé résulte d'un équilibre entre les deux pôles de la manifestation universelle : yang et yin, masculin et féminin.
Inversement, la maladie, le désordre, seront toujours la conséquence d'un déséquilibre entre ces deux pôles.
Si la création et la vie nécessite la participation et l'union de ces deux principes, la santé, la conservation de la vie, nécessitera, quant elle, un harmonieux équilibre, une juste proportion, une parfaite composition entre ces deux principes.
La tradition pythagoricienne attribue au nombre 5, entre autres qualifications, la propriété d'être un nombre nuptial, un nombre symbolisant le mariage, l'union.
On aperçoit par là que le pentagramme, dont la fonction est d'accomplir l'union, la médiation entre les nombres 2 et 3, représentant le féminin et le masculin, est réellement un symbole approprié à ce qu'il symbolise ici : la santé, elle même définie comme un harmonieux équilibre entre ces deux principes. Par cet aspect, le pentagramme peut être considéré comme un symbole « équivalent » au symbole chinois du yin-yang.
De la même manière qu'un certain équilibre est principe de Santé, un certain équilibre est principe de Justice. Souvenons-nous que la racine LeG-s, justice, est apparentée aux racines LoGos, LiGere, exprimant l'idée de lien.
Aristote définit le principe de la justice au moyen des médiétés pythagoriciennes.
Nos traditions occidentales montrent une confusion assez fréquente des symboles de la justice, comme celui de la balance, avec ceux de la médecine et de la pharmacie. Et Charpentier remarque à ce sujet :
« La notion de Justice est pour les Pythagoriciens plus large que pour nous : elle désigne l'harmonie unissant l'Homme au Cosmos entier en un accord parfait, auquel conviendrait d'ailleurs mieux le nom de justesse. »
Sans perdre les caractères originaux issus de ses origines pythagoriciennes, le symbolisme du pentagramme s'est conservé à travers toute l'histoire de l'ésotérisme chrétien, jusqu'à la franc-maçonnerie, dont l'étoile flamboyante est un des symboles majeurs.
Après cet aperçu des données traditionnelles relatives au pentagramme, il nous sera possible d'aller un peu plus loin dans l'examen des réalités mathématiques.
Dans un premier temps, on examinera les très nombreuses relations qui existent entre le nombre 5 et le nombre d'or.
En second lieu, on approfondira la relation particulière qui existe entre le nombre d'or et la notion d'équilibre, relation qui éclaire, non seulement, le symbolisme du pentagramme et l'association de cette figure aux idées de Santé et de Justice, mais aussi, le fait que le nombre d'or ait toujours été crédité d'un potentiel de signification « physique » et cosmologique, qu'il passe pour un nombre apte à représenter l'équilibre des forces universelles.
Si les nombres 5 et 6 peuvent tous deux être considérés comme des « mariages » des nombres 2 et 3, il semble qu'au nombre 5 seulement correspondent l'idée d'union. L'addition est une image parfaite de l'union de deux termes, en ce qu'elle ne supprime, de ces termes, absolument rien d'autre que la séparation, la dualité, en les réunissant en un seul.
Et comme on a vu que, dans le lambda, la procession hors de l'un prend appui sur une dualité, (formée des 2 premières réalités issues de lui). On va voir que, dans le nombre d'or, la procession s'appuie sur une biunité, une dualité « réunifiée » (matérialisée par le nombre 5) ; de sorte que là où on avait une procession duale, on a maintenant une procession directe. D'autres arguments viendront étayer cette thèse que le nombre d'or représente, justement, ce principe de procession directe, avec cette précision technique de « la plus directe ».
Remarque incidente le pentagone.
Cette propriété « processionnelle » du nombre d'or peut être rapprochée d'une propriété mathématique spécifique du pentagone.
Maël Mathieu, qui reconnaît dans le pentagramme un symbole de "l'homme transcendant", remarque au sujet du pentagone :
La propriété géométrique essentielle et fondamentale de tout pentagone, qui explique (du moins en partie) son importance symbolique, est qu'il est toujours inscrit et circonscrit à une certaine conique et détermine univoquement ces deux coniques ; il est le seul polygone à posséder cette propriété. Or une conique, qui est l'équivalent projectif d'un cercle, est un symbole de la totalité manifestée. Le fait que le pentagone détermine univoquement sa conique circonscrite s'interprète donc comme : l'Homme transcendant détermine univoquement la totalité manifestée dont il est le centre. On remarquera à ce propos que le nombre cinq est le symbole traditionnel de l'Esprit.
Il semble bien exister un rapport analogique entre la conique comme forme, et les principes de procession et de conversion qui sont les fonctions de l'hénade.
Mael Mathieu remarque que chez Proclus, les notions de Procession et Conversion sont complétées par un troisième terme, la Manence, qui est en quelque manière la synthèse des deux premières, tout en formant une instance indépendante, et un "moment" dialectique, qui domine en alternance avec les autres. Il note :
Ces trois "moments" sont à la fois unis et hiérarchisés, mais selon un ordre circulaire ; chacun d'eux est compris dans les deux autres, et a préséance sur eux sous un certain rapport.
Quant à la manence :
Il y a en elle un double aspect, qui peut être vue comme la synthèse finale de la procession et de la conversion, mais qui peut aussi précéder celles-ci d'une manière radicale et absolue. Et il y a aussi un double aspect dans la conversion, qui peut être vue comme le moment ultime de la procession, mais aussi comme sa condition, car seul ce qui est susceptible de se convertir - c'est-à-dire de faire retour au Principe - peut procéder.
Chez Proclus, le concept de manence est intimement lié à celui de l'Éternité comme dénomination du Principe suprême.
De fait, quelle peut bien être cette instance de "synthèse" entre les fonctions de procession et de conversion, sinon ce qui réalise entre elle un équilibre per-manent, un équilibre qui se maintient à travers l'alternance des trois principes?
L'autonomie « ontologique » du pentagone, sa capacité autonome de procession, semble devoir être rapproché de la capacité du nombre d'or, de réaliser, justement, la procession géométrique « la plus directe ».
En outre, le nombre d'or comme le pentagone, par cette parenté intime avec le principe procession lié au développement d'une conique, peuvent tout deux être rapprochés de la fonction de l'Hénade.
Mais commençons par rappeler succintement les rapports entre nombre 5, pentagone et nombre d'or.
Nombre 5 et nombre d'Or
L'équation du nombre d'or s'écrit de nos jours conventionnellement :
x = (√5+1)/2
Et il existe bien d'autres définitions de phi faisant apparaître le nombre 5, dont celles-ci, relevées par l'auteur du site Harpakheredblog :
Φ = 5 ^ 0,5 x 0,5 + 0,5
Φ= √(( 5+√5) / (5-√5))
Phi = e ^ asinh(0,5)
Φ=2 cos (Π/5)
Dans l'antiquité, le nombre d'or était conçu comme un problème géométrique relevant de la théorie des proportions, dans lequel il s'agit de diviser un segment en deux portions, de façon à ce que « la plus petite portion soit à l'égard de la plus grande, comme la plus grande est à l'égard du tout. »
On a :
c/b = b/a = Φ
mais aussi
a+b = c
expression dont on sait qu'elle régit la suite de Fibonacci, et dont on peut déjà remarquer qu'elle correspond à une algébrisation de la relation entre les trois premiers nombres du Lambda, qui occupent le sommet de la figure
1+2 = 3
Dans le pentagramme, ce rapport apparaît entre le côté du pentagone intérieur, et celui d'une branche quelconque de l'étoile, chaque branche formant un « triangle d'or » aïgu, triangle isocèle dont les côtés inégaux sont dans le rapport phi.
Deux autre triangles d'or, de tailles supérieures, peuvent être obtenus en prenant successivement pour base du grand côté les segments : a+b, puis b+a+b ; cet enchevêtrement de triangles d'or étant le principe générateur des pavages de Penrose.
Après cet aperçu très rapide des relations entre le nombre 5, le pentagone et le nombre d'or, il est temps d'introduire un énoncé de science commune dont nous empruntons la forme à Schwaller de Lubicz :
Le nombre d'or est le principe naturel des lois de l'équilibre.
Du point de vue cosmologique, les lois de l'équilibre sont celles qui garantissent la cohésion de l'univers à travers toutes ses transformations, mais aussi, le contraignent à demeurer toujours égal au quantum « 1 ».
Charpentier, qui reconnaît également dans le nombre d'or une expression mathématique du principe d'équilibre, invoque pour l'occasion un principe métaphysique supérieur, qu'il emprunte à Guénon, et qu'il érige au rang d'axiome de science pythagoricienne:
« L'équilibre est le reflet dans l'existence de l'immutabilité du principe ».
Autrement dit, l'équilibre des forces cosmiques n'est rien d'autre que la traduction de la présence et de l'action de l'Un, à travers tout le cycle de l'Existence et de la manifestation universelle.
La question qui se pose à nous est : en quoi le nombre d'or est il particulièrement approprié à l'expression des lois de l'équilibre. C'est le fil que l'on suivra par la suite en passant en revue différentes approches du nombre d'or.
le nombre d'or par la théorie des médiétés
La proportion dorée est la seule proportion qui satisfasse à la fois la médiété Nicomaque 2 dite "géométrique", telle que :
pour trois termes consécutifs :
a<b<c
On a :
(b-a)/(c-b) = a/b = b/c
médiété dans laquelle :
ac = b2
(Exemples de cette médiété les proportions "double" (1,2,4,8...) ou "triple" (1,3,9,27...) qui correspondent respectivement aux jambes gauche et droite du lambda de Platon.)
Et la médiété Nicomaque 10 (de Fibonacci), telle que, pour trois termes consécutifs : a<b<c, on a :
(c-b) / (c-a) = a/b
médiété dans laquelle :
a+b = c
Exemple de cette médiété la suite de Fibonacci (0,1,1,2,3,5,8...)
Autrement dit : la proportion dorée est la seule proportion "de Fibonacci" qui soit géométrique, et inversement.
Ou plus exactement : en posant c/b = x et en égalant les médiétés N2 et N10, on retrouve l'équation x*x = x + 1 dont une des solutions est la proportion dorée.
Exemple de proportion dorée, dans laquelle chaque terme est le phi-uple de son prédécesseur, définie à partir de l'unité "1" :
( 1, phi, phi2,...)
La proportion dorée est ainsi définie comme unique intersection de 2 ensembles bien définis, dont chacun est l'ensemble des solutions d'une médiété à 3 termes de Nicomaque – en l'occurrence les médiétés 2 et 10.
De la même manière que, dans le Lambda, l'unité originaire correspond au croisement de deux progressions géométriques, l'une double, l'autre triple, de même, la proportion dorée correspond au croisement de deux médiétés : « géométrique » et de « Fibonacci . Nous allons voir que la plupart des approches du nombre d'or insistent particulièrement sur son rapport avec l'une de ces deux médiétés, au détriment parfois de l'autre ; et de fait, elle peut être obtenu à partir de chacune d'elles par saturation interne, sans le truchement de l'autre. Mais ici, on doit précisément avoir égard au fait que la proportion dorée représente un cas-limite pour les deux à la fois ; autrement dit que, pour chacune d'elles, elle incarne la présence du « même » dans un ensemble « autre »... cette dernière formulation devant faire sentir qu'elle répond au critère qu'une médiété doit posséder, pour être, selon le mot de Proclus, « ce plus puissant des liens » qui est le lien d'amour, que l'on peut schématiser par le fait, pour un être donné, d'avoir dans un autre être sa « raison d'être ».
(Intégrer quelque part : Chaîne d'or des orphiques et lien d'amour. Dernier vers des buccoliques lu par Charpentier
Omnia vincit amor, et nos cedamus.
Vincit est une forme verbale commune à deux verbes différents : « vincere », vaincre, et « vincire », lier ; Virgile joue sur cette ambivalence pour transmettre un enseignement qui est le même que celui du dernier ver de la comédie de Dante.)
Remarquons maintenant que la structure du Lambda possède pour nous des applications nouvelles, d'une généralité mathématique supérieure à celle qu'on lui connaît par l'exegèse du Timée.
Lambda de Platon
1 origine commune
2 3 départs des médiétés géométriques « double » et « triple »
Lambda de Proclus
Médiété géométrique
Médiété arithmétique Médiété harmonique
(autre) (même)
Lambda d'Or
Proportion dorée (solution commune)
Médiété de Fibonacci Médiété géométrique
(ensemble des suites de F) (ensemble des suites géométriques)
Charpentier et Reghini.
Charpentier : « Pourquoi le pentagone est-il signe de vie ? Comme d'autres polygones, il peut se présenter sous deux formes ; il est soit convexe, soit étoilé... Et ces deux formes sont le résultat d'une alternance...
« En effet, l'étoile, une fois engendrée par les diagonales du pentagone convexe, contient maintenant en son centre un nouveau pentagone convexe, d'orientation inverse et plus petit en quantité de surface que le premier, mais tout semblable à lui par la forme, qui manifeste une qualité inchangée. En effet chacun de ces pentagones est en relation dorée avec tous les autres, ce qui garantit le maintien de sa qualité à travers tous les changements quantitatifs.
Cette alternance que les géomètres qualifient de « pulsante » est « le meilleur modèle de tous les rythmes vitaux ». Quant à « la loi qui rend possible cette alternance géométrique, c'est la même qui s'étend à tout le domaine de l'Existence, et qu'on a nommé « Nombre d'or » ou « divine proportion ».
Charpentier remarque que, à l'image de la doctrine pythagoricienne, ce nombre a donné lieu à d'innombrables commentaires, sans que personne ait su dire de quoi il s'agit en fait.
La réponse passe par cette question :
« De quoi a besoin, pour rester en vie, une créature quelconque ? La réponse consiste en cette double condition : 1. Elle doit garder la forme qui répond à sa définition, sous peine de devenir « autre chose », en perdant son identité. 2. Mais il faut qu'elle garde, en même temps, la possibilité de se développer, c'est à dire de changer, en devenant « relativement autre ».
Nous retrouvons donc ici les éléments caractéristiques de la dialectique du Timée.
Charpentier remarque que la suite de Fibonacci (1, 1, 2, 3, 5, 8...), dans laquelle chaque terme est la somme des deux qui le précèdent, et qui est associée à la croissance « en spirale » de nombreuses formes naturelles : végétaux, coquillages, nébuleuses, manifeste précisément cette capacité à « maintenir une forme constante » à travers des états variables, son principe régulateur étant précisément la proportion dorée vers laquelle tend la suite de Fibonacci.
Selon cette approche c'est donc la relation algébrique : a+b = c, caractéristique de la suite de Fibonacci, qui expliquerait l'universalité physique et cosmologique de la proportion dorée.
Cette explication est assurément séduisante, à un détail près : elle omet que la proportion dorée est une proportion géométrique stricte, qualité que ne peut posséder aucune suite de type « Fibonacci », hormis celle qui a exactement pour matrice le nombre d'or, et qui constitue un cas limite.
Charpentier estime, apparemment, qu'il est propre au principe des suites de Fibonacci de ne pouvoir produire qu'une approximation de plus en plus serrée du nombre d'or ; ce que l'on peut lui contester. En effet, si le principe de ces suites est défini de façon purement algébrique, comme dans la théorie des médiétés, alors, rien n'interdit de considérer la suite exacte du nombre d'or (1, phi, phi carré, …) comme un cas particulier de la médiété Nicomaque 10 (« de Fibonacci »), au même titre exactement que la suite (1,1, 2, 3, 5,...).
Rappelons que la médiété Nicomaque 10 est une relation entre 3 termes a<b<c telle que
(c-b)/(c-a) = a/b
Or les deux suites susmentionnées satisfont bien cette condition.
Charpentier, qui n'envisage pas cette éventualité, estime en conséquence que, pour obtenir une expression plus exacte du nombre d'or, il faut quitter le terrain de l'arithmétique, et emprunter celui de la géométrie.
Pour ce faire, il recourt au théorème de Pythagore.
L'hypoténuse d'un triangle rectangle de cathètes 1 et 2 vaut racine de 5.
Si l'on rabat l'hypoténuse de valeur racine de 5 sur le même axe que le côté de valeur 1, on obtient un segment de valeur 1 + racine de 5, segment qui, divisé en deux (dans le contexte antique de la « corde à noeuds » cette opération peut se faire en repliant une fois sur elle-même la « corde » en question), on obtient un segment qui se trouve, à l'égard du côté de valeur 1, dans le rapport « phiuple », autrement dit : un segment de longueur phi.
Par une voie plus directe, Reghini parvient à une conclusion assez semblable. Sa définition de la proportion dorée, d'un synthétisme remarquable, ne met en jeu que la proportion géométrique, et sa propriété principale ac = b2 :
On appelle section dorée d'un segment ou « section divine » cette partie du segment telle que le carré qui a ce segment pour côté équivaut au rectangle qui a pour côtés tout le segment et la partie restante.
(...)
Symétriquement à la définition qui qualifiait la proportion dorée de « seule proportion de Fibonacci qui soit aussi géométrique », on définit maintenant la proportion dorée comme « la seule proportion géométrique dans laquelle le troisième segment est égal à la somme des deux premiers »). Dans toutes les autres proportions géométriques, sans exception (inclus évidemment les proportions « double » et « triple » du lambda), le troisième segment ne peut pas être égal à la somme des deux qui le précèdent.
La proportion dorée représente donc, à cet égard, une forme « épurée » du principe de progression géométrique, résultant d'un NOUAGE INTERNE.
Si l'on admet que la médiété géométrique est en charge du principe de procession, la proportion dorée n'est pas autre chose qu'une médiété géométrique « réfléchie en elle-même ».
Là où le Lambda représente une procession « duale », procession parallèle du pair et de l'impair, la proportion dorée représente en quelque sorte un principe de procession « directe » ou de procession « tout court ».
Si l'on s'avise maintenant de traduire la définition de Reghini, définition géométrique reposant sur le rapport entre longueurs de segments, en termes arithmétiques, on obtient l'équation :
1/phi x phi = 1 carré = 1
Et cette équation nous rappelle immédiatement un axiome arithmétique des plus triviaux, qui veut que « le produit d'un nombre et de son inverse soit toujours égal à 1 ». Et c'est de cette manière, certainement, que la proportion dorée peut être définie de la manière la plus profonde : COMME UNE TAUTOLOGIE DIRECTEMENT EXPRIMEE DU NOMBRE UN, ou encore, comme le « ratio » minimal, ou « ratio de ratio », uniquement générateur du nombre 1.
C'est cet aspect absolument RADICAL qui explique que, sur le plan de la réalité physique, la proportion dorée soit le ratio le plus propre à exprimer l'EQUILIBRE, notion dont a déjà vue qu'elle devait elle-même être définie comme la « conservation », la « permanence » ou le « reflet » de l'Un.
Derrière ces deux approches de la proportion dorée par Charpentier et Reghini se profile le triangle rectangle (1,2, racine 5), et à sa suite, le triangle isiaque (3,4,5), dont nous avons montré ailleurs la complémentarité et les liens ; de sorte que le problème de la proportion dorée se trouve désormais placé sous le signe du théorème de Pythagore. C'est cette approche très importante, et riche, dont nous essaierons maintenant de développer quelques aspects particuliers.
-
Par zalmoxis le 21 Août 2018 à 08:41
LA TRADITION DU NOMBRE 515 :
DANTE, DÜRER, JORGE ALFONSO
Au 33e chant de son purgatoire, Dante place dans la bouche de Béatrice la prophétie suivante :
« car je vois à coup sûr – et si, l'annonce -
tels astres, francs d'achoppail et encombre,
proches déjà de nous donner bon temps,
où mû par Dieu un cinq cent dix et cinq
viendra occire enfin la larronnesse
et le géant qui fornique avec elle. »
Cette prophétie conclut un long récit symbolique commencé au chant 32, où Dante, conduit par Béatrice et plongé dans un état léthargique, est saisi d'une série de visions touchant le destin de l'église, et sa lutte avec la puissance temporelle de l'Empire.
La prophétie reprend, en la précisant, une prédiction formulée par Virgile dès le premier chant de l'enfer, qui donne d'autres indications sur la nature de cet « envoyé de Dieu » auquel s'identifie le 515.
Harcelé par une Louve, symbole traditionnel de l'avarice qui, dans la comédie, symbolise la Rome des papes, cause des malheurs du poète, Dante demande protection à Virgile contre les assauts de cette bête, et ce dernier lui répond :
… cette bête ici, pour quoi tu cries,
ne laisse homme passer par ses chemins,
mais si fort le guerroie qu'elle le tue ;
et sa nature est si mauvaise et felle
que jamais ne s'emplit sa convoitise,
et repue elle a faim plus que devant.
A vingt et trente mâles elle s'accouple ;
ains, plus seront, tant que vienne le Vautre
qui la fera mourir à grand douleur.
Cil ne paîtra ni terraile ni peautre,
mais sapience et amour et vertu,
et sera né entremi fautre et fautre.
De l'humble Ytaille il sera le salut
pour qui mourut Camille la pucelle,
Nisus, Turnus et Euryal navrés.
Cestui la chassera par toute ville
atant qu'il l'ait remise dans l'enfer
là d'où Envie jadis la débûcha. »
Avant même que cette hypothèse ne soit confirmée par un examen du texte de Dante, le nombre 515 associé à la figure du l'envoyé de Dieu, a été rapproché du nombre 666, qui dans l'apocalypse, désigne la « bête », annonciatrice du règne de l'antéchrist. Et de fait, toute la vision du chant 32 du purgatoire apparaît comme une reprise, ou comme un prolongement de la prophétie Johannique.
Dans la vision de Dante, le char de l'église, d'abord conduit par Béatrice (représentant ici la grâce divine), est attaché à un arbre - qui fleurit - avant de subir les assauts d'un aigle, d'un renard et d'un dragon. L'aigle représente la puissance impériale. En attaquant le char, l'aigle lui laisse « des plumes » de sa puissance ; le char se transforme en un monstrueux char-à-plumes ; une putain et un géant en prennent possession et l'emportent.
Cette vision semble calquée sur l'apocalypse où, comme l'a remarqué Auberlen, la femme du chapitre 12, symbole de l'Eglise, reparaît au chapitre 17 comme prostituée, parce que l'Eglise est devenue infidèle à son Epoux en s'alliant au pouvoir civil.
Et de même manière que l'arrière plan historique de l'apocalypse concerne, très généralement, la persécution des chrétiens et l'annonce, à vocation consolatrice, de la chute et de la destruction de l'Empire romain, la vision du chant 32 du purgatoire narre les tribulations de l'Eglise confrontée à l'empire romain-germanique, auxquelles doit mettre fin la venue du Lévrier justicier « envoyé de Dieu ».
Ces parallèles assez transparents en eux-mêmes, ont été confirmés de manière éclatante par les recherches philologiques de Rodolfo Benini, qui remarque :
« Dante a imaginé de régler les intervalles entre les prophéties et autres traits saillants du poème, de manière que ceux-ci se répondissent l'un à l'autre après des nombres déterminés de vers, choisis naturellement parmi les nombres symboliques. (…) Et voici apparaître les fameux 515 et 666 dont la trilogie est pleine: 666 vers séparent la prophétie de Ciacco de celle de Virgile, 515 la prophétie de Farinata de celle de Ciacco ; 666 s'interposent de nouveau entre la prophétie de Brunet Latin et celle de Farinata, et encore 515 entre la prophétie de Nicolas III et celle de messire Brunet. »
On retiendra de ces remarques que le nombre 515 se présente comme opposant bénéfique au nombre maléfique 666 ; l'alternance de ces nombres dans le poème pouvant symboliser le déroulement d'une lutte apocalyptique dans laquelle les deux principes dominent à tour de rôle, jusqu'à la victoire finale du principe du bien.
Mais avant d'aller plus loin dans l'examen des prophéties de Dante et du mystérieux élu qui en est l'objet, il sera bon de revenir au texte de l'Apocalypse, qui est sa principale source d'inspiration.
La bête de l'Apocalypse
On omet souvent de remarquer que, dans l'Apocalypse, la venue de la Bête est saluée comme un événement favorable, qui doit permettre la survenue d'un événement heureux. Les deux événements sont liés dans les versets 9 et 10 du chapitre XII.
9 Il a été jeté le grand dragon, l'antique serpent qu'on appelle le diable et le Satan, lui qui égare tout le séjour, il a été jeté sur la terre et ses anges ont été jetés avec lui.
10 Et j'ai entendu une grande voix dans le ciel, elle disait : C'est maintenant le salut, la puissance et le règne de notre Dieu et le pouvoir de son Christ, car il a été jeté l'accusateur de vos frères qui les accusait jour et nuit devant notre Dieu.
De la même manière exactement, la révélation du « chiffre de la bête » au dernier verset du chapitre XIII, est immédiatement suivi par la vision de l'Agneau debout sur le mont Sion au premier verset du chapitre XIV :
XIII, 18 Ici est la sagesse : Que l'intelligent calcule le chiffre de la bête car c'est un chiffre d'homme et ce chiffre est six cent soixante-six.
XIV, 1 Et j'ai vu, et voici l'agneau debout sur le mont Sion et avec lui cent quarante-quatre mille qui ont son nom et le nom de son Père écrits sur leur front.
Non seulement le parallélisme est confirmé entre la venue de la bête et l'établissement du règne du Christ, mais le nombre maléfique 666 se voit clairement opposé un nombre « bénéfique » : les 144 « myriades » qui composent l'armée des élus du Christ.
Le nombre 144 est considéré comme symbolisant la plénitude, en ce qu'il est le carré de 12
144 = 12 x 12
Le nombre 12 se réfère aux 12 tribus d'Israël dont sont extraits les élus ; mais il peut aussi se référer aux 12 apôtres du Christ. Le produit 12 x 12 pouvant dès lors exprimer l'union de l'ancien et du nouveau testament, et l'accomplissement complet de la prophétie.
Sur le plan mathématique, on peut remarquer que 144 est également le 12ème nombre de Fibonacci.
Il peut donc être représenté comme le sommet d'un lambda à 12 étages, dont les jambes seraient respectivement formés par la série des nombres carrés, et celle des nombres de Fibonacci.
Cette remarque prendra tout son intérêt plus loin, lorsque nous aurons à évoquer le nombre 55.
Mais en attendant, on peut remarquer que le nombre 144 peut s'exprimer de la manière suivante :
(6 + 6) x (6 + 6)
Sous cette forme, on admettra que ce nombre bénéfique présente un troublant air de ressemblance avec le nombre « maléfique » qui est celui de la bête. Les deux nombres semblent plutôt des complémentaires, exprimant l'un comme l'autre l'alignement des planètes, ou la complétude des temps. Le second nombre étant le correspondant « dans l'ordre supérieur » (L'agneau debout sur le mont Sion, représentant symboliquement « le point le plus élevé de la terre ») de l'événement advenu dans l'ordre inférieur (le serpent jeté « sur la terre »).
Nombre des élus (6 + 6) x (6 + 6)
Nombre de la bête 6 6 6
Mais nous allons voir à présent que cette apparence de complémentarité sur le plan symbolique peut être doublée par une réelle complémentarité mathématique, extrêmement précise et signifiante.
On a remarqué en d'autres occasions que les nombres palindromes pouvaient être vus comme des exemples particuliers d'une fonction palindromique plus générale, qui concerne elle « toute formule arithmétique qui demeure inchangée pour une rotation de 180 degrés sur elle même », ou encore, qui possède dans sa structure la symétrie du miroir.
De cette manière, un nombre palindrome peut être envisagé comme un « formulaire » qui peut être décliné de plusieurs manières, autres que le seul agencement décimal des chiffres arabes ; la formule 666 pouvant par exemple être interpretée comme :
6 + 6 + 6
ou
6 x 6 x 6
En adoptant pour le texte de l'Apocalypse cette dernière option, la complémentarité du nombre de la Bête et du nombre de l'Agneau devient beaucoup plus bavarde.
En effet 6 x 6 x 6 = 216
Nombre dont on a vu qu'il correspondait au cycle des réincarnations de Pyhagore, d'une part, mais aussi au développement gnomonique tridimensionnel des trois cubes adjacents au triangle Isiaque, formule qui correspond à un développement externe des équations de Pythagore où d'une part
33 + 43 = 53
mais en outre :
33 + 43 + 53 = 63 = 216
En adoptant pour nombre de la bête le nombre 216, on remarque immédiatement que :
216 + 144 = 360
Les nombres 144 et 216 deviennent ainsi des valeurs angulaires, et le nombre 216 correspond très exactement à « ce qui manque à l'angle 144, pour compléter le cercle 360 ».
Si l'on définit dans un cerle, à partir de son centre, un angle dont les mesures, intérieure et extérieure, sont égales à 144 et 216 degrés, on obtient une division de la circonférence selon le rapport 2/3, à partir de laquelle il est aisé, en comblant les intervalles, de retrouver les trois sommets complémentaires du pentagone régulier. Ces trois sommets complémentaires, reliés entre eux, forment un triangle d'or aigu.
Ces valeurs angulaires 144 et 216 sont d'ailleurs loin d'être des inconnues, puisqu'on dérive d'elles toute la symétrie du pentagone, comme celle du nombre d'or et des pavages de Penrose.
On les retrouve en particulier dans le rhombe de penrose, qui est un losange d'or décomposable en 2 pièces, la paire « kite and dart » (fléchette cerf-volant) permettant de construire de nombreux pavages de Penrose, ou encore en 4 pièces – fléchette et cerf-volant se décomposant à leur tout en 4 petits triangles d'or, aigu et obtus.
Poursuivons.
Le rapport 144 / 216 est égal au rapport 2/3. Autrement dit, au rapport générateur du Lambda de Platon, qui met en relation « les deux premières réalités issues de l'un ». Aussi étrange que cela puisse paraître, la lutte de la Bête et de l'Agneau apparaît ainsi comme un renouvellement de la hiérogamie de la création.
Poursuivons.
Dans l'apocalypse, les 144 000 élus sont encadrés par 4 animaux qui tout au long de l'Apocalypse, symbolisent « Les 4 directions, les 4 vents, etc » Autrement dit le partage d'une aire quelconque en quatre quartiers divisionnaires. Cette image suggère immédiatement de diviser en 4 la procession des élus.
144 / 4 = 36
Les élus se répartissent donc en 4 cohortes, dont chacune correspond à une division décimale du cercle 360.
Si l'on assimile la plénitude du cercle 360 à la plénitude de la tétractys, alors, le nombre 144, nombre de l'Agneau, peut être associé au trépied de la tétractys, qui est pour ainsi dire sa colonne vertébrale, son axe majeur, et le nombre 216, nombre de la bête, à l'hexagone tournant autour de ce trépied.
Dans cette tétractys, tout est hexagonal au premier regard. La répartition des points du plan est hexagonal, et les valeurs des éléments (36) et du tout (360) empruntées au système sexagésimal.
Cependant le rapport numérique entre les deux éléments constituants, trépied et hexagone, 4/6 (égal à 2/3), est lui, comme on l'a vu, virtuellement pentagonal. On a là une illustration particulièrement importante d'un principe qu'on rencontre ailleurs sous d'autres formes est qui peut s'énoncer « la présence du pentagonal au cœur de l'hexagonal ».
On remarque que le rapport 2/3 est omniprésent dans les pavages de Penrose dont il est un trait caractéristique. Exemples, le rhombe de Penrose constitué de 4 obtus, 6 aigus (qui est un analogue strict de la répartitition trépied hexagone de la tétractys) ou encore cette très belle construction appelée « soleil », composée de 100 pièces : 60 kites et 40 darts.
On remarque enfin que les Nombres 144, 216 et 360 sont tous multiples de 9. Donc, en plus d'induire la division du cercle 360 en 5 parties, correspondant aux sommets d'un pentagone, ils sont placés sous la puissance « unificatrice » du nombre 9 (associée à la conservation de l'unité dans les multiples), ce qui les rend apte a exprimer les caractères généraux de la condition spatio-temporelle.
On voit bien que, dans cette conception le drame historique de l'apocalypse n'est qu'un prolongement du drame de la nature. Son déroulement est régi par les mêmes nombres, les mêmes figures et les mêmes lois.
Les autres nombres clés de la Comédie
Selon Benini, il y aurait pour Dante trois couples de nombres ayant une valeur symbolique par excellence : ce sont 3 et 9, 7 et 22, 515 et 666.
René Guénon tombe d'accord avec analyse, et ne s'en écarte que pour le nombre 22, qui ne lui semble important qu'en tant que multiple du nombre 11, plus essentiel, et dont d'autres multiples (33 et 99) jouent dans l'oeuvre un rôle tout aussi important que le nombre 22.
Même si nous suivons Guénon, on peut remarquer en faveur de Benini que le nombre 22 s'inscrit dans la droite ligne de la tradition apocalyptique, les 22 chapitres de l'Apocalypse n'étant pas plus arbitraires que les 99 chants de la comédie ; d'autant plus que (cette fois-ci en faveur de Guénon), l'oeuvre comporte une division binaire nettement marquée, qui fait apparaître, dans son plan en 22 chapitres, une division 11+11. Ces 22 chapîtres pouvant, bien évidemment, être rapprochés des 22 lettres de l'alphabet hébreu...
Mais revenons à Guénon qui précise :
La vérité, c'est que le nombre 11 jouait un rôle considérable dans le symbolisme de certaines organisations initiatiques... En dehors des significations diverses qui peuvent s'attacher à lui, l'emploi qu'en fait Dante constituait un véritable « signe de reconnaissance », au sens le plus strict de cette expression.
Il est aujourd'hui accepté que Dante était rattaché à diverses organisations initiatiques de filiation templières, comme la fede santa et les fidèles d'amour, dans lesquelles le nombre 11, comme le pentagramme, constituait un signe de reconnaissance.
Approches du nombre 515 : les nombres 11 et 55
11
Si nous nous arrêtons au nombre 11, c'est qu'il constitue la clé d'une première lecture du nombre 515, fondée sur l'addition de ses éléments constituants.
5+1+5 = 11
Dans cette interprétation, la dizaine formée par les nombres 5+5 peut être assimilée aux 10 points de la tétractys, ou encore aux 10 sephirot, tandis que le nombre 1 situé au milieu (correspondant lui aussi à une dizaine), peut être assimilée, à la onzième sephira, ou encore au « tout » de la tétractys, à la totalité unitaire et indivise dont ses parties procèdent.
De telles interprétations semblent autorisées par la tradition ; et l'on relève notamment dans le sepher yesirah cette formule qui semble évoquer matériellement le 515 :
« …. »
55
On peut remarquer maintenant que le nombre 55, outre que la somme de ses chiffres donne 10, présente une relation bien plus profonde avec le nombre 10, puisque 55 est à la fois le 10ème nombre triangulaire et le 10ème nombre de Fibonacci. 55 est donc le sommet d'un Lambda à dix étages dont les deux jambes correspondent respectivement à la série des nombres triangulaires et à celle des nombres de fibonacci.
On s'aperçoit que ce Lambda est le complémentaire, ou encore le symétrique de celui que l'on a vu tout à l'heure, qui coordonne les nombres de fibonacci aux nombres carrés, cette fois, de part et d'autre du sommet 144. Les deux lambdas peuvent être disposés l'un vis à vis de l'autre, les nombres « triangles » et « carrés » se déployant de part et d'autre d'un axe vertébral, formé par les nombres de Fibonacci.
En plus des rapports de symétrie « bilatérale » entre configurations gnomoniques (triangle / carré), on doit remarquer une symétrie entre le centre et les bords de la structure, symétrie qui concerne la forme même des fonctions mathématiques associées à ces suites.
Loi A. « Deux nombres triangles successifs donnent un nombre carré » Axiome dont la réciproque est « tout nombre carré supérieur à 1 est la somme de deux nombres triangles successifs ».
Loi B. « Deux nombres de Fibonacci successifs donnent un nombre de Fibonacci ».
Alors que les suites des nombres triangles et carrés peuvent être regardées comme « coengendrées », en ce que chacune peut être engendrée par une relation avec l'autre, la suite des nombres de Fibonacci est elle « auto-engendrée », particularité qui correspond à sa situation « axiale ».
D'autres structures mathématiques pourraient, complémentairement, être greffées sur la jambe gauche, puisque les nombres carrés sont les principes des équations de pythagore basées sur des triplets de nombres entiers, - équations qui, elles mêmes, sont susceptible d'opération d'exhaustion tridimensionnelle (gnomoniques), d'une part, mais en outre, de développement ou d'extension externes, dans lesquelles les 3 côtés du triangle sont ressaisis ensemble pour être rapportées à une réalité de dimension supérieure, qui les enveloppe. On voit donc que ce « lambda gnomonique » constitue un véritable paradigme, et comme un point d'ancrage pour le développement de ces appareils plus sophistiqués de la mathématique pthagoricienne que sont : la théorie du gnomon, et les équations de Pyhagore, à travers les deux triangles paradigmatiques de la nef.
On aperçoit déjà par ce chemin que le nombre 55 peut être considéré comme un « remplaçant » naturel du nompbre 144, en tant que principe bénéfique opposé à la Bête. Le nombre 144 se rattache au nombre 12, le nombre 55 au nombre 10 ; les nombres 10 et 12 exprimant chacun une forme différente de complétude, leur couple pouvant être vu comme le développement, ou l'avatar du nouage 5/6, pentagone / hexagone dont on a déjà envisagé diverses modalités.
Il nous reste à comprendre en quoi le nombre 515 constituait un meilleur candidat encore que le nombre 55.
Le 515 : saturation de la fonction miroir
Lima de Freitas a consacré au symbolisme de nombre 515 une importante étude, dans laquelle il reconstitue, à travers l'histoire de l'art et de la littérature, une partie de la tradition ésotérique associée ce nombre.
Il a d'emblée placé son étude sous l'angle adéquat, qui consiste à mettre au premier plan la nature palindromique de ce nombre, qui en fait une illustration parfaite de la fonction symbolique du miroir.
La fonction du miroir possède une relation évidente avec la connaissance, la science, qu'elle soit entendue au sens usuel ou au sens religieux et mystique. De Freitas illustre cela par ces citations en exergue de son livre, qu'il nous est agréable de citer in extenso, dans la mesure où elles ne sont pas seulement, pour celui qui en use, des illustrations, mais plutôt des attestations ou des preuves d'un chemin parcouru.
Cette connaissance intuitive qui est la plus haute des connaissances, celle des mystiques et des Fidèles d'Amour, ne peut se comprendre que lorsque l'on a postulé ce monde intermédiaire, ce lieu du miroir où s'expérimente la réalité imaginale. (G. Durand)
Dieu est ton miroir, c'est-à-dire le miroir dans lequel tu te contemples toi-même, et toi, tu es son miroir, c'est-à-dire le miroir dans lequel il contemple les Noms divins. (Ibn 'Arabi)
Le nombre 515 peut être regardé comme une saturation ou une mise en abime de la fonction du miroir.
On peut poser qu'un palindrome doit posséder 3 termes au moins (mais il n'a pas besoin d'en avoir d'avantage) pour exprimer la fonction du miroir dans toutes ses potentialités, à savoir, il doit comporter un être, son reflet, et un « milieu » qui est le pivot immobile, et qui, de par sa situation axiale et intermédiaire, peut être assimilé à la surface du miroir lui même.
Mais on comprend bien que lorsque ce milieu est l'unité, la force ce cette analogie est renforcée, puisque la fonction du miroir peut alors être assimilée à un objet ponctuel, minimal, et sans épaisseur, la forme même du chiffre 1 qui est celle d'un axe vertical, constituant un redoublement de cette analogie. La fonction d'axe et de pivot qui est celle du centre du palindrome, répond à la nature « ponctuelle » du nombre 1.
En second lieu, on peut remarquer que dans le nombre 515, non seulement la partie gauche se reflète dans la partie droite, et inversement, mais en outre, ces deux parties, ensemble, se reflètent dans l'unité qui est au centre (dont on doit se souvenir qu'elle correspond à une dizaine) ; ou inversement, c'est l'unité centrale et intérieure qui se reflète dans ces deux parties extérieures, qui peuvent apparaître comme l'expression, comme l' extériorisation des potentialités que cette unité recèle.
On voit que ce symbole prend immédiatement une dimension cosmique, dans laquelle l'unité centrale représente, l'axe du monde, le moteur immobile, le principe ponctuel infini de la manifestation universelle, et les deux 5, la dualité première, le macrocosme et le macrocosme, ou encore les spires de la manifestation universelle. Le nombre 5 avait souvent au moyen âge la même graphie que la lettre S, et l'on verra tout à l'heure que ce symbolisme graphique venant en soutien du symbolisme mathématique sera utilisé par des artistes comme Durer et Jorge Alfonso, tous deux représentants de la tradition ésotérique du 515, et affiliés à des organisations héritières de celle de Dante.
En tant que symbole cosmologique universel, le 515 peut être rapproché de deux autres symboles empruntés à la tradition pythagoricienne.
Analogie avec pentagramme. On peut paramétrer un pentagramme où les 5 points du pentagone extérieur (macrocosme) sont affectés de la valeur 100, les 5 points du pentagone intérieur (microcosme) de la valeur 1, tandis que le point central, qui est le centre des deux figures (de la même manière que la dizaine occupe une position « médiane » entre les centaines et les unités) est affectée de la valeur 10. De cette manière on obtient pour le pentagramme la valeur 515.
Analogie avec la nef. Dans la nef, on a, schématiquement, un « petit 5 », un « grand 5 », et en troisième lieu « la dizaine qui les sous tend », dizaine qui a, schématiquement, la forme d'un arc auquel les deux segments de valeur 5 sont rattachés par leurs extrémités. Où l'on peut voir à nouveau une analogie frappante avec le 515 ; toutefois, cette dernière analogie recèle une signification mathématique qui demande être développée de façon plus précise.
Le 515 et les équations de Pythagore
Une remarque mathématique de Lima de Freitas, relative au sujet même qui nous occupe, revêt une importance non moindre que celle qui concerne la fonction du miroir.
De Freitas semble avoir eu dès le départ l'intuition que le sens profond du 515 devait être recherché dans le théorème de pythagore et le triangle isiaque.
Il remarque :
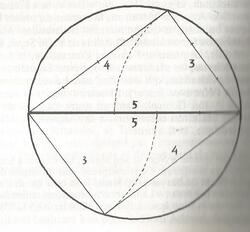
Si l'on inscrit (le triangle isiaque 3-4-5) dans un cercle, on s'aperçoit aussitôt qu'il est possible d'en inscrire un deuxième, mais qu'il n'y a de place que pour deux triangles. Cette duplication entraîne la superposition des hypoténuses, c'est-à-dire de côtés de valeur 5 des deux triangles. Nous avons donc, dans ce schéma, un diamètre de la circonférence où les deux hypoténuses coïncident ou se confondent, c'est-à-dire dont la valeur devient double, soit 2 x 5 = 10, l'équivalent de l'unité. Tout ceci a été expliqué par Jean Tourniac (…) mais ce que Tourniac n'a pas vu, c'est l'émergence, à partir du triangle doublé, du nombre du Messo di Dio 515. En effet si nous poursuivons la mise au carré des côtés 3 et 4 des triangles inscrits, nous obtenons le nombre 25 de chaque côté de l'hypoténuse commune ; l'extraction de la racine carrée de ces trois nombres : 25, 1 et 25 fournit 5, 1 et 5, autrement dit, le chiffre de l'envoyé de Dieu : 515.
Nous n'émettons de réserve que sur la manière dont de Freitas procède pour rapporter l'hypoténuse diamétrale de valeur cinq à l'unité, en supposant que les deux hypoténuse s'additionnent pour former le nombre 10, lui-même réductible à l'unité.
Même si le fait de considérer le 1 central du nombre 515 comme à la fois équivalent à la dizaine ou à l'unité est légitime dans l'exegèse symbolique de ce nombre, elle nous semble indue dans cette application particulière au théorème de pythagore.
En effet, nous pensons que, dans ce type d'exégèse, une opération arithmétique doit toujours être associée à l'opération géométrique qui lui est réellement analogue. Ainsi de la même manière que l'opération « construire un carré » sur un côté du triangle rectangle, équivaut rigoureusement à l'opération d'élever au carré le nombre correspondant à ce côté, de même, il nous semble que l'opération de mise en contact des deux hypoténuse de valeur 5 est l'analogue naturel, non pas de l'addition de ces longueurs, mais de leur mise en rapport rationnel, analogue à l'expression arithmétique 5/5. Cela ne change rien au résultat, qui demeure égal à 1 ; mais cette manière de l'interpréter ne nous semble pas seulement plus naturelle, mais elle revêt de bien plus importantes conséquences mathématiques.
En effet, s'il avait appliqué au triangle aurigène 1-2-racine5 le même traitement que celui qu'il applique au triangle isiaque, De Freitas se serait aperçu qu'on obtient, cette fois, non pas des nombres « dont les racines composent le nombre 515 », mais tout bonnement le nombre 515 lui-même.
Le théorème de pythagore se revèle alors être le medium, ou le module, grâce auquel la nef se transforme en un char doté de 2 roues, dont l'une, la roue aurigène de valeur 5-1-5, correspond à la RACINE de l'autre, la roue isiaque, de valeur 25-1-25. Et l'on peut remarquer parallèlement que, d'un point de vue angulaire, le triangle aurigène peut être également regardé comme la « racine » ou la « matrice » du triangle isiaque, puisque leurs angles respectifs par rapport à l'axe horizontal sont dans le rapport « double », ou « d'octave ».
Sous cet éclairage, l'appareil forme réellement un tout. En effet le triangle isiaque est déjà « premier » eu égard à son statut dans la série des triplets pythagoriciens, mais ici il est coordonné à un jumeau, un double, né avant lui, qui peut lui même être entièrement caractérisé par la qualification de « racine », ou de « matrice » du « premier ».
Il nous semble impossible d'aller plus loin dans l'exégèse mathématique du nombre 515.
L'arrière plan historique et spirituel de la prophétie
Suite aux découvertes de Benini, les travaux de René Guénon, Louis Barmont et Lima de Freitas ont mis en lumière l'arrière plan historique et spirituel qui permet de comprendre les attributs et la mission de l'Envoyé de Dieu. Deux événements sont à mettre en relief.
La destruction de l'ordre du temple dans les années 1310-1314. La fonction de guide spirituel dévolue à Saint Bernard dans la comédie montre assez la dévotion que Dante témoignait à ce personnage. Il ne fait pas de doute que, à travers toute l'Europe, pour de nombreux initiés d'obédience templière, la disparition de l'Ordre a dû résonner comme un événement apocalyptique. La catastrophe de l'ordre étant contemporaine de la rédaction de la comédie, elle a conduit Dante à porter des retouches à son texte, pour apporter une réponse prophétique aux événements les plus récents.
En arrière plan de ces événements dramatique, la prédication de Joachim de Fiore, encore très vivace dans les mémoires, sa théorie des trois âges de l'humanité et son annonce de l'instauration prochaine de l'Empire du Saint Esprit.
Ces circonstances historiques constituaient un climat propice à l'apparition de nouveaux messianismes.
La situation historique et psychologique de Dante était, au fond, très comparable à celle qui se dégage de l'apocalypse, d'après les lettres que Jean adresse aux fidèles des sept eglises. La visée de ces deux prophétie est avant tout consolatrice, et répond à une situation d'adversité et de détresse exceptionnelle.
Dante avait une conception toute personnelle de l'Empire, exposée notamment dans sa monarchie, dont les racines plongent dans la tradition italique, l'ancien pythagorisme romain et l'oeuvre de Virgile.
Le qualificatif de « lévrier » - à l'époque un chien de chasse – dévolu au 515, sa mission de Justicier et de redresseur de tort, (« sauveur d'Italie ») lui confèrent des attributs « martiaux » qui pourraient faire penser à ceux d'un « condottierre » ; tous ces caractères s'inscrivent, naturellement, dans cette conception de l'Empire.
Mais d'autre part, comme l'a remarqué de Freitas, le combat dont il s'agit est essentiellement spirituel. Le « redressement » historique symbolisé par la venue du 515 doit donc se situer principalement sur ce plan là, conférant à l'envoyé de Dieu une mission de conversion à l'Esprit Saint. Le 515 a donc aussi des caractères de prêtrise : ceux d'un « redresseur » et un « convertisseur », capable de « retourner les coeurs » vers Dieu.
Deux œuvres d'art exceptionnelles témoignent de la survivance de la tradition ésotérique du 515, deux siècles après l'époque de Dante.
La Melencolia de Dürer
De nombreuses études ont été consacrées au célèbre burin de Dürer. Parmi celles-ci, l'étude de Louis Barmont se distingue par certain caractère d'autorité, comme par son style étonnamment sacramentel, qui semble imiter celui de la gravure, et se nourrir de connaissances initiatiques directes, comparables à celles dont disposait Dürer.
En préambule, Barmont commence par fixer deux points qui étaient sujets à controverse.
L'astre qu'on voit voit dans le ciel n'est ni un « soleil noir », ni une planète, mais une comète observée dans le ciel de l'Europe entre 1513 et 1514.
Les objets représentés en haut à droite, balance, sablier, évoquent l'accomplissement des temps et la fin d'un cycle. Pour Barmont, la melancolia, « humeur noire », qui est le quatrième tempérament de la médecine grecque, renvoie implicitement à « l'âge sombre », autrement dit à l'âge de Fer ou au Kali-Yuga qui, dans les doctrines traditionnelles, est le quatrième âge de l'humanité. Mais la date de 1514 figurant dans le carré magique associe cette vision de la fin des temps à la commémoration d'événements tragiques qui en apparaissent comme les précurseurs : en effet, c'est en 1314 qu'eut lieu « le dernier acte de la tragédie templière ».
L'animal couché au pied du grand ange n'est pas un mouton, mais un lévrier ; et « nous ajouterons sans plus tarder que ce lévrier n'est autre que le Veltro dantesque, le Cinq-Cent-dix-et-cinq attendant l'heure de la lutte suprême contre la Louve antéchristique, assimilée au Six-cent-soixante-et-six du Théologien. » Barmont effectue une série de rapprochements entre la fonction du Veltro, telle que décrite par Dante, et diverses figures messianiques, empruntées à différentes traditions ; et il remarque que la fonction de cet envoyé de Dieu est double : d'une part, la conversion, la soumission volontaire des cœurs à la volonté divine, et d'autre part, la conduite de la lutte finale des orthodoxes contre les hétérodoxes... selon un scenario semblable à celui de l'Apocalypse. La fonction du 515 est donc à la fois martiale et sacerdotale.
Penchons-nous à présent sur la gravure. On peut remarquer qu'elle se laisse décomposer en trois parties, assez nettement distinctes. A droite, deux anges, entourés de toutes parts par une multitude d'objets aux connotations symboliques puissantes. A gauche, trois éléments de dimensions plus importantes que les objets de la partie droite, le solide, le lévrier et la sphère, qui semblent liés entre eux par une relation spécifique. Enfin, en haut à gauche, un événement astral effrayant, qui semble se dérouler dans l'espace-temps « ordinaire. » Cette disposition rappelle la doctrine des « trois mondes » ; et à ce sujet nous mentionnerons ces remarques, que nous devons à notre ami Walter Grimm
Je me demande si la séquence (astre lumineux - arc-en-ciel - chauve-souris) ne doit pas être rapportée à un plan différent de la première (solide – chien – sphère), symétrique, mais plus extérieur.
Dans ce cas là, on aurait :
Dans le monde informel : Les causes réelles et immuables de l’événement, occupant toute la partie droite de la gravure (anges, balance, sablier, carré magique, clochette).
Dans le monde subtil ou intermédiaire : L'opération adéquate autorisant l'actualisation de l'événement. C'est-à-dire, principalement la séquence [solide - chien – sphère].
Dans le monde extérieur : L'effet de l'opération : la séquence [ astre lumineux - arc-en-ciel - chauve-souris
L'astre est bien évidemment lumineux et c'est lui qui agit de manière apparemment désagréable sur la chauve-souris mélancolique, contrairement à ce que suggère l'article wikipedia dont nous avons déjà parlé, avec l'appellation singulièrement inapproprié de satellite sombre.
Entre ces trois plans, une échelle à 7 barreaux...
Si l'on raisonne en terme de degrés d'intériorité, ou d'imbrication : 1 < 2 < 3 (ce que l'environnement des symboles semble prouver suffisamment)Suivant cette interprétation, on remarque que les « causes subtiles » jouent un rôle de médiation entre les causes informelles et les causes grossières, exprimant les conditions de leur actualisation ; tandis que, à l'intérieur même de ces causes subtiles, le lévrier joue lui même un rôle semblable de médiation entre deux états ; par là il devient le véritable centre de l'ensemble des « opérations » décrites par la gravure, conformément à la fonction du 515.
Dans un série de commentaires rédigés au début des années 2010, Aliboron remarquait au sujet du chien :
Une simple assonance, en langue arabe, entre Kalb (chien) et Qalb (coeur)... m'a mis la puce à l'oreille.
(...) dans le même champ sémantique et sémitique, en arabe coranique la racine trilitère QLB, qui donne le mot qalb-coeur, signifie retourner. Et Dieu est dit être « Celui qui retourne les coeurs ».
Et il mentionne à ce sujet une doctrine cabalistique :
« Le Leb, le Coeur : L'Univers tout entier se compose donc de trois régions: le Téli en haut, de forme cubique; le galgal en bas, de forme sphérique; et, constituant un plan de démarcation entre les deux, le Leb, zone intermédiaire qui tient à la fois du carré et du cercle.
Cette interprétation permet, manifestement, d'assimiler la fonction du lévrier à celle du triangle cordial, comme élément nécessaire du retournement préalable à la circulature du quadrant.
Chacun sait qu'un chien, avant d'adopter cette position caractéristique de repos au pied de son maître, accomplit bien souvent plusieurs tours sur lui-même ; le comportement naturel du chien venant ainsi à l'appui de sa fonction symbolique.
Ces diverses annotations vont dans le sens de l'idée de Barmont, et permettent d'apporter plus de précisions à la fonction du Lévrier. L'action de « conversion » du Lévrier peut donc être précisée.
Elle implique une action de « redressement » analogue au Tiqqun cabalistique. Les remarques mathématiques de Freitas sur le 515 l'amènent précisément à le définir comme un agent « redresseur ». L'envoyé de Dieu intervient dans une situation où toute chose a été « déviée » de sa vérité et de sa nature.
Cette action de redressement a pour conséquence « le rétablissement de la plénitude ». Dans l'ordre des opérations géométriques, qui correspondent, ici, au degré de la manifestation subtile, le Veltro est l'agent de la médiation entre l'état de « troncature » du solide, et la « plénitude » de la sphère.
La fin d'un cycle, l'accomplissement des temps, marque toujours le départ d'un nouveau cycle. L'époque de la consommation des temps est donc aussi celle aussi ont réunies, reccueillies ou rétablies « dans leur intégrité », et donc leur complétude, en un certain point du monde, les conditions, les « germes » d'un nouveau départ et d'un nouveau cycle.
Dans cet ordre idées, on peut noter que si l'assimilation par Barmont de l'astre maléfique à une comète a pour elle de bons arguments, celle, également traditionnelle, qui l'assimile à Saturne apparait également très cohérente au point de vue du symbolisme. En effet, le symbolisme de cette planète, comme celui des racines SAT-STA auquel il s'apparente, est associée à la fois à l'idée de fin de cycle (le jour de Saturne saturday marquant la fin d'un cycle sénaire), à sa « SATuration », mais également à l'établissement ou l'inSTAllation d'un cycle nouveau. Samedi précédant, en effet, le jour de repos, ou de « stase » qui conditionne le départ d'un cycle nouveau.
La banderole
Barmont développe une série de remarques extrêmement pénétrantes au sujet du « phylactère » qui porte le titre de la gravure. L'écriteau est brandi par une chauve-souris, symbole des puissances obscures, en même temps qu'il peut correspondre à la découpe de ses ailes.
Selon Barmont, Dürer a volontairement dessiné son titre de façon qu'il puisse être lu comme une formule de 11 ou 12 lettres.
Dans le premier cas, on doit lire : Melencolia – signe « paragraphe » - I. Le signe I pouvant à son tout être interprété de deux manières, soit comme la forme romaine du chiffre 1, soit comme la lettre I, pouvant signifier ici l'Illusion, ou encore l'Ignorance propre à l'âge sombre.
(Précisons toutefois que c'est nous, ici et par la suite, qui assimilons le symbole « intermédiaire » au caractère d'imprimerie « paragraphe », Barmont n'y voyant qu'un symbole graphique indéterminé, qui ne serait ni une lettre, ni un chiffre).
Dans le second cas, la formule doit être lue : Melencolia S. I, les deux dernières lettres se référant alors au latin : Sanct Imperium.
On sait que Durer était originaire de Frankfort, où étaient conservées les reliques du Saint-Empire. La formule Melencolia Sanct Imperium pourra donc s'interpréter à nouveau selon deux ententes, ou bien comme exprimant la nostalgie du Saint Empire romain germanique, ou bien comme exprimant l'attente eschatologique de l'établissement de l'empire du Saint-Esprit, ces deux possibilités n'étant d'ailleurs pas contradictoires.
Barmont remarque en outre que, « par leur forme même, les deux lettres S. I. suggèrent le passage de l'errance indéfinie dans les spires successives de la manifestation (S) à la simultanéité et à la fixité axiale de l' « invariable Milieu » (I).
Quelles que soient les riches possibilités offertes par cette lecture, nous ne cachons pas notre préférence (ne serait-ce que d'un point de vue visuel) pour la première interprétation, selon laquelle la formule compte 10 + 1 lettres, séparées – ou reliées - par le symbole « paragraphe ».
De prime abord, les 11 lettres de la formule peuvent évoquer le 515, dont les éléments additionnés donnent aussi le nombre 11. En outre, l'étymologie du mot Melan/colia (noire-humeur) introduit dans ce mot une division naturelle en 5+5.
Quant au symbole d'imprimerie « paragraphe », qui ne devait pas être très ancien à l'époque de Dürer, il est dérivé du latin « signum sectionnis » - « signe de séparation ». Il se compose de deux S entrelacés. Or à l'époque de Dürer, le nombre 5 et la lettres S avaient souvent la même graphie. Ce symbole peut donc être compris comme contenant deux fois le nombre 5. Remarquons donc, en faveur des précédentes remarques de Barmont, que la formule S. I. contient, au point de vue graphique, tous les éléments nécessaires à la réalisation du nombre 515.
Barmont remarque en outre que Dürer a inscrit un point dans la zone intermédiaire et centrale du symbole « paragraphe ». Ce point peut donc figurer le 1 qui, dans le nombre 515, tient le milieu entre les deux chiffres 5.
Le symbole paragraphe, avec son point central, ne serait donc qu'un équivalent synthétique, ou une expression figurale des mêmes idées qui sont déployées dans la formule « contenante » Melen /colia-I
Les deux pouvant se résumer dans la formule :
5+5+1
Barmont remarque que, dans sa gravure Adam et Eve datée de 1504, « le cartouche suspendu à l'arbre de Vie porte la signature « Albert Dürer », suivi d'un signe qu'on serait tenté d'assimiler à un point d'interrogation ; à y regarder de plus près, on constate qu'il s'agit d'une spirale. »

Barmont considère ce signe comme se référant au lituus, insigne des augures qu'on retrouve dans la crosse des évéques ; ce signe attesterait ici de l'initiation de Dürer.
A propos de ce symbole, il note : « La forme du lituus, qui fut un des insignes du pouvoir des Pharaons avant de devenir celui des augures, symbolise, soit le « déroulement », le développement total d'un cycle ou d'un état, soit au contraire l' « enroulement », la résorption de ceux-ci dans leur centre principiel, selon le principe évolutif ou involutif du mouvement de rotation de la spirale. »
En suivant ce chemin, le signe « paragraphe » de la melencolia serait l'équivalent du double-lituus, et symboliserait ici la probable double initiation de Dürer, aux « petits » et aux « grands » mystères.
Très curieusement, Barmont omet de remarquer que, dans ce même cartouche de la gravure « Adam et Eve », on ne trouve pas seulement la spirale, mais, en bas à droite, un signe tout à fait identique à celui de la melencolia, et donc composé d'une « double spirale » à ceci près qu'il s'y présente en sens inverse.
Il nous semble que ce changement d'orientation est une indication extrêmement précise de la fonction du 515. La gravure Adam et Eve représente l'état du monde à l'époque de la consommation du « péché originel », autrement dit à l'origine de son état d'altération, ou de déviation. Dans la melencolia, le signe se retrouve « inversé », c'est-à-dire « redressé », sous l'action bénéfique du 515.
Barmont remarque enfin que, dans le signe « paragraphe » de la melencolia, les deux spirales se réunissent de manière à former, à leur jonction, un « losange curviligne marqué d'un point central ».
Et l'on peut remarquer que le losange, si on le considère comme la réunion de deux lambdas inverses l'un de l'autre, peut lui-même être considéré comme un symbole équivalent de celui de la double spirale, puisqu'il représente les deux fonctions essentielles de l'hénade que sont procession et conversion.
Le minuscule symbole situé au centre du symbole « paragraphe », le losange avec un point au centre, peut donc être vu comme une ultime expression synthétique de l'ensemble de la gravure, qui se déploierait à travers celle-ci comme par des cercles concentriques.
Losange avec un point au centre < symbole paragraphe / double lituus / 515 < formule « Melancolia – I » < ensemble de la gravure.
Etonnamment, cet ultime symbole présente une relation mathématique profonde avec le solide de Durer, dans sa formulation gnomonique. En effet, des six éléments qui occupent le centre géométrique de ce solide, quatre se répartissent sur un plan horizontal en forme de losange de 60/120 degrés, tandis que les deux autres s'ajustent le long d'un segment vertical, qui traverse ce losange en plein centre. L'axe vertical correspond à l'axe d'étirement du solide, (qui est son axe de symétrie majeur), et le plan horizontal, à son plan de symétrie bilatérale principal. Voir à ce sujet notre étude gnomonique sur le solide de Durer.
Si l'on reprend les idées associées par Barmont à la double orientation de la spirale, on saisit que le symbole paragraphe pourrait lui-même symboliser l'équilibre des forces universelles. Et à l'appui de cela (pour ceux qui douteraient encore que les principes du symbolisme obéissent à certaines règles) on peut remarquer que, dans plusieurs pays d'Europe de l'Est et du Nord, le symbole « paragraphe » est couramment utilisé comme un symbole de la Justice (ou parfois de la Police), autrement dit comme un équivalent de la balance.
Le rapprochement des deux gravures de Dürer permet de saisir le lien profond qui relie la Melencolia à l'oeuvre de Jorge Alfonso.
L'apparition du Christ à la vièrge, de Jorge Alfonso

De Freitas a raconté le destin extraordinaire de ce tableau, d'abord maquillé, puis débité en morceaux afin d'en faire disparaître la partie centrale, avant d'être reconstitué.
L'écusson au centre du tableau portait originellement le nombre 515. Le 1 initial a été ajouté après coup, pour faire croire à une date. De Freitas prend à notre goût trop de précaution à écarter la thèse qu'il soit authentique, tout en apportant de nombreux arguments qui en montrent l'incongruïté. D'abord le tracé du chiffre 1 est d'une main plus maladroite que les trois autres. L'axe de l'écusson passe tout près du 1 central du nombre 515, et l'ajout du 1 initial introduit un déséquilibre dans la composition qui est invraisemblable de la part d'un maître d'une telle excellence.
Ce tableau est donc le seul « document » historique où apparaisse directement le nombre 515, en dehors de l'oeuvre de Dante. De Freitas apporte les précisions historiques qui permettent de comprendre cette filiation. Alors que les organisations templières étaient pourchassées dans presque toute l'Europe, le Portugal est l'un des seuls pays qui ait été relativement épargné par ces persécutions. Certaines s'y sont donc maintenues plus longtemps qu'ailleurs, dans une relative tranquillité. Cependant, avec le progrès de l'inquisition au cours du XVIe siècle, la doctrine ésotérique associée à ce tableau était devenue indésirable. Le tableau fut d'abord maquillé pat l'ajout d'un chiffre 1 qui en masquait la signification. Mais cette mesure n'ayant pas suffi à « éteindre le scandale », il fut ensuite débité en planches, afin d'en faire disparaître la partie centrale. Les morceaux manquants furent miraculeusement retrouvés au début du XXe siècle, et le tableau rétabli dans son intégrité.
Remarquons d'abord que la conception du tableau semble entièrement dominée par le thème du miroir. L'action de la partie gauche : le rachat d'Adam et Eve, est en effet la conséquence directe, et comme le reflet de l'action qui a lieu droite, l'apparition du Christ, attestant de sa résurrection. Entre ces deux parties, l'écusson porteur du 515 joue bien le rôle d'interface, ou de médiation, conforme au symbolisme de ce nombre.
Mais on peut déjà relever que thème de l'Apparition, en lui-même, est déjà apparenté avec celui du miroir. Le miroir est un cadre d'apparition.Toute réalité qui apparaît, apparaît à quelqu'un ; et donc, toute apparition est comparution. Miroir et apparition peuvent, l'un comme l'autre, signifier la connaissance, en tant qu'ils définissent les conditions de celle-ci. Il faut qu'une réalité apparaisse, pour être connue.
Divers rapprochements peuvent être établis avec la Melencolia de Dürer.
Dans la partie gauche, la seule action qui ait lieu, c'est Adam qui présente la pomme restaurée dans son intégrité. Ce fruit miraculeusement reconstitué tient donc un rôle analogue à la sphère de la gravure de Dürer ; l'un comme l'autre expriment à la fois « l'action principale » de l'oeuvre qui les contient, et la fonction essentielle du 515 qui est le rétablissement de la plénitude.
Le lituus présent dans la banderole de la Melencolia, dont Barmont a rappelé la signification initiatique, est présent dans les chapiteaux des colonnes du Temple où se tiennent le christ et la vièrge.
Enfin on peut remarquer l'étonnante similitude entre la chauve-souris porteuse de l'inscription « melencolia I » et l'angelot porteur du 515. Ces deux êtres ailés, l'un maléfique, l'autre bénéfique, ont tous deux pour fonction d'éclairer la signification de l'oeuvre, et semblent témoigner d'un même événement, le premier « en amont », du point de vue de l'achèvement d'un cycle, le second en aval, du point de vue d'une réalité restaurée, marquant le commencement d'un nouveau cycle.

Une remarque mathématique de Lima de Freitas mérite d'être soulignée. Si l'on prolonge le trait noir - anormalement accusé - de l'escalier de gauche, jusqu'à ce qu'il rencontre le labarum tenu par le Christ, on obtient un angle de 54 degrés. L'angle complémentaire est de 126 degrés ; et les deux sont dans le rapport 3/7, qui est un rapport tétractique. Dans une tétractys de valeur 180, où chaque point vaut 18, l'angle de 54 degrés correspond au triangle, et l'angle de 126 degrés au septénaire central.

Cette tétractys rappelle la tétractys 360 dont on a parlé précédement. Ses points valent 18 eu lieu de 36, ce qui est parfaitement congrü en l'occurence, puisqu'elle correspond à l'angle plat, et donc au demi cercle de 180 degrés, tandis que la première correspond au cercle complet.
-
Par zalmoxis le 21 Août 2018 à 08:43
La peinture templière du solstice
à Montsaunès
par G. Denom et R. Bayou
Considérez comment croissent les lis: ils ne travaillent ni ne filent; cependant je vous dis que Salomon même, dans toute sa gloire, n'a pas été vêtu comme l'un d'eux. Mathieu, VI, 28.
0. LA SCENE PRINCIPALE : LA PORTE DES DIEUX
Le Sagittaire fléchant le Capricorne
Le carré du centaure
Une composition en 4 parties qui se lit en sens "horaire", à partir du coin en haut à droite : 1. Lancer de flèche. 2. Le rectangle de Fibonacci. 3. La Jérusalem céleste. 4. Le chrisme.
La scène principale représente le Sagittaire fléchant le Capricorne, symbole zodiacal qui désigne la période du solstice d'hiver, et du passage à la nouvelle année.
Le symbolisme des portes solsticiales est l'un de ceux dont René Guénon a le mieux démontré le caractère universel. Pour reprendre son vocabulaire, ce thème se situe à la jonction de deux catégories de symbolisme, l'un temporel, celui de la manifestation cyclique, et l'autre spatial, celui de la forme cosmique ; les deux catégories se trouvant ici coordonnées l'une à l'autre, et reconduites à un principe qui les précède, ou les sous-tend, puisqu'à une certaine division de temps, un tour d'horloge, qui est celui de l'année, est associée une révolution du ciel, qui suppose un parcours complet de celui-ci en tant que forme.
Dans de nombreuses traditions, les solstices d'été et d'hiver sont considérés comme des pôles de l'année, auxquels correspondent, à chaque extrémité de la voie lactée, les divisions du zodiaque dans lesquelles pénètre le soleil à ces époques de l'année, chacun de ces pôles constituant une porte du ciel par laquelle les âmes, respectivement, « descendent » dans la génération et la manifestation individuelle, ou « remontent », pour celles qui y sont appelées, hors du monde manifesté. Au solstice d'été, lorsque le soleil entre dans le signe du Cancer, est la porte des hommes, qui est celle de l'entrée dans la caverne cosmique, par laquelle les âmes descendent dans la manifestation ; tandis qu'au solstice d'hiver, lorsque le soleil entre dans le signe du Capricorne, est la porte des dieux, qui est celle de la « sortie » ou de la remontée des âmes vers l'éther supra-cosmique.
Au symbolisme de la porte s'associe très naturellement, dans certains cas, celui de la clef et de l'ouverture ; et dans cet ordre d'idées, René Guénon a relevé les nombreuses concordances qui existent entre le symbolisme de Janus, dieu de l'année, détenteur des « clés du temps », et la doctrine védique du vêda-loka et du pitri-loka, relative aux portes solsticiales.
Mais il constate aussi que ce symbolisme rencontre, en de nombreux endroits, un ensemble de traditions d'origine pythagoricienne, dont le témoin le plus éloquent est L'Antre des Nymphes de Porphyre.
Dans cet écrit extraordinaire, témoin d'un âge bien plus ancien de la tradition pythagoricienne, pour lequel les œuvres d'Homère et d'Hésiode jouaient le rôle d'ancien testament, Porphyre analyse le mythe homérique de la « caverne d'Ithaque », ou Antre des Nymphes, sanctuaire ou caverne initiatique dans laquelle des naïades se livrent à d'énigmatiques travaux.
« Les anciens, nous dit Porphyre, consacraient avec raison les antres et les cavernes au monde pris dans sa totalité ou dans ses parties. » Mais il remarque aussi que, chez les Perses comme ailleurs, les cavernes étaient souvent des lieux d'initiation ; le même sanctuaire pouvant avoir en même temps la fonction de symbole du monde sensible, et de lieu consacré aux rites initiatiques. A ces données persanes, explicites dans le culte de Mithra, Porphyre associe un ensemble important de traditions pythagoriciennes, dans lesquelles le zodiaque occupe une place centrale, pour lesquelles ses principaux témoins sont les écrits de Numénius et de Cronius.
« Ces deux auteurs disent qu'il y a dans le ciel deux points extrêmes... Le point estival est sur le signe du Cancer, le point hivernal sur le signe du Capricorne... On dit que le Cancer est la porte par laquelle descendent les âmes et le Capricorne celle par laquelle elles remontent... Mais c'est à juste titre que dans le récit d'Homère la région dans laquelle se situe la première porte est attribuée à la descente des hommes, tandis que celle où se situe la deuxième est attribuée non aux dieux, mais à ceux qui montent vers les dieux. Pour cette raison le poète ne dit pas : le chemin des dieux, mais des immortels, expression qui convient aussi aux âmes qui par elles-mêmes ou par essence sont immortelles. »
La flèche du centaure
Dans la riche tradition dont on a pris ici un aperçu, le solstice d'hiver constitue le pôle de l'année, en tant que point de suture, ou de nouage de l'ancienne ancienne année avec la nouvelle, d'une part, mais aussi, dans l'ordre spatial, en tant que période de retour du soleil dans un intervalle précis, entre deux divisions du zodiaque, après une révolution qui l'a vu accomplir un tour complet de la circonférence du ciel.
Mais l'essentiel se situe encore dans une troisième chose, qui est la conjonction ou la coïncidence de ces deux événements, et qui n'est, de soi, ni temporel, ni spatial, ni un « instant » particulier de l'année, ni un « point » particulier de la bande du zodiaque, mais précisément la coïncidence de ces deux réalités, qui peut apparaître comme la signature de leur commune origine, du principe indivis dont procèdent ces deux dimensions de la réalité que sont pour nous l'espace et le temps.
Et il faut convenir que la condition empirique de l'homme ne permet jamais de les séparer complètement l'une de l'autre. Au déploiement ou à la création d'un certain univers-espace, de dimension définie, correspondra, nécessairement, la « dépense » d'un certain quantum de temps, qui pourra, en dernière analyse, servir de référence pour l'un comme pour l'autre. Tout espace s'avérant ainsi lié, dès avant sa création, au stade de sa virtualité même, au temps minimum nécessaire à son déploiement.
Le symbolisme de la manifestation cyclique associe ces deux dimensions, temporelle et spatiale, sous l'angle de la complétude. Le soleil ne parcourt l'espace, ou le tour complet de la bande du ciel, que lorsque le temps de l'année est lui même écoulé.
C'est bien une telle opération de jonction, de réunion, qui est symbolisée par la sagittation du Capricorne par le Sagittaire. Le « sujet » de la peinture de Montsaunès est donc un nouage, un agrafage, dont la forme et la fonction sont parentes de celles du nœud labdaïque.
Le Sagittaire a trois flèches dans son carquois et la quatrième bandée, à son arc. En considérant la flèche bandée comme la flèche du solstice d'hiver, inaugurant le premier trimestre de l'année, les trois autres peuvent correspondre aux trois trimestres suivants de l'année à venir, et donc aux trois autres fêtes que sont les équinoxes et le solstice d'été. En outre, ces quatre flèches entrent nettement en résonance avec la structure de la peinture elle-même, qui est celle d'un carré divisé en quatre parties, dont le Sagittaire flécheur occupe la première, en haut à droite.
De l'autre côté du mur, une cinquième flèche est fichée dans le cou du Capricorne. Cette flèche peut être vue comme la même que celle qui est bandée par le centaure, ayant atteint sa cible quelques instants plus tard ; mais aussi, dans un autre sens, comme une « quinte » essence résultant de l'accomplissement du quaternaire qui l'a précédé, de son plein achèvement.
Une ancienne photo en noir en blanc révèle que la chèvre qui symbolise ici le Capricorne, aujourd'hui très détériorée, arborait sur son dos un « 4 de chiffre », ce qui appelle plusieurs commentaires. D'une part, ce symbole peut être vu comme un équivalent du chrisme qui occupe la dernière case de l'ensemble carré auquel appartient le centaure ; il peut donc comme ce symbole lui-même exprimer la plénitude, l'accomplissement de l'année, associée à la sagittation du Capricorne.

Mais d'autre part, cette chèvre n'est pas n'importe quelle chèvre, et l'on doit remarquer que la stylisation de ses cornes, dotées de 5 cors chacune, obéit à une convention particulière de la peinture médiévale, relative à la représentation de certains animaux « surnaturels » ou symboliques, tels que le cerf.

Une flèche traverse le cou de la chèvre-capricorne
Dans une légende commune à plusieurs vies de Saints (Hubert, Eustache), un jeune seigneur est tellement épris de chasse, qu'il ne peut s'abstenir de chasser le jour du Vendredi Saint. « Et comme il commençait à chasser, un cerf dix-cors, entièrement blanc, d'une taille extraordinaire, bondit et s'élança devant lui, l'entraînant dans les profondeurs de la forêt. Après plusieurs heures, le cerf ne montrait toujours aucune fatigue alors qu'Hubert était rompu. Soudain, le cerf s'arrêta net ! Dans une vision de lumière, Hubert vit le cerf blanc avec entre ses bois l'image d'une croix étincelante et il entendit une voix qui lui disait: "Hubert ! Hubert! Jusqu'à quand poursuivras-tu les bêtes dans les forêts ? Jusqu'à quand cette vaine passion te fera-t-elle oublier le salut de ton âme ?" ».
On voit que ce cerf crucifère à 10 cors est avant tout un symbole du Christ sacrifié, et de la passion, à l'image de l'agneau mystique de l'Apocalypse.
Le même cervidé apparaît dans la légende de Saint Eustache, à laquelle Dürer a consacré l'estampe ci-dessous.

Le Capricorne et le 515
Compte tenu de la nature nettement messianique de ce cervidé, Lima de Freitas n'hésite pas à le rapprocher de la tradition dantesque du 515, dans un symbolisme où les deux 5 correspondraient aux bois du cerf et le 1 au crucifix qui s'élève au milieu de son front : assimilation renforcée par le fait que la croix est considérée partout comme un symbole « axial ».
On comprend dès lors qu'une assimilation très naturelle ait pu s'effectuer, d'un point de vue ésotérique, entre le « temps messianique » symbolisé par le cerf 10 cors et le 515, qui est un temps d'accomplissement, de « remplissement » de la prophétie, et le temps cosmologique de « la porte des dieux », associé lui aussi à des conditions de « plénitude » et d'accomplissement d'une période donnée qui est l'année. Et de fait, chrisme, 4 de chiffre et crucifix peuvent être considérés comme trois variantes d'un seul et même symbole archétypal, qui est celui de la croix.
Sous ce regard, la chèvre-capricorne pourra donc être vue comme aspect particulier de la puissance du 515, s'exerçant non dans le temps historique de la messianité, mais dans le temps cyclique qui est celui du cosmos.
Sagittation du Capricorne : la "flèche du Parthe" dans la tradition astrologique
Le thème zodiacal du Sagittaire lançant sa flèche sur le Capricorne est illustré dans cette enluminure (extraite des Très riches heures du duc de Berry), où le Capricorne est représenté sortant d'un coquillage, à droite de la frise « vesicatoire ».

Dans son étude sur le symbolisme du cerf et du centaure (à lire ici) Jean Bayet remarque que "le centaure sagittaire visait soit le Scorpion, soit le Capricorne... mais de règle, lorsqu'il se retourne pour tirer (cas de la miniature du duc de Berry) c'est le Capricorne qu'il vise..." Et plus loin il constate que "le Capricorne est souvent représenté par un bouc ou une chèvre.... ".
Un symbolisme corroboré par la situation de la peinture
La scène peinte sur le mur se déploie sur un axe horizontal qui, relativement à l'axe de la nef (est-ouest) est orthogonal, donc un axe sud-nord.
On voit que l'intégration de la peinture dans l'espace de l'église ne doit rien au hasard. L'action de sagittation du Capricorne par le centaure se déploie bien sur l'axe Sud-Nord qui est celui des solstices ; et la situation de la peinture sur le mur d'Occident conduit à une assimilation naturelle entre le couchant du jour – l'Ouest – et le couchant de l'année qui est le solstice d'hiver.
Les deux fêtes de St Jean, associées aux solstices d'hiver et d'été, étaient associées au feu et à la lumière. Et c'est ce qu'on doit avoir à l'esprit en remarquant, à Montsaunès, la dimension extraordinaire de la fenêtre d'Occident, chargée de recueillir le maximum de la lumière du soleil à l'instant même où il se couche et meurt, - fenêtre sous laquelle la peinture du solstice fait l'effet, par la modestie de ses dimensions, d'un commentaire en bas de page, ou d'une légende.
Le chasseur chassé : la doctrine du sacrifice
Il resterait à expliquer comment le 515, plutôt "chasseur" chez Dante (... qui occira la larronnesse et le géant qui fornique avec elle) se mue en chassé (chèvre) dans la présente circonstance.
Paradoxe qu'il semble impossible d'expliquer, sans une compréhension des doctrines métaphysiques du sacrifice, en vertu desquelles toute création, (et donc, toute création d'univers, toute manifestation), est le fruit d'un rite sacrificiel primordial dans lequel le sacrifiant, le sacrifié, l'autel, et le couteau, ne sont qu'un seul même officiant. Sur ce sujet nous ne pouvons faire mieux que de renvoyer aux travaux de Coomaraswamy.
D'une manière assez analogue, nous avions remarqué la ressemblance, l'étrange air de famille qui existait entre le « nombre de la bête » (666) et celui des élus rassemblés autour de l'Agneau du sacrifice (6 + 6) x (6 + 6). Parenté qu'on doit interpréter comme la marque du fait qu'ils ne sont fondamentalement qu'un.
I. LANCER DE FLECHE – LE CENTAURE CHIRON, DISCIPLE D'APOLLON – ASPECTS DE LA RELIGION DE PYTHAGORE

En préambule aux remarques de ce chapitre, nous devons avoir à l'esprit le fait qu'au sein du premier cercle des disciples de Pythagore, Pythagore n'était pas seulement considéré comme « un prêtre du soleil », mais bien réellement comme un avatar d'Apollon Hyperboréen, actif et présent dans la vie de tout homme, chaque fois qu'il sort de son lit.
La religion d'Apollon et celle de Pythagore ne sont donc, véritablement, qu'une seule et même chose.
« Apportez moi mon arc et ma lyre »
Le cri poussé par Apollon à sa naissance, après avoir rejeté les vêtements-limitations dont on l'avait affublé, annonce qu'il possédait de toute éternité ces instruments à corde, capables de délivrer :
- pour l'un, la vérité (la lyre étant le support de sa prophétie, de sa parole oraculaire),
- et pour l'autre, la mort (le déchaînement de la vengeance d'Ulysse sur les prétendants, entièrement orchestré par Apollon, dont on célèbre ce jour-là la fête, est inauguré par un examen rituel de son arc, explicitement semblable au rituel d'accordage d'un instrument, pratiqué par tout musicien).
Or, nous savons que l'univers est né d'une tension. Et une tension ne présuppose que deux choses : d'une part, une corde, et d'autre part un support, un châssis, capable de supporter la tension de cette corde : l'arc ou la lyre.
« Apportez-moi mon arc et ma lyre » (Hymne homérique à Apollon)
Il est essentiel de comprendre que l'arc et la lyre d'Apollon existaient, sinon, avant la naissance d'Apollon, du moins « en même temps » que lui comme une excroissance gémellaire. Et les victoires d'Apollon attesteront, d'une certaine manière, qu'il est impossible de jouer correctement de ces instrument, si vous n'en étiez pas doté au moment même de votre naissance.
Dans les instruments d'Apollon se remarque, toutefois, une tension de type bien particulier, qui est la tension du retour, ou du retournement, et que l'on retrouve dans divers mots formés à partir de la racine grecque « palin », « retourner ». L'arc et la lyre appartiennent à une même famille d'instruments, qui peuvent être palintones - par le jeu de tensions opposées entre main d'arc et main de corde - ou palintropes, pour l'arc composite, dont la forme bandée inverse la forme au repos.
Et on se rappellera qu'il est courant, dans l'art médiéval, de voir le Sagittaire flécher le Capricorne en se retournant, même si ce n'est pas le cas sur notre peinture.
En physique pythagoricienne, la « tension du retour » porte le nom de tension de conversion. Etant de nature « centripète », elle ne peut survenir qu'au sein d'une réalité parvenue à un instant critique de son développement, qui est l'aboutissement d'une certaine procession. Mais d'autre part, comme le rappelle justement Maël Mathieu : « seul peut procéder ce qui est capable de se convertir ». Autrement dit, la fin est la condition du commencement.
Le thème du retournement, en tant qu'il découle de la science apollinienne de l'archer, établit un lien entre l'action du centaure et le thème du palindrome, retournement mathématique qui sera développé, dans toute sa richesse métaphysique, dans la troisième division du « carré du centaure », représentant la Jérusalem Céleste.
Le centaure Chiron, jonction entre le pythagorisme et la médecine
Les centaures sont, dans la mythologie grecque, des créatures plus remarquables par leur brutalité que par leur sagesse. A une exception près toutefois : le centaure Chiron, disciple ou fils adoptif d'Apollon.
Apollon a tué (par le feu) la mère de Chiron, avant de sauver l'enfant des flammes. Il en a ensuite fait l'éducateur de son fils Asclépios, dieu fondateur de la médecine. La tradition précise assez souvent que "le savoir d'Asclépios" est le savoir de Chiron.
Le centaure Chiron est donc le medium mythologique qui forme la jonction entre la science d'Apollon, et la tradition de la médecine grecque, (que d'aucuns, comme Jean-Luc Périllié, n'hésitent pas à qualifier de pythagoricienne), se revendiquant de son fondateur mythologique : Asclépios.
Rappelons qu'Hippocrate, rédacteur du serment prononcé aujourd'hui encore par tous les médecins, était lui-même un asclépiade et conservait la généalogie de son ascendance jusqu'à Asclépios et Apollon.
André Charpentier considère le serment d'Hippocrate comme un document chiffré pythagoricien régi par le nombre 666 (voir son étude ici). Le serment se fait par Apollon, Asclépios, Hygie et Panacée, qui constituent une famille divine pythagoricienne - le serment serait équivalent aussi au serment par "la sainte tétractys". On remarquera que le dernier membre de la lignée : Panacée, contient la racine « pan », « tout », qui correspond à l'état de « complétude » de la tétractys.
Chiron occupe donc une place de médiateur, ou d'intercesseur entre les deux premiers personnages de cette lignée divine pythagoricienne.
La piste du centaure peut même être poursuivie au delà du seul champ hellénique et de la religion apollinienne, puisqu'on en trouve la trace, dans un plus large champ indo-européen, dans différents mythes relatifs à la fois au cheval et aux origines de la médecine. Une étude bien documentée nous apprend en particulier que, selon Dumézil, le mot "Kentauros" pourrait être un équivalent du sanscrit "Gandharva". (Valérie Gitton-Ripoll : Chiron, le cheval-médecin ou pourquoi Hippocrate s'appelle Hippocrate)
Ces éléments mythologiques ne doivent en rien occulter la dimension zodiacale et calendaire qui reste fondamentale, dans le contexte pythagoricien.
Ce n'est sans doute pas sans motif que le centaure a donné naissance, non à une constellation, mais à deux, le Sagittaire et le Centaure, qui font de cette créature mythologique un acteur familier de la machine du ciel.
Quant à la fonction de flécheur qui est attribuée au centaure dans le symbolisme du solstice, elle s'accorde assez bien avec l'étymologie, qui fait dériver son nom (Kentauros) d'une fonction primitive de « piqueur » de bétail (kentôr).
Chi-ron le cent-aure, la tentation du jeu de mot
Une assonance entre Chiron et le chi-rô du chrisme, établit une connexion entre le début et le terme de la séquence du « carré du centaure », entre l'alpha et l'oméga. En ayant à l'esprit que cette connexion entre la fin (de l'année) et le début (de la suivante) est – bien qu'en sens inverse - le sujet même de la peinture du solstice.
En second lieu, on peut s'arrêter à la connotation arithmétique du nom du CENTaure. En effet, en fixant à 66 « l'ouverture de la mandorle » - pour des raisons autant symboliques (démiurgisme), qu'architecturales (mesures du panthéon de Rome) - André Charpentier associe le nombre 99 au « rayon céleste » qui embrasse cette figure, et le nombre 100 à ce rayon complété par son « pôle ».
Si l'on relève en passant que : 100 / 66 = 1,515151515... on voit que ce chemin ne nous éloigne pas du 515.
Ce nombre cent que les peintres templiers, sans l'avoir recherché, entendaient vraisemblablement dans le nom du centaure, semble donc résonner de façon très heureuse avec la fonction du rayon dardé par le Sagittaire, ainsi qu'avec sa position de porte, ou de pôle, pour l'axe du monde.
Nous allons voir que cette fonction du Sagittaire peut encore être illustrée sur un autre plan, qui est celui de la tradition alchimique.
Point de vue opératif
D'un point de vue alchimique opératif, Aliboron explicite le symbolisme du Sagittaire selon deux perspectives complémentaires :
- Comme une des « saisons » de l’Oeuvre, donc comme métaphore convenue sans rapport direct avec l’astrosophie, il se situe à la fin du Solve, volatilisation du Fixe. Phase dite de Jupiter (qui trône en Sagittaire et Poissons) succédant à la saturnienne. Entre Nigredo et Albedo (noire puis blanche) on lui attribue du... gris, virant au verdâtre car le Dauphin nouveau-né (Saturnie végétable) y vire au Vert léonin.- D’un autre coté, si l’on en croit l’astrobiologie selon Rabelais, il se trouve qu’entre Scorpion et Sagittaire, précisément, se présente une « fenêtre » cosmique propice à la « descente » du Spiritus Mundi...
La chasse spirituelle : René Alleau, à propos des lévriers et autres chiens pythagoriciens

Dans la première partie de cette étude sur la tradition du nombre 515, nous avons abordé la question des liens entre le veltro dantesque et le chien couché de la Melencolia de Dürer, en nous bornant, pour l'essentiel, à résumer les travaux de Louis Barmont et Lima de Freitas sur le sujet.
Dans ses Enigmes et symboles du Mont Saint-Michel, René Alleau offre des remarques sur le lévrier, se rapportant à une miniature de Jean Fouquet illustrant la fondation de l'ordre de Saint-Michel (XVs) - remarques que nous reproduisons en intégralité, en raison de leur intérêt pour notre étude.
En plus de l'éclairage hermétique qu'elles apportent au thème médiéval de la chasse spirituelle, ces remarques peuvent nous questionner à un autre titre, du fait que l'on sait, aujourd'hui, que la légende de Saint Michel a eu pour fonction de "recouvrir", en le christianisant (aussi bien du point de vue mythologique que géographique), un ancien culte païen de type nettement apollinien, dont le Mont Saint-Michel constituait sans doute l'un des hauts lieux, comme le Monte Gargano en Italie. Ce rapport de continuité, ou plutôt de relève théologique assumée permet de voir dans la victoire de l'Archange Saint Michel sur le dragon, inspirée de l'Apocalypse, une quasi réplique de celle d'Apollon sur Python.

Frontispice du manuscrit enluminé
« Statuts de l'ordre de Saint-Michel »
« Aussi doit-on déchiffrer les moindres détails allégoriques de la miniature illustrant la fondation de l’Ordre car on ne laissait à l’artiste aucune liberté dans le choix d’emblèmes qui revêtaient alors une grande importance héraldique et politique.
On trouve deux chiens analogues au château du Plessis-Bourré, dans la « demeure philosophale » du trésorier de l’Ordre de saint Michel. C’est à Eugène Canseliet que l’on doit d’avoir signalé, en effet, dans son ouvrage : Deux Logis alchimiques la signification hermétique des caissons peints de la salle de garde du château, dans le Maine-et-Loire. Deux interprétations du thème du « chien blanc » figurant sur les miniatures peuvent être proposées. Selon l’une, on aurait évoqué par ces « armes parlantes », le mot « Lévrier », attesté, au XIIe siècle, déjà dans Enéas, et qui signifie, proprement, « chien qui chasse le lièvre ». Au XIVe siècle, Nicolas Oresme le nomme « Levron » et, pour la femelle « Levronne ». Il est probable que l’on prononçait alors « Levrier » sans accent.
Si l’on admet cette hypothèse, l’allégorie héraldique du Levrier joue sur l’homophone L’Oeuvre y est. On peut aussi « blasonner » sur Oeuvrons aile en chef, devise des travaux mystiques des chevaliers de l’Ordre sous la haute protection de l’Archange. Rappelons, en effet, avec Grasset d’Orcet, que l’on pouvait aussi « blasonner » en « assonnant sur la lettre L », selon des règles trop compliquées pour être examinées ici.
Selon la seconde hypothèse, plus probable, à notre avis, il ne faudrait pas voir ici un lévrier mais plutôt un chien courant blanc que nos anciens auteurs nommaient "baud", chien-cerf, ou chien muet. Jean Nicot, dans son Thrésor de la langue françoyse, précise : "D'aucuns les nomment chiens muets, d'autant que, venant le cerf au change, ne disent mot jusqu'à ce qu'il soit hors". Et Nicot rajoute qu'à cause de leur silence, ces chiens étaient nommés pythagoriciens.
Selon cette hypothèse, ce chien blanc ferait allusion au silence imposé expressément par les statuts de l’Ordre aux chevaliers de Saint-Michel sur tout ce qui concernait leurs délibérations. Mais on peut aussi y voir une image de la “quête initiatique” et de la “chasse spirituelle” dans laquelle l’intuition joue un rôle aussi déterminant que le flair dans la chasse matérielle. La comparaison entre le cerf “aux bois rayonnants” et Jésus qui mène l’âme altérée aux “sources de l’éternelle sapience” se retrouve dans la plupart des allégories mystiques du XVe siècle.Afin de préciser qu’il s’agit en effet d’une quête des vérités supérieures ou “célestes”, Jean Fouquet a situé au même niveau que celui du tableau du combat de saint Michel, remarquable par le ciel étoilé qui sert de fond à la composition, une lucarne ouverte en haut du mur, laquelle, à première vue, ne présente aucun intérêt ornemental car ce détail étrange déséquilibre au contraire, la perspective rigoureusement ordonnée du tableau. En fait, il s’agit là d’un exemple de la cabale phonétique, chère aux disciples d’Hermès, et qu’il faut connaître si l’on désire entendre leur enseignement secret, tel que l’expriment, allégoriquement, de nombreuses oeuvres d’art médiéval. » Dont l’ “héraldique sacerdotale” est condensée dans la “Légende Dorée” de Voragine.... voir par ex, les étymologies “fantaisistes” qui la parsèment.
« On doit savoir, d’abord, comme le rappelle A. Dauzat, dans son dictionnaire étymologique, que le mot “lucarne” dérive de la lucanne (XIVe siècle) emprunté au provençal lucana, “lucarne”. Ce mot jouait ainsi homophoniquement sur “lucarne”, nom d’un coléoptère vulgairement appelé “cerf-volant”, insecte caractérisé par les dimensions considérables de ses mandibules, dentées et saillantes, analogues aux bois des Cervidés. L’allusion héraldique au thème du “cerf-volant” ou du “cerf-ailé” confirme ainsi celle qui se rapporte au “chien-cerf”, au premier plan de la miniature. (...) Rappelons que le “Cerf-volant” était l’emblème de Charles VI et de Charles VII, “peut-être en raison de la prophétie fameuse à laquelle fait allusion Christine de Pisan dans le poème où elle célèbre les exploits de Jeanne d’Arc :
« Car un roi de France doit être
Charles, fils de Charles nommé
Qui sur tous rois sera grand maître
Prophéties l’ont surnommé Le cerf volant... »Bref, “la lucarne” ouverte du coté du ciel et de saint Michel, tel qu’il est figuré sur le tableau central, évoquerait ainsi la protection accordée au “Cerf-volant” de France par le Roi du Ciel. Ce serait là un rappel des victoires miraculeuses de Jeanne d’Arc et de la légitimité divine du pouvoir royal, depuis le sacre de Reims.”
Le lucane et l'axe des nœuds lunaires
Reprenons les précisions entomologiques de René Alleau. Dans le monde des insectes, le lucane est effectivement un cervidé.
Dans ses Métamorphoses, le grammairien Antoninus Liberalis fournit à son propos des informations qui intéressent notre enquête : la tête du lucane « ressemble, avec ses cornes, à la lyre que l'on fait à la carapace de tortue ».
En examinant l'Hymne homérique à Hermès, nous pouvons voir que le thème du retournement est au cœur de l'invention de la lyre. La tortue est en effet un animal bien singulier, qui « pourvue d'une peau de pierre » selon Plutarque, et même si elle est capable d'émettre un petit sifflement, est présentée comme muette (anaudos) par les grecs. Nous dirions aujourd'hui « muette comme une tombe », et précisément, la tortue trouvera une voix (phônê) après sa mort lorsqu'elle sera transformée en lyre. Cette transformation sera l'œuvre du jeune dieu Hermès, qui, trouvant une tortue devant la grotte du mont Cyllène où il vient de naître, l'amène à l'intérieur après l'avoir retournée sur le dos.
Mais les grecs avaient aussi observé l'affinité de la tortue avec le monde souterrain, le monde chamanique « des envers ». En s'enterrant dans le sol pour hiberner, elle en fait autant que ses petits, puisqu'elle se sert de la terre pour retourner dans le monde des vivants. L'étymologie latine tartaruca (bête du Tartare) renvoie-t-elle à cette représentation grecque de la tortue ?
Un dernier aspect du retournement est offert par le concours musical opposant Apollon et Marsyas. Rappelons que le dieu ruse en imposant cette condition à son adversaire : « Je te défie de faire sur ton instrument ce que je fais: tourne-le à l'envers ». Nous avons déjà mentionné la qualité intrinsèquement palintonique de la lyre, mais Apollon en exploite ici une propriété extensive, celle de jouer en la retournant dans l'espace. Propriété que ne possède pas la flûte, et qui valut à Marsyas d'être écorché vif... John Scheid commente : « car si la lyre est l'instrument grâce auquel les âmes peuvent remonter à la lumière, une lyre inversée devient l'instrument grâce auquel elles sont renvoyées dans l'obscurité de la mort ».
Cette topologie des lyres, à l'endroit et à l'envers, nous a frappé par sa ressemblance avec les emblèmes des nœuds lunaires qu'a conservé la tradition astrologique indienne. Rappelons que ce sont des points virtuels associés astronomiquement aux éclipses, et décrits mythologiquement comme la tête et la queue du dragon.
Il nous semble possible de superposer (ici encore, en un sens convenu et non astrosophique) l'axe des nœuds, c'est-à-dire l'axe du dragon, à l'axe des solstices : la tête du dragon - ou lyre à l'envers - représente la descente des âmes associée à la porte du Cancer, alors que la queue du dragon - ou lyre à l'endroit - représente leur remontée dans le Capricorne. Correspondance qui s'accorde avec les données de la tradition indienne, qui fait de Rahu (tête du dragon, dépourvu de corps) une puissance de matérialisation et de Ketu (queue du dragon, dépourvu de tête) une puissance mystique de renoncement. (note 1)
II. LE RECTANGLE DE FIBONACCI.

Il s'agit d'un rectangle quadrillé de côtés 5 et 8, dont toutes les cases sont hachurées par une diagonale, à l'exception d'une zone de 9 cases située en bas à gauche, où les cases sont hachurées par deux diagonales, formant une croix, et où les divisions horizontales sont absentes. Cette différenciation est suffisante pour identifier immédiatement un rectangle de Fibonacci de rang 5, mais aussi, pour reconstituer toutes les autres parties du rectangle, dans leur développement en spirale.

Dans tout rectangle de Fibonacci, l'avant dernier carré joue le rôle de médiateur, (ou de « médian », au sens défini par les médiétés pythagoriciennes à trois termes), puisqu'il occupe une position intermédiaire entre "ce qui conclut", et "tout ce qui précède".
Dans le rectangle de Fibonacci de rang 5, et de côtés 5 et 8, le médiateur est bien le carré 3, intermédiaire entre ce qui conclut (le carré 5), et "tout ce qui précède" (l'addition des côtés des carrés 1 et 2 qui donne 3). Le hachurage de ce carré 3x3 au sein du rectangle revient donc à mettre en évidence, dans celui-ci, cet élément médiateur.
Il existe plusieurs méthodes, également légitimes, pour paramétrer le départ de la série des nombres de Fibonacci dans le rectangle du même nom, dont l'une, la dernière que nous mentionnerons, peut être regardée comme plus « pythagoricienne » que les autres.
- La première consiste à décomposer le carré long, ci-dessus distingué par un pavage « mosaïque » comme en regorge l'église de Montsaunès (pavages dédiés aux Muses, et non à Moïse...) en deux petit carrés « atomiques » de 1x1. Dans ce cas la suite de Fibonacci sera représentée par les « incréments » carrés successifs qui s'agglomèrent à cette matrice (1, 1, 2, 3, 5....)
- Une autre manière consiste à paramétrer les états successifs du rectangle global. Dans ce cas les nombres de Fibonacci se développeront par paires « conjointes », correspondant aux côtés du rectangle, donc chacune mesure un nouvel « état » de ce rectangle ; et la série pourra même alors débuter au stade « zéro », stade où le rectangle n'est encore qu'un segment de largeur 0 et de longueur 1. La série prendra alors la forme (0,1), (1,1), (1,2), (2,3), (3,5)...
- Enfin une troisième méthode consiste à écarter les deux premiers éléments de la série précédente, en considérant que ni le segment (0,1), ni le carré de 1x1, ne sont véritablement des rectangles, et que le premier « vrai » rectangle de Fibonacci est le « carré long » de 1x2.
Cette dernière solution est, sur le plan logique, la plus conforme à l'esprit de la mathématique pythagoricienne.
En effet, en mathématique pythagoricienne, la catégorie géométrique des « quadrilatères » n'est pas pertinente, du fait que le carré et le rectangle sont subordonnés à deux catégories logiques rigoureusement distinctes, dont le première est la catégorie du Même, et la seconde celle de l'Autre. Dans cette optique, le premier « vrai » rectangle de Fibonacci, qui joue pour la série des suivants le rôle de graine, ne peut être que le carré long de 1x2. C'est seulement dans cet objet qu'est « libérée » au sens logique la catégorie de l'Autre, par la duplication d'un objet (le carré atomique) qui relève lui-même de la catégorie « antérieure », et plus primitive du Même.
On voit que, dans cette logique profonde, la catégorie de l'Autre n'est complètement libérée qu'au terme d'un processus de développement qui, à partir du point, compte 4 étapes : point, segment, carré, double carré, et qui n'est pas sans analogie avec celui de la tétractys.
Mais une autre raison, plus profonde encore, rend cette façon de voir préférable, d'un point de vue pythagoricien. Le rectangle de Fibonacci est un rectangle se développant par incréments successifs de carrés, dont le rapport des côtés tend vers la valeur : φ.
Or cette valeur φ, vers laquelle le rectangle tend dans sa croissance indéfinie sans jamais pouvoir l'atteindre, se trouve enfermée, sous forme rigoureusement exacte, dans les mesures du carré long qui est sa matrice, ou sa graine.
On a vu qu'il était possible de l'extraire de deux manières différentes. Soit par le rapport des côtés du triangle rectangle qui forme le demi carré long.
(√5 + 1 ) / 2 = φ
Le carré long
Soit en considérant seulement l'hypoténuse de ce même triangle, qui est donc la diagonale du carré long, dont la valeur est égale à √5, en sachant que :
√5 = φ + 1/φ
Le rapport doré exact se trouve en effet enfermé dans la diagonale du carré long, sous la forme d'un couple gémellaire, formé de l'addition du nombre d'or et de son inverse. Cette diagonale-hypoténuse apparaît donc comme la « corde » primitive, porteuse du rapport doré, dont la « résonance » ordonne la croissance et le développement de « l'univers manifesté » que figure, ici, le rectangle de Fibonacci.
De ce point de vue, qui compte le carré long comme étape « un », le grand rectangle de valeur 40 se constitue en 4 pas.
La production du nombre 40 semble donc correspondre, dans l'esprit des auteurs de la peinture, à un état de développement du rectangle faisant apparaître une forme de « complétude », ou du moins de « développement suffisant ».
Et l'on peut remarquer au passage que, si on attribue la valeur "1" au carré long, en tant qu'originaire, ou élément supposé insécable (premier "vrai rectangle" de Fibonacci), alors la structure qui s'ordonne autour de lui peut évoquer (en vue certes un peu formelle, et « cursive ») le 515 :
(2+3) (1) (5)
Cette supposée complétude du rectangle de valeur 40 nous permet d'induire (au moins à titre d'hypothèse) que la relation que nos templiers percevaient entre le carré long, rectangle matriciel, et le rectangle 40, présentait une certaine analogie avec la relation graine – gnomon (plus précisément : graine / polygone gnomonique de rang immédiatement supérieur) à laquelle nos études nous ont familiarisés. Et de la même manière, on peut penser que le rectangle-source, le carré long, pouvait être perçu comme un élément détachable de la structure, comme un « patron » ou une pierre d'achoppement, ou encore comme un « vide » créateur... de la même manière qu'une graine peut être détachée de son gnomon.
Le rapport doré enfermé dans le carré long matriciel étant aussi le conduit, le principe « attracteur » ou directeur, de la croissance du rectangle, nous sentons que la métaphore de la graine, de la croissance végétale ou biologique, est ici particulièrement pertinente.
Nous sommes bel et bien ici au cœur de la doctrine pythagoricienne de la Nature, au sein de laquelle le rapport doré joue le rôle de « fil d'Ariane », permettant « la sortie du labyrinthe », permettant que ce qui, dans une supposée « graine d'univers », serait enfermé à titre de pure virtualité ou de germe, puisse, de proche en proche, par une suite de rapports immédiats et processionnels à « soi-même », advenir dans le monde de la « manifestation », sous la forme spatio-temporelle que nous connaissons, qui est celle d'un processus, d'un développement naturel.
La pulsation alternante du 5
Remarquons que le carré long, figure la plus simple contenant la dynamique du 5, est coextensif à la mandorle :

Dans son étude sur L'œuf du monde, André Charpentier attribue à la puissance du 5 la propriété de mise en abîme alternée, qui permet de construire une mandorle yin (horizontale) au sein d'une mandorle yang (verticale). Processus qui peut se poursuivre indéfiniment, et qui dévoile, selon sa belle expression, l'œil qui voit tout :
Mais, continue l'auteur, la figure la plus évidente de cette loi universelle est le Pentagramme pythagoricien, qui fait alterner, et donc vibrer ou flamboyer, les deux formes du pentagone, convexe et étoilé : « propriété unique dans toute la géométrie, qui fait de l'Etoile flamboyante le meilleur symbole de la vie universelle ».
LUX et carrés magiques
Avant même de nous demander quelles idées les templiers pouvaient associer au rectangle de Fibonacci, nous devons avoir à l'esprit qu'une figure se définissant comme un « système de carrés » possédait en elle-même, pour un initié de ce temps, un riche contenu herméneutique, associé aux valeurs possibles des carrés magiques que l'on pouvait former sur ces matrices.
La somme des aires des petits carrés vaut 13, tandis que l’aire du grand carré vaut 25 : valeurs qui correspondent aux centres des carrés magiques de Mars et Vénus (dans la Talismanie de Cornelius Agrippa), qui ont curieusement un rapport de moitié (13 / 25).
La symbolisme des amours de Mars et de Vénus, dont l'union adultère et clandestine, découverte par les olympiens, fut la cause du « rire inextinguible des dieux » pourrait sembler, - en raison de sa « trivialité » même, être un bon candidat à l'expression d'un « mystère » qui est celui de la Nature. Rappelons nous que, selon Empédocle, la nature universelle est bien conduite par cette force, autrement appelée Amour, qui, agissant entre eux comme un véritable tiers (bien qu'inapparent), « précipite » follement les sexes l'un contre l'autre.
Le couple adultère, surpris, est emprisonné dans un filet par Vulcain. Or, les carrés gnomoniques, qui forment la trame du rectangle de Fibonacci, sont classiquement qualifiés de "filets", pièges à poissons.
En ouvrant le carré de 5x5 (en vert dans le diagramme reproduit un peu plus bas) du côté où le rectangle est « sectionné », (en tant que structure susceptible de poursuivre sa croissance indéfinie), on peut reconnaître une forme qui évoque le symbole hermétique du LUX symbolisme d'une richesse telle que nous ne pouvons l'aborder ici (note 2)
Le symbole hermétique du LUX
éclaire la position de l'ange de la Melencolia de Dürer :
le bras droit en L, le bras gauche en U et les jambes croisées en X
Ces formes renvoient bien aux positions masculine et féminine : le L est anguleux et double (comme la raison masculine) et le U courbe et unaire (comme la jouissance féminine). Equerre et compas, qui résonnent avec les symboles hiérogamiques de la tradition hermétique chinoise, où le X est figuré par l'enlacement des "tentacules" serpentiformes. Ces remarques peuvent appuyer l'idée de différencier les 5 du 515 de Dante : en mâle et femelle, monade et dyade, intérieur et extérieur, ou autant de distinctions que l'on voudra (note 3).
Ajoutons enfin cette contribution poétique moderne à la tradition secrète du 515 : dans son roman Ulysses, James Joyce écrit ce palindrome en 11 lettres (5+1+5) :
Madam, I'm Adam

Le X forme la copule entre les lettres L et U,
indiquée ici par le croisement du VAV et du palindrome.
La réalisation de ce X sera le sujet des deux chapitres suivants.
III. LA JERUSALEM CELESTE - MONDE DU PALINDROME, DU RETOURNEMENT ET DU MIROIR - LE JARDIN D'EDEN - LA RELIGION DU LYS - YAKINTOS, AUTRE DISCIPLE D'APOLLON - LA DEESSE IRIS ET L'ARC EN CIEL

La Jérusalem Céleste
Plusieurs commentateurs ont identifié dans la troisième division du carré du Centaure, avec raison croyons-nous, le thème de la Jérusalem Céleste.
Dans l'Apocalypse, la Jérusalem Céleste est une cité éternelle descendue du ciel pour accueillir la communauté des élus du christ, ces 144 000 que l'on voit rassemblés, selon une répartition quadrangulaire, autour de l'Agneau du sacrifice, trônant au sommet du mont Sion.
En préambule, on pourra remarquer que le symbole ésotérique de la Jérusalem Céleste est, dans son essence même, placé sous le signe du miroir, et du retournement ; qui explique que, dans l'iconographie, sa représentation soit souvent caractérisée par une symétrie bilatérale, par la symétrie même du palindrome.
En effet, la Jérusalem Céleste est le reflet ou le miroir de la cité terrestre. Avec cette précision toutefois que, selon le principe « de Borella », qui veut que dans un symbole, ce soit toujours l'inférieur qui symbolise le supérieur, nous devons penser que, dans l'esprit des Templiers aussi, la Jérusalem terrestre n'était que le reflet ou la manifestation temporelle d'une cité éternelle, gouvernée par le Christ, dont l'existence avait en réalité infiniment plus d'importance
Ceci ne devant, en rien, occulter le fait que le sort de cette Jérusalem terrestre était, non seulement, la préoccupation majeure et quotidienne de l'ordre Templier, mais aussi sa raison d'être historique.
Dans la logique de cet engagement, il semble vraisemblable que nos templiers, en tant que moines-soldats dévolus à la défense de la Jérusalem temporelle, se sentaient appelés, par leur vocation même, à prendre place, au ciel, dans cette autre armée, éternelle, qui était celle des élus du Christ.
Le champ symbolique de la Jérusalem Céleste correspondait donc pour eux à ce qu'on entend par « le côté intérieur de la guerre ».
Plan carré de la cité, nombres 12 et 144
« La ville brillait d'un éclat semblable à celui d'une pierre précieuse, d'une pierre de jaspe transparente comme du cristal. Elle avait une très haute muraille, avec douze portes, et douze anges gardaient les portes. Sur les portes étaient inscrits les noms des douze tribus d'Israël. Il y avait trois portes de chaque côté : trois à l'est, trois au nord, trois au sud et trois à l'ouest. La muraille de la ville reposait sur douze pierres de fondation, sur lesquelles étaient inscrits les noms des douze apôtres de l'Agneau. »
« L'ange qui me parlait tenait une mesure, un roseau d'or, pour mesurer la ville, ses portes et sa muraille. La ville était carrée, sa longueur était égale à sa largeur. L'ange mesura la ville avec son roseau : douze mille unités de distance, elle était aussi large et haute que longue. Il mesura aussi la muraille : cent quarante-quatre coudées de hauteur, selon la mesure ordinaire qu'il utilisait. La muraille était construite en jaspe, et la ville elle-même était d'or pur, aussi clair que du verre. Les fondations de la muraille de la ville étaient ornées de toutes sortes de pierres précieuses: la première fondation était de jaspe, la deuxième de saphir, la troisième de calcédoine, la quatrième d'émeraude, la cinquième de sardonyx (onyx), la sixième de sardoine (cornaline) la septième de chrysolithe (peridot), la huitième de béryl (aigue-marine), la neuvième de topaze, la dixième de chrysoprase, la onzième d'hyacinthe (zircon brun) et la douzième d'améthyste. Les douze portes étaient douze perles; chaque porte était faite d'une seule perle. La place de la ville était d'or pur, transparent comme du verre. »
Dans ces lignes sont contenus les quelques éléments, rares, mais précis, qui gouvernent les représentations médiévales de la Jérusalem céleste. La ville est habituellement représentée suivant un plan carré et symétrique, avec 3 portes de chaque côté. Mais les portes peuvent être aussi des tours.
A Montsaunès, nous rencontrons une interprétation un peu différente, où à première vue il peut même paraître difficile de reconnaître les canons du genre.
Au lieu de 12 portes disposées le long de quatre murs, nous avons 4 fleurs de lys, disposées dans les quatre angles d'un carré, et porteuses de 12 pétales.
Nous nous demanderons plus loin quelle est la signification précise de ce symbole floral, mais, en préambule, on peut observer que cette symbolisation « végétale » pourra, dès l'abord, apparaître conforme à une autre tradition relative à la Jérusalem Céleste (non plus seulement chrétienne, mais aussi hébraïque), qui identifie précisément la Jérusalem Céleste au jardin d'Eden ; et cela, en vertu d'un principe assez universel du symbolisme ésotérique, selon lequel la fin (la Jérusalem Céleste), coïncide avec le commencement (le jardin d'Eden) ; l'omega avec l'alpha ; mais aussi la Terre (le jardin) avec le Ciel (la cité). Notons que dans ces traditions, le jardin d'Eden est décrit selon un plan qui a lui aussi la forme d'un carré, arrosé par quatre fleuves, etc.
La représentation de Montsaunès constitue donc une adaptation du genre, qui lui permet, dans le contexte, de porter des strates de signification supplémentaires. Ainsi, en situant les 12 « portes » (les 12 pétales) dans les angles du carré plutôt que sur les côtés, le plan de la cité adopte la structure du carré gnomonique, qui est non seulement celle du grand dessin le contenant (le carré du Centaure, dont il « réplique » ainsi endomorphiquement la séquence), mais qui est aussi le principe constructif du rectangle de Fibonacci, sujet de l'étape précédente.
Enfin, cette réinterprétation vise, selon nous, à une autre fin, plus importante encore. En polarisant une structure carrée sur ses angles, plutôt que sur ses côtés (sans même nous attarder à la tradition ésotérique bien nourrie qui identifie les « angles » aux « anges »), on attire l'attention sur une « cinquième » essence, coïncidant avec son centre, et que diverses traditions (dont la maçonnique) désignent comme le « mystère », ou « le 5 au centre du 4 ».
Dans l'Apocalypse, le plan carré de la cité céleste est bien polarisé autour d'un centre qui est le mont Sion, et l'Agneau du sacrifice ; tandis que, dans d'autres représentations de la cité, (comme à Montsaunès) ce centre peut être représenté par le Temple ou le tabernacle, sans incidence sur la signification profonde du symbole.
La fonction du retournement
Nous venons de voir que le dessin de la Jérusalem Céleste comportait de nombreux éléments de « reprise » ou de « récapitulation » des deux étapes qui le précèdent ; raison pour laquelle, pour nous aussi, une première récapitulation sera bienvenue.
La première étape - le lancer de flèche – symbolise le Fiat Lux, l'acte créateur qui donne le branle à un monde, et qui peut équivaloir à la production d'un « germe » ou d'une « graine » d'univers, susceptible de développement.
La deuxième étape, le rectangle de Fibonacci représente le développement indéfini d'un univers à partir de sa graine, et dans un rapport de rapprochement constant avec le principe pur (le nombre d'or) enfermé dans sa matrice.
Autrement dit le principe simple de croissance ou de procession.
La troisième étape représente « le retournement », ce rendez d'un univers avec lui même, qui fait que son expansion ne le conduit pas à se « dissiper » dans l'infini, mais comporte, dès le principe, une limite, au delà de laquelle il sera soumis à une contrainte inverse, une contrainte devant le reconduire à la simplicité, à l'unité de son principe.
La Jérusalem céleste et le monde du palindrome représentent donc l'instance de la « conversion », ou la loi du retour, car pour revenir au lieu d'où l'on provient, il est nécessaire de se retourner.
En n'oubliant pas là encore, le « principe de Mathieu » voulant que : « seul peut procéder ce qui est capable de se convertir ». Autrement dit « La Jérusalem Céleste » précède le rectangle de Fibonacci sur le plan de la conditionnalité.
Aux 12 portes de la cité correspondent explicitement, dans le texte de l'apocalypse, le 12 tribus d'Israël et les 12 disciples du Christ, autrement dit la synthèse de l'Ancien et du Nouveau testaments, et l'accomplissement complet de la prophétie. Mais le contexte cosmologique et zodiacal de notre peinture permet aussi, bien évidemment, d'associer à ces symboles de complétude, celui de l'achèvement des 12 mois de l'année.
Dans l'imaginaire templier, cette cité renvoie immanquablement à la mesure, par l'Ange, de sa muraille : « 144 coudées de hauteur ». Le nombre 144 étant le carré de 12, il amplifie, dans la dimension de la puissance, l'idée de plénitude déjà associée au nombre 12, en la réfléchissant en elle même, (opération qui peut être vue comme analogue à celle du miroir, du palindrome).
Mais il y a mieux. Le nombre 144 n'est pas seulement le 12ème nombre carré, pour parler en langue pythagoricienne, mais aussi le 12ème nombre de Fibonacci. Autrement dit, il correspond à une phase du développement du rectangle de Fibonacci, ultérieure à celle du rectangle vu précédemment (5x8), dans laquelle le plus grand côté est formé de deux carrés de, respectivement, 55 et 89 de coté.
On peut donc penser que ce rectangle correspond à une seconde phase de plénitude, ou de complétude. Sur le plan symbolique, cette assimilation a pour effet d'énoncer clairement que « le rectangle de Fibonacci » et « la Jérusalem Céleste » ne sont fondamentalement qu'une même réalité, envisagée à deux moments différents de son développement, comme l'illustre leur quadrature de phase.

Les nombres 8 et 144, qui correspondent aux longueurs de ces deux rectangles, sont respectivement les 6ème et 12ème nombres de Fibonacci, ce qui les place ordinalement dans un rapport d'octave.
Le 5 alternant et le 9 conservant
A présent, observons que cette Jérusalem Céleste est bordée, à droite et à gauche, par une frise de pavés mosaïques dont la hauteur totale est de 14 pavés, répartis en 9 + 5 (note 4).
14 évoque naturellement une mi-temps du mois lunaire, pleine ou nouvelle lune (le cycle par excellence en raison de la netteté de ses phases) ; de la même manière que les solstices délimitent les mi-temps de l'année.C'est aussi un nombre que la tradition chrétienne associe aux souffrances du Christ, puisqu'il définit la lune pascale, et les quatorze stations du chemin de croix.
Si l'on décompose la « hauteur » totale en deux parties, haute et basse, correspondant aux cellules abritant les lys, on obtient pour ces pavés mosaïques le décompte suivant :
5 5
(9 & 9) (9 & 9)
Dans le registre supérieur, on peut lire une référence à la sacralité du nombre 5, dont on a décrit précédemment la qualité « alternante » fondamentale (principe de l'Autre).
Dans le registre inférieur, l'accent est mis sur la sacralité du nombre 9, qui représente le principe féminin de « conservation » (principe du Même), qui est sur le plan métaphysique la conservation de l'origine.
Eu égard aux neuf symboles primitifs par lesquels se manifeste la Décade, ces deux nombres reflètent l'adage hermétique qui veut que « tout s'oppose par les milieux (5) et se rejoigne par les extrêmes (9) ».
Y a-t-il un rapport avec le carré de la Jérusalem ?
Si l'on fait la somme de chaque ligne, on obtient :
5 + 5 = 10
(9 + 9) + (9 + 9) = 36
D'un point de vue pythagoricien, ces nombres entretiennent des rapports étroits, puisque :
- 10 et 36 sont respectivement les 4ème et 8ème nombres triangulaires.
- le premier est appelé tétractys : 1+2+3+4 ; et le second double tétractys : (1+3+5+7) + (2+4+6+8)
- 4 est le premier carré (2²) et 8 est le premier cube (2³). Ces deux nombres étant en outre dans le rapport d'octave, homologue au rapport Mars/Vénus.
On pourrait alors, assez naturellement, représenter les registres inférieur et supérieur par deux triangles, dont les polarités seraient inverses l'une de l'autre.
10

-----------------------------------------------

36
Idée dont on trouve une illustration dans Les Dialogues avec l'Ange :

« Deux triangles s’approchant l’un de l’autre dans une attraction mutuelle irrésistible.
Ils étaient reliés par un jaillissement d’éclairs jusqu’à ce que leur union soit totale. »
Ces pavages latéraux indiqueraient ainsi une « formation » de la Jérusalem, par union des triangles (point qui sera repris plus loin), en accord avec l'enseignement des loges compagnonniques, qui tiennent le triangle pour un intermédiaire obligé dans la résolution graphique de la quadrature du cercle.
Si l'on interprète le triangle supérieur dans sa fonction de tétrade, on remarque que 4 x 36 = 144 (opération qui reproduit la partition quadrangulaire de "l'armée des élus"); si on l'interprète comme décade, on note que 10 x 36 = 360 (nombre qui peut renvoyer à la plénitude du cercle, comme à celle de l'année).
Un autre aspect de la qualité théophanique du nombre 144 peut être illustré à partir de la séquence harmonique 6-8-9-12 à laquelle Nicomaque de Gérase prête les qualificatifs de médiété parfaite et d'harmonie, du fait qu'elle renferme les rapports des 3 médiétés, puisqu'en effet 144 = 6x12 + 8x9.
Souvenons-nous enfin que la mesure des 144 coudées avait mis en évidence la séquence de Fibonacci 55-89-144. Or, de même que le 144 croise la série de Fibonacci avec celle des nombres carrés, le nombre 55 croise cette série avec celle des nombres triangles... faisant écho à cette alliance entre le triangle et le carré. (note 5).

On peut d'abord voir une illustration très générale du principe qui nous occupe ici dans la relation mathématique liant les deux branches latérales de cette structure, en vertu de laquelle : "Tout nombre carré supérieur à 1 est la somme de deux nombres triangulaires successifs".
Le nombre 55, palindrome lisible à même la peinture, souligne quant à lui la présence du nombre 11 et de ses multiples, au premier rang desquels le 99 en vertu des remarques précédentes ("le dernier est encore le premier") (note 6)
Les nombres 11 et 99 représentent l'instance du centre qui est précisément celle qui « retourne en conservant », ou « conserve en retournant »... et dont la nécessité logique est au fond analogue à celle contenue dans le principe de Mathieu : « Seul peut procéder ce qui est capable de se convertir ».
La religion du lys : Cantique des cantiques
Au terme de ces considérations sur la composition de la Jérusalem Céleste et son symbolisme arithmétique, il est temps de nous interroger sur la signification du lys, qui en est d'une certaine manière l'élément principal, dans la symbolique templière.
Que représentent ces fleurs de lys? Que savons-nous au juste de ce symbole?
Le Cantique des cantiques est considéré comme un chant spirituel qui exploite, jusqu'aux limites de l'indécision et du vertige, l'analogie entre l'union charnelle de l'homme et de la femme, et l'union spirituelle de l'âme avec Dieu. Toutefois, une attention superficielle à la composante romanesque de ce chant fait apparaître un autre sujet principal, omniprésent, envahissant, qui est la ville de Jérusalem, qui fournit le cadre à la fois « anecdotique » (l'errance alternée des amants en quête l'un de l'autre dans la ville, leurs points de « rendez vous » en différents lieux de la cité), et en quelque sorte « métaphysique », dans la mesure où le personnage de « la bien-aimée » est constamment présenté comme la quintessenciation d'une entité plus large, et qui l'accompagne partout, et qui est celle des « filles de Jérusalem ». La bien-aimée est une fleur au milieu du « champ de fleurs » que forment les filles de Jérusalem.
Je suis noire, mais belle,
filles de Jérusalem,
comme les tentes de Cédar,
comme les pavillons de Salomon
et plus loin :
Je suis le narcisse de Saron,
le lis des vallées -
Tel un lis parmi les épines,
telle ma compagne parmi les filles
Et dans cette errance, dans ce tâtonnement aveugle des amants en quête l'un de l'autre dans le labyrinthe de la Ville, on remarque ceci :
Sur ma couche, durant les nuits,
j'ai cherché l'aimé de mon âme,
je l'ai cherché et ne l'ai point trouvé !
Les amants du Cantique se poursuivent, ou se cherchent, sur deux champs différents et parallèles, mais qui coïncident d'une certaine manière, qui sont le champ de la ville et le champ du Lit, sanctuaire de l'union amoureuse.
Et la bien aimée, qui est le lis, l'ornement de la ville, est aussi l'ornement du lit.
Mon bien aimé est descendu à son jardin
vers les parterres des baumiers,
pour mener paître parmi les jardins
et pour cueillir des lis.
Moi, je suis à mon bien-aimé
et mon bien aimé est à moi,
lui qui mène paître parmi les lis.
Sans occulter en aucune façon la crudité sexuelle de la formule : « Mon bien-aimé est descendu dans son jardin », nous voyons ainsi coïncider, par transitivité, « la Jérusalem » et « le lit » qui forment le double cadre symbolique du cantique des cantiques, avec un « jardin » qui rappelle, là encore, l'éternité de la condition édénique et du paradis terrestre.
Plus loin encore, la nature nettement « territoriale » de cette quête tâtonnante, de cette exploration par l'amant des mystères du jardin, en quête de lis, se précise encore un peu plus :
Les contours de tes hanches
sont comme des colliers
œuvre des mains d'un artiste ;
ton nombril est un calice arrondi
où ne manque pas le vin épicé,
ton ventre est un tas de froment entouré de lis
Alors qu'un peu plus tôt, la bien-aimée elle-même disait de son bien aimé :
Ses lèvres sont des lis.
Nous constatons ainsi que, dans l'Ancien testament, la religion du lis est avant tout une religion du lit, de l'union amoureuse, qui a pour cadre la ville de Jérusalem, et célèbre un mystère qui, pour le contenu, ne diffère pas grandement de celui des noces de Mars et de Vénus, que l'on a vu se développer dans le symbolisme arithmétique du rectangle de Fibonacci.
Ce contexte identifie clairement la force d'Amour comme étant, essentiellement, identique à la puissance du « retournement », ou de la « conversion » que symbolisent, dans le contexte de notre peinture : la Jérusalem céleste et son principe « palindrome » (note 7)
La religion du lys : Saint Bernard
On sait que Bernard, qui prêcha à Vézelay la deuxième croisade, assuma aussi, une bonne partie de sa vie, le rôle de pasteur et de guide spirituel de l'église templière.
Bernard est aussi l'auteur d'un cycle de 86 sermons sur le Cantique des cantiques, dont la rédaction s'étend sur la majeure partie de sa vie pastorale, et qui forment quantitativement aussi la partie la plus importante de son œuvre spirituelle.
Dans la conduite de son commentaire, Bernard privilégie l'interprétation traditionnelle qui voit, dans l'union de l'amant et de l'aimée, la transposition du lien entre le Christ et l'église, ou entre l'âme et Dieu.
Le thème et l'action du Cantique des cantiques sont donc repris chez lui dans une perspective résolument chrétienne, (qui sera reprise par Dante dans son exégèse prophétique de l'Apocalypse), dans laquelle la « fiancée », la femme, représente l'Eglise, épouse du Christ ; perspective dans laquelle, par voie de conséquence, le contexte symbolique de « La Jérusalem » se confond, eschatologiquement, avec celui de l'église chrétienne.
Précisons que, d'un point de vue chrétien, cette transposition semble parfaitement légitime et fondée, puisqu'elle s'appuie continuellement, chez l'un comme l'autre de ces auteurs, sur le texte de l'Apocalypse.
Une surprise nous attend néanmoins au début de son sermon 47ème, où Bernard attribue, - au rebours de ce que semble être la lecture habituelle - à l'Epoux, et non à l'Epouse la parole : Je suis la fleur des champs et le lis des vallées. Il y voit une réplique de l'Epoux à la prétention formulée plus tôt par l'Epouse, selon laquelle : « Ma couche est semée de fleurs » Là où déjà, on pouvait se contenter de lire « ma couche est un tapis de verdure ». « Pour qu'elle ne s'attribue pas, écrit Bernard, les fleurs qui paraient son lit et sa chambre, l'Epoux dit qu'il est lui-même la fleur des champs. »
Bernard semble par ce forçage vouloir imposer un ultime « retournement » à « la force de retournement » elle-même ; en vertu duquel « même les fleurs des champs ne naissent que par la vertu de Dieu ». Et dans ces conditions, le fidèle auquel s'adresse son sermon, n'est pas invité à s'identifier au bien-aimé, à l'Epoux, mais à la bien-aimée qui est sa fiancée, l'âme, ou encore, l'Eglise, dont il est un membre et une partie, à la manière de l'une d'entre les « filles de Jérusalem ».
*
Un auteur très estimé considère l'art (folklorique) des allemands de Pennsylvanie comme la survivance d'une tradition mystique remontant à Saint Bernard et Dante (John Joseph Stoudt, Consider the lilies how they grow)
L'élément frappant dans ces œuvres, outre l'omniprésence de symboles comme le lis, la colombe, le cœur, ou l'arbre de vie, est bien-sûr la symétrie bilatérale, symétrie en « palindrome » qui gouverne la composition de la plupart.
Le terme « lis » a une extension assez large qui ne saurait prétendre à la précision botanique. Ainsi, si les lis de Montsaunès ressemblent bien à des lis ou des iris « ordinaires », le lis des vallées de Saint Bernard désignerait plutôt en principe le muguet (autrefois classé dans les liliacées), tandis que les lis de Pennsylvanie seraient plutôt des tulipes (qui elles appartiennent bien aux liliacées).
Hyacinthe, un autre disciple d'Apollon
Hyacinthe était le fils d'un roi de Sparte, aimé en même temps d'Apollon, et d'un vent, Zéphyr ou Borée. Apollon lui apprend à lancer le disque, mais le vent jaloux lui fait revenir dans la tempe, et de son sang naissent des fleurs qu'on appelle, d'après le nom du jeune homme, des huákinthoi, dont les pétales portent l'initiale du jeune homme, Y, ou selon une autre version, le mot ΑΙ, cri de lamentation d'Apollon.

La mort d'Hyacinthe
Jean Broc (1801)
On apprend sur Wikipédia que ces fleurs « ne sont probablement pas des jacinthes, mais plutôt des iris (...) Déjà considéré comme sacré par les Égyptiens, l'iris est devenu, sous le nom héraldique de fleur de lys, le symbole de la royauté en France ».
Et l'on peut s'informer plus loin que le nom fleur de lys « apparaît sous le règne de Louis VII, dans Érec et Énide, peu après 1160, et que ce terme est phonétiquement identique, en tout cas très proche de 'Flor de Loys' (fleur du roi Louis) ». Louis VII avait en fait adopté l'iris des marais pour blason, mais l'assonance entre 'Flor de Loys' (l'iris) et 'Flor de Lys' a perpétué une équivoque historique.
Une vingtaine d'années séparent la construction de l'église de Montsaunès, de la rédaction d'Erec et Enide. On surprend donc ici l'émergence historique, dans l'iconographie, puis dans la littérature, d'un symbole appelé à désigner, plus qu'aucun autre, la sacralité de la royauté française.
Si nous reprenons maintenant la séquence du centaure sous l'angle de la religion de Pythagore, nous remarquons une relation d'opposition diagonale entre le centaure Chiron, piqueur ou flécheur d'Apollon, et Yakintos, l'homme lys, jeune homme aimé d'Apollon qui sera la victime sacrificielle de cet amour. Les figures de Chiron et de Yakintos se disposent autour d'Apollon dans ces rôles antagonistes, qui sont ceux du sacrificateur et du sacrifié, et qui, transposés sur le plan de la philosophie de la nature, pourraient aussi être compris comme ceux de « l'agent » et du « patient », de « l'actionneur » et de « l'actionné »
La déesse Iris et l'arc en ciel
Une tradition fait du vent Zéphyr, possible meurtrier de Yakintos, l'époux de la déesse Iris (note 8) messagère des dieux, qui est une sorte de pendant féminin d'Hermès, attachée à Héra comme Hermès l'est à Zeus.
On la représente sous la figure d'une gracieuse jeune fille, avec des ailes brillantes de toutes les couleurs réunies. Les poètes prétendaient que l'arc-en-ciel était la trace du pied d'Iris descendant rapidement de l'Olympe vers la terre pour porter un message ; c'est pourquoi on la représente le plus souvent avec un arc-en-ciel. C'est la déesse de l'arc-en-ciel.
Dans le dessin de la Jérusalem Céleste, le centre de la composition est occupé par une arche, qui semble former la "copule", le lien qui scelle son caractère palindromique. La voûte est divisée en plusieurs tronçons, qui peuvent évoquer la division des couleurs de l'arc en ciel (note 9)
Le symbolisme de l'arc en ciel fusionne donc ici avec celui de la porte. Le sujet principal de la peinture étant la porte du solstice, on comprend qu'une assimilation naturelle s'effectue entre cette porte cosmologique et temporelle, et la porte "spatiale" du Temple de Jérusalem, donnant accès à son "centre", à son "saint des saints".
Sur le plan symbolique enfin, nous verrons plus loin que le thème de l'irisation, du déploiement des couleurs de l'arc en ciel, (traditionnellement associées au nombre 7), prépare un thème qui sera complètement développé dans la dernière partie du carré du centaure, qui est celui de l'Illumination et de l'Ignition, symbolisé par le chrisme, et associé cette fois au déploiement des directions de l'espace, qui sont elles aussi au nombre de 7.
Le symbole pythagoricien du Y
"Les pétales de la fleur portent l'initiale du jeune homme, Υ"
Dans le mythe d'Hyacinthe, la lettre Y, en plus d'imposer une représentation ternaire de la fleur de lys qui restera "canonique", représente l'initiale du héros dont le sang a donné naissance à la fleur.
Or, indépendamment de ces données mythologiques, le Y est symbole très bien connu, dont l'origine est donnée partout comme pythagoricienne, bien que sa fortune ait été beaucoup plus large, et qui signifie "la croisée des chemins". Dans la version commune et popularisée, ce symbole revêt principalement une connotation morale, et représente "la voie droite et la voie gauche", ou encore "les voies du Bien et du Mal"; mais on peut penser que ce symbole avait à l'origine une extension moins limitée.
En effet, d'un point de vue géométrique, le Y est analogue au trépied joignant les trois sommets de la tétractys à son centre. Pour obtenir les 6 autres points de la tétractys, le trépied doit être complété par un hexagone de même centre. Et relativement à cet hexagone, figure traditionnellement assimilée au cercle, le trépied fait figure de structure "axiale", sinon même "polaire", en ce qu'elle émane entièrement d'une partie d'elle-même, qui est son centre de géométrie.

« La onzième était d'hyacinthe »
Si le mythe grec d'Hyacinthe est bien associé à l'étymologie d'un nom de fleur, l'hyacinthe de la Jérusalem céleste désigne, dans l'Apocalypse, une pierre précieuse, dont on pourra malgré tout s'étonner qu'elle fournisse le matériau de la onzième pierre de fondation de la cité céleste : autrement dit la pierre du palindrome.
Le retournement du cœur
Si l'on s'en tient à la famille des iris, la représentation commune de la fleur de lis correspond à une réalité botanique, au moins schématique, puisque de nombreux iris présentent une composition hexagonale, formée de 3 + 3 pétales, disposés en "sceau de Salomon".
Il est impossible, ici, de ne pas évoquer au moins brièvement un symbolisme assez universel, abordé notamment par René Guénon, qui fait du triangle inversé (pointe en bas)
- d'une part, un symbole du cœur, - la symbolisation la plus courante du cœur pouvant aisément être inscrite ou circonscrite à la figure d'un triangle pointe en bas ;
- d'autre part un symbole de la caverne initiatique. "La caverne du cœur" étant une expression traditionnelle qui renvoie expressément à l'équivalence, ou à la coïncidence de ces deux aspects d'un même symbole
Les deux ententes possibles de ce symbole sont elles-mêmes reliées par des liens complexes ; puisque chacune se rattache, de façon indépendante, au symbolisme plus général du centre : le cœur représentant dans cette conception le centre de l'individualité humaine, tandis que la caverne initiatique représente, quant à elle, le centre du monde.
Ce symbolisme donne lieu à des développements qui ne peuvent qu'être effleurés ici. Dans l'un d'eux, le symbole de la caverne initiatique se combine avec celui de la montagne, elle même comprise comme une expression symbolique de "l'axe du monde". Ici le triangle inversé représentant la caverne demeure enfermé dans les limites du grand triangle "pointe en haut", qui représente la montagne. La caverne se situe au cœur de la montagne, et son entrée sur le flanc de celle-ci.
Dans une autre application de ce symbolisme, le triangle du cœur se combine avec un triangle inverse pour former la figure bien connue du "sceau de Salomon", mais selon une interprétation bien précise où ces deux triangles n'ont pas exactement la même valeur, puisque l'un deux, "le triangle du cœur" (qui correspond dans le symbolisme précédent au triangle "intérieur") est donné comme antérieur à l'autre. La figure du sceau de Salomon ne représente pas, alors, une réalité statique, mais bien une opération, qui est celle du retournement du cœur, expression que l'on peut considérer comme équivalente à la notion de "conversion".
2
1
Il est permis de voir là une illustration particulièrement frappante de l'accord des doctrines traditionnelles, ou si l'on préfère, de la consistance et de la cohérence intrinsèque des conceptions métaphysiques sur lesquelles repose la science des symboles.
En effet, notre enquête nous a montré que le symbole de la Jérusalem céleste était relié par des liens multiples à l'instance du cœur, d'une part, mais aussi à l'opération particulière de la conversion.
Au sein de ce contexte biblique, le symbole du lys a pu d'abord nous apparaître comme un intrus, un invité surprise, bien que chargé d'un très riche héritage traditionnel, aussi bien dans la mythologie que dans les écritures saintes.
Or, rétrospectivement, une attention simple à la géométrie hexagonale de la fleur de lis permet de constater que ce symbole pouvait lui-même renvoyer directement - sans le secours d'aucun autre - aux mêmes idées.
INTERMEDE : LE RAPPORT 11/12 - VERS LA PLENITUDE
Il convient de s'arrêter sur un détail de notre peinture, dont la netteté et la précision excluent toute possibilité qu'il puisse être hasardeux.
A la jonction du quadrilatère de la Jérusalem Céleste et de celui du chrisme, une frise mosaïque permet de définir rigoureusement le rapport arithmétique entre les côtés de ces figures : 11/12
Un registre supérieur de longueur 12 surplombe un registre inférieur de longueur 11.
Ce rapport est marqué avec une insistance telle qu'il ne peut pas être fortuit, compte tenu du déséquilibre gratuit qu'il introduit dans la composition.
En première analyse, ce rapport est susceptible d'une interprétation zodiacale. Dans une représentation « capri-axée » de la roue zodiacale, où le Capricorne occuperait la douzième heure du cadran, et le sagittaire la onzième, le rapport de « conjonction » entre les mois 11 et 12 évoque précisément l'événement qui fait le sujet de notre peinture : le solstice d'hiver.
Mais le rapport 11/12 est aussi le rapport qu'entretient, du point de vue gnomonique, le solide de Dürer à son rhomboèdre associé. (22 éléments pour le solide, 24 pour le rhomboèdre) En rappelant, pour mémoire, qu'un solide de Dürer est un rhomboèdre tronqué.
Ce rapport 11/12 est très typique et personnalisé, autant que l'octave ou la quinte. Quand on l'a vu une fois, (dans le solide de Dürer) on ne peut plus l'oublier ; et il signifie clairement le rapport (qui peut évidemment être dynamique) entre un état "tronqué" et un état de plénitude. (note 10)
IV. CHRISME : LE MONDE DE LA PLENITUDE – LE TEMPS DE L'ACCOMPLISSEMENT – LA LIBERATION DU POINT OU DU FEU CENTRAL

Le chrisme est l'élément principal de la dernière partie du carré du Centaure.
Même si ce symbole est loin d'être un inconnu, il ne sera peut-être pas inutile d'en reprendre brièvement l'analyse d'un point de vue qui est à la fois pythagoricien et chrétien, puisque l'apôtre Paul, qui en est l'exégète, s'y affirme ici sans équivoque en disciple de Pythagore.
La figure du chrisme tridimensionnel représente le déploiement des 6 directions de l'espace à partir du point central dont elles émanent, et qui les contient toutes en puissance. Les directions ou « rayons » sont parfois comptées comme 7 , lorsque le point central est considéré comme une « direction » ou une « polarité » distincte des six autres. Sous cette forme pour ainsi dire synthétique ou « squelettique », le symbole du chrisme exprime déjà la complétude des dimensions de l'espace, puisque chacun des trois « brins » dont il se compose correspond à l'une de ces dimensions.
Du point de vue topologique, le chrisme est analogue à la monade pythagoricienne, dont la fonction, quant à elle, est de représenter sous forme synthétique les quatre différents états possibles de la monade, correspondant aux quatre objets élémentaires de la géométrie que sont : le point, le segment, le disque et la boule. (Et cette similitude est encore renforcée lorsque, comme à Montsaunès, le chrisme est inscrit dans un cercle.)
Or nous sommes bien contraints de constater que, dans la doctrine paulinienne du plérôme (de la plénitude) c'est bien la lecture pythagoricienne, la lecture quaternaire de ce symbole qui est favorisée, et non la lecture « ternaire » ou « trinitaire » qu'on pourrait facilement attendre ici, en liaison avec les trois dimensions ou les trois « brins » du chrisme.
"Ainsi, vous recevrez la force de comprendre, avec tous les saints, ce qu'est la Largeur, la Longueur, la Hauteur et la Profondeur, vous connaîtrez l'amour du Christ qui surpasse toute connaissance, et vous entrerez par votre plénitude dans toute la Plénitude de Dieu." (Éphésiens, III, 19)
Dans cette formulation paulinienne de la doctrine, les trois premières dimensions (largeur, longueur, hauteur) correspondent manifestement à celles qui caractérisent un objet tridimensionnel tel que le cube (équivalentes aux trois brins d'un chrisme), tandis que la quatrième, "profondeur", correspond à la dimension du point. Autrement dit, ce qui est premier dans l'ordre constructif de la géométrie - le point - se révèle "dernier", au sens de plus éminent et essentiel, sur l'échelle de la plénitude.
Du point de vue pythagoricien que nous avons tenté de développer dans ces lignes, on admettra en tous cas que la situation du chrisme, symbole de la plénitude, sur la quatrième et dernière case du carré gnomonique du centaure, apparaît totalement légitime et fondée, puisque cette étape correspond au développement complet de la monade.

Correspondance symbolique avec le 515
On a vu, dans le cadre du symbolisme de la chasse spirituelle et du cerf dix cors, que la figure messianique du 515 se présentait souvent comme « réplication » de celle du Christ.
Ces deux figures communiquent aussi sur le plan du symbole. Lima de Freitas remarque que, par un jeu sur la graphie romaine des chiffres 5, 1, 5 (VIV), ces trois nombres peuvent s'assembler pour former un chrisme que les touches du clavier permettent de représenter :
>l<
Réapparition du nombre 40
Le nombre de pavés entourant le chrisme est de 40, répartis en 20 blancs et 20 noirs.
D'un point de vue symbolique, le nombre 40 qui, dans le rectangle de Fibonnaci correspondait à l'aire, et donc à « l'intérieur » du rectangle, se retrouve « à l'extérieur », puisqu'il correspond maintenant à son périmètre.
Ce rapport nous indique qu'entre les deux situations, la réalité s'est « retournée » ou plus exactement « retroussée », de telle manière que « le dedans est passé au dehors et le dehors au dedans » ; ce qui cohérent avec l'opération qui a eu lieu dans l'intervalle, et la traversée du monde du palindrome, dont la fonction est précisément d'opérer un « retournement ».
Examinons à présent le dallage situé sous le chrisme.
Si on considère, dans le rectangle de Fibonacci, le seul pavé de 3x3, et la manière dont il est "hachuré", on constate que sa structure est analogue à celle du pavage en losange situé sous le chrisme. Ce carré de 3x3 pourrait être colorisé avec des triangles noirs sur les bords, pour renforcer l'analogie. (note 11)

C'est la même structure, sauf que celle qui est sous le chrisme correspondrait à un carré gnomonique de rang 4, et non de rang 3. De ce point de vue précis le passage de "Fibonacci" à "chrisme" se traduit par un "développement" de 3 à 4 (note 12)
A partir d'un carré de 4x4, le pavage du chrisme devient entièrement paramétrable et "discrétisable", la décomposition la plus complète aboutissant à 64 triangles. Sur la base de cette "réduction à l'atome", on peut faire différents comptages, les triangles-atomes de la zone blanche pouvant de différentes manières s'assembler en carrés, mais on connait déjà le poids total. Chacun des 16 carrés se divisant en 4 triangles, on a une décomposition atomistique complète qui permet d'attribuer aux petits triangles noirs la valeur 1.
La zone noire vaut alors 12 x 1 = 12
Tandis que la zone blanche vaut 64 - 12 = 52
On peut se demander pourquoi cette division en 52 blancs et 12 noirs.
Le noir pourrait être interprété comme le négatif du blanc. En attribuant aux triangles de la zone blanche la valeur 1, et à ceux de la zone noire la valeur -1, on obtient la soustraction :
52 - 12 = 40
Soit une troisième façon d'engendrer le nombre 40, après le rectangle de Fibonacci (5x8), et la frise du chrisme, où le chemin à 40 dalles est engendré par croisement du 10 et du 12.
Nous avons déjà remarqué qu'un sujet récurrent de la peinture, concerne la sacralité du nombre 40 ; les considérations calendaires formulées par Aliboron sur des bases à la fois celtiques et pythagoriciennes, pourraient montrer que ce nombre n'est pas sans rapport avec le sujet central de la peinture, qui est le décompte ou « l'achèvement » des jours de l'année.
Mais une autre méthode d'interprétation de cette division 52 - 12 du pavage pourrait, quant à elle, s'accorder de façon encore plus directe avec le thème local de la plénitude de l'année, puisqu'en effet :Un an = 12 mois ou 52 semaines
Nous verrons plus loin, par la comparaison avec les autels de l'Agnichayana, dans lesquels la construction du pavage équivaut au "remplissement" du temps de l'année, qu'une telle hypothèse n'a rien d'invraisemblable.
Dernière remarque, la répartition des pavés noirs et blancs dessine une croix de Saint André, dont on doit remarquer qu'elle comporte une asymétrie – asymétrie qui ne peut passer pour une inattention puisqu'elle est reproduite, identiquement, dans une autre partie de l'église. Pour que la symétrie soit rigoureusement respectée, l'un des pavés blancs « surnuméraires » qui occupent les angles du carré - celui en bas à gauche - aurait dû être placé à l'inverse de ce que l'on voit.Une telle anomalie vise à marquer, au sein de la tétrade des « rayons » de la tétractys, une asymétrie 1- 3, une différence qualitative entre le « point central » de la monade, ou le point origine de la tétractys, et les « rayons » correspondants aux dimensions euclidiennes de l'espace.
Et on peut voir là la répétition d'un motif qui était déjà explicite dans la répartition des flèches du centaure : 3 flèches rangées dans son carquois, et la quatrième bandée à son arc ; ou encore, dans les 4 fleurs de lys de la Jérusalem Céleste, dont l'une, en haut et à droite, arbore des "volutes" que n'ont pas les trois autres.
V. LE CARRE GNOMONIQUE - LE MYSTERE AU CENTRE DU QUATRE - L'AUTEL D'AGNI
Nos remarques nous ont convaincu que nous avions affaire, dans le carré du centaure, à une séquence temporellement ordonnée, dans laquelle les rapports entre étapes sont indiqués de façon très appuyée. Les sabots arrières du centaure détachent l'axe de division du rectangle Mars/Venus ; un trait excessivement marqué jointe par le bas ce rectangle au "carré" de la Jérusalem, temple du palindrome ; enfin le rapport 11/12 qualifie le rapport final "d'accession à la complétude".
Il est temps de nous demander : quel peut être le sens de tout cela ?
Y a-t-il, dans le fait d'assembler un ensemble aussi considérable de symboles dans une machine, un système symbolique contenant, au sein duquel ils se répondent et s'éclairent les uns les autres (système en lui-même remarquable par sa simplicité) – y a-t-il dans un tel ouvrage une dimension de réalisation pratique et rituelle ?
Dans son ouvrage : Gnomon, une enquête sur le nombre, Paolo Zellini a relevé avec beaucoup de pertinence l'analogie qui existe entre la structure du carré gnomonique et la construction de l'autel d'Agni, dans le rituel de l'Agnichayana. (note 13)
Et nous ne pouvons pas, ici, manquer de nous souvenir qu'une étymologie très ancienne, validée par René Guénon, apparente la racine sanskrite du nom Agni, non seulement au latin Agnus (agneau), mais aussi à la racine latine Ignis, qui signifie le feu.
Rappelons-nous que, dans le contexte de l'Apocalypse, la répartition en carré de l'armée des élus (qui se disposent dans l'espace selon les 4 directions ou les 4 vents), n'a pas d'autre fonction que de servir de « support » ou de soutènement au « mystère » qui s'accomplit au centre du carré, dans le sacrifice de l'Agneau mystique.
L'Agneau qui, dans notre représentation de la Jérusalem Céleste, est l'élément manquant (par rapport aux représentations traditionnelles), remplacé une Arche symbolisant l'entrée du "Temple" ; pourrait bien ainsi, par une sorte de procédé elliptique, être désigné comme l'élément ou le personnage principal de la quatrième partie du carré du centaure (ce qui au point de vue théologique ne souffre d'aucune contestation, puisque le chrisme et l'Agneau sont bel et bien l'un comme l'autre des symboles du Christ).
Le développement final du chrisme, associée à la « matérialisation » ou à la libération de son point central, peut également être compris comme l'accomplissement, ou la réussite, d'un processus d'Ignition, ou d'illumination.
Ce qui viendrait également au soutien au fait que les fêtes solsticiales associées aux deux Saint Jean soient, l'une comme l'autre, dans les traditions folkloriques, associées au feu et à la lumière.
D'un point de vue pythagoricien, nous n'avons jamais eu trop de doute sur le fait que le carré gnomonique, dans lequel se trouve enfermée, sous la forme la plus simple et évidente, la relation logique du gnomon, n'ait été le support d'exercices rituels, du même genre que ceux que l'on a pu identifier pour la tétractys, le pentagramme ou le 4 de chiffre.
La cérémonie védique de l'Agnichayana
Une des plus importantes cérémonies du védisme en ce qui concerne le culte du feu, l'Agnichayana, consiste à construire religieusement l'autel pour le feu.
Les principes "architectoniques" régissant les autels sont les mêmes que ceux qui régissent la construction des maisons, ou des temples. Tous sont très explicitement des représentations du monde, du cosmos, comme la grotte d'Ithaque. Quant au rituel de construction de l'autel, qui dure 12 jours, il consiste, selon ses pratiquants, à "reproduire à l'identique le processus de la création du monde".
Il existe de multiples modèles d'autels. L'un des plus pratiqués nécessite exactement 10800 briques.
Il y une double assimilation de l'autel au cosmos, d'une part, et à l'année de l'autre : dualité dans laquelle on retrouve exactement la valeur spatio-temporelle du "rendez-vous solsticial". L'année et le cosmos, dans le rituel, se "complètent" ou se remplissent donc "en même temps".
Ainsi les 10800 briques correspondent à une division de l'année égale à 48 minutes (muhurta), en se basant sur une année de 360 jours. (48 x 10800 min = 360 jours) (note 14)
Règle : tous les autels sans exception ont 5 étages de hauteur, et le 5 est prépondérant ailleurs dans les proportions.
La composition des pavages est bien identique à celle de Montsaunès, savoir :
- des carrés
- des triangles rectangles qui sont des demis carrés
- des triangles rectangles qui sont des quarts de carrés
Ancient geometry. Boys working on model of bird-shaped fire altar in an Agnicayana ritual.
D'un point de vue pythagoricien, cette caractéristique est intéressante en ce que toute surface sera convertible en "carré" et quantifiable comme du gnomon pur. Par exemple : si le carré vaut 4, le grand triangle vaut 2 (ou un carré long) et le petit triangle vaut "atome" ou graine de valeur 1.
Si la plupart des autels adoptent les formes d'animaux (oiseaux, tortues), il existe des autels de forme carrée. Sans nous hasarder à des hypothèses d'antériorité, on peut penser que ces autels carrés représentaient une forme "épurée" ou "matricielle", relativement aux formes plus figuratives.
L'un de ces autels carrés, appelé Caturascit, se présente ainsi :

A comparer avec le pavage en croix sous le chrisme, à Montsaunès.
Alors que le pavage de Montsaunès a pour base un carré gnomonique de rang 4, le Caturascit a pour base un carré gnomonique de rang 10. Les deux pavages ont en commun d'être structurés par une croix de Saint-André, dont la fonction la plus évidente est de conduire l'énergie du carré des angles vers son centre.
Enfin, sur le fond des choses, le concept de rayonnement peut gloser, de façon assez juste, l'opération du chrisme, le caractère opératoire de ce symbole; mais le concept d'ignition nous semble l'exprimer de façon tout aussi profonde, d'autant qu'Agni, lui aussi, est porteur de sept rayons.
Jean Herbert : « Le nombre 7 a une grande importance pour Agni qui a sept flammes, 7 langues, 7 rayons, 7 pieds de même qu'il y a 7 feux, 7 sacrificateurs, 7 porteurs d'holocaustes et 7 hotracas qui font naître. »
Le chrisme est posé sur le pavage - comme le feu est allumé sur l'autel d'Agni.
Enfin - ô surprise - la cérémonie de l'Agnichayana se concluait autrefois par le sacrifice sanglant, non d'un agneau - mais d'une chèvre.
Ces remarques laissent pour l'instant entière la question de savoir pourquoi, ou comment, un ordre de chevalerie religieux du XIIe siècle pouvait détenir des conceptions doctrinales, et peut-être liturgiques, similaires à celles de Brahmanes du 2ème millénaire avant notre ère.
Une hypothèse serait que la tradition chrétienne soit elle-même dépositaire, ou récipiendaire, de traditions beaucoup plus anciennes, dans lesquelles les principes de ces conceptions antiques auraient été conservées.
On sait que le symbolisme chrétien des portes solsticiales, associé aux fêtes des deux Saint Jean, (et folkloriquement associées au feu et à la lumière), est l'héritier du culte latin du dieu Janus.
Or dans une remarquable étude sur les anciennes divinités du feu, où la mythologie comparée est constamment soutenue par l'étymologie indo-européenne, Jean Haudry a relevé une impressionnante série de correspondances entre les formes les plus archaïques du dieu Janus (originellement dieu-feu), et l'Agni védique.
Ces deux dieux ont notamment en commun trois traits bien caractéristiques, qui les qualifie comme "dieux des commencements", "dieux des dieux", et "non-dieux", ce paradoxe s'expliquant par le fait que leur essence est, d'un certain point de vue, réellement identique au feu matériel.
Par d'autres caractères, cette famille de dieux se trouve apparentée à celle des divinités du foyer, comme la déesse grecque Hestia, qui, dans la tradition pythagoricienne, représente spécifiquement le feu ou le point central.
A partir de ces constatations, deux hypothèses semblent envisageables.
La première serait que, d'un fond archaïque indo-européen au culte latin de Janus, et de ce dernier aux conceptions chrétiennes du moyen âge, la transmission des principes ait eu lieu à chaque fois de façon "régulière", et suffisamment complète pour que la doctrine ait conservé, à travers ses formes successives, un caractère opératoire réellement universel, lui assurant de "produire toujours les mêmes résultats".
La seconde serait, encore plus simplement que, par le biais de la continuité de la tradition italique, bien mise en évidence par André Charpentier, "De Pythagore à Virgile et de Virgile à Dante, le fil de la tradition n'ait jamais été rompu", pour reprendre la formule de René Guénon.
VI. EPILOGUE : RECAPITULATION GEOMETRIQUE ET ALCHIMIQUE
Notre enquête nous a conduit jusqu'à un dieu-principe, dieu-feu, dont "l'existence" est bien balisée dans la mythologie indo-européenne.
On peut poser la question : ce feu divin, ce feu mythologique, peut-il être ressaisi sur un plan ésotérologique différent (et ordonné à la science de la nature) qui est celui de la doctrine des éléments ?
Nous proposons de ressaisir l'ensemble de la peinture dans une perspective alchimique dessinée par Guy-René Doumayrou, s'appuyant sur les cinq polyèdres réguliers et les correspondances élémentales suggérées par Platon.1. Le centaure et le capricorne
Derrière cette scène de chasse transparaît le « combat des deux natures », que notre hermétiste associe aux éléments de l'air et du feu, soit géométriquement l'octaèdre et le tétraèdre. (note 15)
Remarquons que ces deux figures apparaissent comme complémentaires dans la construction du gnomon du tétraèdre, qui permet de remplir l'espace.
2. Le rectangleL'icosaèdre, qui est donné dans le Timée comme la forme propre de l'élément eau, reflète adéquatement le thème du filet métallique que fabriqua Vulcain (note 16) :
« Dans l'optique de la genèse il ne peut s’agir que de l’eau amniotique. Cet adjectif dérive du grec "amnos" qui signifie "agneau" c’est à dire "jeune bélier", pour nous dire que cette eau apporte un feu (dont le bélier est l’emblème), feu singulier qui lave l’embryon d’or dans son bain substantiel, comme la toison où les anciens orpailleurs retenaient les paillettes métalliques, ou comme un tamis. De la même toison était fait l’agrenon, ce mystérieux filet de laine nouée (la laine figure par ses mèches ondoyantes la flamme du bélier) qui enveloppait l’omphalos de Delphes. L’agrenon, conducteur du feu, est un filet d’étoiles qui élève l’embryon plus haut que les tempêtes. »Le nombre 515
reflété par les faces de l'icosaèdre
Quant à la description de l'icosaèdre gnomonique d'Edimbourg par Fulcanelli, elle ne peut que rappeler les origines chthoniennes de cet artifice propre à condenser l'énergie solaire :
« Ainsi cet icosaèdre étrange représente pour nous une œuvre de double gnomonique. Le mot grec γνώμων, qui s’est intégralement transmis aux langues latine et française (gnomon), possède un autre sens que celui de l’aiguille chargée d’indiquer, par l’ombre projetée sur un plan, la marche du soleil.
La racine grecque d’où proviennent γνώμων et γνῶσις, a également formé γνώμη, correspondant à notre mot gnome, avec la signification d’esprit, d’intelligence (...) La tradition nous les dépeint comme étant fort laids et de très petite stature ; en revanche, leur naturel est doux, leur caractère bienfaisant, leur commerce extrêmement favorable ».
3. La Jérusalem
La tradition décrit la Cité céleste comme un cube, puisque « la longueur, la largeur et la hauteur en étaient égales ». Cette forme, que Platon associe à l'élément terre, symbolise pour nous la mort initiatique ou « lyse d'amour », qui fixe dans l’arche cubique toutes les potentialités du monde, réduites en un nouveau chaos.
4. Le chrisme
Le « feu nouveau », en forme de X, signant l'accomplissement du sacrifice au centre de la Jérusalem, authentifie une mise au diapason avec la force animatrice de l'Univers, cet « amour qui meut le soleil et les autres étoiles », que Platon illustrait par le dodécaèdre.

Ou encore, selon Guy-René Doumayrou, « l’élévation du cube, retournement de la quadrature du cercle, annonce l’assomption des forces de la nature au delà de leurs propres limites. Le dodécaèdre représente le dynamisme vital (cinq) activé au delà de sa puissance naturelle par l’ordre solaire (douze). C’est l’emblème de la Quintessence ».
Notons, enfin, que la relation de dualité géométrique entre l'icosaèdre et le dodécaèdre fait écho, dans le domaine élémental, à celle entre l'eau "ignée" et le feu "nouveau", comme le dodécaèdre conserve, en partie, la symétrie de l'icosaèdre et la signature du nombre 515. (note 17)
24.09.2018
NOTES DE BAS DE PAGE
note 1 : Les enfants grecs, précise Antoninus Liberalis, ont coutume de couper la tête du lucane, et de la porter ensuite autour du cou comme un pendentif lyriforme.
note 2 : Associé au symbolisme du nombre 55, valeur en latin de l'expression numérale LVX, même si elle s'écrit ordinairement LV, (l'ajout du X ne changeant rien), mais aussi indirectement au 515, si l'on considère l'expression : cinquante (L) dix (X) et cinq (V) comme une variante du dantesque : cinq cent dix et cinq.
note 3 : Les sabots arrière du centaure entérinent la division du rectangle selon un rapport de symétrie gauche/droite. Le point situé entre les sabots correspond à l'axe du vav et de la séparation Mars/Vénus.
note 4 : Ce nombre pourra, en première lecture, apparaître comme une expression « arrondie » de la hauteur de la muraille de Sion.
note 5 : Le rapport entre ces deux points de jonction, 55 et 144, se laisse reconduire au rapport 10 – 12, et même, ultimement, au rapport générique entre pentagone et hexagone.
note 6 : On peut aussi lire, en miroir, 14 14 comme une écriture décimale de √2, mesure des 12 diagonales des faces d'un cube d'arête 1 ; quant aux 4 diagonales intérieures, elles mesurent √3, hauteur de l'hexagone de côté 1 et du triangle équilatéral de côté 2 : on pourra ainsi interpréter ce nombre comme un symbole du chrisme ou de l'ignition accomplie (c'est le rapport numérique qui apparaît dans le tracé du 4 de chiffre, entre la grande ligne et les deux plus petites).
note 7 : Dans le champ sémitique, la racine trilitère QLB, qui donne le mot coeur (qalb) signifie aussi retourner. Aussi Dieu est appelé Celui qui retourne les cœurs.
note 8 : En français, la déesse a donné son nom à la fleur de lys (iris), mais aussi au verbe iriser et à ses dérivés (irisation, iridescent) qui signifie : scintiller de mille couleurs, comme la fleur de lys ou l'arc en ciel.
note 9 : La partition de l'arche indique que le "catalyseur" de la chimie palindromique possède lui-même cette structure.
note 10 : De plus, à la jonction des 2 registres (vecteurs horizontaux) on a le rapport
11 + 12 = 23
Tandis que sur les parties latérales, on a (vecteurs verticaux)
9 + 14 = 23
Il s'établit donc une relation d' "équilibre" ou de commune mesure entre le rapport "ascendant" de la Jérusalem Céleste vers un état de complétude (11-12), et le rapport qui qualifie ses proportions internes (9-14).
note 11 : La différence c'est que la croix de Saint André se divise en rangées 2-4-4-2 au lieu de 2-4-6-6-4-2.
note 12 : Le fait que ce soit un carré gnomonique de rang 4 est concordant avec l'idée que cette zone est "le domaine de la plénitude". Ce carré, c'est le "filet" que la vesica piscis fixe en phase losange, au point intermédiaire de la "transformation du triangle en carré", c'est à dire à "l'instant X" de la physique pythagoricienne. Et cette grille est aussi celle du carré magique de Dürer.
note 13 : Notons en outre qu'à la fin de son exposé, Zellini hasarde un rapprochement avec certains aspects de la religion apollinienne, révélés notamment par Plutarque.
note 14 : Le nombre 10800 (= 1 année) rappelle le 1080 du helek hébraïque (= 1 heure), de la même manière que les 144 coudées de la muraille de Jérusalem rappellent les 1440 minutes d'une journée.
note 15 : La sagittation est un "forçage", un coup douloureux qui contraint les éléments à s'abouter en un point quelconque, violence rendue nécessaire par le fait qu'à l'image du Même et de l'Autre, ces éléments sont "rebelles au mélange".
note 16 : Le thème du filet renvoie naturellement à l'élément eau, comme l'illustrent les deux paraboles ésotériques, étrangement ressemblantes, relatant les pêches miraculeuses de Pythagore et du Christ. Le nombre de 153 poissons mentionné dans l'Evangile de Jean permet en outre d'établir un lien précis entre ces récits et le polygone gnomonique, puisque c'est par le rapport 265/153 qu'Archimède approche la mesure de la hauteur de la Vesica Piscis, "mesure du Poisson", égale à √3, qui correspond à la grande diagonale du losange gnomonique évoqué dans la note 12.
Dans une vision sommaire en phase avec la focale hermétique de Doumayrou, on pourrait voir le « combat des éléments » (sagittation) comme un conflit cosmogonique nécessitant d'être « luthé » dans le filet gnomonique; - filet qui peut indiquer aussi bien des proportions que le fait de réduire ou ajointer deux principes dans un « rectangle » unique, qui serait par exemple le lit nuptial ou le « cocon ». Alors la phase suivante signifierait plus proprement la hiérogamie, la « lyse » de Mars et Vénus permettant l’échange des spermes ou des codons ADN, et la création du nouvel être, « sel alchimique » (grain cubique) ou « papillon » (psyché)... qui se libère dans la phase du chrisme (« quintessence »).
Le filet joue deux rôles : amener les principes sur un terrain d’entente, et les dissoudre.
note 17 : En effet, si l'on pose un dodécaèdre sur l'une de ses faces, on a :
- une face pentagonale en haut (5)
- une face pentagonale en bas (5)
- et, formant une médiation entre ces deux pôles, 10 faces qui ne sont "ni en haut ni en bas" (10)
BIBLIOGRAPHIE ET LIENS UTILES
Sur les templiers, Saint Bernard et la religion du lys :
Cantique des cantiques
Les fils de la vallée - site de recherche sur la tradition templière
Saint Bernard : sermon 47 sur le Cantique des cantiques
John Joseph Stoudt : Consider the lilies how they grow
Sur la religion apollinienne et le centaure :
Marcel Détienne : Apollon le couteau à la main
Philippe Monbrun : Les voix d'Apollon
Georges Dumézil : Apollon sonore
Homère : Hymnes homériques à Apollon et à Hermès
André Charpentier : Le serment d'Hippocrate
Valérie Gitton-Ripoll : Chiron, le cheval-médecin ou pourquoi Hippocrate s'appelle Hippocrate
Jean Bayet : Le symbolisme du cerf et du centaure à la Porte Rouge de Notre-Dame de Paris
Plutarque : Que signifie le mot EI gravé sur la porte du temple de Delphes?
Sur le symbolisme des portes solsticiales, Janus, Agni
René Guénon : Symboles de la science sacrée
Porphyre : L'antre des Nymphes
Homère : L'odyssée
Jean Haudry : Le feu dans la tradition indo-européenne
Paolo Zellini : Gnomon, una indagine sull' numero
Ananda Coomaraswamy : La porte du ciel
Sur les deux tétractys 10 et 36
Armand Delatte : La tétractys pythagoricienne
-
Par zalmoxis le 21 Août 2018 à 08:45
DISCUSSION SUR LE PENTAGRAMME ET LE NOMBRE D'OR
AVEC LYSANDRE

La discussion débute par une remarque sur cette construction due à Yvo Jacquier, qui illustre l'article Vesica Piscis
Le 15/02/2017 par Lysandre
Intéressante, la construction avec le pentagramme. Si on l'interprète en géométrie projective, cette figure possède une signification bien précise, puisqu'elle équivaut à démontrer que l'on peut construire la polarité associée aux cinq sommets d'un pentagone quelconque. Démonstration belle comme du Bach, que je viens justement d'achever cette nuit...
Le 15/02 par Dylan G.
Ah oui ? Bravo ! En tous cas, on sent que cette figure doit gagner beaucoup à être interprétée projectivement, car il y a là une densité vraiment suspecte de "droites concourantes" et de "points alignés".
Je remarque que l'on a 10 points, comme dans la configuration de Desargues, et comme dans la tétractys. Sur ces dix points, 4 sont incidents au vesica piscis "intérieur", 4 autres au vesica "extérieur", les 2 derniers, les points AA', donnant l'axe de symétrie du même vesica. Au centre, on a le triangle d'or de Penrose avec la première étape de sa division : 1 obtus (en jaune, dans le dessin de Jacquier), 2 aigüs (en rose). Dans votre figure, il suffit, pour avoir ces trois pavés, de joindre C' à B', et B à E.
Le 15/02 par Raymond B.
Ah oui c'est bien intéressant.
Vu comme ça le théorème de Desargues m'a évoqué l'ennéagramme, où le "point de fuite" des deux triangles jouerait le rôle de centre caché qui règle le déploiement des 6 points en araignée 1/7 = 0.142857 pendant que les 3 points alignés sont imagés par le triangle 3-6-9.
Compte tenu de cette remarque, et par analogie avec Desargues, j'aurais eu tendance à voir, dans votre figure, deux lignes de 3 points concourir au point A (point rouge) pendant que les 2 épingles fichées dans les paumes de l'étoile, "s'alignent" au point A' en tant que formant un obtus "3-6-9". Les deux lignes forment un lambda avec le point A pour aiguille.
Le 15/02 par Raymond B.
Un peu dans le même "esprit", je voyais ceci chez Ouspensky le fidèle de Gurdjieff.
L'élément intéressant étant bien sûr la représentation avec 2 lignes parallèles. Parce que "projectivement" ça fait le joint entre les polygones et le point, ce dernier étant à l'infini (ce qui serait une manière élégante de concilier la mystique du Point avec celle... de son retrait). La ligne double pouvant à la limite être envisagée comme une figure fermée ; d'autre part, elle évoque ainsi "les eaux" ou protomatière des cosmogonies.
Le 17/02 par Lysandre
Mes démonstrations sont fondamentalement simples, elles consistent à "voir" projectivement la figure, par exemple, et tout s'éclaire de soi, sans recourir à de lourds appareillages algébriques. C'est magique, dans le bon sens du terme.
La GP est en soi une discipline très facile, qui permet de fonder toute la géométrie à partir de rien (trois axiomes ! pour toutes les géométries, euclidienne, comme non-euclidiennes, et même la géométrie différentielle, finalement... enfin), et tout le monde en principe peut l'apprendre, c'est sa simplicité même qui est désarmante. Mais elle n'est plus enseignée nulle part ! les matheux même ne la comprennent plus, ou plus assez... vous n'avez pas idée.
Bien sûr, il peut résulter de là des adaptations importantes pour les problèmes de pavages, etc. un pavage du plan projectif, c'est quelque chose de possible, et on en déduira forcément plusieurs pavages possibles du plan affin/euclidien, selon où l'on place la droite de l'infini, etc.
Ce sont des perspectives magnifiques, mais on ne peut progresser là-dedans qu'à petits pas.
Le 17/02 par Lysandre
Comme vous me paraissez capable de comprendre ces choses, que j'étudie avec émerveillement, je ne vois pas pourquoi je ne vous ferais pas profiter d'un petit exercice auquel je me suis livré sur deux figures intimement liées : je vous poste donc, ci-dessous, les deux, à savoir le diagramme de Petersen, que je me suis amusé à colorer avant de nommer ses points par des lettres, et la configuration de Pappus, dont j'ai nommé les points et droites de façon qu'ils correspondent au diagramme : en rouge, les points, en bleu les droites, et une boule rouge reliée à une boule bleue signifie : ce point appartient à cette droite. On obtient ainsi la configuration désirée, comme vous vous en apercevrez si vous essayez par vous-même, et de la façon dont je l'ai dessinée, on voit bien à quoi elle correspond : si la configuration "marche" ("holds" comme ils disent en anglais), alors deux perspectivités de mêmes centre et axe commutent, et donc le corps (des coordonnées, qui sous-tend le plan), est commutatif.
C'est la clef de toute la géométrie plane commutative, la "bonne" géométrie, bien ordonnée, que nous connaissons... elle tient toute entier dans le diagramme de P, figure bien plus symétrique et élégante que la configuration elle-même... mais il faut aimer ce qui est simple, et pouvoir apprécier l'esthétique des maths.
J'affirme de plus, ce qui est original, que le point au centre a une signification : si on le colore en une troisième couleur, vert par exemple, il correspond au plan lui-même, et signifie alors que si trois droites non concourantes/trois points non alignés, appartiennent à un même plan, alors toute la configuration est plane.
Le 17/02 par Dylan G.
Grand merci, Lysandre. Nous apprécions beaucoup cette gnose. En plus de la beauté de ces figures, l'exercice qui consiste à passer du diagramme à la configuration, et inversement, est particulièrement plaisant pour l'esprit.
Je remarque simplement, au passage, que si on introduit un "chrisme" au centre du graphe associé au solide de Dürer, on retrouve votre graphe de Petersen-Pappus. Autrement dit : Dürer + chrisme = Petersen.
 +
+  =
= 
Le 18/02 par Raymond B.
Y'a quand même une question que je me pose, peut être pas sans rapport avec la remarque sur le point vert...
Lysandre parle de la "géométrie plane commutative" comme étant la "bonne géométrie" que nous connaissons. Cette adéquation tient probablement plus pour lui à la notion de commutativité. Cependant, je me demande si "bonne géométrie" n'implique pas également planéité. L'idée, rapidement, serait que la géométrie solide "concrétise" ou développe (disons "une fois pour toute") la pellicule des figures 2D ; tandis qu'inversement, les figures planes sont des "abstractions" ou projections des volumes (mathématiquement : la projection est "surjective" ?), avec un statut quelque peu idéal et matriciel. Si la GP avait bien ce statut d'incontournable, alors dans le cadre de "l'espace naturel" RxRxR on se placerait naturellement dans un plan projectif, n'est ce pas ?
De manière un peu plus claire : l'opération de projection d'un volume sur une surface (comme notre rétine) est "surjective" c'est à dire que plusieurs corps peuvent "s'abstraire" d'un même "patron" plan. On pourrait alors dire que la figure plane est surdéterminée, et que c'est une forme d'interprétation ("réduction du paquet d'ondes") qui donne corps au volume. Pour parler comme Lacan, préserver cette équivocité serait alors nécessaire pour que la géométrie reste un lieu de dialogue avec l'inconscient, qui ignore le langage univoque de la logique aristotélicienne. La géométrie solide, sans être inutile à titre d'illustration ou de choix interprétatif particulier, ne possèderait pas les mêmes vertus "initiatiques" ou universelles que la géométrie plane. Hypothèses, bien entendu.
Le 18/02 par Lysandre
En n'oubliant pas, tout de même, qu'on peut faire de la géométrie projective en 3D, en 4D ou plus... il y a de la GP en toutes sortes de dimensions. Simplement, on commence par l'étude du plan parce qu'elle est plus "simple", tout en recelant la possibilité de géométries plus bizarres, "non-arguésiennes", donc nécessairement planes, mais les "plans" en questions sont en fait des structures très "exotiques"...
Par ailleurs, quand on étudie la géométrie dans l'espace (GP en 3D), il est naturel de se référer constamment à l'étude du plan, comme dans le plan on se réfère à l'étude de la droite... ainsi, quand j'étudie une quadrique en 3D, je vais le faire par le biais de ses sections planes : je vais la "découper en tranches" planes, étudier ces tranches, puis la réassembler en quelque sorte... et c'est comme ça que j'aurai une vision d'ensemble de la forme.
On peut certes penser aussi aux "niveaux du langage" comme à des "plans de coupe"... l'opération de "couper par un plan" est fondamentale en GP de l'espace, et on peut sans doute y voir une analogie avec d'autres disciplines.
En maniant toutefois les termes et les analogies avec prudence...
Le 18/02 par Dylan G.
La linguistique guillaumienne (héritière de Gustave Guillaume) définit toutes les structures profondes du langage au moyen de coupes transversales successives, effectuées le long d'un processus spatio-temporel, une sorte de psychomécanisme, ou de "geste" linguistique fondamental, qui lui reste toujours le même.
Emoustillé par ces histoires de pentagramme, je viens de relire avec bonheur la belle étude que Charpentier a consacrée au Vesica piscis (l'oeuf du monde, à lire ici). Dans la partie mathématique (pages 19-26), il évoque en particulier les constructions de Dürer avec le pentagramme, avec des considérations très intéressantes, puisqu'il associe cette construction avec les idées de vibration, de pulsation, de flamboiement, d'une part ; et corrélativement, avec des considérations "rétiniennes" (l'oeil qui voit tout), idées qui me semblent résonner avec tes propos, Raymond.
En supposant une dualité entre "flamme" et "rétine", entre "production" et "réception" de la lumière.
...
Tes remarques sur la planéité m'ont fait penser à une autre chose encore, dont personne ne parle jamais, mais qui m'a toujours plongé dans une profonde perplexité.
Sur le plan cosmologique, les groupements significatifs ne sont pas des sphères, mais des disques : des plans. L'écliptique est un plan, la voie lactée est un plan. Et en suivant ce chemin, on constate qu'à chaque fois, l'opération qui consiste à reconduire un objet (lui donner ses coordonnées) dans le groupe "monadique" supérieur auquel il appartient revient à le ramener sur un plan. Le processus étant "itératif" dans le sens du macrocosme, que se passe-t-il si on suppose que la dernière opération (celle reconduisant les parties au tout) est identique à toutes celles qui l'ont précédé? Il se passe que l'univers aurait essentiellement la structure d'un plan, duquel déborderaient au mieux quelque cloques monadiques originelles, matrices de toutes les monades inférieures. Et en poussant le vice un peu plus loin, on peut se demander si la procédure "d'exhaustion" qui conduit à faire disparaître "l'illusion" de la profondeur dans le sens du macrocosme, ne produirait pas un résultat semblable en sens inverse, dans une enquête sur les microcosmes, contraignant ces cloques mêmes à se résorber sur leur "équateur", et l'univers entier à se révéler n'être qu'une crêpe intégrale, dans laquelle rien n'aurait jamais connu la troisième dimension...
Le 20/02 par Raymond B.
"Soufflante" ta remarque sur la crêpe cosmique.
Ces réflexions sur le plan m'ont fait penser à un autre problème, qui concerne lui l'organisation de la science.
Parallèlement à l'entreprise scientifique de réduction, justifiée jusqu'à un certain point, chaque échelle possède un "plan de consistance" propre, avec un vocabulaire opératoire taillé sur mesure. Ce qui rend la biologie en partie rebelle à la chimie, elle même en excès sur la physique, etc...
Voilà la préface d'un cours de thermodynamique, que je rends en résumé, et qui pose des mots sur ce "changement d'échelle" créateur, qui serait peut être analogue à un "interdit de l'inceste" épistémologique, un partage des eaux entre conscient et inconscient, ou entre niveaux de réalité à la Nicolescu.
" Les concepts de chaleur, énergie interne, entropie, sens privilégié d’évolution, apparaissent à chaque fois que pour un système mécanique, l’on fait une division entre deux niveaux d’échelle, et un partage de notre connaissance (et de notre ignorance) entre ces deux niveaux. Le passage d’une échelle à l’autre ne peut en général faire l’économie d’hypothèses de nature statistiques supplémentaires par rapport à l’axiomatique du niveau mécanique de départ.
Au niveau de ce que l’on appelle mécanique, on manipule des points matériels, des forces, de l’énergie, etc... On envisage ensuite des ensembles constitués d’un grand nombre de ces points et l’on souhaite traiter ces ensembles en utilisant les mêmes concepts qu’au premier niveau. On appelle thermodynamique cette théorie de deuxième niveau.
C’est dire que selon nous, la thermodynamique est avant tout la science du changement d’échelle, et non seulement la science des transformations de l’énergie. La mécanique rationnelle montre déjà des transformations d’énergie (...) Quand une réaction chimique dégage de la chaleur il s’agit du même phénomène, un peu plus caché, où une énergie potentielle électromagnétique est en partie transformée en énergie cinétique d’agitation des molécules du système (...) Cette distinction d’échelle permet d’établir toutes les notions originales à la thermodynamique par rapport à la mécanique et éclaire aussi les questions relatives au temps et à son irréversibilité, au hasard, etc..."Le 20/02 par Lysandre
Merveilleuse, votre trouvaille sur le solide de Dürer!
Vérification faite, le solide de Dürer et la configuration de Pappus ont effectivement le même graphe. Cela veut dire que le solide de Dürer lui-même peut être vu comme un graphe de Pappus en trois dimensions ; et pour retrouver les 3 lignes manquantes (chrisme), il suffit de joindre les milieux des arêtes opposées des deux faces triangulaires que comporte le solide.


Le graphe correspond au solide vu en projection. On distingue bien les deux faces triangulaires et les six faces pentagonales.
J'y vois tout de suite diverses interprétations possibles... S'il existe une configuration non planaire qui correspond au même graphe, évidemment, il doit y avoir un lien entre le solide et la configuration, du coup... je note qu'on a dans ce solide des pentagones inscrits à une même quadrique (qu'on l'appelle "sphère" ou autrement, peu importe), donc inscrits aussi aux coniques selon lesquelles leurs plans coupent la sphère... et vous savez qu'un pentagone détermine entièrement sa conique inscrite, donc il y a là quelque chose...
NB. Si, comme je le pense, il y a bien une signification au point central de Petersen - le plan - alors cela porte le nombre des sommets du graphe à 19... nombre qui n'est pas indifférent, eu égard à certaines considérations ésotériques...
Le 21/02 par Dylan G.
Je remarque que votre 19 semble induire une récurrence de forme : 1+6xn entre
A. Plan de Fano. 1+6x1
B. Plan à 13 points. 1+6x2
et donc
C. Pappus. 1+6x3
Comme si les principales configurations auto-duales de la GP s'enchâssaient l'une sur l'autre, sur fond de nombre hexagonal centré. « Desargues » faisant exception à cet égard.
Le 21/02 par Lysandre
Oui, bien sûr, j'avais déjà relié cela à la série des nombres hexagonaux centrés. Cela me paraît la base de tout, du point de vue des développements herméneutiques possibles en tout cas.
Le 22/02 par Dylan G.
J'ai comme l'impression que les deux sujets qui vous occupent en ce moment : le pentagone, et la configuration de Petersen-Pappus, sont intimement liés l'un à l'autre. Et ceci me ramène au polyèdre de Dürer, dans sa fameuse version "dorée" construite à partir d'un angle de 72°, sur lequel j'ai glané une petite documentation complémentaire, sur le site que Yvo Jacquier a consacré à ce solide (à visiter ici).
Admis que le polyèdre de Dürer pouvait être vu comme un graphe de Pappus en 3 D, je trouve intéressant que le pentagramme étoilé apparaissent dans cette formulation tridimensionnelle, et décliné harmoniquement sur 3 degrés. Les deux réalités, pentagramme et polyèdre de Dürer, sont intimement entrelacées dans leur structure... au point que ce caillou de Dürer vous a comme un petit air de pierre philosophale.
Le dossier d'images que j'ai réuni comprend. Figure 1 : Le solide - un rhomboèdre, qui est un cube étiré sur l'une de ses diagonales - dont il faut partir pour obtenir le polyèdre de Dürer par troncature de deux petits tétraèdres aux sommets. La face du rhomboèdre est un losange d'angles 72° et 108°, qui peut être regardé comme une variante du losange "vesica piscis", d'angles 60° et 120°; par où on saisit une certaine continuité dans les idées de Dürer. Figures 2, 3 et 4 : trois représentations de la structure du même rhomboèdre, dans lesquelles apparaissent 3 différents pentagrammes étoilés, dont les segments de référence ont respectivement pour valeur : Phi, 1, et 1/Phi : ces trois mesures déterminant un maillage continu. Je suppose que ces trois valeurs correspondent à trois échelles successives du triangle d'or de Penrose, mais il est intéressant que ce que l'on connaissait comme un problème de "pavage" se présente ici plutôt comme un problème de "maillage". Et je pense qu'il doit être plus intéressant encore d'envisager cela avec vos méthodes projectives, en terme de coniques, etc.



PS : Du coup, le "point vert" est le barycentre du solide de Dürer?
Le 22/02 par Lysandre
100% d'accord avec vous; je n'ai rien à ajouter... sinon qu'il est fort possible qu'une partie au moins du travail ait été fait, mais se trouve actuellement dans des ouvrages inaccessibles, anciens, épuisés, conservés dans de lointaines bibliothèques... parfois on gagne du temps à refaire les choses par soi-même, au lieu de chercher des ouvrages de référence à peu près introuvables, et il en existe tant... c'est une donnée avec laquelle j'ai appris à faire. Mais d'un autre côté, je m'aperçois que même dans les ouvrages de référence, les choses ne sont pas toujours aussi bien "faites" que quand je les fais ; de très bons auteurs présentent parfois des démonstrations boiteuses, selon les critères actuels ou ceux qu'on m'a appris... même chez mon maître, l'immense Buekenhout, j'ai réussi à trouver une démonstration qui ne me satisfait pas, et j'en ai imaginé une plus "projective" si l'on veut, encore que rien ne dit qu'il n'y avait pas pensé lui-même, mais il avait peut-être ses raisons qui m'échappent...
Le "nombre d'or" est un rapport. Mon intention est bien de le "traiter" un jour en termes de birapport, etc. Toujours reconduire le rapport au birapport, comme à ce qui l'engendre, voilà ma règle. C'est vers là que je me dirige, mais je me suis rendu compte qu'il y avait bien des étapes à franchir. Au moins, je commence à voir parfaitement ce que la classe des pentagones dits "réguliers" a de "spécial" au point de vue projectif (cinq rotations identiques, cela n'est pas donné a priori), c'est un bon début, je pense. Lentement mais sûrement...
NB rapport/birapport, la façon "simple" de voir le "rapport" c'est de se dire : deux points A, B sur une droite, un 3e point C quelconque peut toujours être vu comme le "milieu" de AB, selon la position d'un 4e point, conjugué harmonique de C par rapport à AB. Si ce 4e est le "point à l'infini", alors C est le "milieu" de AB. La notion de milieu, de médiane, etc. est donc ainsi ramenée à celle de conjugué harmonique, qui est fondamentale. On voit comment le nombre 4 est producteur d'harmonie.
Pour faire court, "conjugué harmonique" se traduit par "birapport = -1"
Le 24/02 par Dylan G.
Au sujet de la configuration de Desargues, je me suis fait une remarque un peu du même genre que celle qui consiste à "voir" dans le solide de Dürer un graphe de Pappus. Dans les deux cas, il s'agit d'interpréter une configuration planaire de la GP en fonction d'une formulation tridimensionnelle particulière.
On part de cette magnifique représentation du théorème de Desargues construite sur un tétraèdre, due semble-t-il à Burkard Polster, dans laquelle 4 points correspondent aux sommets du tétraèdre, et les 6 autres aux arêtes du même tétraèdre, tenues "par les milieux". On constate que ces 6 points correspondent aux sommets d'un octaèdre inscrit dans le tétraèdre.
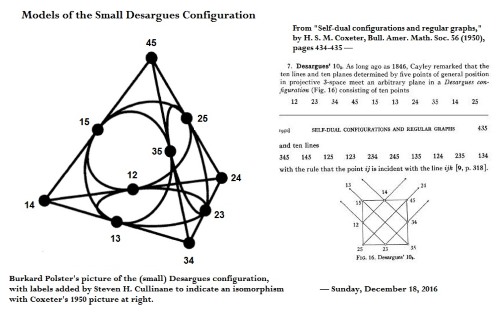

Toutes ces relations se retrouvent dans un tétraèdre gnomonique de rang 2, composé d'un octaèdre (ci-dessus en blanc, au centre) et de 4 tétraèdres (ici trois gris et un rouge). L'octaèdre possède bien sûr 8 faces triangulaires, dont 4 sont cachées dans la structure du solide, et 4 visibles à la surface, qui correspondent aux quatre cercles de la configuration de Desargues.
Sous ce regard, on peut m'accorder que le tétraèdre gnomonique de rang 2 est une configuration de Desargues en 3D?
Je trouve que cette représentation tétraédrique de la configuration de Desargues est aussi la plus pertinente pour coordonner Desargues avec la tétractys. En effet les 4 "points-sommets" du tétraèdre peuvent être assimilés au "trépied" de la tétractys; tandis que les 6 autres points, les points-arêtes, ont un rôle de médiation qui permet, au moins symboliquement, de les associer aux six points de l'hexagone.Le 25/02 par Lysandre
C'est "à peu près" ça, sauf que dans la configuration de Desargues en 3D, si 45 est le centre de la perspective, les points 15, 35, 26 respectivement les images des points 14, 34, 24, alors les trois derniers points sont, par exemple, le point x, intersection des droites 15.35 et 14.34.
Le point 13, donné sur l'image, est le conjugué harmonique de x par rapport à 14 et 34. La donnée de l'un permet de retrouver l'autre. C'est comme si on avait combiné une perspective de Desargues avec une réflexion dans le plan 14, 34, 24, pour remettre tous les points "à l'intérieur" du tétragramme.
Sinon, l'octaèdre existerait de toute façon, mais il aurait une forme moins "régulière"...
Cette figure contient donc toute l'"information" nécessaire pour retrouver la configuration de Desargues, mais ce n'est pas exactement ce qu'elle est ; (à moins encore qu'on ne considère les cercles 15, 35, 13 etc. comme des "droites", alors bien sûr...). On a voulu y mettre autre chose en plus, cf. Petersen - Pappus.
Il faudrait que je trouve le temps d'analyser davantage cette figure.
Le 25/02 par Dylan G.
Vous écrivez : "... à moins qu'on ne considère les cercles 15, 35, 13 etc. comme des "droites", alors bien sûr..."
Pour moi, c'était une évidence, sans quoi ce que je vous écrivais n'a pas de sens. La configuration doit impérativement compter 10 points et 10 droites, sans quoi le tétraèdre n'aurait pas de pertinence.
Le but de ma remarque n'était pas de faire de la géométrie, mais d'établir une correspondance idéelle, entre Desargues et les points de la tétractys, - ce que permet à mon sens cette formulation tétraédrique (via le tétraèdre gnomonique de rang 2).
Mais je pense que mes explications manquaient de clarté et ça ira sans doute plus facilement avec 3 petits dessins.
Figure 2. Dans la tétractys, je nomme "points majeurs" les points ABCD reliés par un trépied, correspondant aux arètes d'un grand tétraèdre vu de haut, et "points mineurs" les points u, v, w, x, y, z qui parcourent l'hexagone "tournant" sur le même centre que le trépied. Et je constate que rien n'interdit de considérer cet hexagone comme un octaèdre, doté de 4 faces sombres (les droites-cercles de la configuration de Desargues = faces visibles de l'octaèdre, dans notre tétraèdre gnomonique), et de 4 faces claires (les faces cachées de l'octaèdre), que l'on visualise mieux en les nommant. Faces sombres : (uvz), (vwx), (xyz), (uwy). Faces claires : (uvw), (wxy), (yzu), (vxz). Une fois notre octaèdre défini, on supprime le trépied reliant les points ABCD et on considère ces points comme flottant sur une sphère circonscrite à l'octaèdre. On comprend que ces 4 points doivent être les sommets de 4 petits tétraèdres dont les bases sont les faces "blanches", les faces "négatives" de l'octaèdre. Pour le point A la solution est évidente. Figure 3 : le point A est le sommet d'un petit tétraèdre dont la base est le triangle clair (zvx). Mais on saisit que la solution est essentiellement la même pour les trois autres points. En l'occurrence : le point B est le sommet d'un "tétraèdre" dont la base est le triangle clair (uvw), le point C, le sommet d'un tétraèdre dont la base est le triangle clair (wxy) et le point D, le sommet d'un tétraèdre dont la base est le triangle clair (yzu).
Bien sûr, cette tétractys n'est pas "représentable" en 2 dimensions (ou alors de manière paradoxale) cependant j'estime qu'elle "existe" sur un plan purement idéel. On peut donc coordonner de la sorte les points de la tétractys avec ceux de la configuration de Desargues (Figure 4). Si l'on ajuste le point A au point 45, les 3 autres points majeurs BCD s'ajustent, par exemple, aux points 24, 34 et 14, et les 6 points mineurs, sommets de l'ocatèdre, s'ajustent en conséquence selon la règle : une face sombre de l'octaèdre correspond à une droite-cercle de la configuration de Desargues.
Le 25/02 par Lysandre
merci pour ces passionnantes réflexions.
J'avais en effet compris que "votre" interprétation du tétraèdre-Desargues supposait de considérer les cercles sur chaque face comme des "droites", mais je remarque juste que cela revient à considérer chaque face comme un plan de Fano ; lequel n'est pas généralisable en trois dimensions, mais comme diagramme 3D de la configuration de Desargues, cela fonctionne tout de même, avec en plus le fait qu'on peut considérer les points 15, 12, 23 comme conjugués harmoniques des points de fuite, de sorte que le théorème s'énonce simplement en disant que les conjugués harmoniques de ces points sont alignés.
C'est une représentation intéressante, à laquelle je n'aurais certes pas pensé, mais qui vaut d'y réfléchir. Je vous l'accorde volontiers.
Oui, on pourrait même se demander si, ayant quatre coniques tangentes deux à deux, comme cela, sur les faces d'un tétraèdre, le fait d'exiger l'alignement des conjugués harmoniques équivaut à Desargues... il y a un rapport entre Desargues et les coniques/polarités à la base : supposer un plan arguésien équivaut à peu près à supposer l'existence de polarités/coniques, ce n'est pas trivial à voir mais c'est clair. On peut donc creuser la réflexion longtemps avec cette figure. Je vais sans doute un jour ou l'autre l'inclure dans mon travail, mais si je disposais des articles de Polster et de Coxeter - auxquels se réfère la planche avec les sommets du tétraèdre numérotés - cela m'aiderait.
Sinon, j'avance avec les pentagones, plus vite que je ne craignais. Ayant extrait les conditions de symétrie - et il est assez beau de voir que tout pentagone ayant deux axes/centres de réflexion en a forcément 5 et est donc "régulier" par rapport à "sa" conique - je m'essaie maintenant à donner des coordonnées à tous les points/droites de la figure, A, B, C, D, E, A', B', C'... etc. Après, ce sera un jeu d'enfant de calculer tous les birapports possibles et imaginables.
J'ai remarqué, au passage, que, dire qu'un point (X, Y) d'une droite a pour coordonnée X/Y (coordonnée affine) le nombre d'or, équivaut à dire que l'involution (X, Y) --> (X + Y, X - Y) (cette application définit bien une involution de la droite, facile à vérifier) laisse invariante, pour ce point, la "forme quadratique" XY. En effet, cette assertion équivaut à l'équation (X + Y)(X - Y) = XY, ou X^2 - Y^2 - XY = 0, où l'on reconnaît facilement l'équation du nombre d'or.
Je devrais donc, à un moment, pouvoir exprimer cela en termes d'une involution qui commute avec une forme quadratique, pour un certain ensemble de points.
NB. Mes parents ont l'habitude de mettre des pommes en vrac dans un seau d'eau, pour les laver. Elles se mettent alors à flotter, et adoptent spontanément une disposition très parlante : une au centre, et six autres autour, tangentes deux à deux... le diamètre du seau équivalant juste à trois pommes à peu près. Je m'émerveille à chaque fois de constater à quel point la division hexagonale du "cycle" est naturelle, et le fait qu'on la retrouve partout... Dans mes développements sur la question, le passage où j'explique Petersen et Pappus, les dix-neuf points (et le rapport avec la racine de 361 etc.), je cite cette "expérience", pour bien faire comprendre au lecteur l'absence (ou quasi ?) d'arbitraire dans tout cela... En tout cas, ça me réjouit toujours de voir ces pommes flotter comme ça, alors que personne ne l'a fait exprès : elles "connaissent" spontanément l'empilement maximal de leur plan !
Sur ce, je retourne à mes pentagones.
Le 25/02 par Lysandre
Chers amis, eh bien! victoire, je crois que c'est le mot...
Sur la figure que je vous poste, vous pouvez voir comment le nombre d'or "apparaît" naturellement sur un pentagone ayant deux axes/centres de réflexion :

commençons par construire le quadrilatère complet O, I, I', I'' ; pour que le pentagone ait au moins un axe de réflexion (KM, avec pour centre J), nous prendrons le 5e point A sur KM. AI' coupera alors OI en D. Pour que le pentagone ait un 2e axe de réflexion, disons I''D (avec pour centre N), il faut que l'on ait (N L A O) = - 1.
Dans le repère (O, J, K, I), il en résulte (après quelques calculs très simples que je vous passe) que A aura pour coordonnées (X, Y, 1) avec X/Y = (3 - √5)/2. On en déduit alors, par quelques calculs supplémentaires, que le birapport (N B C A) vaut (1 + √5)/2 en valeur absolue, et si l'on suppose que la droite de l'infini passe par N, alors ce birapport se réduit au rapport AB/BC.
Vous voyez, c'est aussi simple que ça... deux axes de symétrie, et on a le nombre d'or, comme birapport de quatre points bien choisis.
Pas besoin de considérations métriques ni rien... nous avons officiellement "réintégré" le dit nombre d'or dans la GP. Ces petites choses illuminent ma journée.
NB. Une précision quand même (rappel au cas où) : le birapport de quatre points P1, P2, P3, P4, bien sûr, se calcule sur la base de leurs coordonnées homogènes selon la formule :
(P1 P2 P3 P4) = (X3Y1 - X1Y3)(X4Y2 - X2Y4)/(X3Y2 - X2Y3)(X4Y1 - X1Y4)
on peut aussi utiliser les coordonnées X, Z ou Y, Z à la place de X, Y, du moment qu'aucun des facteurs ne s'annule, car un birapport n'est pas censé valoir 0 ou l'infini (si les quatre points sont distincts). C'est plus élégant écrit à l'aide de déterminants, mais ça va plus vite comme ça... important quand même, car il ne faudrait surtout pas essayer, dans ce contexte, de calculer le birapport comme un rapport de rapports de "longueurs de segments" ou distances entre points, comme dans le plan euclidien... c'est évident quand on a l'habitude, mais il faut penser aux autres aussi...Le 26/02 par Dylan G.
Bravo Lysandre, pour ce résultat, comme pour sa présentation très pédagogique! Même si vous le jugez simple, il me paraît d'utilité publique, particulièrement dans les affaires pythagoriciennes.
La boucle est bouclée, d'une certaine façon. Je trouve que cela mérite une petite coupe de champagne.
Le 26/02 par Raymond B.
Merci, ça fait du bien en effet !
Le 26/02 par Lysandre
Eh bien, à votre santé ! J'espère que c'est un bon millésime :).
DECOUVRIR LA GEOMETRIE PROJECTIVE AVEC LYSANDRE :
OU LES PASSIONNANTES AVENTURES
POUR APPROFONDIR LE THEME DE LA DISCUSSION :
PENTAGONE ET GEOMETRIE PROJECTIVE
Ressources documentaires et crédits images :
Yvo Jacquier : Etude géométrique du polyèdre de Dürer dans sa gravure Melencolia, chap. 2
André Charpentier : L'oeuf du monde, pp 19-26
Harold Scott MacDonald Coxeter : Self-dual configurations and regular graphs, Bulletin of the American Mathematical Society, n°56. 1950, pp 434-435
Burkard Polster : A Geometrical Picture Book, Springer, 1998.
 Suivre le flux RSS des articles de cette rubrique
Suivre le flux RSS des articles de cette rubrique