PAVAGES CELLULAIRES

 

 

par Guillaume DENOM

 

 

"On remarque que la série des hexagones cellulaires est identique à celle des gnomons du cube." 

 

 

 

ARGUMENT : Le nombre figuré et le nombre polygonal sont deux procédés traditionnels visant à représenter des nombres par des figures. S'ils bénéficient d'une certaine popularité dans le grand public, ils sont peu considérés des mathématiciens, en raison d'un préjugé - justifié - d'inintérêt, ou d'inintelligence mathématique.

Les défauts de ces théories peuvent se résumer en deux points :

1. Le déploiement de la série des polygones dans un même plan est impuissant à rendre compte des problèmes de symétrie très singuliers auxquels renvoie individuellement chacune de ces figures. Ainsi le carré, le pentagone et l'hexagone, renvoient à trois problèmes de symétrie très différents, et non homologues, et qui nécessiteraient, pour être exprimés de façon pertinente par des nombres, de déployer d'autres dimensions que celle du plan.

2. Les deux théories souffrent d'un défaut rédhibitoire, qui est le statut paradoxal du point, lequel devrait, selon leurs attendus, être à la fois un triangle, un carré, un hexagone, et bien d'autres choses encore.

Ce raccourci non exhaustif (bien que logiquement suffisant) du problème, nous est imposé par le fait qu'il existe, en réalité, plusieurs théories du nombre figuré, comme du nombre polygonal, cette dispersion même étant l'indice du fait qu'il n'existe, en vérité, aucune théorie mathématique digne de ce nom, derrière ces représentations diverses.

Malgré ces défauts, le succès de ces représentations semble traduire un sentiment latent, qu'il y a, peut-être, quelque chose d'intelligent à vouloir associer nombres et figures. La théorie des pavages cellulaires permet de rouvrir ce débat d'un point de vue a priori modeste et convivial, qui est celui de la logique élémentaire, et de lui apporter une réponse positive.

 

 

 

 

 

La théorie des pavages cellulaires constitue un ensemble de lois mathématiques qui, habituellement, sont abordées par deux approches mathématiques différentes : les problèmes d'empilement compact de cellules discoïdales ou sphériques, d'une part, et les problèmes de tessellation - ou de pavage - du plan ou de l'espace, par des polygones ou des polyèdres, d'autre part.

Nous allons voir que cette séparation des approches n'est pas nécessairement justifiée, dans la mesure où la théorie des pavages cellulaires se situe précisément à l'interface entre ces deux domaines.

Pour commencer, les idées physiques associées à la notion d'empilement compact pourraient même, ici, susciter une certaine confusion. En effet, au sens physique, les carrés et les cubes cellulaires sont considérés comme des structures « non compactes ». On veut dire par là qu'on ne peut les engendrer en laissant agir une force telle que la pesanteur. Les cellules ne se rangent pas « toutes seules ». Mais un peu de réflexion nous convainc que les pavages qualifiés de compacts, tels que les pavages hexagonaux, ne le sont, dans l'absolu, qu'en raison des forces physiques qui s'exercent sur eux de l'extérieur, dans l'environnement qui est le nôtre. A l'échelle microscopique, où l'action de la pesanteur devient négligeable, la nature ne montre aucune répugnance pour les arrangements cubiques, puisque ceux-ci abondent dans les systèmes cristallins ; et il est assez simple de créer un système de forces où, même à l'échelle macroscopique, les empilements cubiques s'avèrent aussi « stables » ou « compacts » qu'on peut le souhaiter, au moyen de billes magnétisées par exemple. Dans notre approche, qui est avant tout topologique, tous les systèmes doivent donc être envisagés comme virtuellement « compacts », au sens de « solidaires ».

Quoiqu'il en soit de ces questions, nous allons voir qu'en mathématique pythagoricienne, le traitement des pavages cellulaires dans une théorie unitaire et indépendante est justifié par deux raisons suffisantes.

1. Ils se prêtent à une classification quadridimensionnelle analogue à celle des objets gnomoniques, comme à celle des objets fondamentaux de la géométrie pythagoricienne.
2. Comme la théorie du gnomon, ils se rapportent au problème logique de la reconstitution d'objets, (fondamental en mathématique pythagoricienne, et qui relève, en soi et pour soi, de contraintes logiques plus sévères qu'on ne le suppose habituellement), dont ils prolongent et complètent la théorie.

 

Dans le tableau ci-dessous, les cellules 2D (cercles ou disques) sont représentées en noir, et les cellules 3D (sphères ou boules), en d'autres couleurs.

 

 

CLASSIFICATION QUADRIDIMENSIONNELLE DES ELEMENTS

 

	Dimensions    euclidiennes         D2	D3
Dimensions  pythagoriciennes  P1. POINTS    (1, 1, 1, 1, ...)
P2. SEGMENTS    (2, 3, 4, 5, …)
P3. PLANS  (Polygones  cellulaires)  Triangles    (3, 6, 10, 15, ...)      Carrés    (4, 9, 16, 25, ...)        Hexagones    (7, 19, 37, 61, ...)
P4. SOLIDES  (Polyèdres cellulaires)	X	Tétraèdres                         Cubes  (4, 10, 20, 35, ...)           (8, 27, 64, 125, ...)        tétraèdre de rang 6             cube de rang 5        83 cellules                        216 cellules         Octaèdres                       Cuboctaèdres  (6, 19, 44, 85, …)         (13, 55, 147, 309, ...)             octaèdre de rang 6      cuboctaèdre de rang 10        231 cellules                    3871 cellules

 

 

Pour chaque catégorie d'objets, la formule entre parenthèses donne en gras la valeur du plus petit élément insécable de sa classe, et à sa suite la série des valeurs pour lesquelles l'objet est reconstitué, par l'adjonction de cellules à cette structure de base. On remarque que l'objet « Point » ne peut, par nature, être « reconstitué » que par l'ajout répété de « zéro cellule », qui le laisse inchangé ; tandis qu'à l'opposé, l'objet « Segment » est reconstitué pour toute valeur entière supérieure à 2.

Dans l'absolu, il n'y a pas de nécessité à ce que les cellules soient jointives, la contrainte de « compacité » pouvant, à loisir, être remplacée par toute autre contrainte de répartition qui conserve les propriétés des structures. Mais pour cette étude introductive il a paru avantageux de considérer le cas le plus simple : celui de cellules de même dimension, empilées de façon compacte, sans discontinuité.

De la même manière, pour la classe des polygones, il a paru pertinent de se limiter dans un premier temps aux trois polygones qui, en version « classique » (non cellulaire) pavent le plan, savoir : le triangle équilatéral, le carré et l'hexagone.

Ces deux restrictions conduisent à exclure de la présente nomenclature des polyèdres tels que l'icosaèdre cellulaire qui, en raison de sa structure pentagonale, n'est constructible qu'en tant que surface, mais nécessite de ménager, à l'intérieur de l'objet, une région vide, où la périodicité des empilements est interrompue, - le pentagone n'étant pas une solution de pavage continu du plan.

 

 icosaèdre cellulaire

 

La famille des polyèdres pourrait néanmoins, sans déroger aux règles définies ici, s'enrichir de diverses de curiosités géométriques résultant, comme les structures ci-dessous, de la troncature de solides pythagoriciens classiques ; mais là encore on a jugé bon, dans un tableau élémentaire, de s'en tenir à l'appareil le plus réduit possible.

 

 exemples de polyèdres compacts engendrés par divers automates cellulaires, construits sur un réseau dodécaédrique rhombique

 

Quant aux structures non continuellement périodiques, comme celle de l'icosaèdre cellulaire, elles pourraient, elles aussi, être intégrées dans une classification plus large, définie dans le prolongement de celle-ci ; en tenant compte du fait que, du point de vue essentiellement génétique, ou généalogique, qui est celui de la logique pythagoricienne, elles relèvent d'un type moins simple, ou moins primitif, que celles du tableau ci-dessus. La remarque valant, également, pour les structures construites avec des sphères de dimensions différentes... - ou en modifiant encore d'autres paramètres.

 

On remarque que, dans cette logique, les dimensions « euclidiennes » D2 et D3 se présentent comme des « cas particuliers » des dimensions pythagoriciennes P1 à P4, qui relèvent d'un statut logique « plus général ».

 

Cette analyse quadridimensionnelle n'aura rien de déroutant pour les familiers de la mathématique pythagoricienne. On a vu dans une précédente étude que le Lambda de Platon était associé à une analyse quadridimensionnelle des propriétés du cube, dans laquelle les jambes gauche et droite du Lambda correspondent, respectivement, à la composition des cubes gnomoniques de rangs 2 et 3. Dans le cube gnomonique, c'est le petit cube atomique de valeur 1 qui joue le rôle de point.

Enfin, la même analyse quadrimensionnelle est associée, dans la tradition pythagoricienne, à la classification des objets fondamentaux de la géométrie en deux séries quaternaires : les objets premiers d'une part, les objets monadiques d'autre part.

 

 

 

LE PROBLEME LOGIQUE DE LA RECONSTITUTION D'OBJET

 

Il importe de bien distinguer la présente approche d'autres nomenclatures bien connues, auxquelles le lecteur a pu être confronté, comme celle des nombres polygonaux, ou celle des nombres figurés.

Ainsi, en apparence, la série des « triangles cellulaires » pourra faire penser à celle des « nombres triangulaires ». A une différence près toutefois, qui est capitale. Dans la présente approche, il n'y a rigoureusement aucune signification à énoncer que « les premiers nombres triangulaires sont : 1, 3, 6, 10... ». En effet, quand on ajoute le segment (oo) au point (o), on ne reconstitue en rien un objet. La valeur du premier triangle cellulaire est donc évidemment 3, et comme tel il constitue un élément insécable (en deçà de quoi il n'existe tout simplement pas de triangle), et ses compléments correspondent à la série des nombres entiers supérieurs à 2.

La présente classification étant entièrement gouvernée par le paradigme logique de la reconstitution d'objets, il est évidemment essentiel que les éléments premiers et insécables à reconstituer soient définis de la façon la plus rigoureuse. Au risque de paraître un peu trivial, on émettra cette pure évidence logique : pour qu'un objet puisse être reconstitué, il faut d'abord qu'il ait été constitué; les mots "constitué" et "reconstitué" correspondant sans coup férir, pour chaque objet de notre tableau, aux deux premières valeurs stipulées dans leur formule entre parenthèses, - ce couple suffisant par là-même à les définir.

En mathématique pythagoricienne, un objet se caractérise précisément par sa capacité distinctive à être reconstitué (inclus le cas limite où cette opération le laisse inchangé); capacité qui le manifeste en tant qu'individu, et le libère, ou si l'on peut dire, le détache, "une fois pour toutes les autres fois", de la chaîne des autres objets auxquels il est génétiquement apparenté. Dans cette conception, un objet ne peut être correctement défini sans qu'aient été produits avec lui, sur un même rameau, d'autres objets, membres d'une même famille; et l'on peut raisonnablement penser qu'il n'existe pas d'autre manière de procéder.

*

S'il restait des lecteurs convaincus qu'il est mathématiquement intelligent de procéder à la manière du nombre figuré, en commençant toutes les séries d'objets par le nombre 1, nous leur répondrons que ce n'est pas intelligent, mais que c'est, au mieux, tautologique, et au pire, faux, selon l'interprétation qui peut être donnée de cette représentation. En effet, si l'on commence toutes les séries par le nombre 1, on est aussitôt contraint de constater que les nombres importants, dans chaque série, sont le deuxième et le troisième. Commencer toutes les séries par le nombre 1 équivaut donc à proférer une tautologie du genre : "S'il existe des séries telles que : (2, 3, 4, ...), (3, 6, 10, ...), c'est parce qu'il existe aussi un nombre appelé 1 qui ne comporte qu'une seule petite boule." En raisonnant ainsi, on commet une grave erreur logique, qui est de confondre la constitution des objets avec celle du système.

Enfin, lorsque, selon une autre interprétation, ce n'est pas tautologique, c'est tout simplement faux.  Car il est faux de dire qu'une petite boule est à la fois un triangle, un carré, un cuboctaèdre, et une chaise. Ce paradoxe du point qui est tout et rien, propre à la théorie du nombre figuré, avait, du reste, interpellé nombre d'observateurs; - et l'on peut estimer qu'il est impossible de le résoudre correctement, sans recourir à l'analyse quadridimensionnelle.

*

On remarque que les polygones élémentaires se reconstituent au moyen de structures bien distinctes. Le triangle cellulaire se reconstitue au moyen de segments, le carré se reconstitue au moyen d'équerres, et l'hexagone se reconstitue au moyen d'anneaux hexagonaux. Il est naturel que la complexité du complément croisse en même temps que celle de la figure à reconstituer.

Il découle des remarques qui précèdent que, de la même manière que le côté d'un polygone cellulaire ne peut pas être inférieur à 2, l'arête d'un polyèdre cellulaire ne peut pas être inférieure à 2. Suivant ce principe, il s'avère aisé de déterminer le rang d'un polyèdre cellulaire quelconque, en comptant le nombre de cellules situées sur son arête. Par exemple, le cuboctaèdre d'arête 11 figurant dans notre tableau est le cuboctaèdre de rang 10, le tétraèdre d'arête 7 est le tétraèdre de rang 6, etc.

 

 

QUELQUES REMARQUES

 

 

Pavages polygonaux : principe général

 

Tout polygone cellulaire, triangle, carré ou hexagone, de quelque rang que ce soit, peut être pris comme élément de base pour former un pavage d'échelle spécifique. Toutefois, seuls les pavages carrés sont gnomoniques au sens restrictif qui nous est habituel ; c'est à dire qu'ils reconstituent la structure de l'élément de base par des solutions entières ; les pavages triangulaires et hexagonaux (construits, précisons-le, sur le même réseau cellulaire) nécessitant l'apport de compléments cellulaires, ces compléments étant eux même régis par des règles arithmétiques constantes.

 

Les pavages cellulaires hexagonaux présentent des propriétés arithmétiques intéressantes, en particulier à certaines échelles.

 

Pavages hexagonaux

 

La série des hexagones cellulaires correspond, dans la nomenclature des « nombres figurés », à la série des nombres hexagonaux centrés (1, 7, 19, 37, ...) ; à la réserve que nous avons déjà émise pour le triangle cellulaire, savoir : que la valeur atomique du premier hexagone cellulaire est évidemment 7, et non 1. 

 

 nombre hexagonal centré

 

 

On remarque que la série des hexagones cellulaires est identique à celle des gnomons du cube.

Pour former, à partir de n'importe quel hexagone cellulaire, un pavage d'échelle spécifique, on procède de la même manière qu'avec de simples cellules : on commence par disposer 6 pavés hexagonaux autour d'un pavé central, puis 12 autour de ceux là, puis 18, et ainsi de suite, comme dans l'illustration ci-dessous ; cependant on remarque qu'à chaque étape, les côtés de l'hexagone ne sont pas nettement délimités, mais se présentent comme des lignes brisées ; il manque à l'hexagone un certain nombre de cellules pour être complet, qui doivent donc lui être ajoutées.

  

Si on appelle E l'échelle du pavé de départ (correspondant à un nombre hexagonal centré donné), le complément latéral requis pour compléter le grand hexagone, de premier ordre, est de taille :  6 x E x (E-1)

Par conséquent la taille totale sera : 

 

Echelles

(1)               7 x 1 + 6 x 0 = 7

(2)               7 x 7 + 6 x 2 = 61

(3)               7 x 19 + 6 x 6 = 169

(4)               7 x 37 + 6 x 12 = 331

(5)               7 x 61 + 6 x 20 = 547

(6)               7 x 91 + 6 x 30 = 817

(7)               7 x 127 + 6 x 42 = 1141

 

Exemple ci-dessous avec un pavage formé de 7 pavés élémentaires de 61 cellules (échelle 5), que nous empruntons aux travaux de Jaime Vladimir Torres-Heredia Julca  : le complément latéral est de 6 x 20 = 120, et le grand hexagone compte donc 547 cellules.

 

 pavage de Torres-Heredia Julca

 

 

Cette structure peut également s'analyser comme la somme de 54 tétractys + les 7 points blancs au centre des hexagones 61.

Torres-Heredia Julca a montré qu'en faisant abstraction de l'hexagone central, aussi bien que des compléments latéraux, la structure de ce pavage pouvait être décomposée de la manière ci-dessous, en 6 x 60 + 6 (les 6 cellules blanches au centre des hexagones), et qu'à ce titre il fournissait une bonne approximation du cycle de l'année (6 x 61=366), dans laquelle les hexagones correspondent à des "bimestres". (On peut noter que notre actuel calendrier respecte, grosso modo, l'alternance entre mois de 30 et 31 jours, qui donne des bimestres de 61 jours). 

 

 

 

Suivant une indication de Dom Néroman, Rémy Bayoud a suggéré que cette structure pouvait apporter un éclairage sur l'une des plus anciennes cosmologies pythagoriciennes connues, due à Pétron d'Himère, selon laquelle il existerait "183 mondes, disposés sur un triangle". En effet le nombre 183 s'obtient en repliant cette structure sur un axe de symétrie médian, et correspond alors à un "semestre" de l'année. Une méthode encore plus satisfaisante consiste à interpréter la structure comme un "sceau de Salomon", et à rabattre un triangle sur l'autre en le faisant pivoter de 180° sur le centre géométrique de la figure, puisqu'alors on se retrouve même avec "183 mondes" disposés sur un triangle équilatéral.

 

Mais le pavage d'échelle 5 est encore remarquable à un autre titre, c'est qu'il engendre, en progressant dans les ordres supérieurs, une série infinie de nombres premiers, correspondant aux phases de reconstitution du grand hexagone. En effet, comme les nombres 61 et 547, les valeurs suivantes du grand hexagone sont toutes des nombres premiers et s'enchaînent avec la régularité parfaite qui peut être attendue dans un problème de pavage.

 

 

 

Cuboctaèdre cellulaire et dodécaèdre rhombique

 

 

Le caractère remarquable du cuboctaèdre cellulaire, c'est qu'il peut être envisagé comme « le gnomon de la sphère »... autant dire de la monade.

L'empilement cuboctaédrique de 12 sphères autour d'une sphère centrale peut légitimement être comparé, sur le plan logique, à l'empilement, dans un cube gnomonique de rang 3, de 26 petits cubes autour d'un cube central.

Les deux structures correspondent à une situation de « remplissage optimal de l'espace » autour d'une structure de base.

Précisons que, pour la sphère, cette conjecture sur le « remplissage optimal », considérée depuis longtemps comme certaine, n'a en fait été complètement démontrée que très récemment, en 2014.

Projeté sur un plan "équatorial", le cuboctaèdre correspond à la figure d'un sceau de Salomon inscrit dans un hexagone, structure particulièrement élégante, analogue à celle que l'on peut distinguer dans l'illustration ci-dessous.

 

 

Les 12 sommets des figures peuvent être mis en correspondance avec le dodécagone de nos horloges, comme une illustration parmi d'autres de la naturalité des divisions de temps que nous utilisons.

On peut remarquer au passage que cette structure présente une parenté intéressante avec le graphe associé au fameux « solide de Dürer », lui aussi à base « dodéca-cellulaire ».

 

 

 

                                                       

 

 

En version classique, ou « non cellulaire », le polyèdre dual du cuboctaèdre est le dodécaèdre rhombique, formé de 12 losanges, polyèdre lui-même remarquable en ce qu'il est, avec le cube, le seul polyèdre convexe à remplir à lui seul l'espace.

 

                      

 

Et on peut encore noter que c'est ce même dodécaèdre rhombique - du moins, sa moitié - qui sert aux abeilles à délimiter le fond de leurs galeries hexagonales, bien qu'il ait été démontré qu'il ne constituait pas (comme on l'a un temps supposé) la formule « la plus économique en cire », puisqu'il existait au moins une solution plus économique...

alvéole d'abeille à base hexagonale et à fond rhombique

 

 

 

Les diagrammes de Voronoï

 

Les diagrammes de Voronoï sont des structures logiques qui, à tout nuage de points du plan (appelés « germes »), répartis par hypothèse aléatoirement, associent une solution unique de pavage du plan par des polygones (« normalement » irréguliers). Pour les construire, rien de plus simple, on trace les médiatrices entre chaque point et ses voisins les plus proches, et on les interrompt... à l'endroit précis où elles rencontrent une autre médiatrice.

 

 

 

Comme la théorie des pavages cellulaires concerne précisément une série de problèmes qui se situent à l'interface entre la juxtaposition de cellules, d'une part, et la construction de pavages polygonaux ou polyédraux, de l'autre, les diagrammes de Voronoï ont, dans cette théorie, une valeur descriptive évidente. A ceci près que les réseaux cellulaires présentent, dans leurs diagrammes de Voronoï, une parfaite régularité qui n'est pas habituelle.

Il existe deux types de diagrammes de Voronoï pouvant être associés aux réseaux cellulaires, d'intérêt inégal : les diagrammes sphériques qui résultent de la projection de structures polyèdriques sur la sphère, et donnent une vision extérieure et en quelque sorte panoramique des réseaux cellulaires, et les diagrammes squelettiques, qui résultent, quant à eux, de l'analyse du réseau par des « coupes » bidimensionnelles transversales

Les diagrammes sphériques sont régis par la Loi de Bodart (que nous devons à une remarque de notre regretté ami Steven Bodart) :

Projeté sur la sphère, le dual d'un polyèdre cellulaire est son diagramme de Voronoï.

A partir de cette loi, toute solution de pavage cellulaire polyèdral de l'espace en 3 D peut être transformée en une solution de pavage de la sphère avec des tessons réguliers.

Par exemple, le dual du cuboctaèdre étant le dodécaèdre rhombique, au cuboctaèdre cellulaire élémentaire formé de 12 cellules groupées autour d'une treizième, correspond une solution de pavage de la sphère au moyen de 12 tessons en formes de losanges ; et ainsi des autres polyèdres cellulaires... - la remarque n'ayant, il est vrai, qu'un intérêt modeste, hormis peut-être esthétique.

 

 

Plus intéressants sans doute sont les diagrammes squelettiques, que nous nous contenterons d'introduire ici par un exemple « canonique », et qui « analysent », quant à eux la structure profonde d'un réseau cellulaire quelconque par des coupes bidimensionnelles transversales.

 

 

Diagramme de Barazzetti

 

 

 

 

 

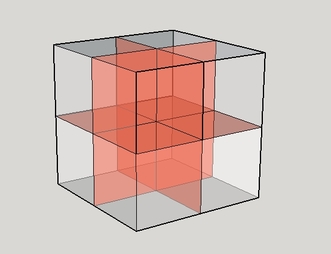
Si, dans un cube gnomonique de rang 2, on enlève l'ensemble de la surface extérieure pour ne laisser subsister que le squelette, ou la structure intérieure, (en rouge dans l'illustration ci-dessus), on obtient un diagramme de Barazzetti, structure qui, dans sa version euclidienne la plus simple, se présente sous la forme de trois plans sécants, centrés et orthogonaux entre eux, dont la jonction délimite 12 plans carrés identiques, (ou encore : trois carrés gnomoniques de rang 2).

 

diagramme de Barazzetti

 

  

Dans un cube gnomonique "discret" composé de 8 petits cubes détachables, les 12 plans du diagramme de Barazzetti correspondent aux zones de contact entre ces cubes.

 

 

 

A présent, si l'on examine à nouveau la structure du cuboctaèdre cellulaire (12 sphères groupées autour d'une sphère centrale) on s'aperçoit qu'il est possible de la construire de plusieurs manières différentes par des assemblages de polygones cellulaires. L'une des solutions les plus évidentes consiste, comme on l'a vu, à la décomposer en un hexagone « équatorial », complété à ses deux pôles par deux triangles, orientés l'un par rapport à l'autre, dans la position des deux triangles opposés du sceau de Salomon.

 

 

 

Mais une autre solution consiste à construire le cuboctaèdre au moyen de trois carrés cellulaires entrecroisés, que notre illustrateur de hasard a eu la magnanimité de distinguer ci-dessous par 3 couleurs différentes : bleu, blanc, rouge. Or que remarque-t-on dans cette configuration? Les 12 cellules du cuboctaèdre correspondent aux centres des 12 carrés du diagramme de Barazzetti. Autrement dit : le diagramme de Barazzetti n'est autre que le diagramme squelettique du cuboctaèdre.

 

 

                                                         

 

En effet, si l'on transforme les disques colorés du diagramme ci-dessous en des sphères de même diamètre et de même centre qu'eux, on retrouve les 12 cellules du cuboctaèdre.

 

 

Ce couple de structures remarquables : le cuboctaèdre cellulaire qui remplit optimalement l'espace avec de petites sphères, et son dual le dodécaèdre rhombique, qui remplit l'espace, « sort » donc immédiatement de la structure profonde du cube gnomonique de rang 2.

 

On nous permettra peut-être, pour l'occasion, de définir de manière volontairement un peu large le SQUELETTE LOGIQUE d'une structure quelconque, comme la partie de cette structure qui, amputée du reste, en conserve néanmoins les propriétés, ou le contenu mathématique essentiel.

Cette définition posée, on pourra remarquer que, de la même manière que le diagramme de Barazzetti est le squelette logique du cube gnomonique de rang 2, les 12 cellules du cuboctaèdre cellulaire sont le squelette logique du diagramme de Barazzetti.

Observation qui, rétrospectivement, semble justifier notre présupposé de départ, selon lequel les problèmes d'empilement compact et les problèmes de tessellation du plan ou de l'espace par des polygones ou polyèdres, gagnaient à être traités solidairement et d'une seule venue.

Les lois du gnomon sont une illustration de cette « corrélation ». On a vu dans d'autres articles que tout triangle gnomonique se transformait en carré gnomonique par une rotation de 180° des cellules monadiques qui sont ses triangles « pointe en bas », suivie d'une modification de 30° du paramètre angulaire ; logique dans laquelle les polygones atomiques, ou élémentaires, sont considérés comme des cellules souples, qui se « solidifient », ou se résolvent en différents « diagrammes de Voronoï », en fonction des positions relatives de leurs centres à tout instant du processus.

 

Dans cette représentation, l'état cellulaire correspond donc à une phase intermédiaire, ou de transition, entre différents systèmes de pavage polygonaux ; et de ce fait il apparaît comme plus fondamental, ou plus originaire ; - à l'image du paradigme cristallin, où ce sont des arrangements de "points" microscopiques, les atomes, qui par leur répétition, produisent à grande échelle des arêtes et des angles parfaitement "clivables", délimitant de parfaits polyèdres.

 

 

CONCLUSIONS

 

Quelques esprits froids pourront nous objecter que, par ces détours, nous n'avons fait que redécouvrir l'eau tiède de ce qu'est « un réseau cubique à faces centrées » . Tout bien réfléchi, nous nous en contentons. Dans un domaine aussi balisé que celui de la symétrie, il n'était pas question d'apporter ici ce qu'on entend par des « nouveautés mathématiques » ; il nous suffit que, chemin faisant, cette étude ait pu contribuer à apporter un peu d'ordre dans la formulation d'un problème logico-mathématique assez général, celui de la reproduction d'objet, où il n'en existait aucun... - symptôme d'une tendance de l'esprit mathématique, qui, à force d'habitudes généralisatrices, en est peut-être venue à être saisie d'un doute sur l'existence même d'objets mathématiques...

L'intérêt de l'approche quadridimensionnelle pythagoricienne réside, croyons-nous, dans le contraste entre la richesse des contenus de science que l'on est conduit à développer pour une compréhension suffisante des notions engagées, et l'étonnante simplicité de l'appareil logique grâce auquel on y parvient ; - puisque l'ensemble de ces structures mathématiques relativement complexes est construit ici, rappelons-le, au moyen d'objets tels que celui-ci :

   

 

 29 MAI 2016

 

 

 

ANNEXES

 

 

I

 

Comment calculer facilement le rang et la valeur d'un polyèdre cellulaire d'après son aspect extérieur, et comment déterminer la valeur du polyèdre supérieur à un polyèdre donné.

 

On a vu que le rang d'un objet cellulaire quelconque se calculait par un moyen très simple : côté -1 pour les polygones, arête -1 pour les polyèdres. Quelques recettes permettent ensuite d'en déduire le nombre total de cellules, pour tout polyèdre.

Tétraèdre.

Le tétraèdre élémentaire, formé de quatre cellules, se reconstitue par l'ajout, à sa base, de triangles cellulaires, dont la progression correspond à celle des nombres triangulaires supérieurs à trois : 6, 10, 15...

Cube.

La série des cubes cellulaires est construite sur le même modèle que celle des cubes gnomoniques - à la réserve qu'elle débute avec un rang de décalage - puisqu'elle correspond à la série des cubes des nombres entiers naturels supérieurs à 1 : (8, 27, 64, 125....)

Octaèdre.

Tout octaèdre a pour plan de symétrie un carré cellulaire. Pour construire l'octaèdre de rang supérieur, on ajoute à l'octaèdre de base : ce même carré cellulaire + le carré cellulaire de rang supérieur.

Par exemple, l'octaèdre atomique, composé de 6 cellules, a pour plan de symétrie un carré cellulaire de 4 cellules. Pour construire l'octaèdre supérieur, on lui ajoute un carré de 4 cellules + le carré de rang supérieur, composé de 9 cellules. L'octaèdre de rang 2 se compose donc de : 6 + 4 + 9 = 19 cellules.

Cuboctaèdre.

Pour le cuboctaèdre, c'est à peine plus compliqué. L'illustration ci-dessous indique la série des compléments qui doivent être ajoutés au cuboctaèdre de base, composé de 13 cellules, dont on voit qu'ils suivent la progression : (42, 42 + 50, 42 + 50 + 70, 42 + 50 + 70 + 90...) et ainsi de suite.

 

 

 

 

II

 

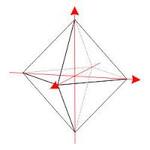
Le vecteur d'équilibre de Buckminster Fuller

 

Richard Buckminster Fuller a attribué au cuboctaèdre divers noms tels que "vector equilibrium", "heléfantaèdre" ou "dymaxion".

Le cuboctaèdre est le seul polyèdre semi-régulier dont la distance du centre de gravité aux sommets est égale aux arêtes. On a donc au total 36 vecteurs isométriques, 12 pointant du centre aux sommets, en relation angulaire constante (60° partout), et 24 correspondant aux arêtes. Ce nombre s'élevant même à 72, si l'on prend en compte les vecteurs opposés.

 

 

 

Si ces propriétés sont bien connues, Buckminster Fuller est le premier à avoir saisi leur profond intérêt physique. 

Cette situation d'équilibre vectoriel parfait peut être comparé à celle d'une bulle de savon en train d'être gonflée. La bulle tend à conserver sa forme sphérique à quelque échelle que ce soit : ici en raison de la tension de surface. Dans le cuboctaèdre, la croissance d'un vecteur pointant du centre à l'un des sommets, (égal au rayon de la sphère circonscrite), détermine la croissance isométrique et simultanée des 35 autres rayons et arêtes qui constituent avec lui l'ensemble de la structure, laquelle peut ainsi augmenter de façon continue "sans que rien ne semble se passer". Dans les deux situations, l'équilibre est parfait, parce que la tension est égale en tout lieu.

Buckminster Fuller compare cette situation à deux réalités qu'il est très important de comprendre dans un sens pleinement physique, si l'on ne veut pas s'égarer dans des interprétations poétiques : le silence, d'une part (où l'équilibre  énergétique parfait est assimilé à l'absence totale de résonance); et le vide d'autre part, au sens d'une pure "virtualité" d'espace, non encore déterminée, ou encore, au sens d'un atome ou d'un grain d'espace.

"Le Vector Equilibrium est le point zéro de départ pour tout événement ou non-événement : c'est le théâtre vide et le cirque vide et l'Univers vide qui est prêt à montrer n'importe quelle action à n'importe quel public". (R. Buckminster Fuller)

De fait, les propriétés de ce "vecteur d'équilibre", formé de la somme nulle de 72 vecteurs, s'apparentent à celles du point "euclidien" sans dimension, dépourvu de métrique, qui n'a en soi de réalité que comme condition d'existence (et plus précisément : condition aux limites ou au bord) d'un hypothétique objet géométrique, resté lui-même non défini, ou à définir.

 

 

 

 III

 

Cosmologie de Pétron et Lambda de Platon

 

On a vu que le pavage hexagonal d'échelle 5 imaginé par Torres-Heredia Julca fournissait une explication très séduisante des "183 mondes, disposés sur un triangle" évoqués dans la cosmologie de Pétron d'Himère. 

 

                                                         

 

A partir des "183 mondes disposés sur un triangle", correspondant dans cette hypothèse au Cosmos de Pétron, on obtient, par "dupli-rotation" (duplication + rotation de 180° de l'élément dupliqué), la structure en sceau de Salomon formée de "366 monades, disposées sur un hexagone", qui correspond quant à elle à l'Année dans le pavage de Torres-Heredia Julca :

 

                                                      

 

On a remarqué aussi que ce pavage d'échelle 5, muni de ses compléments latéraux, pouvait s'analyser comme la somme de 54 tétractys + les 7 points générateurs au centre des hexagones 61. Ces nombres 54 et 7 ne peuvent manquer de nous faire penser au Lambda de Platon, structure formée de 7 nombres, dont la somme égale 54.

Cette coïncidence pourrait suggérer la possibilité d'une origine commune aux cosmologies de Pétron et de Timée; sinon même, l'hypothèse que toutes deux ne soient que les résidus d'un même ensemble théorique originel, plus complet.

 

                                                     

 

On va voir que ce rapprochement peut être poussé un peu plus loin.

En effet, si l'on additionne les nombres du Lambda dans l'ordre naturel, on constate qu'ils se répartissent en trois sous-ensembles, dont la somme est à chaque fois un multiple de 6.

54 = (1+2+3) + (4+8) + (9+27)

Or ces différentes sommes inférieures correspondent, par une coïncidence assez remarquable, à trois régions, trois ensembles topologiques distincts du pavage hexagonal :

(1+2+3) = 6         =      les 6 tétractys blanches qui composent l'hexagone central

(4+8) = 12            =      les 12 tétractys blanches qui composent les "compléments latéraux"

(9+27) = 36         =       les 36 tétractys colorées qui correspondent au "calendrier annuel"

Envisagé sous cet angle, le Lambda de Platon semble donc fournir un formulaire arithmétique pour la construction, comme pour la description du pavage; mieux, il paraît même contenir une recommandation implicite sur les différences de couleur à exprimer.

 

 

 

 

IV

 

Vues cavalières

 

La collection de manuscrits ésotériques de Manly Palmer Hall (1500-1825) conserve deux dessins représentant des diagrammes de Barazzetti en perspective cavalière, vus suivant la diagonale du cube gnomonique associé, de manière à former des "sceaux de Salomon". La même idée est illustrée avec des diagrammes de types "plein" et "vide".

                                    

                                            

 

Le dessin de gauche présente, en son milieu, une figure composée de trois losanges "vesica piscis" (formés de deux triangles équilatéraux), compris dans un hexagone : figure qui, en perspective, présente elle aussi une "ambivalence" du même genre, puisqu'elle peut être vue soit comme un cube, soit comme un dodécaèdre rhombique. "Le dodécaèdre rhombique pose des problèmes de vision dans l'espace, car lorsqu'on le regarde suivant une diagonale, on a l'impression de voir un cube." (Robert Ferréol, Mathcurve).

 

Dans le dessin de droite, on remarque que le sceau de Salomon lui-même peut s'analyser comme la superposition de trois losanges "vesica piscis", disposés en étoile.

 

(R. B, G. D)

 

 

 

V

 

Les objets cellulaires en équations

par R. Bayoud

 

J'appelle "coeur" le point central de rang 0 (hors-jeu si tu veux), autrement dit c(0) = 1

J'ai ensuite calculé le nombre d'éléments pour chaque "couche" c(n)

"figure(n)" correspond au total des éléments depuis le coeur jusqu'à la couche n : somme de 0 à n des c(k)

 

point(n) = 1

segment(n) = 1 + n

triangle(n) = ( 2 + 3n + n² ) / 2

carré(n) = 1 + 2n + n²

hexa(n) = 1 + 3n + 3n²

cube(n) = ( 2 + 3n + 3n² + 2n³ ) / 2

tetra(n) =  ( 12 + 22n + 12n² + 2n³ ) / 12

octa(n) = ( 3 + 7n + 6n² + 2n³ ) / 3

cuboc(n) = ( 6 + 22n + 30n² + 20n³ ) / 6

 

Voilà pour les formules particulières.

Le développement des polynômes (de 1 à 4 termes) correspond à la position des objets sur "l'échelle" quadridimensionnelle. Du coup : chaque figure peut être vue comme un accord musical, dont les intervalles sont réglés par son polynôme. (Et comme on prend des ratios ça élimine le problème du dénominateur des fractions.) Pour les solides où les polynômes sont de la forme : a + b.n + c.n^2 + d.n^3, on peut ainsi théoriquement construire les intervalles : b:a, c:b et d:c, les 3 ensemble formant un "accord". 

Quant à la formule génératrice de toutes les suites, elle me semble hors d'atteinte pour le moment.

La seule chose relativement évidente c'est qu'il s'agit d'un polynôme de coefficient fixe = 1 et de degré égal à la dimension impliquée.

 

 

 

 

 REFERENCES :

 

Un lien géométrique entre le cercle et le système sexagésimal, Jaime Vladimir Torres-Heredia Julca, 2005.

La plaine de vérité, Dom Néroman, Arma Artis, 2009.

L'espace symbolique, Enrico Barazzetti, Archè, 1997.

Automates cellulaires et pavages vus comme des réseaux booléens, Hussein Ben-Azza, thèse de doctorat en informatique, sous la direction de Jacques Mazoyer, Lyon I, 1995.

 

 

 

 

 

 

 

 

LAMBDA DE PLATON

et cubes gnomoniques de rangs 2 et 3

 

 

 

par G. Denom

 

 

 

 

 

Deux forces règnent sur l'univers : lumière et pesanteur.

Simone Weil

 

 

 

 

 

 

 

 

Le principe gnomonique de la musique pythagoricienne

 

 

Stephen Phillips a consacré, sur son blog, une étude géométrique intéressante au lambda platonicien (timéen pour d'autres), à voir ici, qui identifie dans cette structure l'interface arithmétique commune à la théorie musicale pythagoricienne et à ce qu'il nomme avec d'autres les "géométries sacrées"; même si nous devons confesser que cette expression n'a pas, pour nous, de signification bien évidente en pythagorisme, dans la mesure où, selon cette doctrine, c'est la géométrie elle-même qui peut être considérée comme "sacrée", ou, du moins, toute géométrie peut l'être, si elle est envisagée sous l'angle adéquat. Aussi, s'agissant de géométries issues des spéculations symboliques de différentes traditions ésotériques, telles que le yi king, l'arbre de vie ou le sri yantra, il nous semble suffisant de parler de géométries ésotériques, ou traditionnelles; avec l'avantage d'éviter ainsi, peut-être, le soupçon d'aller trop vite en besogne, et de présenter comme acquis, ou assuré, ce que l'on se propose en l'occurrence d'établir, ou d'illustrer.

 

La structure du lambda de Platon est morphologiquement analogue à celle de la dyade indéterminée, comme à celle du tenseur binaire radical de la linguistique guillaumienne. L'analogie ne se limite pas à une question de forme, puisque les deux jambes du lambda, constituées par le développement quaternaire, ou "tétractyque", en tant que rapporté à l'unité originaire, des carrés et des cubes des nombres 2 et 3, correspondent aux tensions "binaire" et "ternaire" du tenseur linguistique, à ceci près que, dans la topologie véritablement génétique de ce dernier, comme un peu partout dans la tradition pythagoricienne, la tension ternaire ou impaire, considérée comme fermante, (et correspondant à la catégorie du Même), précède la tension binaire ou paire, considérée comme ouvrante, (et correspondant à la catégorie de l'Autre) : ordre que l'on retrouve aussi bien dans la tension cosmologique empédocléenne, que dans la "table des opposés" d'Alcméon de Crotone.

 

 

                               

 

Point-atome : 1                                     Point-atome : 1

Arête-segment : 2                                Arête-segment : 3

Face : 4                                                 Face : 9

Volume : 8                                             Volume : 27

 

La musique pythagoricienne, comme on le voit, est construite avec de simples cubes. En effet, la jambe droite (ci-dessus) du lambda nous renvoie, exemplairement, aux valeurs du cube gnomonique de rang 3, comme le rubix-cube, dans lequel les nombres : 1, 3, 9 et 27 correspondent à l'atome-graine (point), à l'arête (segment), à la face (surface) et au volume du cube respectivement. Quant à la jambe gauche du lambda ci-dessus, elle n'évoque pas seulement les valeurs du cube gnomonique de rang 2 (où 1 = point-atome-graine, 2 = arête, 4 = face, 8 = volume), mais aussi bien certains processus sphériques, tels que celui de la division cellulaire, de la monade biologique.

 

 

 

Le cube gnomonique de rang 2 et la monade biologique

 

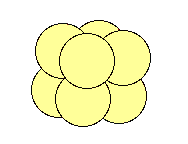
embryon au stade de 8 (x1) cellules, réparties en 2 hémisphères de 4 cellules

 

Il peut être intéressant de s'attarder un peu sur cette monade biologique, à ce stade de développement précoce où elle correspond au cube gnomonique de rang 2, car on constate qu'elle y est déjà dotée d'une structure tridimensionnelle, et que les principaux axes de symétrie de l'individu sont, eux aussi, déjà définis. 

Du point de vue monadologique, les trois axes de symétrie majeurs de la monade (l'un vertical, les deux autres horizontaux), correspondent aux "trous" ou aux interstices entre les cellules, mais aussi à l'historique de leurs mouvements relatifs; tandis que, d'un point de vue rétrospectif, ces trois mêmes axes fondamentaux déterminent l'emplacement des parois intérieures ou des surfaces de contact entre les cellules. Or, si la monade-point est déjà divisée en deux au stade du segment ou du "filament", elle se retrouvera, inévitablement, divisée en quatre au stade du plan ou de la "membrane" (disque), et en huit au stade de la cellule formée ou de la sphère (boule), puisque, du point de vue topologique, chacune de ces structures est formée ici par une duplication de celle qui la précède.

Le disque horizontal de la monade étant, structurellement, formé de deux segments entrecroisés, il est nécessaire qu'il corresponde à quatre points-éléments, et donc quatre "quartiers".

 

Mais d'autre part, le plan de l'horizon étant, par définition, décalé de 90 degrés par rapport au segment vertical de référence, et les deux segments composant la croix horizontale étant le lieu d'une intersection avec la dimension verticale, il est nécessaire que, dans cette dimension, il existe deux plans, deux disques identiques au disque de l'horizon, et perpendiculaires entre eux comme à ce dernier.

 

 

Dans la situation finale de l'orange biologique, il subsiste donc trois plans : un plan horizontal et deux plans verticaux, l'un frontal et l'autre sagittal, qui définissent huit (8) demi (1) - quartiers (4) répartis en deux hémisphères (2) de part et d'autre du plan horizontal de référence : - où nous retrouvons, dans leur expression naturelle, tous les nombres de la jambe gauche de notre lambda, structurellement identiques aux coordonnées intérieures d'un cube gnomonique de rang 2, comme dans la situation de ce personnage :

 

Chacun des trois plans générateurs étant divisé en quatre, on a au total 12 plans qui correspondent à l'ensemble des surfaces du cube gnomonique qui sont en contact avec une autre. La transformation du cube gnomonique de rang 2 en monade biologique sphéroïdale s'effectue simplement en remplaçant les trois carrés gnomoniques générateurs (CG de rang 2) par des cercles, ou plus exactement des disques.

 

Vision artistique de la monade biologique, à la structure formée de trois disques concentriques et perpendiculaires les uns aux autres, avec ses trois axes de référence.

 

En vertu des lois de la tension superficielle, les parois internes, aussi bien que l'enveloppe de la cellule, peuvent être recréés de manière très simple au moyen de trois anneaux assemblés sur les trois axes de la monade (composant un chrisme tridimensionnel), et de bulles de savon.

Pour une raison circonvoisine, (puisque l'octaèdre est la structure duale du cube), l'octaèdre - polyèdre à (8) x (1) faces - inscriptible dans la sphère, composé de deux pyramides (2) à base carrée (4) opposées, et dont les coordonnées des 6 sommets sont définies par les trois axes directeurs de la monade, est, du point de vue physique qui est celui de l'équilibre des vecteurs, la plus stable des structures spatiales issues de la théorie pythagoricienne des solides.

 

 

  

 

De fait, il est possible de construire un octaèdre évidé, ou réduit à l'état de squelette, au moyen de l'entrecroisement de trois carrés, dans lequel aucune des propriétés essentielles de ce solide n'est perdue; et ces trois carrés correspondent aux trois carrés gnomoniques de rang 2 qui définissaient, précédemment, les parois intérieures du cube gnomonique de rang 2, comme ils correspondent aux trois disques de la monade biologique.  Il est également possible de construire cette figure avec huit tétraèdres irréguliers dont les bases sont des triangles équilatéraux et les trois autres faces des triangles isocèles rectangles.

 

 

 

 

 

Tension binaire et tension ternaire : deux forces physiques très concrètes

 

 

Cette parenthèse refermée, on pourra résumer ce qui précède en disant que les deux jambes du lambda nous représentent les propriétés de développement gnomonique propres aux nombres monadiques 2 et 3, dans leur rapport conjoint à l'unité cardinale, et sous la définition spatiale quadridimensionnelle qui est spécifiquement la leur dans la mathématique pythagoricienne.

A présent, comment caractériser la différence entre les deux systèmes, - entre les deux jambes du lambda?

Dans un cube gnomonique de rang 2, le centre de symétrie n'est pas un élément du système.

Si la tension paire, la tension binaire, est considérée comme ouvrante ou centrifuge, c'est parce qu'elle a pour centre géométrique un vide séparateur. Dans l'ordre des interactions physiques, la tension binaire est donc associée à la force électromagnétique et, caractéristiquement, à la lumière, comme en général à tout phénomène de rayonnement; - force dans laquelle, à tous les étages d'observation, la bipolarisation semble être une propriété "immanente". Si la lumière est ce qu'il y a de plus rapide, c'est parce qu'elle est ce qui "fend" et divise le mieux l'espace. A une autre échelle, la tension binaire pourrait aussi être associée au phénomène de la fluctuation quantique, propriété essentielle du vide, productrice de paires de particules.

A l'inverse, dans un cube gnomonique de rang 3, le centre de symétrie est un élément du système, celui des 27 petits cubes qui est situé au centre de celui-ci, autour duquel un plus grand cube est construit de manière continue, à la manière d'un fruit autour de son noyau, (ce qui en fait une représentation achevée, car tridimensionnelle de la dyade indéterminée), et vers lequel convergent l'ensemble des segments ternaires particuliers dont est constitué le cube. Le véritable gnomon (tridimensionnel) du cube peut donc, à cet égard, être regardé comme un ensemble sphéroïdal d'une seule pièce, constitué de 26 éléments groupés autour d'un noyau. Si la tension impaire, la tension ternaire, est considérée comme centripète ou fermante, c'est parce qu'elle a en son centre un être positif, qui est en même temps un attracteur. Dans l'ordre des interactions physiques, la tension ternaire est donc associée à la force gravitationnelle, comme l'illustre exemplairement le problème à trois corps.

Si la tension ternaire précède logiquement la tension binaire, c'est parce qu'un être précède, logiquement, la possibilité qu'il a d'être coupé en deux; c'est parce que, pour que puisse être coupé en deux quelque chose, il faut qu'il y ait quelque chose. La tension ternaire a pour centre la monade cardinale, l'objet, tandis que la tension binaire a pour nature profonde la nature du couteau. Or c'est l'être qui tient le couteau, et non le couteau qui tient l'être.

Il n'y a sans doute pas d'autre force agissante dans la nature, que ces deux forces dont les effets sont connus et visibles à l'échelle humaine : celle qui fait choir une pomme à terre, et celle qui fait jaillir la lumière d'une lampe électrique. Dans la mesure où, selon le principe sain de la physique, une force se connaît à ses effets, les forces nucléaires faible et forte, dont les effets, annihilés à notre échelle, nous sont invisibles, puisqu'elles sont confinées dans le noyau de l'atome, où elles n'entrent en jeu que pour faire tenir ensemble des composants élémentaires qui, sans elles, ne s'accorderaient pas, n'ont assurément pas le même statut scientifique, et nous renseignent sans doute davantage sur les limites actuelles de nos théories, sur notre connaissance insuffisante de la délicate horlogerie selon laquelle les forces fondamentales peuvent se combiner à l'échelle subatomique, que sur la nature des choses. On peut déjà remarquer que les forces nucléaires "faible" et "forte" ne sont, par leurs noms mêmes, pas associées, comme les deux précédentes, à une multiplicité d'effets micro, méso et macroscopiques, mais à un topos bien défini qui est le noyau de l'atome, or il est singulier et scientifiquement inhabituel que les effets d'une force physique, et a fortiori d'une force universelle, soient assujettis et limités à un topos particulier; car le noyau de l'atome n'est qu'un lieu aussi déterminé de la nature que peut l'être la coquille d'un oeuf, et par conséquent lorsqu'on parle de forces nucléaires forte et faible on ne dit, scientifiquement, rien de plus impressionnant que "la petite et la grosse force de la coquille", qui sont précisément les deux dont vous avez besoin pour que votre coquille n'explose pas. Mieux vaudrait, peut-être, s'interroger sur ce que l'on a mis dans l'oeuf. Rien de commun, donc, avec des forces universelles dont les effets directs se diffusent réellement à de multiples niveaux d'observation de la nature, comme celles que nous évoquions au début de ce paragraphe, savoir : la gravitation et la force électromagnétique.

Si nous pensons que deux tensions sont suffisantes pour expliquer ce qui se passe dans le monde physique; c'est parce que nous avons  constaté que deux tensions étaient habituellement suffisantes, pour expliquer ce qui se passe dans le monde mathématique. On peut sans doute dire que si un problème ne relève pas de l'une de ces tensions, il ne relève pas de la mathématique; car nous ne parvenons pas à concevoir une forme de tension, opératoire en mathématique, et ayant donc un sens pour cette science, qui ne procède pas de l'un ou l'autre de ces archétypes, relevant des propriétés universelles de la dyade indéterminée, ou qui n'en dérive par composition. Or concernant maintenant les possibilités d'explication propres à la science physique, nous pensons qu'une explication physique ne sera jamais satisfaisante pour l'esprit, si elle ne s'achève pas dans une représentation du genre mathématique; cette affirmation qui pourrait presque apparaître comme un cliché ou une généralité creuse, ne l'est pas en réalité pour nous, puisqu'elle revient à rappeler la science aux sources pythagoriciennes de son inspiration première, au prix d'un petit effort pour enjamber cet autre cliché, selon lequel en pythagorisme "tout est nombre". La "mathématique pure", en tant que science des possibilités a priori de l'être, sera toujours légitime à s'exprimer en science physique, dans la mesure où la science physique elle-même ne se reconnait pas d'autre garant, n'admet pas d'autre genre de monstrations et de preuves, que celles que lui apporte la mathématique. Et ce, bien que depuis Galilée, cette mathématique pure en soit finalement venue à être regardée comme un instrument abstrait et froid, dont l'usage ne se justifie, au fond, qu'à raison de ses succès pratiques en terme de prédiction et de calcul.

 

 

Même - Autre, Un - Multiple

derrière ces catégories dialectiques : deux constantes cosmologiques

 

 

Ces forces physiques bien connues et manipulables à l'échelle humaine, sont aussi manifestes à une échelle supérieure; puisque c'est à elles que se résume l'activité apparente du ciel. 1. Les astres gravitent et 2. émettent des rayonnements, des ondes, au premier rang desquels la lumière. Si la lumière est ce qu'il y a de plus rapide, c'est parce qu'elle est l'être dont la tendance naturelle, le vecteur, est le plus opposé à celui de la gravitation; en tant que limite constante du système cosmologique, elle représente donc à cet égard un extremum, un correspondant polaire à la gravitation. Si la gravité est ce qui fait que toutes choses se dirigent du même côté (ou du côté du Même), la lumière est ce qui se rend le plus vite de l'"autre" côté, (ou du côté de l'Autre). Ce n'est pas sans raison que le nom de la tétractys désigne par le mot "rayon" ce qui est en fait une dimension mathématique, et pas seulement d'espace, mais d'espace-temps. Certes une réalité mathématique est nommée ainsi au moyen d'une analogie physique; mais l'important est qu'il s'agit en l'occurrence d'une analogie correcte.

A l'inverse, nous voyons avec les trous noirs que, lorsque la gravité d'un astre est excessive, les rayonnements de la lumière sont non seulement piégés et emprisonnés dans cet astre, mais littéralement aspirés dans une direction inverse de celle qui est naturellement la leur, qui est celle de la singularité et du point; de sorte que les vecteurs d'extension de la lumière qui étaient précédemment des vecteurs de division de l'espace macroscopique, doivent à présent être des vecteurs de division de l'espace microscopique, de la dimension du point, elle-même d'extension indéfinie. Et il est remarquable que la monade biologique puisse être considérée en même temps de ces deux manières : comme un problème de division d'une singularité primordiale, et comme un processus de croissance ou de développement de l'individu. Cela montre que la cellule vivante relève d'un accord ou d'un équilibre entre deux tendances essentiellement contraires.

*

Dans la tradition pythagoricienne, il est dit que le monde résulte d'un accord, d'une harmonie, ou d'un mélange, entre ces deux tensions contraires, appelées "même" et "autre", - qui ne sont pas seulement des agents logiques, comme on l'a généralement cru à tort, mais aussi des forces physiques très concrètes, l'une "rentrante" , l'autre "sortante", l'une aspirante ou "siphonnante", évoquant un entonnoir ou un vortex, l'autre émanante ou rayonnante. C'est dans la connaissance de cette harmonie, de cet accord intime de la nature, que consiste l'art pythagoricien de la musique des sphères, dont le Timée offre l'exemple le plus connu. Toutefois, si dans le domaine purement mathématique qui est celui de la théorie musicale, l'harmonisation de ces deux systèmes, binaire et ternaire, peut s'effectuer au moyen des trois seules médiétés classiques : arithmétique, géométrique et harmonique, qui forment du reste un tout logique, il n'en va pas de même dans le domaine des sciences de la nature, où une quatrième médiété entre en jeu : la médiété Nicomaque 10. Or, de ces deux plans ontologiques, le plan mathématique et musical, et le plan de la science physique, le second est plus développé et plus complet, puisqu'il inclut le premier comme partie, comme noyau mathématique, tout en le développant selon une modalité particulière d'existence, qui est celle, en l'occurrence, de notre univers physique. Entre les deux, il y a toute la différence qui existe entre la simplicité de la tétractys, et la richesse du monde physique, entre les conditions de possibilité de la forme, et la réalisation d'une forme particulière. Le problème du Timée de Platon est qu'il semble avoir tenté de réunir dans un récit continu, en fonction d'analogies trompeuses, des considérations qui, à l'origine, relevaient de plans ontologiques différents; de sorte que la seule façon d'en user avec ce texte semble être d'en considérer les morceaux isolément, comme les pièces d'un puzzle incomplet en l'état, comme on le fait d'ordinaire pour le reste de la tradition pythagoricienne. Ces réserves faites, il importe surtout de souligner que les tensions binaire et ternaire du lambda de Platon correspondent, de façon parfaitement évidente, aux deux tensions fondamentales de la cosmologie empédocléenne; ou encore, pour enfoncer ce clou, la dialectique du Même et de l'Autre ne présente aucune différence avec celle, empédocléenne, de l'Un et du Multiple, la seule différence consistant dans le choix d'un couple d'agents logiques dans le premier cas, et mathématiques dans l'autre; mais cette différence ne signifie en l'occurrence rien de plus, que le fait que la réalité elle-même puisse être envisagée de manière alternative sous ces deux aspects, sans cesser d'être une et la même; de sorte que, malgré le déni de la critique historique et philosophique à ce sujet, on est contraint d'admettre qu'il y a, entre ces deux monuments de l'ancienne physique pythagoricienne, un accord absolu sur les principes, comme il est naturel et inévitable dans toute tradition qui se respecte, même s'ils diffèrent dans la façon de les appliquer.

*

 

Du point de vue strictement physique, il n'existe sans doute que deux constantes véritablement universelles : la constante gravitationnelle et la vitesse de la lumière; toutefois un univers gouverné par ces deux seules constantes serait, selon toute vraisemblance, incapable de faire naître quelque chose, si une troisième constante n'intervenait dans le processus, celle-là d'essence mathématique : la constante phi, pour des raisons qui ne pourront ici qu'être effleurées.

Sur le plan ontologique particulier qui est celui de la Nature, toute existence individuelle repose, du point de vue topologique, sur une assise en forme de double spirale, l'une rentrante, l'autre sortante, spirales qui, en arrivant au contact l'une de l'autre à partir de vecteurs opposés, agissent l'une à l'égard de l'autre comme des freins, et forment donc une médiation entre deux tendances de la nature, l'une centripète, l'autre centrifuge, qui l'une comme l'autre, sans cette médiation conduiraient cette existence individuelle à disparaître physiquement. L'existence individuelle d'un être naturel est donc conditionnée à celle d'une "matrice" topologique, capable de freiner les forces universelles qui le traversent, en fonction d'un milieu qui est, pour cet être donné, celui de sa survie, de sa continuité dans le temps, mais qui est aussi une réelle position et une coordonnée mathématique, ou plus exactement un système à deux coordonnées, composé d'un centre et d'un environnement, (selon les deux sens que revêt en français le mot "milieu", compris ici synthétiquement); - freiner ces forces, sans toutefois les stopper complètement, sans quoi aucun mouvement, ni aucune existence individuelle ne serait possible.

 

 

Le problème topologique de la monade-univers, autrement appelée Nature. Le Mélange et l'Harmonie : le "frein à main" de la nature universelle.

 

Pour se donner une idée du problème, on peut se représenter, par exemple, l'action que les tensions binaire et ternaire exercent sur un objet comme le segment; en ayant à l'esprit le fait que le segment n'est qu'un état, et donc une représentation particulière de la monade, et qu'à cette réserve, les choses ne doivent pas se passer de manière très différente pour la monade-univers. La tension ternaire centripète détermine le segment à se contracter en direction d'un point qui est son centre, afin de continuer à ne former qu'un seul objet. La tension binaire centrifuge le détermine à se séparer en deux parties égales, dont chacune se précipite dans une direction opposée à celle de l'autre. Cependant, en l'état, il ne peut rigoureusement rien se produire, puisque les deux forces s'annulent. La deuxième force voudrait que le segment se brise en son milieu, qui est précisément le lieu où la première force, la force ternaire unifiante, a son foyer. C'est ce qu'exprime le Timée lorsqu'il affirme que "le même et l'autre sont rebelles au mélange". Pour qu'il se passe quelque chose, pour qu'une existence individuelle puisse se manifester, les deux tensions, centripète et centrifuge, doivent s'harmoniser selon deux spirales symétriques, (que l'on pourrait comparer, topologiquement, à la double hélice de l'ADN), l'une rentrante, l'autre sortante, orientées en sens inverse l'une de l'autre, et attachées l'une à l'autre par des coordonnées d'intersection régulières, constituant des foyers de discrétisation, jusqu'à former, si l'on veut, pour nos deux forces, un dispositif de décélération et de neutralisation mutuelle progressive. A ces spirales, finalement réduites à une seule structure, correspond un certain logos, un certain rapport - ou une médiété - entre trois termes, dont chacun (hormis le premier) est à chaque fois le médian de deux autres, qui permet à cette spirale de se dérouler sous la forme d'un escalier discret où, à chaque pallier, se forment certaines catégories de monades. Or, dans le plan ontologique particulier qui est celui de la nature et de la science physique, la médiété qui possède, à l'égard de ces deux tendances fondamentales (et "destructrices" si on les considère individuellement) de la création, la valeur de zéro logique ou de diagonale, et que l'on peut donc considérer comme la position idéale du "frein à main" de la nature universelle sur une échelle graduée; - comme la position qui s'avère, à tous les échelons de celle-ci, génératrice de centres d'accrétion, de "stoppages", d'existences individuelles stables telles que : galaxies, étoiles, planètes, êtres vivants, en un mot comme en cent de monades ou de points, et qui semble par là pouvoir être rapportée au concept, pour nous étymologique, de la Nature comme naissance, engendrement universel, comme à celui plus mathématique de formation; -  cette médiété n'est autre que la médiété Nicomaque 10 ("de Fibonacci"), tendant vers le nombre d'or,  dans laquelle (c-b)/(c-a) = a/b, comme nous espérons le montrer un jour de façon plus détaillée. Sachant que, ce qu'il importe de comprendre en l'occurrence, c'est pourquoi, quand on divise un segment dans le rapport d'extrême et moyenne raison, on ne fait pas seulement de la mathématique, mais aussi de la physique, et ce, à presque tous les étages de cette science; c'est en tous cas le point sur lequel la recherche contemporaine devrait concentrer son attention.

En tant qu'elle fait revivre sous nos yeux, dans sa richesse, l'ancien concept grec de la Nature et de la science physique, science qui se présente d'emblée sous une variété de niveaux et de catégories, mais néanmoins non morcelée, car réunie par un principe transversal, la problématique du nombre d'or a sans doute aussi quelque chose à voir avec un enjeu historique propre à la science occidentale, qui est celui de la réunification de la science physique, ainsi qu'avec l'émergence de nouvelles générations de physiciens, moins spécialisés que ne l'étaient leurs prédécesseurs.

 

*

 

Les forces à l’œuvre dans le secret de l'atome, doivent être les mêmes que celles qui ébranlent la machine du ciel. "Ce qui est en bas est comme ce qui est en haut". Du moins ce chemin est-il le seul qui mérite le nom de science.

 

 

 

Le 10.09.2014

 

 

 

 

ANNEXE

 

 

L'univers a-t-il la structure d'un chou romanesco?

 

 

 

Le nombre d'or n'est pas le fait d'une imagination mathématique mais le principe naturel des lois de l'équilibre.

R. A. Schwaller de Lubicz 

 

 

 

 

 

Selon les données pythagoriciennes que nous venons de développer, la structure de l'univers pourrait être comparée à celle d'un chou romanesco, - structure géométrique à laquelle conviendrait particulièrement, comme on va le voir, le surnom de "mont analogue".

 

 

La structure générale du chou est celle d'un cône, qui est l'expression tridimensionnelle la plus simple de la dyade indéterminée. Le sommet du cône correspond au foyer originaire de la force gravitationnelle, et sa base ou son "embouchure" inférieure, aux limites d'expansion de la force électromagnétique.

Le cône est sillonné par des spirales de Fibonacci rayonnant à partir de son sommet, les unes "lévogyres", les autres "dextrogyres", (habituellement 8 et 13, soit deux nombres successifs de Fibonacci); et sa surface se compose, endomorphiquement, d'innombrables cônes de tailles différentes, tous semblables au plus grand, et eux-mêmes constitués de cônes plus petits, ad perpetuum. Chacun de ces cônes inférieurs, définis par l'intersection de deux spirales antagonistes, correspondant à un "stoppage", à un foyer d'accrétion ou de "retombée" gravitationnelle, et donc à une division ponctuelle et monadologique de l'univers telle que : amas, galaxie, système solaire, planète, être vivant, etc.

Cette structure est abusivement qualifiée de "fractale" alors qu'elle est rigoureusement gnomonique, puisque les spirales sont construites au moyen de rectangles de Fibonacci, et donc de carrés gnomoniques. Or à la différence de la "théorie" des fractales qui n'est qu'une collection de faits mathématiques assez vaguement apparentés, la théorie du gnomon est une véritable théorie mathématique, régie par une loi cadre : la loi du gnomon.

Rappelons que le cône, ou son antagoniste logique : l'entonnoir, affecté d'un tenseur binaire de contraction-expansion, (et entouré d'une sphère), était déjà la structure qui se dégageait avec le plus de vraisemblance du système cosmologique d'Empédocle⁽¹⁾; et la simple forme matérielle du lambda de Platon indique que cette structure est aussi à la "racine" de l'univers du Timée, racine qui est à la fois logique (gnomonique) et musicologique. A la lumière de ces précieux enseignements pythagoriciens, ce légume d'une invraisemblable beauté mathématique, qui nous offre une représentation de l'union parfaite de la monade et de la dyade indéterminée, de la tension ternaire fermante et de la tension binaire ouvrante, et qui n'a sans doute pas fini de livrer ses secrets, mériterait, à coup sûr, d'être étudié avec plus de considération qu'il a pu l'être jusqu'ici.

 

Tous les cônes sont affectés d'une torsion caractéristique, la torsion en "spirales d'or"; en revanche, la distribution géométrique des points de la sphère (circonscrite au cône principal) vers lesquels tendent leurs innombrables sommets, semble, à première vue, générée par un processus  libre ou "aléatoire", un peu comme si chacun des milliers de sommets monadologiques bourgeonnant à la surface du chou (et ce à toutes les échelles de celui-ci) constituait une entité individuelle, dotée d'un mouvement autonome.

 

(05.01.2015)

 

 

⁽¹⁾ Empédocle emploie l'expression : "reflux vers les bords du cercle" pour caractériser le mouvement de l'Un vers le Multiple. La limite d'expansion du Multiple est donc bien un cercle. Dès lors, si l'on veut bien nous concéder que l'univers d'Empédocle n'est pas plat, il est nécessairement conique.

 

 

 

 

 

Références :

Joscelyn Godwin : The harmony of the spheres, a sourcebook of the Pythagorean Tradition in Music

Leon Crickmore : A possible Mesopotamian origin for Plato's World Soul,

A Re-valuation of the ancient science of harmonics

 

  

 

 

 

..........................................................................................................................

 

 

 NOTICE HISTORICO-CRITIQUE :

 

L'ORIGINE DU TIMEE

 

 

Platon plagiaire?

Nous n'avons ni le loisir, ni les moyens de nous intéresser longuement à cette question historique, dans sa dimension potentielle d'enquête policière. Il nous semble que la querelle du Timée repose, à travers les âges, sur un fondement assez simple, qui est le sentiment que Platon n'a jamais fait montre, ni avant, ni après, du génie proprement scientifique qui éclate en quelques passages du Timée.

Les premières accusations précises de plagiat furent lancées, quelques décennies après sa mort, par le talentueux satiriste Timon de Phlionte, cité par Aulu-Gelle :

"Et toi aussi, Platon, le désir du savoir t'a saisi.

A prix d'or, tu t'es approprié

Un mince ouvrage dont tu as pris le meilleur,

Et qui t'a enseigné la timéographie."*

Elles furent ensuite relayées par divers auteurs anciens, tels qu'Hermippe de Smyrne, Satyros, Diogène Laërce, Jamblique, ou Proclus, qui attribuent l'ouvrage, les uns à Timée, les autres à Philolaos, mais aussi modernes, - jusqu'à nos jours. Plutôt discrets jusqu'au XXe siècle, les défenseurs de Platon n'ont, depuis, pas manqué de ressources, puisque l'un d'eux est même parvenu à la conclusion que plusieurs auteurs pythagoriciens de premier plan, comme Philolaos et Timée, n'avaient jamais existé, mais n'étaient que des personnages de comédie inventés par Platon. En raison de la circularité de son principe, il n'est pas rare que la méthode hypercritique, fondée sur la sempiternelle constatation que "nous ne savons rien, ou presque, de ce dont nous sommes professionnellement investis de vous entretenir quand même", accouche assez facilement de l'objet de sa pire hantise, à savoir des élucubrations les plus gratuites. Sans entrer dans le détail de cette controverse qui n'a, en elle-même, d'intérêt que pour les amoureux de Platon, - ou éventuellement pour ceux qui pourraient être aujourd'hui encore tributaires de ce supposé plagiat, en vertu du "déterminisme" inhérent à leur carrière universitaire, comme les rédacteurs de thèses sur le Timée, - on peut se contenter de remarquer qu'un "paquet" assez consistant de concepts pythagoriciens, d'un caractère nettement technique, tels que : paradigme, réceptacle, médiétés, âme du monde, harmonie, solides réguliers, symétrie hexagonale (triangle équilatéral), même, autre, mélange, etc, toutes notions qui sont organiquement subordonnées à la construction pythagoricienne, ou gnomonique, de la gamme musicale, objet de cet article, et que l'on trouve attestées ou corroborées par ailleurs, soit par des témoins solides de la tradition, soit par des éléments constants de la doctrine : - toutes ces notions caractéristiquement pythagoriciennes, donc, font avec le Timée leur apparition groupée dans l’œuvre de Platon, à une époque où celui-ci doit avoir entre soixante-cinq et soixante-dix ans, où il ne lui reste qu'un ou deux dialogues à écrire, et quelques années seulement après la rédaction du Phédon, dans lequel il avait entrepris de démontrer, au prix d'une certaine incohérence doctrinale, que la conception pythagoricienne de l'âme comme "harmonie" - qui est le postulat de base du Timée - était logiquement inconsistante, et qu'on devait lui préférer de beaucoup la conception de la connaissance comme réminiscence, (pourtant elle-même empruntée par Platon, selon toute vraisemblance, à la doctrine ésotérique orphico-pythagoricienne, bien qu'elle soit évidemment plus ancienne et à vrai dire sans âge, puisqu'elle appartient au registre des vérités métaphysiques éternelles, auquel s'abreuve tout enseignement traditionnel).

On en conclura assez raisonnablement, peut-être, que la documentation de Platon en matière de théories scientifiques pythagoriciennes demeura, - jusqu'au Timée, -  très en retard sur ce que pouvaient être, par exemple, ses connaissances en matière de pythagorisme ésotérique, ce qui peut s'expliquer par deux raisons principales.

D'une part, la "religion" orphico-pythagoricienne, même si elle relevait du secret initiatique, ne constituait pas un domaine réservé des pythagoriciens, puisque l'orphisme avait d'autres racines sur le sol grec, auprès desquelles on sait aujourd'hui que Socrate et Platon avaient pu recueillir diverses traditions orales; - tandis que tout ce que l'on sait du secret  "sectaire"  et scolaire proprement pythagoricien, est qu'il concernait, en premier lieu, le savoir scientifique : les théorèmes et les démonstrations. Certes, des contacts avaient existé entre l'école de Socrate et celle du pythagoricien Théodore de Cyrène, alors à la pointe du mouvement mathématique; mais, si l'on en juge par le Théétète, qui ne témoigne pas d'une compréhension bien profonde des questions soulevées par la spirale de Théodore, ces contacts ne semblent pas avoir été aussi étroits qu'on le suppose d'habitude. Quant à prétendre, comme certains n'hésitent pas à le faire, que Théodore fut le "professeur de mathématiques de Socrate, Théétète et Platon", cela nous paraît pour le moins abusif, car, si l'on s'en tient au récit de Platon, Théétète, informateur de Socrate, ne semble pas connaître la raison - pourtant très simple - pour laquelle la monstration de Théodore s'était arrêtée au nombre 17.

Mais d'autre part cette relative négligence des questions scientifiques peut s'expliquer par la personnalité même de Platon, auteur qui fut dominé tout au long de sa carrière par des préoccupations d'ordre principalement esthético-moral. Les idées du Bien et du Beau sont en effet les seuls apports réellement originaux de Platon au patrimoine de la réflexion philosophique; et il faut convenir que ces préoccupations ont absorbé l'essentiel de l'effort qu'on a désigné, après lui, par le mot philosophie, avant qu'il ne s'épuise. Car, de fait, à bien y regarder, ce qu'on désigne couramment sous ce nom ne recouvre, la plupart du temps, qu'une certaine esthétique associée à une certaine morale, ou le contraire. Toute proportion gardée, la présence du Timée dans l'oeuvre de Platon peut donc apparaître aussi incongrue que le seraient, par exemple, un article de Gödel ou de Majorana (en l'occurrence : les deux à la fois) introduits par mégarde dans l’œuvre de Nietzsche ou de Bergson; - pour citer, peut-être, les deux derniers penseurs occidentaux à avoir arboré le statut de philosophe avec un semblant de crédibilité, le costume n'étant, manifestement, déjà plus adapté aux spécificités de l'"intellectuel" du XXe siècle, assigné à des tâches plus spéciales. "C'est seulement comme phénomène esthétique que l'existence et le monde sont éternellement justifiés" (La naissance de la tragédie). Avec la franchise qui le caractérise, Nietzsche admet son incapacité pure et simple à concevoir une forme de compréhension plus élevée, de même que Bergson ne pouvait concevoir la réalité autrement que comme une sorte d'"artiste" (L'Evolution créatrice). Et si l'on veut revenir à l'origine de ce mouvement intellectuel, qui prend sa source, comme on l'a dit, dans la philosophie éthique et esthétique de Platon, il faut être bien conscient que, du point de vue de la connaissance métaphysique, qui est celui où s'enracine la doctrine de Pythagore, les problèmes de cette nature, les problèmes éthiques et esthétiques sont, non seulement dépourvus d'intérêt, mais en un sens plus profond, qui demanderait certes à être explicité, ils sont dépourvus même d'existence.

On pourrait nous objecter que d'autres auteurs, comme Kant, ne se sont "révélés" philosophiquement qu'à un âge assez avancé; mais l'argument ne change rien à la possibilité que, pour Platon, cette tardive "révélation" se soit produite à la lecture d'un traité de physique pythagoricienne, qu'il soit l'oeuvre de Timée ou d'un autre. Ajoutons que la construction de ce dialogue, maladroite et contournée, donne l'impression qu'une théorie scientifique de l'univers s'y trouve introduite un peu par hasard, comme une pièce rapportée; - pièce que l'auteur s'est contenté de faire précéder d'un échantillon sans surprise de son catéchisme personnel, selon lequel "Dieu, étant Bon, n'a pu créer le monde que Beau", sans égard pour le fait que la doctrine du Timée relève d'un postulat scientifique, d'un raisonnement hypothético-déductif, où le monde n'est supposé avoir été créé de telle manière, que parce que telle est la manière dont nous pourrions, ici et maintenant, le recréer nous-mêmes : point de vue qui est intellectuellement contradictoire avec ce type d'approche esthético-morale, lequel ne relève en soi que d'une forme assez inférieure de pensée religieuse.

Pour une documentation plus fournie, on pourra s'en remettre à Luc Brisson, auquel a été dévolue, pour la période récente, la mission de défendre les prérogatives supposées de l'auteur Platon, (statut que le principal intéressé, précisons-le, ne semble pas revendiquer explicitement lui-même, en plaçant son récit sous l'autorité d'un pythagoricien italien, plutôt que sous le patronage de "Socrate", qui lui sert habituellement de pseudonyme), et qui a consacré à la question plusieurs articles dûment garnis de références. On pourra remarquer en les lisant que la méthode hypercritique a certains traits de ressemblance avec celle des révisionnistes : rien n'est prouvé, donc rien n'a jamais existé. Ainsi, pour Brisson, il n'est pas prouvé qu'Archytas ait été pythagoricien, et il n'est pas prouvé que le passage du Phédon sur la conception pythagoricienne de l'âme comme harmonie, concerne réellement la conception pythagoricienne de l'âme comme harmonie. A ce régime, nous pourrions aussi nous demander s'il est prouvé que la phrase que nous écrivons en ce moment soit bien réelle.

L'affaire du plagiat de Platon inspire à Brisson une réflexion épistémologique de haut vol sur "la manière dont travaillaient les historiens de la philosophie dans l'antiquité", qui nous donne l'occasion de nous extasier sur la merveilleuse différence qui existe entre leurs méthodes de quasi-primitifs et "nos méthodes scientifiques actuelles". Le ton est donné : nous n'allons pas spécialement prendre connaissance des idées de M. Brisson, mais avant tout bénéficier de l'immense avantage que nous procure la lumière du savoir universitaire moderne, avec ses techniques reconnues et éprouvées. Pour Brisson, en effet, tous les témoignages de l'antiquité sont sujets à caution, et donc, à l'état brut, inutilisables, du fait que leurs auteurs étaient, malheureusement, ignorants de la véritable science historique. Avant même d'être examinés individuellement, ces témoignages doivent donc être regroupés dans un tableau analytique et classés par catégories, en fonction du genre d'aliénation ou de préjugés culturels dont pouvait être affecté leur auteur. Cette méthode, qui pourrait à première vue apparaître un peu simple, s'avère à l'usage d'une efficacité indiscutable. Habitué à se mouvoir à son aise sur les cimes de la philosophie grecque, le professeur Brisson, grâce à son tableau bien conçu, est ainsi parvenu à épingler en un clin d'oeil une bonne douzaine de ces prétendues "autorités anciennes", et à en démasquer la moitié comme de pathétiques affabulateurs, et l'autre moitié comme d'innocents perroquets, conditionnés à répéter ces contes de bonnes femmes. L'autre avantage de cette méthode étant qu'elle nous dispense, en tout état de cause, d'examiner de plus près ces infortunés auteurs et leurs ennuyeux ouvrages, comme elle nous dispense d'essayer de comprendre, par exemple, pourquoi plusieurs d'entre eux ont la manie de se déclarer "pythagoriciens", ou celle, encore plus loufoque, de considérer Platon comme un disciple de Pythagore.

Car en ce domaine, il est bien connu que rien n'est prouvé, et donc, rien n'a jamais existé : ni Timée, ni Archytas, ni Philolaos....ni, davantage, la conception pythagoricienne de l'âme comme harmonie.

Si ces remarques peuvent apparaître sans indulgence, elles ne sauraient occulter le fait qu'une partie importante de l'exégèse "vingtième-siécliste" de l'antiquité philosophique aura été dominée par le préjugé, aussi niais que désastreux, mais encore dominant à notre époque, selon lequel les anciens nous auraient été, à quelque égard que ce puisse être, intellectuellement inférieurs. Dans cette situation, il faut voir une conséquence du règne moderne de l'idéologie scientiste, avec son concept vulgaire du progrès et son culte idolâtre de la fausse "expertise", à laquelle correspond, dans son registre, une fausse exégèse, discours fondé sur une croyance en la magie des méthodes, qui, quoi qu'il veuille saisir, ne rencontre jamais que soi-même, et qu'il importe de bien distinguer de la véritable exégèse qui, elle, consiste toujours au contraire à accueillir les textes anciens dans leur signification naïve et intemporelle, en tant que ce qu'ils avaient à transmettre était important et simple, et peut nous être restitué ici et maintenant, et qui exige donc une sympathie, une intelligence et une implication personnelle du commentateur, bien éloignée d'un quelconque dogmatisme professionnel, jaloux de ses précieuses "méthodes" et, de ce fait même, cuirassé par un "recul historique", une "distance critique" dont on se passerait volontiers, vu leur caractère oppressant de taupinière intellectuelle.

*

Seul Platon, bien entendu, survit à l'épreuve de cette lessive historico-philosophique, révélatrice avant tout d'une compréhension très insuffisante des réalités mathématiques essentielles qui sont à la base du Timée, et qui font de ce traité ce qu'il est en réalité : l'aboutissement d'un immense effort scientifique interdisciplinaire, - musicologique, cosmologique, logique, mais aussi, par induction générale, relatif à la physique fondamentale, - effort commencé avec Pythagore, et poursuivi, par une tradition directe et ininterrompue, pendant cinq à six générations. Dans ce mouvement, le rôle de Platon, non négligeable, aura été de nous transmettre un dossier scientifique, malheureusement incomplet, dont l'origine italienne, à nos yeux comme à ceux de beaucoup d'autres, anciens comme modernes, n'a jamais fait l'objet d'insupportables doutes.

 

 

Platon et Archytas : la rencontre du sophisme et du pythagorisme

Les voyages en Italie de Platon, ses contacts - empreints d'une évidente méfiance mutuelle - avec Archytas et les derniers pythagoriciens italiens qui furent ses contemporains, et selon plusieurs l'achat (bien excusable, car, à sa place, nous aurions fait la même chose), de quelques livres pythagoriciens, lui auront donc, selon toute apparence, permis de combler tardivement ses lacunes en matière de science.

Concernant ses rapports avec les pythagoriciens : même si Archytas a sauvé Platon du péril de mort où l'avait entraîné sa petite politique de "courtisan-philosophe" auprès de la famille des tyrans de Syracuse, (entreprise de longue haleine, puisqu'il a successivement et vainement tenté sa chance auprès des deux Denys, père et fils), on imagine la méfiance, sinon la condescendance que ce pythagoricien pouvait ressentir pour la nouvelle conception de la politique incarnée par Platon, associant la courtisanerie servile à une prétention "théorique" personnelle totalement utopiste - modèle d'"action" qui sera ensuite imité par Aristote auprès de Philippe de Macédoine, (avec plus de réussite, puisqu'au prix d'une renonciation complète à son "idéal théorique"), et qui est le style politique caractéristique de l'idéologie sophiste, mouvement intellectuel athénien auquel Socrate, Platon, et Aristote n'ont jamais cessé d'appartenir; en dépit du déni un peu naïf de la tradition philosophique occidentale à ce sujet 

Aux antipodes de cette conception avant-gardiste de l'intellectuel comme "soliste libéral", Archytas, lui, comme la plupart des pythagoriciens des générations précédentes, était engagé dans une action politique de haut vol, et exerçait les plus hautes fonctions administratives, puisqu'il fut élu à sept reprises stratège de sa ville de Tarente avec les fonctions de roi. - Rappelons que les disciples directs de Pythagore ont régné pendant plusieurs décennies sur une bonne partie de la "Grande Grèce", région du sud de l'Italie dynamisée par un peuplement grec récent, et qui représentait alors pour le vieux monde grec un "nouveau monde", une terre d'aventure et de liberté propice aux expérimentations politiques. Les pythagoriciens contrôlèrent ainsi les puissantes cités de Crotone, Locres, Tarente, Métaponte et beaucoup d'autres, avant un soulèvement généralisé qui les chassa presque partout du pouvoir, hormis dans quelques poches résiduelles, telles que la cité de Tarente justement, à laquelle Platon dut sa survie.

 

Particularité du mouvement sophiste

Les dialogues de Platon relatent complaisamment la manière dont Socrate se livrait, avec les autres principaux "éducateurs" sophistes de son temps, à un véritable trafic de disciples, habituellement sélectionnés selon des critères explicites : de jeunes garçons beaux et riches, - des aristocrates tels que Charmide, Alcibiade ou Platon lui-même ayant été, notoirement, "distingués" selon ces critères. Il y avait là, assurément, un marché loin d'être négligeable, puisque les sophistes étaient réputés percevoir des salaires énormes : jusqu'à 100 mines pour des vedettes comme Protagoras ou Gorgias, soit cent fois le salaire d'un artisan. Ainsi, pour J-L. Périllié, les propos que Socrate tient à Théétète : "Il y en a beaucoup que j'ai donné en cadeau à Prodicos..." se réfèrent à "toute une pratique de mise en circulation des jeunes gens, pour ne pas dire des éphèbes, au sein d'un réseau sophiste." Le prestige de Socrate tenait en partie à une compétition objective existant entre les sophistes, sur le fait de savoir lequel d'entre eux s'était "attaché" les adolescents les plus mignons et les plus riches; car, en dépit de sa laideur légendaire et de ses origines pouilleuses, son tableau de chasse était sans égal. Vue la simplicité avec laquelle Platon en fait état, il n'y a aucune raison de penser que les choses aient changé à son époque, pas plus qu'à celle d'Aristote. Il n'est certainement pas abusif de parler du caractère vénérien - au sens étymologique - de la transmission du savoir en milieu sophiste. Ce sont là des réalités culturelles, propres à ce mouvement athénien, considéré aujourd'hui comme le berceau de la philosophie académique, qui, même si elles sont bien connues, méritent d'être rappelées de temps à autre; d'autant qu'elles offrent un contraste net avec la tradition pythagoricienne, réputée, d'une part, pour son "féminisme" quelque peu bizarre, d'autre part, pour les critères rigoureux selon lesquels étaient orientés et formés les étudiants, en fonction de leurs capacités purement intellectuelles, notamment mathématiques. Ces deux traditions s'avèrent donc antagonistes, même si elles peuvent avoir ça et là des racines communes. Dans la première, la transmission de la connaissance demeure attachée à certains modèles archaïques d'initiation rituelle, d'un type que l'on peut qualifier d'érotico-religieux. Dans l'autre - novatrice sur ce point - la nature purement intellectuelle du savoir scientifique est clairement revendiquée; et c'est donc la science elle-même, avec ses difficultés, qui est seule juge de l'aptitude de quiconque à devenir l'un de ses desservants. Enfin, dans la première, le développement des "écoles" de pensée se réalise sous la forme de petites entreprises professionnelles et commerciales, tandis que, dans la seconde, le développement des systèmes et des innovations personnelles s'accomplit à l'intérieur d'un même monde, qu'on pourrait appeler le monde pythagoricien, au sein duquel les individualités n'ont pas d'importance. Et de fait, aujourd'hui encore, la science pythagoricienne ne peut se comprendre autrement que comme un continuum, au sens mathématique du terme; (ce qui implique aussi, à travers les âges, une amitié et une fidélité, une association de confiances qui ont conduit à définir la nature de Pythagore comme "quelque chose d'intermédiaire entre Dieu et l'Homme") - Quant aux rapports commerciaux et vénaux, la fraternité pythagoricienne s'en était préservée dès l'origine, comme on sait, par une organisation sectaire favorisant un communisme spontané, de type familial. Ces remarques peuvent apparaître un peu simplificatrices; mais elles n'ont pas d'objet plus ambitieux que de pointer quelque uns des aspects par lesquels ces deux cultures sont hétérogènes.

Dans le foisonnement des doctrines issues de la "révolution" sophiste, seul le mouvement cynique représente un foyer de résistance et d'attachement aux formes de la sagesse traditionnelle, notamment par la sublimité de sa doctrine morale, insurpassée à ce jour - morale essentiellement pratique, monstrative, gestuelle, visant à démolir de façon systématique les constructions "idéologiques" de la sophistique, et dans laquelle on peut certainement retrouver l'image de la véritable morale pythagoricienne, aux antipodes de la bouillie insipide que les néo-platoniciens ont prétendu reconstituer, et nous vendre pour telle.

 

La fin de Platon

La véritable histoire intellectuelle de Platon est tout autre que celle qu'on nous raconte. Platon fut, au soir de sa vie, littéralement écrasé par l'ombre de Pythagore, qu'il ne mentionne qu'une seule fois dans toute son oeuvre, et dont il a pu éprouver la prodigieuse fécondité intellectuelle au nombre des disciples qu'il avait conservé de son vivant, jusque dans son entourage le plus proche. De fait, à la mort de Platon, l'académie a fait l'objet d'un véritable "putsch" ou d'une "restauration" pythagoricienne. Le premier acte de Speusippe comme chef de l'académie a été d'envoyer aux oubliettes la doctrine platonicienne des idées, pour réaffirmer que les idées ne sont absolument rien d'autre que les nombres; et ramener tout le monde à l'étude de la décade et de la tétractys. Son successeur à la tête de l'académie, Xénocrate, sera lui aussi un pythagoricien pur sucre, sans héritier il est vrai; puisque l'école effectuera après eux un retour définitif au platonisme; mais c'est sous le règne de ces deux premiers scholarques qu'a été publié l'Epinomis, qui n'est pas seulement un manifeste pythagoricien, mais aussi, de façon assez évidente, un manifeste "anti-platonicien", ouvrage que personne ne songe plus aujourd'hui à attribuer à Platon, mais sur lequel son nom a été apposé par ses propres disciples sans le moindre scrupule... après tout, n'avait-il pas lui-même montré l'exemple avec le Timée? - Plus étonnant encore, on sait moins que l'école d'Aristote a, elle aussi, après la mort du maître, dû faire face à une tentative de subversion ou de putsch pythagoricien, qui n'a dû qu'à des circonstances aléatoires de ne pas connaître le même succès que la précédente, au prix d'une scission ou en tous cas dune "purge" au sein de la troupe des disciples d'Aristote. Et l'on peut aussi se rappeler que la secte pythagoricienne était déjà bien représentée dans la cellule de condamné de Socrate, dans le groupe des derniers amis à lui rendre visite, et prête à organiser sa fuite et son exil, à l'heure où le téméraire Platon soignait son rhume.

 

La doctrine des idées

D'un point de vue pythagoricien, la doctrine platonicienne des idées ne peut apparaître, aujourd'hui comme hier, que comme une construction inutile et confuse, destinée avant tout à recycler la doctrine du nombre à la moulinette de la "moraline" et de l'"esthétine", avec comme conséquence historique fatale, l'abandon de la philosophie naturelle inhérente à la véritable doctrine du nombre, - philosophie qui est, quant à elle, aussi éloignée que possible de quelque idéalisme que ce soit.

 

L'héritage de Platon

Platon n'a pas eu de disciple, en ce sens que ceux qui l'ont côtoyé physiquement, ceux qui l'ont vu vivre, ne se sont affirmés individuellement que par différentes formes de rejet de la pensée platonicienne. Platon n'a donc produit que des émules, des imitateurs, au premier rang desquels Aristote.

En revanche, notre système éducatif actuel, qualifié avec justesse par Jean-Claude Michéa de système d'enseignement de l'ignorance, et héritier d'une longue tradition académique, peut certainement être considéré comme une tentative sérieuse de réaliser l'utopie platonicienne de la République : celle d'une société parfaite cimentée par des mensonges institutionnels.

"C’est donc à ceux qui gouvernent la cité – si vraiment on doit l’accorder à certains – que revient la possibilité de mentir." (La République)

Pour le philosophe Cédric Enjalbert, la réflexion sur le mensonge participe chez Platon à l’établissement de la justice dans la cité idéale. Il est utile aux hommes à la manière d’une espèce de drogue, car il possède les mêmes effets : accoutumance, stimulation et anesthésie, tous propices à tenir les hommes à leur place, comme des animaux dominés, dressés.

Or tels semblent bien être, selon l'évidence, les principes qui ont inspiré depuis quelques décennies l'évolution de nos systèmes d'éducation.

Stratégie que Jean-Claude Michéa résume dans cette formule, parodiant une maxime de Planck sur la vérité scientifique et ses adversaires :

"Le mensonge ne triomphe jamais entièrement par lui-même, mais ses adversaires finiront bien par mourir."

 

 

*La cité de Phlionte fut, avec celle de Thèbes, où l'exilé Philolaos avait reformé une "école" sur ses vieux jours, l'un des centres pythagoriciens les plus importants parmi ceux qui étaient actifs du vivant de Socrate et du jeune Platon. On peut donc tenir pour vraisemblable que Timon ait pu recueillir, dans cette cité marquée par l'influence des pythagoriciens, un certain nombre de documents ou de traditions locales, concernant une affaire de plagiat qui, selon les datations courantes, se serait produite environ trente-cinq ans avant sa naissance.

 

 

 

Référence :

Luc Brisson : Les accusations de plagiat lancées contre Platon.

La particularité de ce texte est qu'il s'efforce de répondre à un problème historique bien précis : l'origine du Timée, tout en s'appliquant, dans le même temps, à en nier l'existence, ce qui implique que ledit problème puisse être "dissous" dans un flot de "rumeurs" du même acabit, toutes également dépourvues de fondement. Le texte obéit ainsi à une "double contrainte" dont il n'est, en soi, pas inintéressant de suivre le développement.

 

 

 

 

 

 

 

Vesica Piscis

 

 

 

 

 

 

par G. Denom

 

 

 

 

 

 

 

 

Le vesica piscis, appelé aussi mandorle (amande), est la figure géométrique formée par l'intersection de deux cercles de même diamètre, lorsque le centre de chacun appartient à la circonférence de l'autre.

 

 

Malgré le succès de cette figure dans la mouvance new-age, comparable à celui du nombre d'or, qui permet à certains d'élucubrer à son sujet plus que de raison, Axel Schneider a raison d'insister sur le fait qu'elle est au coeur d'un ensemble de spéculations ésotériques assez anciennes, ensemble qui, en raison notamment de sa nature mathématique, peut - une fois n'est pas coutume - être reconnu comme authentiquement pythagoricien.
Quelques illustrations suffiront, en effet, pour montrer que cette structure mathématique, d'un haut degré de généralité, permet de retrouver la plupart des thèmes de la mathématique pythagoricienne. 

Mieux, nous pensons même que le vesica piscis est l'une des clés majeures de l'ésotérisme pythagoricien, par la richesse des connexions qu'il établit entre les différents concepts de cette doctrine.

Le vesica piscis est "construit" par l'entrecroisement de deux cercles. Il est évidemment tentant de voir dans cette figure une représentation mathématique de la dialectique pythagoricienne de la nature : le Même, l'Autre, et le Mélange. Le vesica piscis évoque aussi la représentation symbolique la plus courante de la notion d'ensemble; où la région du Mélange correspond alors à l'intersection de deux ensembles. Sur cette base logique, le vesica piscis peut être envisagé comme un processus topologique d'ouverture progressive, à partir d'une situation où les deux ensembles seraient disjoints, ou simplement tangents, et leur intersection nulle, ou égale à un seul point - processus d'ouverture qui serait stoppé par un effet "magnétique" à l'instant précis où le centre de chaque cercle rencontre la circonférence de l'autre.

Cette structure se signale par le contraste entre la simplicité des moyens de construction, et la richesse des contenus mathématiques associés. En elle-même, elle semble comporter un principe de générativité, qui l'apparente à la tétractys. Les deux structures se déduisent d'ailleurs l'une de l'autre en ce que, si l'on coupe le vesica piscis par une ligne médiane, les quatre points d'intersection coïncident avec le quatrième étage de la tétractys, autrement dit avec le degré d'extension ou d'"ouverture" maximale de cette structure. Sous ce rapport, la tétractys peut donc apparaître comme le critérium en fonction duquel s'ajuste l'ouverture propre du vesica piscis.                

                                     

 

Une conception assez répandue associe le vesica piscis au yoni qui désigne, en sanskrit, l'organe génital féminin. Cette conception, quelle qu'en soit l'origine, apparaît totalement justifiée, si l'on prend soin de préciser que, dans la métaphysique indienne, le yoni est avant tout un symbole qui se rapporte au principe ou au "pôle" féminin de la manifestation universelle, correspondant à ce titre au linga (phallus). Or selon la loi du symbolisme, toujours difficile à intégrer pour nos mentalités modernes, (à moins que l'on soit passé entre les mains de pédagogues comme Guénon ou Borella), c'est toujours l'inférieur qui symbolise le supérieur. Ce sont donc les réalités naturelles qui sont, dans leur ordre propre, des symboles des principes métaphysiques qui leur préexistent; puisqu'elles n'en sont qu'une expression déterminée et contingente; et c'est le "yoni", organe génital féminin, qui symbolise selon son mode le yoni, attribut du pôle féminin de la manifestation cosmique, dont il n'est qu'une expression déterminée dans l'ordre naturel, comme le symbole mathématique du vesica piscis peut l'être dans l'ordre intellectuel qui est le sien.

Mais il est plus intéressant de remarquer que, dans la tradition hindoue, le yoni est constamment associé à l'image du filet de pêche. En maint endroit de la littérature sanskrite, il est dit que le principe divin de la création étend ses "yonis" (toujours alors conçus comme une réalité plurielle) comme le pêcheur étend ses filets. Et la même image se retrouve, à peu de choses près, chez Empédocle. L'ensemble de ce symbolisme tourne donc bien autour de la nature; la génitalité sexuelle n'étant ici qu'un cas particulier. La nature cosmique tout entière procède de la même manière pour créer à tous ses étages : en étendant ses filets, ses yonis qui sont, si l'on veut, des "vessies", des sacs, ou des alvéoles, au sein desquels naissent ou se forment des "poissons", - des monades.

 *

"Simon-Pierre monta dans la barque, et tira à terre le filet qui était plein de cent cinquante-trois grands poissons; et quoiqu'il y en eût un si grand nombre, le filet ne se rompit point." Jean, 21, 11.

Il est assez vraisemblable que la recherche historique sur ce symbole ancien, et sur la doctrine ésotérique qui lui est associée, ait pu être entravée par le fait qu'elle conduirait à "démasquer" un peu trop de pythagoriciens parmi les auteurs du Nouveau Testament, dont Saint Jean et Saint Paul... - si le soupçon ne s'étend pas jusqu'au Christ lui-même, comme le suppute Schneider. Mais ceci ne ferait que corroborer les géniales intuitions de Simone Weil, qui intègre Saint Jean dans sa liste des sources pythagoriciennes les plus décisives de l'antiquité.

 

  

 

 

Quelques propriétés géométriques et arithmétiques remarquables

 

 

 

 Le Vesica piscis et le triangle équilatéral,

 dont la hauteur est égale à 1/2 de racine de 3

 

 

 

 Vesica piscis et triangle gnomonique de rang 2

 

 

 

 Vesica piscis et racines de 1, 2, 3 et 5,

 qui donnent les hypoténuses de 4 des 5 premiers triangles de Théodore

 

 

 

La mesure du Poisson selon Archimède, avec, pour paradigme, le "filet" : le polygone gnomonique de rang 4 (losange de 60/120 degrés) qui est géométriquement issu de la transformation du triangle gnomonique de rang 4 en carré gnomonique de rang 4, ou qui correspond, plutôt, à la phase intermédiaire de ce processus, comme on l'a vu sur le blog 1 (gnomon d'un polygone régulier). Dans le cadre du symbolisme évoqué plus haut, il est intéressant de remarquer que le "lancer de filet" de la création universelle correspond au développement quaternaire, sous la forme d'une transformation géométrique, de la loi du gnomon : "le gnomon du triangle équilatéral est égal au gnomon du carré"; - transformation représentée ici par son moment intermédiaire, transitionnel.

 

   

 

En effet, le triangle gnomonique se transforme en carré gnomonique, par une rotation de 180 degrés des cellules monadiques qui sont ses triangles "pointe en bas", suivie d'une modification de 30 degrés du paramètre angulaire (passage du rapport 120/60 au rapport 90/90). Dans cette logique, les blocs atomiques composant les objets gnomoniques sont considérés comme des cellules "souples", ou "plastiques", génératrices de polygones minimum, polygones qui se "solidifient" en fonction de la configuration angulaire des "noyaux" qui sont leurs centres géométriques de référence, - un peu à la manière dont les choses se passent pour les alvéoles des abeilles.

 

 

 

La construction, par Dürer, du pentagone adjacent à l'hexagone, "à la manière dont, d'après la tradition, le créateur a conçu le plan de l'univers : avec une ouverture de compas inchangée", - c'est à dire selon le principe de symétrie, ou de commensurabilité. Pour Dürer aussi, le vesica piscis est donc associé au thème de la création du monde. Dans cette construction, les deux polygones, pentagone et hexagone, sont définis au moyen de trapèzes spécifiques, correspondant aux quatre points d'intersection de chacun de ces polygones avec les deux cercles générateurs du vesica piscis.

 

 

 

Cette remarquable construction, due à Yvo Jacquier, illustre la correspondance entre le vesica piscis, le pentagramme, et les premières étapes de la division du triangle d'or de Penrose. Ici, c'est  l'"amande" intérieure du vesica piscis qui détermine les coordonnées du trapèze du pentagone.

 

 

le 23.09.2014

 

 

 

 

Glose :

On peut remarquer que le nombre 153, somme des 17 premiers entiers et des 5 premières factorielles, et connu par diverses propriétés remarquables, est aussi le troisième des nombres engendrés par l'addition, en ordre croissant, des cubes gnomoniques impairs, série dont le quatrième membre est le nombre parfait 496, évoqué ailleurs sur ce blog, et dont les deux premiers sont les nombres 1 et 28.

1³=1

1³+3³=28

1³+3³+5³=153

1³+3³+5³+7³=496

 

Soit :

  +     +      = 153

 

                                           +   = 496

 

En empilant ces cubes les uns sur les autres, la progression de ces nombres peut être représentée par un gratte-ciel dont la base s'élargit, de tous les côtés, d'un cube à chaque étape.

Tous les nombres de cette famille sont non seulement triangulaires, - c'est-à-dire qu'ils peuvent s'exprimer comme des sommes d'entiers successifs à partir de 1, les 4 premiers étant respectivement les sommes des : 1, 7, 17 et 31 premiers entiers... d'où : ces nombres ordinaux étant séparés par les intervalles : +6, +10, +14, ..., on déduit aisément que le prochain membre de la série, le nombre 1225, sera égal à la somme des 49 premiers entiers, puisque 31+18=49, - mais en outre hexagonaux; les nombres hexagonaux n'étant du reste que les nombres triangulaires de rang impair.

 

 

 

 

RECTANGLE DE FIBONACCI

ET

TRIANGLE D'OR DE PENROSE

  

 deux applications géométriques de la médiété Nicomaque 10

 

  

 

par Guillaume DENOM 

  

 

Pourquoi les ouvrages de la nature
sont-ils si parfaits ? C'est que chaque ouvrage
est un tout, et qu'elle travaille sur
un plan éternel , dont elle ne s'écarte
jamais; elle prépare en silence les germes
de ses productions; elle ébauche par un
acte unique la forme primitive de tout
être vivant ; elle la développe , elle la
perfectionne par un mouvement continu,
et dans un temps prescrit. L'ouvrage
étonne, mais c'est l'empreinte divine dont
il porte les traits qui doit nous frapper.

Buffon

discours de réception à l'Académie Française

 

 

 

 

 

Bien que plusieurs auteurs aient déjà signalé que la « suite de Fibonacci » était une notion connue et définie depuis l’antiquité dans le cadre du système des médiétés, la littérature mathématique contemporaine continue d’utiliser l’expression « suite de Fibonacci », au mépris de la réalité historique, pour désigner cette notion. La plus ancienne trace écrite de cette notion figure dans  l’Introduction arithmétique de Nicomaque de Gérase, soit plus d’un millénaire avant Fibonacci; en outre, Nicomaque nous précise qu’il n’en est pas lui-même le découvreur, sans indiquer à quelle source il l’a puisée.

Si cette occultation historique est fâcheuse, ce n’est pas pour des raisons de « propriété intellectuelle » qui n’ont, en pythagorisme, aucune espèce d'importance, mais pour la compréhension même de la notion dont il s’agit.

En effet, il n’existe pas de définition plus synthétique, ni plus profonde, de la suite de Fibonacci, que celle qui est donnée dans le cadre du système des médiétés, où elle ne constitue qu’un cas particulier, ou, si l’on préfère,  un élément, d’un ensemble qui en compte 12.

Avant d’aller plus loin, rappelons que, dans le système des médiétés,  trois nombres : a, b, c, sont en proportion « de Fibonacci » (c'est-à-dire en « médiété Nicomaque 10 ») si et seulement si ils satisfont entre eux la relation :

(c - b) = a

(c - a)    b

 

*

  

Dans son Dossier Pythagore, Pierre Brémaud signale une propriété très intéressante des nombres de Fibonacci.

 

« Terminons cette liste des propriétés remarquables de la suite de Fibonacci par celle-ci :

              

« La figure suivante devrait convaincre le lecteur de la justesse de cette relation et de la beauté de l’arithmétique géométrique modo pythagorico. »

  

         

     

Pierre Brémaud, Le dossier Pythagore, p 290.

 

La construction de M. Brémaud est en effet des plus intéressantes, puisqu'elle revient à définir une relation constante entre la suite des nombres de Fibonacci et celle des carrés gnomoniques qui leur correspondent, relation constituant une application importante entre la théorie des médiétés et celle du gnomon.

Reconnaissons, toutefois, que cette construction aurait été encore plus belle et pertinente, si M. Brémaud avait disposé ses carrés en suivant la progression d’une spirale logarithmique, comme dans la figure ci-dessous : 

  

               

Dans cette application de la médiété au carré gnomonique, on remarque, en particulier, que les hypoténuses correspondantes aux carrés successifs de la suite de Fibonacci, se trouvent, elles aussi, en proportion « de Fibonacci ».

  

  

Si l’on prend pour exemple les hypoténuses correspondantes aux carrés de côtés 2, 3 et 5, on vérifie que :

(rac 50 – rac 18)  =  rac 8        =   2

(rac 50 – rac 8)        rac 18            3

Et l'on constate que le rapport a/b qui est le rapport mineur de la médiété (situé à droite du signe égal) est égal au simple rapport des côtés des carrés utilisés, - tout cela en application évidente du théorème de Pythagore.

Enfin, cette construction permet de tracer la spirale logarithmique correspondante à la suite des carrés, spirale rendue célèbre par ses multiples applications « florales » (pissenlit, artichaut, tournesol, etc).

  

   

  

  

*

  

On peut remarquer que la structure de la médiété Nicomaque 10 est constituée, dès l'instant où l'on a disposé les trois premiers carrés (carrés gnomoniques  de rangs 1, 1 et 2), formant ensemble un premier "rectangle de Fibonacci". Le rapport entre la longueur et la largeur du rectangle peut, dès cet instant, être considéré comme une première approximation du nombre d'or, certes grossière, mais qui ne cesse ensuite de se préciser à mesure que la taille du rectangle augmente.

Dans la littérature moderne, la contribution la plus importante, concernant cette médiété Nicomaque 10, me semble être celle de Roger Penrose, avec ses fameux "pavages de Penrose".

On peut dire que la démarche de Penrose est en quelque manière inverse de celle qui est illustrée dans la figure ci-dessus. Alors que, dans la figure ci-dessus, le nombre d'or est la limite vers laquelle tend la croissance du rectangle, dans un pavage de Penrose, ce même nombre d'or est la structure invariante que l'on pose au départ, sous la forme d'un premier triangle d'or, triangle qui, par des divisions successives, engendre un pavage continu non périodique, dans lequel on retrouve la suite des nombres de Fibonacci.

Le "rectangle de Fibonacci" et le "triangle d'or de Penrose" peuvent sans doute être considérés comme les objets géométriques les plus fondamentaux que l'on doive associer à la médiété Nicomaque 10. Entre ces deux objets s'opère un retournement, un retroussement, par lequel toute la nature mathématique se trouve transformée. En effet.

Alors que, dans le rectangle de Fibonacci, la suite de Fibonacci est une fonction de croissance, elle est, dans le triangle de Penrose, une fonction de division. Alors que le nombre d'or est, dans le rectangle de Fibonacci, le nombre correspondant à la position de l'infini, il est, dans le triangle de Penrose, le nombre correspondant à la position "1". Alors que ce qui est "Fibonacci" dans le rectangle de Fibonacci est le nombre de carrés (les nombres de Fibonacci  correspondant au nombre de carrés "atomiques" de valeur 1 que l'on peut dénombrer sur les côtés des rectangles successifs - largeur et longueur), ce qui est "Fibonacci" dans le triangle de Penrose est le nombre de triangles  (obtus et aigus). Le rectangle de Fibonacci contient l'infini, dans ce sens que deux rectangles de Fibonacci ne sont jamais semblables au sens mathématique (le rapport largeur/longueur n'est jamais le même), bien qu'ils soient de moins en moins différents; le triangle de Penrose contient l'infini sur un mode qui est celui de la non-périodicité, c'est à dire que le motif dessiné par un pavage de Penrose ne présente jamais de règle de répétitivité continue, de sorte qu'il est impossible d'en construire l'ensemble au moyen de la réplication d'une partie quelconque.

A ces diverses différences-symétries entre les deux structures, on peut ajouter cette dernière, plus profonde. Alors que, dans le rectangle de Fibonacci, la médiété Nicomaque 10 est une fonction de l'espace, qui s'accomplit dans le temps, dans le triangle de Penrose, la médiété Nicomaque 10 est une fonction du temps, qui s'accomplit dans l'espace.

  

Triangle d'or de Penrose

     

   

 

 La progression du nombre de triangles d'or, aigüs et obtus, est celle de la suite de Fibonacci. Au bout de quelques étapes, on obtient toutes les autres pièces permettant de construire des "pavages de Penrose", à savoir la paire  (fléchette / cerf-volant), et la paire (losange gras / losange maigre). Le triangle de Penrose, constitué de triangles d'or aigüs et obtus, est donc la formule la plus générale, dont dérivent par composition toutes les autres.

  

  *

 

Concluons par deux remarques à caractère plus aphoristique.

 

 Situation du pythagorisme.

Penrose considérait ses pavages comme une récréation mathématique, et n'attribuait pas à ce travail une importance comparable à celle de ses travaux mathématiques "sérieux". De nos jours, l'impact de cette découverte sur la science en général apparaît, au contraire, plus important que celui de ses autres travaux. Ce malentendu est tout sauf anodin, et traduit la situation "problématique" qui peut être celle du pythagorisme dans la science contemporaine.

  

 Le devenir physique des idées mathématiques pythagoriciennes.

 Les pavages de Penrose ont une symétrie d'ordre 5, pentagonale donc, qui était jusque récemment considérée comme interdite dans l'ordre très rigoureux qui est celui des "systèmes cristallins". Un cristal de symétrie pentagonale était considéré comme une impossibilité, parce que le pentagone n'est pas une solution de pavage du plan (et donc, ne peut permettre de construire une facette cristalline). Dans cet ancien paradigme, la contrainte de continuité était associée à la contrainte de périodicité. Au début des années 80, des quasi-cristaux de symétrie pentagonale, présentant toutes les apparences d'un cristal normal, et répondant aux caractéristiques mathématiques d'un pavage de Penrose (continuité non périodique), sont réalisés de façon synthétique*. En 2008, on découvre que, ce que la chimie venait d'accomplir, la nature l'avait déjà réalisé : un quasi-cristal naturel de symétrie pentagonale, probablement d'origine extraterrestre, est découvert en Russie. Ces divers événements ont contraint les manuels de cristallographie à modifier leur définition du cristal, afin d'y intégrer les quasi-cristaux de symétrie pentagonale. Pourtant, la cristallographie pouvait être considérée jusque là comme un département achevé de la physique : édifice entièrement prisonnier des lois de la symétrie, formulées aujourd'hui dans le cadre de la théorie des groupes. La cristallographie est, de fait, une espèce de dimension "témoin" de la physique, interface parfaite entre la structure invisible : les arrangements d'atomes, et la structure visible : la facette du cristal, et son angle au sommet, pure matérialisation de la géométrie des polyèdres.

Là encore, on n'est qu'à moitié surpris. Aujourd'hui comme hier, les idées mathématiques pythagoriciennes semblent affectées d'un certain "devenir physique". La mathématique pythagoricienne implique, parmi d'autres choses,  la recherche d'une certaine adéquation entre la nature mathématique, et la nature physique. Son objet la détermine à décrire, assez souvent, le genre de choses que la nature est susceptible, elle aussi, de réaliser.

 

Septembre 2012

 

*En 2011, Dan Shechtman s'est vu décerner le prix nobel de chimie pour ces travaux sur les quasi-cristaux.

  

              

 Quelques applications florales de la suite de Fibonacci

 

 

                                          

 Structure et aspect d'un quasi-cristal de synthèse

  

   

 

Météorite quasi-cristalline découverte en Russie en 2008

 

  

  

  

GLOSES  

  

 

1. Les médiétés de 1 à 0

 

 
On a vu que la médiété N1 pouvait être définie comme saturée sur un plan sémantique et logique, mais il est également possible de la reconnaître comme saturée sur un plan purement mathématique, puisque le rapport mineur de cette médiété a une valeur constante de x/x = 1, valeur qui coïncide avec l'extension maximale que peut prendre le rapport mineur d'une médiété, les rapports mineurs des autres médiétés pouvant tous s'exprimer par des rapports inférieurs à 1. Dans cette perspective, il peut être intéressant d'élargir notre définition habituelle de la médiété, en définissant le système dans N inclus zéro, et en stipulant qu'une médiété est une relation entre 3 nombres A, B, C, tels que A inférieur ou égal à B inférieur ou égal à C, dans laquelle deux de ces nombres sont entre eux dans le même rapport (mineure) que deux de leurs différences (majeure). On obtient alors 5 niveaux étagés entre 1 et 0.

Niveau 1. La position de référence est donc celle, saturée, de la seule médiété N1 (dite arithmétique) dont le pprm (plus petit rapport mineur possible) est égal à 1.

Niveau 2. Un ensemble de 5 médiétés dont le pprm est égal à 2/3. Ce sont les médiétés N6, N7, N8, N9 et T12. Ces médiétés, auxquelles je ne connais pas d'application géométrique remarquable, donnent l'impression de fonctionner toutes de la même manière et de pouvoir être reliées par une équation commune, de manière à ne former qu'une seule supermédiété.

Niveau 3. Quatre médiétés dont le pprm est égal à 1/2. Ce sont la médiété "géométrique" N2, les médiétés  N4 et N5, ainsi que la médiété T11, que l'on a déjà examinée en raison de son absence d'intérêt mathématique, son adoption se résumant à intégrer dans le système un axiome d'existence du nombre zéro.

Niveau 4. Une seule médiété N3, (dite "harmonique"), dont le pprm est égal à 1/3.

Niveau 5. Dans cette formulation, la position "saturée" qui répond symétriquement à l'autre extrémité du système (où l'envergure est "maximale", c'est à dire égale à 1) est donc occupée par la seule médiété N10 ("de Fibonacci"), dans laquelle le pprm est égal à 0/1 = 0. Puisqu'en effet, notre définition élargie permet d'admettre comme "plus petite solution possible" de la médiété la solution (0, 1, 1), et par suite comme pprm le rapport 0/1. Sur le plan logique, on ne peut donc pas avoir moins de 5 médiétés, semble-t-il.

Précisons que, dans ce raisonnement, on appelle pprm le rapport mineur simplifié, contenu dans la plus petite solution entière d'une médiété; c'est ce rapport qui comporte 5 degrés d'obturation entre 1 et 0. Ainsi, les médiétés du niveau 2 ont, dans leur plus petite solution entière, un rapport mineur égal à 4/6  ou 6/9 (= 2/3). Sur la table des médiétés du blog, les plus petites solutions entières sont reprises de Nicomaque, chez qui elles ne sont pas forcément justifiées par une définition explicite. Pour la médiété "de Fibonacci", Nicomaque retient comme première solution le triplet (3, 5, 8), sans doute pour éviter le triplet (1, 2, 3) qui serait identique à N1. Nicomaque semble donc favoriser la première solution originale d'une médiété; mais rien n'interdit de reformuler la table des solutions à partir d'une définition plus moderne de la médiété, et en privilégiant non plus la première solution originale, mais la première solution possible. Dans ce cas, il paraît donc avantageux de définir le système pour A inférieur ou égal à B inférieur ou égal à C, de manière à intégrer toutes les solutions initiales de la suite de Fibonacci, et notamment les 4 solutions qui précèdent celle retenue par Nicomaque, savoir : (0, 1, 1); (1, 1, 2); (1, 2, 3); (2, 3, 5); ...

   

 

 

2. Obturation du rapport mineur
 

 

La relation logique M (médiété), est une relation biternaire : x/y = M (A, B, C), où x et y doivent être choisis parmi les termes A, B ou C, et où M est le rapport de deux soustractions entre ces trois termes. Dans cette relation, le rapport mineur x/y représente donc le "côté" binaire de la relation.

Dans le système défini plus haut, on peut représenter l'obturation du rapport mineur par l'inscription d'un trépied, ou d'un triangle équilatéral, dans un cercle-unité. Les 12 médiétés se répartissent alors sur 4 positions, puisque les positions de N1 (arithmétique) et N10 (Fibonacci) coïncident, à ceci près que N1 correspond au cercle plein, et "Fibonacci" au même cercle vide. Les positions des médiétés peuvent ainsi recevoir une formulation "angulaire" qui est quaternaire; trois de ces positions correspondant aux sommets du triangle équilatéral, et la quatrième, celle de la médiété N2 (géométrique), étant déterminée par la médiatrice verticale du même triangle. La structure biternaire du système est donc bien apparente, même lorsqu'on ne considère que le rapport mineur. L'axe vertical correspond au côté binaire, le trépied au côté ternaire de la relation.

      

 

  

 

 

3. Table de correspondance

 

Cet article, pourtant simple, a suscité beaucoup de confusions, et notamment l’idée surprenante selon laquelle il pourrait exister des termes manquants dans une fonction mathématique. Il a donc paru utile de dresser une table de correspondance entre les deux structures. 

Il existe, bien évidemment, deux fois plus de rectangles de Fibonacci que de triangles de Penrose, puisque le rectangle de Fibonacci développe les nombres de Fibonacci par paires conjointes, alors que le triangle de Penrose développe ces mêmes nombres par paires disjointes. 

 

 

La série des triangles de Penrose correspond uniquement aux étapes impaires de la série des rectangles de Fibonacci.  Dans le rectangle de Fibonacci, les nombres de Fibonacci correspondent au rapport de la largeur à la longueur (l/L). Le « rectangle de Fibonacci » de rang 1, est donc un « rectangle » de largeur zéro et de longueur 1, c'est-à-dire un segment de longueur 1. Le rectangle de  Fibonacci de rang 2 est un « rectangle » de 1x1, autrement dit le carré atomique de côté 1 (qui permet ensuite de calculer déductivement, visuellement, les valeurs de tous les carrés suivants).  Au rapport (largeur/longueur) du rectangle de Fibonacci, correspond, une fois sur deux, le rapport (triangles obtus/triangles aigus) qui décrit la composition du triangle de Penrose. 

On se convaincra, au vu de ce tableau, que les deux fonctions sont bien complètes, et parcourent la série entière des nombres de Fibonacci, de zéro à l'infini; en précisant que, dans cet article comme dans d'autres, on emploie, par commodité, le terme "infini" dans le sens hyperbolique qui est celui de la mathématique moderne, pour désigner différentes variétés de l'indéfini.

 

 

 

  

  

4. Pentagone de Padovan

  

Si on le considère maintenant, non plus sous le seul angle de sa relation avec la médiété Nicomaque 10,  mais d'un point de vue plus général qui est celui de la théorie des polygones gnomoniques, le rectangle de Fibonacci possède une structure jumelle qui est le pentagone de Padovan.

Alors que le rectangle de Fibonacci est formé de carrés gnomoniques, le pentagone de Padovan est formé de triangles gnomoniques. A chacune de ces structures sont associés une suite arithmétique et un nombre (irrationnel) remarquables (au nombre d'or, phi, de la suite de Fibonacci répondant le nombre "plastique", psi, de la suite de Padovan), ainsi qu'une spirale logarithmique. De la même manière que, dans le rectangle de Fibonacci, le rapport entre les côtés tend vers phi, dans le pentagone de Padovan, le rapport entre deux côtés successifs du pentagone tend vers psi.

 

  

 

 

La suite de Padovan, en revanche, ne relève pas de la théorie "classique" des médiétés à 3 termes, mais d'une théorie plus générale comprenant les médiétés à 4 et 5 termes, ou plus, domaine qui reste largement inexploré si l'on excepte l'étude, par Nicomaque notamment, de la médiété "parfaite", ayant pour plus petite solution le quadruplet (6-8-9-12).

La médiété ci-dessus, qu'on appellera médiété de Padovan, peut, par exemple, être définie comme une relation entre 5 termes : a, b, c, d, e, chacun étant inférieur ou égal⁽¹⁾ à son successeur, dans laquelle on a ces trois identités :

a + b = d

b + c = e

(a + e) = (c + d)

Les cinq termes correspondant aux cinq triangles gnomoniques qui sont suffisants pour délimiter la circonférence de n'importe quel pentagone de Padovan. Dans l'exemple illustré ci-dessus, les termes a, b, c, d, e, correspondent (pour le plus grand des pentagones) aux triangles gnomoniques de rangs : 7, 9, 12, 16 et 21.

Gérard Cordonnier a défini cette médiété en utilisant la méthode euclidienne de division d'un segment en "extrême et moyenne raison", qui permet de définir le nombre d'or. 

  

  

Pour le nombre "plastique", le segment est divisé en trois parties, qui déterminent elles mêmes par combinaison trois autres grandeurs; ces six segments étant tous ordonnés en proportion géométrique. Gérard Cordonnier montre que la proportion géométrique est de valeur : "psi"; ce qui signifie que, tout comme une grandeur peut être "double" ou "triple" d'une autre, chaque segment est ici le "psi-uple" du précédent.⁽²⁾

On voit que les deux méthodes, géométrique et "algébrique", sont équivalentes, puisque tous ces rapports de grandeur sont déductibles des trois identités formulées plus haut. Les segments 1 à 5 correspondent aux termes (a, b, c, d, e) de la médiété, quant au sixième, il correspond au terme "f", terme qui est donc le "successeur immédiat" de la médiété, et qui est toujours égal à (a + b + c) comme cela ressort également de nos trois formules.

  

⁽¹⁾ La mention "inférieur ou égal" permettant, comme pour la suite de Fibonacci, de faire débuter la suite de Padovan à zéro, et d'attribuer pour valeurs au pentagone de Padovan de rang 1, le quintuplet : (0, 1, 1, 1, 2). La série se développe ensuite par quintuplets immédiatement successifs, le pentagone ci-dessus occupant  le rang 10.

⁽²⁾ La très grande généralité de la médiété géométrique fait qu'elle joue ici le rôle de substrat, ou de "paradigme", dans la définition d'une médiété d'ordre moins primitif.

 

 

 

 

 

 

SPIRALE DE THEODORE

ET

POLYGONE GNOMONIQUE DE RANG 4

  

  

  

Le 27 août 2012 à 12h17, j'ai reçu sur le blog le message suivant de M. Axel Schneider. Si toutes ses remarques sont intéressantes, celle qui concerne la spirale de Théodore est d'ordre fondamental. En effet, la spirale de Théodore est tout simplement la structure duale du polygone gnomonique de rang 4.

A. Schneider :

Côté du carré de Vitruve / rayon cercle Vitruve = 8/5 unités (écart entre centre cerle et celui carré). Ce rapport est celui du flocon de Koch et 2 nombres de Fibonacci. Surtout on a 2 rectangles = le carré long de 3/4 et diagonale 5 et son complément de 4/1 et diagonale racine 17 (comme dans la spirale de Theodorus).

5 et 17 : 1!+...+5!=1+...+17=153
« Amis, leur dit-il, voulez-vous parier avec moi que je puis vous révéler à l’avance, le nombre exact des poissons que vous venez de capturer ? » Vie de Pythagore de Jamblique.

E. Post avait pour ambition de trouver dans quelle mesure une théorie capable de formaliser l'arithmétique, partiellement récursive (ratio) pouvait être à la fois consistante et complète (mesure de l'incomplétude).

Je pense comprendre pourquoi il évoquait le flocon de Koch avant de mourir avec Koch. C'est une question pythagoricienne et la solution est dans Vitruve.

1531 suite Cunningham : J'ai besoin de vos connaissance sur le gnomon qu'i...

Le message de M. Schneider s'interrompt à cet endroit. 

 *

 

LA SPIRALE DE THEODORE EST LA STRUCTURE DUALE DU POLYGONE GNOMONIQUE DE RANG 4.

 

Spirale de Théodore

 

Polygone gnomonique de rang 4. (On prend ici l'exemple du carré, mais tout ce qui s'applique ici au carré gnomonique s'applique, par extension, au triangle gnomonique de même rang, puisqu'il existe entre ces deux structures une règle de transformation constante. A ce sujet, voir Blog 1 : gnomon d'un polygone régulier).

 

Le PG (polygone gnomonique) de rang 4 compte 16 blocs, la spirale de Théodore 16 blocs.
 
Le PG de rang 4 est une structure qui permet de déployer les carrés des nombres entiers de 1 à 4, ces carrés se déployant dans l'intervalle compris entre 1 et 16.

Symétriquement.
 
La spirale permet de déployer les racines carrées des nombres entiers de 1 à 16. (La racine 17 ne doit pas être prise en compte dans l'analyse de la structure, puisque le bloc 16 doit être traité comme le 1, en les coordonnant par leur origine, comme on referme un éventail; la racine 17 n'est donc que le bord extérieur de la structure) ⁽¹⁾ - racines carrées des nombres  1 à 16 qui elles-mêmes, se déploient dans l'intervalle compris entre  1 et 4. 

La spirale de Théodore est donc une application immédiate de la clôture à quatre; elle n'est même qu'un redéploiement de la structure qui est celle du PG de rang 4. Cette structure vient donc s'ajouter à la liste de celles qui sont immédiatement déductibles des propriétés mathématiques de la tétractys.

La spirale de Théodore est la structure duale du PG de rang 4, du fait que l'opération : "racine carrée de n" est l'inverse de l'opération "carré de n". L'équation complète me paraît être la suivante : le polygone gnomonique de rang 4 est à l'égard des carrés des nombres 1 à 4, ce que la spirale de Théodore est à l'égard des racines carrées des nombres entiers, dont les solutions sont comprises entre 1 et 4. Soit, en généralisant :

ST = D (PG).  (Où : ST : spirale de Théodore. PG : polygone gnomonique. D : "duale de ..." - dualité définie comme une application biunivoque sur l'ensemble des entiers.) ⁽²⁾

*

  

Une autre remarque de M. Schneider est également des plus intéressantes : celle qui consiste à décomposer le carré gnomonique de rang 4 en 4 triangles rectangles : soit deux triangles de valeur (3-4-5) et deux autres de valeur (1-4-racine17).

 

En effet ces deux triangles sont fondamentaux en ce que chacun d'eux correspond à un seuil de clôture.

Le triangle (3-4-5) est le plus petit des triplets pythagoriciens.

Le triangle (1-4-racine 17) est le plus grand des triangles de Théodore.

Les valeurs des aires de ces quatre triangles sont respectivement de : 6, 6, 2 et 2, et le rapport du triangle de Théodore au triangle (3-4-5) est de 1/3, - rapport qui n'est autre que celui du gnomon (g/G = 1/3 ; où g : graine, et G : gnomon).

* 

A ce sujet, remarquons que les modernes (comme c'est déjà le cas de Platon dans son Théétète) sont incapables d'expliquer pourquoi Théodore s'est arrêté au 16 ème bloc. Ils continuent de penser que Théodore s'est arrêté là pour des raisons esthétiques, parce que l'ajout d'un 17 ème triangle aurait eu pour effet de recouvrir le début de la figure.

En pythagorisme, ce qui se passe en deça de la clôture à 4 est fondamentalement différent de ce qui se passe après; et la clôture elle-même a le statut d'un seuil ou d'une coupure épistémologique. Seul ce qui se passe en deça de la clôture revêt une valeur axiomatique et fondamentale.

Citons pour conclure le Théétète : "Théodore nous avait expliqué, avec les figures, quelque chose de ce qui concerne les puissances, nous faisant voir, à propos de celles de 3 pieds et de 5 pieds, que, en longueur, elles ne sont point commensurables avec celle de 1 pied, les prenant ainsi une à une jusqu'à celle de 17 pieds. Mais, je ne sais comment cela se fit, il s'arrêta à cette dernière." (Traduction de Léon Robin).

 *

D'après ce que je comprends du message de M. Schneider, son sentiment personnel est que les divers éléments de ce dossier ont une importance de premier ordre, puisqu'ils pourraient permettre une résolution du problème d'Emil Post qu'il nous résume en ces termes : montrer "dans quelle mesure une théorie capable de formaliser l'arithmétique partiellement récursive, pourrait être à la fois consistante et complète".

Je lui souhaite bonne chance dans sa recherche.

 

29 Août 2012

 G. DENOM

 

 

 

⁽¹⁾ C'est évidemment pour la même raison que le nombre 17 correspond, dans un polygone gnomonique de rang 4, à l'axe de symétrie logique de la structure,  par application en miroir de la valeur ordinale des 8 premiers blocs sur celle des 8 derniers, considérés à la fois comme leurs symétriques et leurs négatifs : (1+16 = 2+15 = 3+14 = ... = 8+9 = 17), - quelle que soit la méthode géométrique à laquelle on puisse recourir pour déployer cette symétrie dans l'espace du plan; - et qu'il est, dans la spirale de Théodore, le bord ou le zéro géométrique. Le nombre 17 correspond simplement, dans ces deux structures, au retour logique de la position zéro induit par la clôture de la tétractys. C'est selon un principe semblable qu'est construit le carré magique de la Melancholia de Dürer, où le zéro logique est, cette fois, le nombre 34 (17+17). Pour cette construction, la chaîne des nombres a été simplement "pliée en deux" une fois supplémentaire, de manière à passer, arithmétiquement, d'une symétrie en V à une symétrie en W.

⁽²⁾ Pour que cette application prenne toute sa valeur, le carré gnomonique de rang 4 doit lui-même être construit par un mouvement spiral, à partir de l'un des quatre carrés situés en son milieu. De cette manière, on s'aperçoit que les étapes de reconstitution gnomonique du carré (respectivement de rangs 2, 3, 4, etc.) correspondent ordinalement, dans la spirale de Théodore, aux racines carrées des nombres 4, 9, 16, etc, qui ont précisément pour solutions les nombres 2, 3, 4, et ainsi de suite.

 

 

 

 

 

 

LA DIVINE DISTANCE

 

 

par Axel SCHNEIDER

 

  

Pour la commodité du lecteur, on a regroupé sous ce titre les six commentaires postés en septembre 2012 par Axel Schneider, à la suite de l’article : Spirale de Théodore et polygone gnomonique de rang 4. Ceux qui voudraient en savoir plus sur les idées de M. Schneider, et notamment sur la nature de ce fameux ratio mesurant, selon lui, une limite indépassable de la connaissance humaine, pourront se rendre avec profit sur le site personnel de l’auteur :

www.maformulederamanujan.org

 D'autres précisions sur le site de "l'homme de Vitruve" :     

http://screencircles.wordpress.com/2008/01/03/lhomme-de-vitruve/

 

 

 

1.

 

Mardi 4 Septembre 2012

 

En fait, je suis d'accord avec toi pour dire que tous les gnomons sont équivalents quand on considère les polygones réguliers. Le problème vient du cercle (ou plus exactement du disque) : ce n'est pas un polygone avec une infinité de cotés ou en tous cas pas plus qu'un polygone avec un seul côté. 

Dès lors, oui, le gnomon est bien la notion archaïque, sauf qu'elle nous conduit à affirmer avec Gödel que épistémologie/ontologie est inférieur strictement à 1. La question est de savoir quel est ce ratio… Cela ne concerne pas seulement les mathématiques, mais toute connaissance humaine ou surhumaine. Ce ratio ne peut être dépassé que par un concept que l'on peut appeler Dieu ou Oracle (comme Turing) mais qui pour moi n'a aucune vérité en soi, à moins de considérer que la connaissance de ce ratio confère a celui qui la détient cette vérité complète.

Nicolas de Cues était le précurseur de Gödel quant à propos de la question de la transcendance de pi (la quadrature du Cercle), il affirmait :

"(ceux) qui ont cherché la quadrature du cercle ont présupposé la coïncidence du cercle et du carré dans l’égalité, laquelle n’est assurément pas possible au niveau sensible. Car il n’existe pas de carré qui ne soit inégal à n’importe quel cercle engagé dans la matière. Cette égalité, qu’ils ont présupposée, ils ne l’ont donc pas vue avec leurs yeux physiques, mais avec leurs yeux mentaux, et s’ils ont essayé de la démontrer par le raisonnement, ils ont cependant échoué, puisque la raison n’admet pas la coïncidence des opposés. C’est intellectuellement qu’ils auraient dû chercher la coïncidence dans ce cercle qui est égal dans chaque polygone "

C'est la même chose que de dire que tous les gnomons sont identiques. Sauf que dès lors il faut admettre une incomplétude, une dualité du gnomon dans la mesure où le choix canonique entre la factorielle de 0,  0!=1 et 0!=-1 n'est pas symétrique au choix canonique entre i^2=-1 et i^1/2=-1. Il existe un isomorphisme entre le gnomon des réels et le gnomon des imaginaires, mais le gnomon complexe n'est pas atteignable sans une "approximation"  (le foncteur d'oubli du plan complexe considéré comme une surface de Riemann universelle).

 

 

2.

 

Mardi 4 Septembre

 

Seul compte le corps des complexes, la clôture algébrique du corps des réels sur le corps des nombres imaginaires : c'est l'unique représentation possible de l'espace sensible et, comme je l'ai dit, sur cet espace sensible, le gnomon "complexe" est obligatoirement dual, c'est à dire que le gnomon "véritable" n'est pas accessible au sensible. 

Cela se décline selon moi : avec l'inégalité isopérimétrique (rappelez vous de la création de Carthage par Didon...). Dans ce cadre, le cercle et le triangle équilatéral sont des extremums : le cercle est le "polygone" qui par rapport au "périmètre" (circonférence) a la surface la plus importante et le triangle équilatéral celui qui pour le même périmètre a la plus petite surface. Le carré est donc le premier polygone et permet de calculer le cycle d'obstruction... C'est ainsi que l'on trouve la construction de Vitruve.

On a alors en reprenant votre logique 2 carrés gnomiques et non un seul (car alors le centre du cercle et le centre du grand carré vitruvien sont distants d'une unité). Le carré gnomon de rang 5 qui se décompose en 2 rectangles : l'un de 4 sur 1 et de diagonale racine 17 et l'autre de 4 sur 5 et de diagonale racine de 41, et le carré gnomon de rang 4 qui se décompose alors en 2 rectangles, le rectangle de 4 sur 1 (le même que précédemment) de diagonale racine de 17 et le rectangle pythagoricien (triangle isiaque) de 3 sur 4 et diagonale 5.

 

 

La tradition compagnonique reprise par les traditions maçonniques, considère le problème ainsi : on ne peut pas mieux faire comme polygone gnomique complexe que le carré long de 3 sur 4. Donc, dans ces traditions le fameux ratio correspond à la surface du carré long divisée par la surface du carré possédant le même périmètre de 14. On trouve ainsi un ratio de 12/12,25 soit un peu plus de 97 %. L'incomplétude dans cette logique serait donc d'un peu plus de 2 % seulement... C'est très faible (et donc forcément très subversif pour les Eglises) et en même temps très important pour les positivistes car, cet univers platonicien nous est bien inaccessible (mais l'on saurait si cela est exact à quelle divine distance de nous il se trouve).

Je ne serai pas plus long pour le moment, mais il faut bien comprendre le phénomène d'obstruction : c'est la parabole de la pêche miraculeuse partagée par Pythagore selon Jamblique et par le Christ selon Saint Jean (tiens le Christ aurait reçu un enseignement pythagoricien? Peut-être est-ce le fils d'Isis et d'Amon-Osiris comme pouvait l'être, par exemple, Césarion-Horus...) Les poissons ce sont les vesica piscis, 1/2 de la racine de 3, les mailles du filet, le polygone gnomique de rang 4 : reste toujours 153 = 1!+...+5! = 1+...+17...

 

 

3.

 

Mardi 4 Septembre

 

Tout d'abord, diverses représentations du carré long de 3 sur 4 dans les traditions maçonnique et chrétienne : 

 

               

                    

  

Et le double centre de la construction de Vitruve chez les Templiers :

  

 

  

4.

 

Mercredi 5 Septembre

 

Votre remarque sur la conception Euclidienne, "le point est ce qui n'a pas de parties" et celle plus monadique (dans le sens de Leibniz) de Pythagore "10 points sont montrés ou présentés dans la pensée" (le Tetracktys) est particulièrement bien venue. 

Etienne Klein, physicien spécialiste de la question du temps, a bien fixé le cadre qui a animé de vives discussions entre Stephen Hawking et Roger Penrose en 1997 sur la Relativité générale. En effet, le cadre théorique relationnel de la RG (continuum espace-temps), puisqu'il ne peut jamais être "vide" absolument : il existe toujours un tenseur métrique, un champ qui ne s'annule jamais "en tout point" du continuum. Comme les équations de Maxwell traitent du champ électromagnétique, les équations d'Einstein traitent de ce champ. Ainsi la RG, qui se veut une vraie théorie par rapport à l'approche de Newton qui retient l'espace et le temps comme des absolus (je dirais même la matière et donc la gravité), n'existe pas sans sa métrique. Or pour définir un champ, il faut définir ce champ : l'approche pythagoricienne du Tetracktys me semble tout a fait adaptée puisqu'il s’agit comme vous le dites d'un ensemble de 10 points, un champ logique. Le tenseur métrique ne s'annule en aucun point "euclidien" : en clair, pas d'annulation, pas de singularités (style trou noir) dans la RG car sinon il faut considérer la disparition de la métrique. Sauf à considérer, comme le très pythagoricien (selon moi) Aristote, que le 1 n'est pas un nombre mais une idéalité platonicienne inatteignable...

 

 

5.

 

Mercredi 5 Septembre

 

Je trouve très intéressante l'idée de dire que quel que soit le polygone régulier envisagé, eh bien le gnomon est "équivalent" (à n-près) et de parler de polygone gnomique plutôt que de gnomon.

C'est comme l'approche pythagoricienne de N. de Cues qui affirme qu'il n'existe "pas de carré qui ne soit inégal à n'importe quel cercle". Il ne dit pas que la quadrature du cercle est possible, il dit juste que comme le cercle (disque) partage avec le carré (et donc tout autre polygone régulier) les concepts de longueur (D1) (circonférence) et de surface (D2) (aire), eh bien intellectuellement ils sont "égaux" mais que cette similitude n'est pas perceptible au niveau "sensible". Je pense que dans l'esprit de N. de Cues, en tous cas dans celui de L. de Vinci et de la "petite école cusienne d'Italie" eh bien la cause de l'impossibilité d'une quadrature était acquise, bien que la démonstration ne viendra qu'au 19ème siècle. Dans l'esprit "cusien", la transcendance (le mot est anachronique) de pi n'est donc pas le signe d'une "inégalité" mais d'une obstruction, une homologie ou plus exactement une cohomologie (là encore ce sont des anachronismes), c'est à dire l'obstruction qu'ont certaines suites de morphismes (deux ensembles avec une même structure comme par exemple dans le cas d'espèce les polygones et les cercles) à être exactes.

Ainsi le raisonnement que l'on fait sur le carré est valable à n-près pour n'importe quel polygone régulier (du triangle équilatéral au polygone avec une infinité dénombrable de cotés). 

Attention ! Je dis bien un polygone avec une infinité dénombrable (au sens de Cantor donc avant diagonalisation vers l'infini indénombrable des Réels) de côtés. Dans mon idée, un polygone avec une infinité indénombrable de côtés, c'est un cercle.

L'idée de rajouter l'hypothèse du continu (ou du discret) à l'ensemble des axiomes d'une théorie formelle capable de formaliser l'arithmétique et récursivement axiomatisable (logique du 2nd ordre) ne change rien au fait qu'elle contient des propositions contradictoires (consistance) ou indécidables (complétude). Il résulte en fait des travaux de Gödel de 1938 et de Paul Cohen de 1963 (avec sa célèbre méthode de Forcing) que l'hypothèse du continu est indécidable. Donc, pas plus de complémentation avec l'axiome du continu qu'avec n'importe quel axiome (comme l'axiome de protection de la chronologie de Stephen Hawking pour la relativité générale...). Ainsi, on ne sait pas si il y a des trous ou non dans la droite réelle, c'est à dire si le cardinal transfini de l'infini indénombrable des réels (aleph 1) est le successeur immédiat du cardinal transfini de l'infini dénombrable (aleph 0).

L'idée de l'angle d'attaque est donc de dire (un peu comme l'intrication quantique) qu'au niveau "sensible" (au sens de N. de Cues), eh bien il faut considérer que les 2 sont vrais et que l'on ne peut pas calculer le cardinal aleph 1/2 soit parce qu'il n'existe pas et que la relation d'ordre entre aleph 0 et aleph 1 est "séparée" par rien ou plus exactement un objet qui n'est pas défini dans les mathématiques, soit parce que l'on ne peut connaître la position absolu de aleph 1/2, les trous dans la droite réelle n'étant alors pas calculables exactement.

Ces deux hypothèses au niveau "sensible" sont donc identiques en dernière analyse... Mais, il y a selon moi un mais, puisqu'au niveau "sensible", on démontre en tous cas des "trous" logiques (qu'ils soient virtuels ou réels) et peut-être que l'on peut calculer l'importance de ces trous à défaut de les situer.  

J'ai déjà montré comment Léonard de Vinci (et bien entendu Vitruve) envisageait la question : c'est l'unité isopérimétrique. On a beaucoup dit que l'homme vitruvien était la représentation des mensurations de l'homme idéal... Oui et non : la perspective de Vitruve c'est de mesurer la "divine distance", c'est à dire "si" "Dieu" a fait l'homme à son image (parfaite), dans quelle mesure l'homme (ou Dieu par récursivité...) peut-il appréhender la "pensée divine" (la vérité). Vitruve parle de cela d'ailleurs dans la partie de son "de Architectura" consacrée à la construction des temples (comme le mythe compagnonique et franc-maçon de la construction du temple de Salomon : l'équerre et le compas avec la question du centre de gravité G). Vitruve (et le Vinci) veulent mesurer ainsi le rapport entre l'ontologie (la sémantique) et l'épistémologie (la syntaxe), la "divine distance".

Voilà l'idée de Vitruve... et celle d'Emil Post : mesurer le RE Turing degree universel, que l'on peut formuler selon moi ainsi : "Quel est le plus petit x qui permet d'avoir une théorie capable de formaliser l'arithmétique (structure algébrique ternaire), récursivement axiomatisable à 100 %, consistante et complète au sens de Gödel?"

 

 

  

Le centre du cercle, et celui du carré : dans la construction de Vitruve on retrouve l'"égalité" de N. de Cues c'est à dire que le rapport entre le côté du carré et le rayon du cercle quand on les met dans une relation triangulaire (puisqu’on ne peut distinguer entre les 2 extremums du triangle équilatéral - minimun isopérimétrique dénombrable - et le cercle maximum isopérimétrique indénombrable) est de 8/5 unités, l'unité étant la "distance" entre le centre du cercle et celui du carré (la métrique qui ne s'annule en aucun point de l'espace-temps relativiste...)

Bon et quid du Gnomon ?

Le Gnomon c'est 2n+1. Mais, pour les nombres imaginaires ? 2n-1.

Maintenant, sur le plan complexe ? Et bien, c'est là où l'unité du Tretracktys : le Tretracktys en tant que théorie formelle ne peut servir à axiomatiser complètement la "théorie formelle" (méta-modèle) et donc conceptualiser complètement le gnomon complexe.

L'unité gnomique de référence est donc le gnomon de rang 4, le gnomon quadratique. On ne peut aller en dessous. Ainsi on a une rupture de symétrie entre la plus petite chaine de Cunningham (chaîne de nombres premiers) de type 1 (2n+1) et de poids 5 (4 itérations) : 2, 5, 11, 23, 47 et  la plus petite du type 2 (2n-1) et de même poids qui commence par 1531 :

1531 3061 6121 12241 24481

Pourquoi ce 1531 : car 1!+...+5! = 1+...+17 = 153

Rappelons que la somme infinie de l'inverse des factorielles nous donne le nombre e, base des logarithmes népériens. Mais contrairement à ce que pourrait laisser penser l'identité d'Euler eî.pi = -1 (donc Dieu existe disait Euler à Diderot à la Cour de la Grande Catherine...) : la transcendance de e et de pi ne sont pas forcément équivalentes dans le sens où l'on peut avoir des nombres transcendants comme e avec une mesure d'irrationalité  égale à 2 comme pour les irrationnels algébriques (par exemple les racines des nombres premiers). On ne connait pas la mesure d'irrationalité de pi (enfin moi je crois que si : on prend juste mon ratio et 2+2*2,08 %).

Ainsi, si effectivement les log naturels permettent de faire d'une multiplication une addition, on peut montrer la convergence vers pi de la moyenne arithmético-géométrique (AGM) de 1 et 1/racine de 2 (cf. la formule de Brent-Salmin).

 

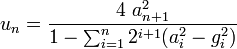
Sauf que la vitesse de convergence de la somme des inverses des factorielles vers e est peut-être plus rapide que la convergence de la moyenne AGM de 1 et de 1/racine de 2 vers pi.

(la suite prochainement)

 

 

6.

 

Vendredi 14 Septembre

 

La recherche des bonnes proportions entre le diamètre des colonnes des temples et leur hauteur a conduit dans la Grèce antique aux différents ordres architecturaux (on en recense 5 traditionnellement mais les plus importants sont les ordres dorique, ionique et composites). La question qui se posait était bien évidemment la quadrature du cercle.

 L'ordre Dorique semble privilégier le carré "vitruvien" plutôt que le cercle "vitruvien" : 8 plutôt que 10. A l'inverse, l’ionique privilégie plutôt le 10 par rapport au 8. Les ordres composites "tâtonnent" entre ces 2 extrêmes. Vitruve nous montre que la divine proportion n'est atteignable que de façon approximative (le carré long).

  

  

 

 

 

 

FOI RELIGIEUSE OU FOI SCIENTIFIQUE ?

  

par G. Denom

  

    

 

Ce texte est la synthèse de deux lettres que j'ai écrites dans le cadre d’un échange avec Jean-Luc Périllié, maître de conférence en philosophie ancienne à Montpellier, et auteur de Symmetria et rationalité harmonique, origine pythagoricienne de la notion grecque de symétrie. Ce livre, paru en 2008, montre la richesse et l’universalité de la notion pythagoricienne de symétrie, dont l’acception est plus large que la définition moderne, puisqu’elle signifie au sens propre commensurabilité, commune proportion des parties d’un tout, entre elles aussi bien qu’à l'égard de ce tout. Cette notion qui, non seulement, est intimement liée à la théorie des médiétés, mais qui peut aussi, plus profondément,  être considérée comme un arrière-plan paradigmatique, commun aux quatre concepts fondamentaux de la mathématique pythagoricienne, et essentiel à chacun d'eux; - cette notion si importante donc, en raison pythagoricienne, n’avait, jusque là, jamais fait l'objet d'une étude systématique.

Mais la discussion, ici, se rapporte davantage à l’objet du  travail actuel de Jean-Luc Périllié, qui est, pour citer une de ses lettres "de préciser les liens entre pythagorisme et cultes des mystères, en s'appuyant principalement sur les renseignements que l'on trouve dans une source assez ancienne et abondante : les dialogues de Platon, et dans la perspective ouverte par l’étude très forte et brillante de Peter Kingsley sur : Empédocle et la tradition pythagoricienne."⁽¹⁾

  

*

 

Qu'est ce que l'oracle de Delphes? C'est la tétractys, qui est l'harmonie dans laquelle vivent les Sirènes. 

Acousmates, Vie pythagoricienne, Jamblique. 

  

 

  

"Penseur religieux" et "mystique" sont des attributs que l’on voit souvent associés au nom de Pythagore. Le principal problème que je vois à leur emploi, c'est qu'ils sont presque toujours utilisés sans être définis. Or pour un chrétien, ces notions sont attachées à certaines représentations assez précises, qui n'ont pas forcément d'analogues dans le monde antique.

En vue simplement de sortir de l'indéfinition, je propose une définition approximative. Dans le monothéisme, le mot religion désigne une relation collective et universelle à un être absent ou abscons. La mystique, elle, est la réunion d'un être exceptionnel avec la présence divine, inaccessible au commun. Ces représentations précises, dans lesquelles ces deux notions s'explicitent très bien et se complètent l'une l'autre, me paraissent décrire un modèle de religion qui ne vaut, en réalité, que pour les trois grands monothéismes,  mais qui est, finalement, assez peu pertinent pour les cultes antiques.

*

  

Ce n'est pas moi qui reprocherais aux historiens d'accorder de l'importance à l'aspect religieux du pythagorisme, puisque l'un des principaux griefs que j'aie contre les historiens du pythagorisme (surtout ceux opérant dans la filière de l'histoire des sciences et de la mathématique ancienne) est leur méconnaissance des faits religieux, qui s'aggrave, d'ailleurs, à mesure que ces faits sont plus anciens. Ce reproche pourrait du reste s'adresser aux intellectuels modernes dans leur généralité. Il existe des gens que l'on nous présente comme "pointus" dans leur domaine  de compétence, pour qui la religion est une espèce de disposition mentale un peu naïve, qui vous rendrait peu apte, par exemple, à l'exercice de la  science. Des notions aussi grossières de la religion, même pas dignes du niveau d'un  journal télévisé, sont aujourd’hui monnaie courante. Un autre travers du même genre, est celui qui consiste, lorsqu'on prononce les mots de  mystère  ou d'initiation, à les accompagner d'une sensation d'interdit ou de frisson, aussi ridicule que possible.

*

  

Commençons  par énoncer une série de propositions parfaitement triviales, qui ne sont intéressantes que par les gloses qui les accompagnent et qui en définissent aussi exactement que possible la portée.

1. Les pythagoriciens, et Pythagore lui-même, pratiquaient des cultes religieux. C'est là un attribut qu'ils partageaient avec l'ensemble des hommes de l'antiquité.

2. Les pythagoriciens, et Pythagore lui même, pratiquaient des cultes exotiques. C'est là un attribut qu'ils partageaient, au moins, avec une grande partie de la classe cultivée du monde grec, pour laquelle la religion "commune", ou populaire, apparaissait comme trop dégradée pour permettre, à elle seule, une véritable élaboration théologique. Les anciens n'opposaient pas leur culte religieux à ceux des autres, puisqu'ils pensaient que les dieux des autres peuples n'existaient pas moins que les leurs. La comparaison des dieux d'un panthéon national, avec ceux des peuples voisins, était donc, dans le monde ancien, un simple exercice de théologie ordinaire. D'où le risque, pour le moderne qui s'attarde à ces analogies, à ces correspondances entre différents cultes, d'une véritable  hémorragie de signification religieuse, qui permet par exemple à certains, sans beaucoup d'effort, de voir dans le Pythagorisme un mélange de chamanisme hyperboréen, d'apollinisme, de dyonysisme, d'orphisme, sans exclusion de la théologie égyptienne, du mazdéisme, du zoroastrisme, du brahmanisme et bien sûr du druidisme.

3. Quand bien même on parviendrait  à une description plus précise. Par exemple : les pythagoriciens étaient une secte orphique. Ou encore : le pythagorisme est une nouvelle formulation du chamanisme hyperboréen, on n’aurait rien obtenu de fondamentalement nouveau par rapport au niveau 1. Les initiations, les mystères, même s'ils étaient réservés à de petits groupes, ne constituaient qu'un niveau supérieur de cette dimension du religieux qui était une dimension ordinaire et normale de la vie humaine, de toute vie humaine.

Le risque qu’il y a ici, c'est celui de chercher une correspondance entre deux plans de réalité qui n'ont, a priori, pas de rapport intrinsèque. Par exemple : Adam Smith et Ricardo sont les fondateurs de la pensée libérale. Adam Smith et Ricardo étaient de religion anglicane. Donc, le libéralisme est une secte religieuse affiliée à l'anglicanisme. L'exemple est bien sûr exagéré, cependant, il indique bien le profond sophisme qu'il peut y avoir à mettre sur le même plan un événement singulier et extraordinaire de l'histoire, tel que la naissance du libéralisme, avec des faits parfaitement ordinaires à tous les hommes d'une même époque; et le sophisme est à peu près le même dans le cas du pythagorisme, où il n'y a pas plus de raison  a priori de relier un événement aussi extraordinaire et singulier que l'apparition de la doctrine de Pythagore, ses concepts, ses réalisations scientifiques et intellectuelles, avec un plan parfaitement ordinaire  et pour ainsi dire "neutre" de la vie de son temps, qui est celui de la religion.

*

  

Quand bien même on réussirait à rendre aussi précise que possible une définition relevant du niveau 3. Par exemple : "les pythagoriciens étaient une secte orphique", ce serait là, j'en conviens, une information historique intéressante, mais on n'aurait toujours pas commencé à parler de la foi propre qui caractérise les pythagoriciens en tant que pythagoriciens. Or sur ce point là, il y a une pièce sur laquelle la décision est impérative : c'est le serment pythagoricien.

Si le serment est authentique, s'il remonte au premier groupe pythagoricien, alors la foi pythagoricienne n'est autre que la foi scientifique, elle n'est autre que la foi du mathématicien en son théorème, cette "bonne" foi, qui n'implique que l'attachement à son propre signe, et qui, dans le paradoxe logique du même nom, s'oppose à la "mauvaise" foi qui est celle du menteur, - cette foi que j'ai appelée dès ma jeunesse la foi de Spinoza, et qu'il professait à ceux de ses correspondants qui lui demandaient comment il pouvait être certain de ses thèses :  je le crois comme je crois que les trois angles d'un triangle sont égaux à deux droits. En effet, dans le serment pythagoricien, on ne vous demande pas de croire en une entité absconse ou absente, mais dans une réalité qui est présentée dans la pensée : la tétractys. Après cela, si l'on tient toujours à ce que Pythagore soit le fondateur d'une nouvelle religion, il serait tout de même honnête de préciser, à un moment ou un autre, que cette nouvelle religion s'appelle la science.

 

La décision sur le serment est donc déterminante. Je dis bien la décision, car, est il authentique?  Le fait qu'il soit mentionné par 4 ou 5 auteurs est-il une preuve suffisante? Certainement pas. Si l’on nous dit que la lecture d'une trentaine de thèses, de préférence rédigées en allemand, peut aider à trancher la question, je ne suis pas sûr que ces arguments puissent bouleverser un épistémologue un peu cuirassé. Alors d'où pourrait provenir une preuve plus sûre? En fait, uniquement de l'archéologie, de la découverte d'une tablette où serait inscrite le serment, et qui serait datée grâce au carbone 14 de l'époque de Pythagore, où peu après. A force de confondre ses objectifs avec ceux de je ne sais quelle méthodologie (comme si les méthodes pouvaient donner des idées à ceux qui n'en ont pas) l'histoire se trouve de plus en plus réduite à attendre de l'archéologie ses possibilités d'orientation ou de décision les plus importantes.

La décision sur le serment est cruciale, parce que de cette décision dépend immédiatement l'interprétation totale de la doctrine. Autrement dit, dans les cas réellement décisifs : ce n'est pas "une garantie sur l'authenticité des sources" qui permet de se former "une idée sur la doctrine"; mais c'est au contraire l'idée qu'on s'est formée sur la doctrine, qui conditionne notre opinion sur l'authenticité des sources.

L'essentiel étant, dès lors, d'avoir au départ une certaine idée des choses, je ne vois pas comment la personnalité de l'historien pourrait n'être pas, la plupart du temps, le facteur décisif. Or à cet égard, il y a certaines "vocations universitaires" qui laissent un peu perplexe. Maurice Caveing, quels que soient ses mérites et l'utilité spéciale de son travail, est un idéologue positiviste comme Auguste Comte n'a sans doute jamais rêvé d'en voir naître. Il nous présente l'histoire des sciences comme une somme de petits progrès cumulatifs, modestes et laborieux. Quelle place pourrait bien trouver Pythagore dans un processus de lecture aussi écrasant? Si on lit sa thèse, qu'apprend-on du pythagorisme? On se demande surtout, en le lisant, comment l'idée a pu lui venir  de s'orienter vers l'étude de mentalités si étrangères à sa façon naturelle de penser. Et que dire de Festugière, longtemps autorité dominante en matière d'hermétisme, qui commence aujourd'hui à nous apparaître, avec le recul, et malgré sa croix, comme une incarnation presque fanatique, caricaturale, de la mentalité scientiste du début du XXe siècle?

*

  

Si Pythagore n’a ni écrit, ni même laissé de trace probante de sa pensée, c‘est au moins une hypothèse admissible, que ce fut de façon consciente et volontaire. Dans l’attachement à une forme exclusivement orale de la tradition, il pouvait y avoir une dimension réellement orgueilleuse : peut-être estimait-il qu’une doctrine qui ne réussirait pas à se conserver dans les cœurs, ne méritait pas qu'on s'en souvienne. Dans ce cas, ce ne serait pas par accident, mais par essence, par vocation même, que cette doctrine se refuserait à être saisie, ou cernée, par le critère ontologique de la trace, de la preuve matérielle et écrite, qui gouverne la science historique actuelle. Cela peut aussi être un début de réponse à une question que beaucoup se posent, savoir : Où se situe la coupure entre une éventuelle forme originellement pure et cohérente de la pensée pythagoricienne, et les formes lacunaires ou dégradées dont témoignent la plupart de nos sources. Etant donné, peut-être, le caractère déjà obsolète de la forme orale de transmission que Pythagore entendait maintenir, cette "écriture dans les coeurs" pourrait bien s'être avérée plus volatile qu'il le pensait; de sorte que la "décadence" pourrait avoir commencé dès l'extinction de Pythagore.

*

  

Il me reste à compléter ces remarques par un dernier mot concernant la notion d'ésotérisme. Cette notion ne présente pas les mêmes inconvénients que les notions de religieux et de mystique, dans la mesure justement, où l'ésotérisme est un paradigme dans lequel différents plans d'expérience ou de connaissance, du plus profane au plus sacré, (ou encore : s'étageant de la science à la spiritualité), peuvent se superposer, sans se confondre. Pour cette raison même, la notion d'ésotérisme est la seule dans laquelle pourraient légitimement (et sans risque de mélange ou de confusion) s'effectuer certaines correspondances entre le plan de la science et celui de la spiritualité. Cela explique aussi, incidemment, que je rencontre souvent moins de problèmes avec le Pythagore des ésotéristes, maçons et autres guénoniens, (bien que mon travail n'entretienne avec les leurs aucun rapport particulier), que je n'en ai, malheureusement, avec le Pythagore de certains historiens, qui à force de "suspension" et de "retrait" méthodologique, et corrélativement, à force d'amaigrissement  progressif de tout contenu intellectuel un peu précis, aurait tendance, de plus en plus,  à ressembler à je ne sais quel homme des cavernes, qui aurait découvert la multiplication par hasard en jouant avec des noix. Dans la démarche de certains historiens, il y a le rêve d’une position neutre, en quelque sorte sécurisée, qui serait une espèce de « distance parfaite » de la pensée. Mais en épistémologie, on apprend qu’il n’y a pas d’acte scientifique neutre. La suspension elle-même n’implique pas l’absence de thèse, puisqu’elle revient souvent, en pratique, à hypostasier des thèses fantômes, - des thèses qui, même lorsqu’elles ne sont pas énoncées, peuvent n’être pas moins décisionnelles et contraignantes que celles, par exemple, qui m’ont servi dans mon travail. Dans le cas de Pythagore, ces thèses fantômes peuvent être les suivantes : « Aucun des concepts hérités de la tradition pythagoricienne n’a de valeur centrale ou décisive pour l’interprétation totale de la doctrine. » Ou encore : « Si parmi les concepts hérités de la tradition, certains peuvent avoir une valeur centrale ou décisive, nous sommes incapables de dire lesquels. » Et derrière ces thèses qui ont encore un air assez précautionneux, s’en profile une autre, plus massive et en réalité seule déterminante, qui est que la doctrine de Pythagore n’a pas de consistance scientifique interne, qui en permettrait l’exposé par une méthode strictement hypothético-déductive.⁽²⁾

 

Août 2012

 

 

⁽¹⁾Dans le même courrier, Jean-Luc Périllié précise ainsi l'angle d'attaque : "l'intuition originaire qui avait gouverné mon travail résidait moins dans la philosophie du nombre proprement dite que dans l'étude de la filiation orphisme, pythagorisme, platonisme (que je considère comme relevant d'un déploiement "dynamique" dans un sens bergsonien)."

⁽²⁾La doctrine pythagoricienne relevant de la connaissance a priori, elle peut, par hypothèse, être reconstituée en totalité à partir de ses seuls principes, en n'importe quel point de l'espace ou du temps. Les questions de "copyright" qui font le souci permanent des historiens modernes, sur le fait de savoir si X a découvert cela tout seul, ou s'il l'a lu dans Y, qui lui-même le tenait de Z, (et dont le caractère obsessionnel ne traduit souvent rien de plus profond, qu'une adhésion un peu béate à l'idéologie de l'originalité personnelle et de la créativité "ex nihilo" de l'artiste moderne), si elles peuvent avoir un intérêt dans l'ordre de réalité qui est le leur, n'en ont réellement aucun au point de vue doctrinal, qui seul nous a importé dans ces études.

 

 

Références :

Peter Kingsley : Empédocle et la tradition pythagoricienne, Les Belles Lettres, 2010.

Jean-Luc Périllié : Symmetria et rationalité harmonique, origine pythagoricienne de la notion grecque de symétrie, L'Harmattan, 2008.

 

 

 

 

 

 

 

 

LA THEORIE GENERALE DU SIGNE

 

 

par Guillaume Denom

 

 

 à Antoine Abrassart

"The True" Scorpio Rising

 

 

 

Avertissement.

Le champ d'étude désigné dans cet article sous le nom de "théorie du signe" se distingue par deux traits essentiels. 1. Il envisage le signe en tant que réalité non seulement physique, mais véritablement matérielle. 2. Il présuppose que la mathématique est le champ approprié pour décrire la réalité définie en 1 sous le nom de signe. Ces deux traits, dans leur "restrictivité" même, empêchaient, comme on le comprend, d'utiliser les termes "sémiologie" ou "sémiotique", déjà associés à d'autres genres de réflexion sur le signe, ainsi qu'à d'autres définitions de ce concept.

 

 

 

Le tenseur binaire radical

 

Lorsqu'on la représente par la lettre V, la dyade indéterminée apparaît morphologiquement analogue au tenseur binaire radical de la linguistique guillaumienne, concept que cette théorie définit comme "l'opérateur universel de la structure du langage". La linguistique guillaumienne se distingue des autres écoles linguistiques par sa visée synthétique. Ce qui l'intéresse n'est pas, prioritairement, l'analyse architectonique du "système de la langue", mais un fait linguistique plus profond, agissant à chacun des niveaux de ce système, que son auteur qualifie de "psychomécanisme", ou, ailleurs, de "mécanisme de puissance de la pensée humaine". Il s'agit donc d'un opérateur antérieur à la problématique propre du langage et du signe, puisqu'il se rapporte, plus originairement, à la parole, en tant que geste et action entière de l'homme, non encore décomposée. Citons Gustave Guillaume :

"La pensée tient sa puissance de ce qu'elle est habile à particulariser et à généraliser. Privée de cette double aptitude - qui constitue un entier (un entier intérieurement binaire) - la pensée serait sans force et inopérante. Or, si de ces deux opérations - particularisation et généralisation - desquelles la pensée tient sa puissance, on ne retient abstractivement que ce qu'elles comportent de mécanique, elles se réduisent à deux mouvements de pensée, l'un allant du large à l'étroit, (inhérent à la particularisation), l'autre allant de l'étroit au large (inhérent à la généralisation). Une réduction abstractive infléchie selon la pente arithmétique ramènerait la particularisation à un mouvement allant du plus au moins, et la généralisation à un mouvement allant du moins au plus. Le mécanisme de puissance de la pensée, c'est l'addition sans récurrence, sans retour en arrière, de deux tensions, une tension I fermante progressant du large à l'étroit, et une tension II ouvrante progressant de l'étroit au large, soit figurativement :  

 

 

A ce mécanisme de puissance, on a, dans cet ouvrage, donné le nom pleinement justifié de tenseur binaire radical."

L'analogie entre ces deux notions : dyade indéterminée, et tenseur binaire radical, n'est en rien superficielle, mais, au contraire, tout ce qu'il y a de plus profonde; puisque ces deux notions constituent les fondements opposés, mais complémentaires, d'une discipline bipartite qui est la théorie générale du signe. Plus précisément, nous verrons que le tenseur binaire radical est à la théorie du signe linguistique, ce que la dyade indéterminée est à la théorie du signe mathématique, catégorie qui intègre, ici, une variété de systèmes de signes, tels que les systèmes d'orientation, les gammes musicales, ou les calendriers, dont la nature mathématique est comparable à celle des objets les plus fondamentaux produits par cette science, - tels que les nombres et les figures -, et dont le "substrat" ou le cadre transcendantal est le même, puisqu'il est celui des catégories universelles de l'espace et du temps. Et l'on s'apercevra qu'entre ces deux domaines ou ces deux visages du signe, le signe mathématique et le signe linguistique, la frontière, même si elle existe, n'est pas aussi épaisse - ni étanche - qu'on pourrait le penser de prime abord.

 

*

 

La théorie générale du signe est un point de vue depuis lequel on considère les systèmes de signes, ou encore, les paradigmes¹, tels que, pour s'en tenir à un niveau élémentaire, les alphabets et les gammes musicales, comme formant eux-mêmes de "gros" signes unitaires et organiques, comme de pures singularités morphologiques. Dans cette théorie, on s'efforce d'appréhender d'un point de vue extérieur et équidistant, d'un côté, le nombre, à savoir, en l'espèce, des systèmes de signes, tels que les gammes musicales, qui sont issus de l'intuition d'une quantité mathématique discrète, et qui reposent donc sur un fondement stable et éternel, "a priori", sur un rapport intuitif et immédiat au même, à l'identité du nombre; et de l'autre, le verbe, ou le signe linguistique, dans toute sa naturalité, sa contingence initiale, son "instant d'arbitraire", qui fait qu'aucun nom, d'aucune langue, ne sait nommer les choses exactement dans la même "guise" qu'un autre. Or le tenseur binaire radical, dont l'ambition est de réduire le processus de la signification à un mécanisme universel, a précisément aussi la charge d'expliquer la genèse concrète, matérielle, du signe linguistique; et cet opérateur semble bien recéler cette capacité insigne, de savoir exhiber à la fois l'universalité, la constance, l'unicité du geste linguistique, et sa parfaite contingence ou déterminité naturelle, puisqu'il se distingue par ses applications spectaculaires à des faits de langue précis et localisés, tels que, par exemple, le système de l'article français, ou celui de la flexion nominale. 

 

 

Le système phonologique des consonnes du français

 

Le tenseur binaire radical est efficient, pour commencer, dès le premier degré de la morphogenèse du langage, celui de la constitution du système phonologique, qui s'effectue par la transformation du continuum acoustico-vocalique de la phonation, en un champ d'unités discrètes : les phonèmes. Les tensions 1 et 2, "fermante" et "ouvrante", y jouent alors, très précisément, le rôle que jouent, dans le système morphogénétique de Turing, les fonctions chimiques, ou morphogènes, "inhibiteur" et "activateur", dont on sait qu'elles engendrent, en phases d'équilibre, des réseaux de gros points distribués en symétrie hexagonale; ce qui explique, comme nous allons tenter d'en exposer brièvement la raison profonde, l'omniprésence des structures hexagonales et des relations logiques biternaires dans la plupart des systèmes phonologiques.

  

structures de Turing, avec à gauche, phase d'équilibre hexagonal

  

La structure phonologique la plus caractéristique est une structure de type "sceau de Salomon", dans laquelle une relation ternaire faible, ou secondaire, est posée en tempérance d'une relation binaire forte, ou première. Sur un plan purement logique, la première différence constructive d'un système est, par définition, toujours binaire, mais il faut bien comprendre que le binaire est, fondamentalement, l'opérateur le plus impropre à la construction du continuum; ce que l'on peut illustrer sur le plan de la logique première, en remarquant que le segment, parce qu'il est la première différenciation de la monade, est aussi l'objet monadique qui ressemble le moins au point; et en effet les objets monadiques de rang 3 et 4, le disque et la boule, ressemblent plus au point que le segment. La relation ternaire joue donc le rôle de tempérance maximale de la relation binaire, - ou si l'on veut, de médiété - tempérance qui permet à une relation d'opposition binaire de se rapprocher le plus vite d'un envahissement général du continuum. Ainsi, dans le système phonologique des consonnes du français, les relations binaires fortes sont les relations "sourde/sonore" et "occlusive/fricative"; tandis que les relations ternaires se disposent en médiation (dentale/labiale/gutturale), ou en extension (nasale/liquide/semi-voyelle) de ces relations binaires fortes.

 

  

(Remarques.

I. Par souci de simplicité, les phonèmes sont ici désignés biunivoquement par des lettres de l'alphabet, qui, comme on le sait, sont souvent plurifonctionnelles. Pour être correctement interprétées, les lettres doivent être ici oralisées dans le paradigme "a";⁽¹⁾ c'est-à-dire que, pour connaître la valeur exacte des phonèmes du tableau ci-dessus, il suffit de faire suivre les lettres qui les désignent par la lettre "a"; ainsi, pour préciser les cas litigieux : "carte" et "garde" pour les occlusives "c" et "g", "wapiti" et "yak" pour les semi-voyelles "w" et "y", "chat" et "sable" pour les phonèmes "ch" et "s", "zazie" pour "z", etc.)

II. Contrairement à l'opinion de divers linguistes, aucun phonème du troisième niveau n'est inclus dans la classe "sonore". Même si nous avons pu constater que certains linguistes demeuraient réticents au principe autoritaire de la logique, la catégorie "ni sourde ni sonore" constitue pour nous une catégorie indispensable du système, pour une raison simple, qui est que la relation sourde/sonore constitue un ensemble biunivoque parfaitement compact. En effet, une sourde se transforme univoquement en la sonore correspondante par "sonorisation"; et réciproquement, cette sonore se retransforme univoquement en la sourde de départ par "assourdissement". La classe "ni sourde ni sonore" désignant dès lors, ni plus ni moins, l'ensemble des phonèmes qui sont exclus de cet ensemble biunivoque clos et complet. La catégorie phonologique "voisé - non voisé", qui implique une redistribution des trois classes : sourdes, sonores, ni... ni..., en deux classes seulement, n'a donc en français qu'une valeur descriptive, mais elle n'est pas pertinente pour l'analyse du système.

III. Ce tableau constitue, bien évidemment, un système complet des consonnes du français, définies selon la méthode jakobsonienne de permutation de la syllabe. Il recense donc l'ensemble fermé des 18 solutions "c" existant, en français, pour remplir une matrice de syllabe à deux éléments simples  (c : Consonne / v : Voyelle).

Soit de ligne en ligne :

- table (T), partie (P), carte (C), sable (S), fable (F), chat (cH), pour les sourdes;

- dame (D), bac (B), gare (G), Zadig (Z), valise (V), jaloux (J), pour les sonores;

- navet (N), mare (M), rat (R), lac (L), wapiti (W), yak (Y), pour les ni sourdes ni sonores. 

La lettre X, comme on le sait, ne correspond pas à un phonème, mais à 4 phonèmes différents, les deux sourdes de Félix (CS) et les deux sonores de Xavier (GZ); cette lettre signalant donc, par sa fonction comme par sa forme, le centre géométrique du paradigme sourd/sonore. La lettre K est un substitut phonologique de C. Enfin la consonne manquante de l'alphabet français, la fricative "ch" de "chat", est ici "représentée" par le graphème "inutile", non phonologique, de ce même alphabet : la lettre H; car, comme l'a indiqué Saussure, on ne peut en aucune manière appeler "phonème" un signe qui n'a d'autre existence phonétique, que le fait qu'on ne puisse faire, devant lui, ni liaison ni élision.

IV. Voyelles. Il n'existe pas de système constant des voyelles du français. Leur dénombrement même est impossible, étant sujet à des variations locales. Ainsi, les voyelles finales des mots "chacun" et "demain" correspondent à des phonèmes identiques à Paris, mais distincts à Toulouse. Pour les voyelles des mots "chauve" et "porte", c'est l'inverse : elles correspondent à des phonèmes identiques à Toulouse, mais distincts à Paris. Le français apparaît donc, à cet égard, moins différent qu'on pourrait le penser des langues sémitiques, dans lesquelles les voyelles sont réputées n'avoir pas d'existence véritablement individuelle. En revanche, le système des consonnes est rigoureusement constant, quelles que soient les différences d'accent ou de réalisation locales. Le phonème "r" peut-être roulé ou non selon les régions, il reste fonctionnellement un "r", c'est à dire qu'il conserve partout la même fonction dans le système.)

  

Si maintenant toutes ces relations biternaires sont déployées, ou libérées, non plus dans le champ logique bidimensionnel qui est celui d'un tableau analytique, mais dans un espace de diffusion "théorique" tridimensionnel, on s'aperçoit qu'elles se solidifient spontanément en un prisme hexagonal. Pour passer d'une structure à l'autre, il suffit d'enrouler le plan du tableau ci-dessus, en mettant bout à bout ses côtés gauche et droit.

 

  

Ce que l'on pourrait commenter ainsi : les relations logiques biternaires de type "sceau de Salomon" constituent l'opérateur de différenciation le plus rapide et le plus efficace pour transformer un "segment" (c'est-à-dire une relation d'opposition binaire) en un "disque" (hexagone), puis en un "cylindre" (prisme); ou encore, pour permettre à cette relation d'opposition d'envahir l'espace à trois dimensions.⁽²⁾

Pour que le modèle mécanique guillaumien soit opérant, il faut donc considérer que la tension 2, la tension ouvrante, est la tension binaire, ou "paire", tandis que la tension 1, la tension fermante, est la tension ternaire, ou "impaire". En effet, le ternaire étant toujours polarisé par un centre de symétrie qui est structurellement son origine, (centre correspondant ici aux catégories "labiale" d'une part, et "liquide" d'autre part) une tension ternaire peut être "fermante", ou "inhibitrice", lorsqu'elle est, géométriquement, une tension de contraction du segment (2) vers le point qui est son centre (1); ou bien, si l'on raisonne sur un triangle, une tension de contraction de ce triangle, régressant géométriquement de l'un de ses côtés (2), vers le sommet opposé (1).

 

 

La structure complète du système des consonnes pouvant dès lors se déployer en trois coups de temps seulement, trois entiers guillaumiens, ou trois "guillaume" correspondants aux trois étages de la structure ci-dessus; car nous attachons pour notre part le plus grand prix à cette propriété du tenseur binaire radical, un peu négligée par les guillaumiens et peut-être par G. G. lui-même, de permettre une expression quantifiée, et en ce sens véritablement scientifique, de la différence énergético-informationnelle dans laquelle consiste ultimement le signe. Notons que ce modèle apparaît en tout point conforme au formalisme logique de la dyade indéterminée, dans lequel l'impair, le fermé, précède toujours le pair, l'ouvert.

 

Notons que l'ensemble du système peut, à son tour, faire l'objet d'une résolution ternaire "fermante", ou "inhibitrice", analogue à celles qui opèrent à chacun de ses étages (au prix de l'ajout, dans le décompte des temps du système, d'un temps de genèse supplémentaire, logiquement antérieur aux trois moments dénombrés ci-dessus, et qui correspond, comme on le verra plus loin, au moment "zéro" de la théorie pythagoricienne du signe, qui est celui de la coordination du système avec lui-même); à cette réserve près que, dans une telle application, c'est l'étage inférieur, le "ni-ni", qui devrait plutôt occuper la position centrale, et donc le niveau médian de la structure, puisque ce connecteur logique correspond bien réellement, ici, au pôle de l'imparité et de la fermeture, qui, selon le formalisme de la dyade indéterminée, s'oppose à la parité et à l'ouvert de l'ensemble biunivoque "sourdes et sonores".⁽³⁾ Précisons que la disposition adoptée dans les figures ci-dessus résulte uniquement de la contrainte bidimensionnelle de la logique de tableau (logonique), adoptée ici par simple commodité et en raison de sa richesse analytique. Mais la représentation suggérée dans le présent paragraphe apparaît préférable d'un point de vue synthétique, en ce qu'elle permet d'exprimer le système, non plus sous la forme du quasi-cylindre (prisme), mais sous celle du sphéroïde ou de la quasi-boule topologique, en assignant à l'ensemble hexagonal "ni-ni" la fonction topologique d'un disque équatorial, et aux ensembles "sourdes" et "sonores" celle, logiquement seconde, de disques tropicaux, respectivement nord et sud. Or la représentation sphérique, en raison de sa nature monadique, correspond, comme on le verra plus loin, à l'expression mathématique optimale du processus d'envahissement constructif du continuum perceptif, dans lequel consiste toute la nature du signe linguistique matériel.

 

 

 

*

 

Le choix, par Gustave Guillaume, d'un modèle mécanique, plutôt qu'un modèle chimique ou autre, est, à lui seul, assez lourd de conséquence. Il peut se réclamer d'un certain principe d'économie scientifique, qui est celui du "moindre besoin". La science trouve toujours meilleur ce qui est fait avec des moyens plus "rustiques", lorsque ceux-ci s'avèrent suffisants. Mais surtout, le choix d'un modèle mécanique a pour effet de placer, par hypothèse, l'organe du langage - ou si l'on veut, son centre organisateur - beaucoup plus près du corps et de son activité mécanique, sinon musculaire, que du cerveau, et de son activité chimique ou électrique.

 

*

Ces deux notions, dyade indéterminée et tenseur binaire radical, nous représentent donc les deux visages, ou les deux côtés du signe; un côté qui implique, originairement, passivité, prudence, patience ou réceptivité, (la tétractys, par exemple, est essentiellement un "récipient", ou un "réceptacle", pour reprendre la terminologie technique du Timée), et qui est tourné vers ce qui est stable, constant, et éternellement le même, vers le nombre; et un autre côté qui consiste, originairement, en une action, en un engagement en quelque sorte libre, souverain, ou créateur, dans la matière, avec tout ce que cela comporte de "hasard heureux" et de "chatoiement" poétique de l'être, et qui est la parole, en tant que geste et action générique de l'homme. La connaissance pythagoricienne n'étant qu'un accord, ou une harmonie, entre cette naturalité et cette éternité. Car ces deux côtés du signe ne peuvent jamais, en effet, être séparés complètement l'un de l'autre, puisque même le nombre, pour être reçu, doit d'abord être saisi par l'entremise d'un nom. Inversement, on a vu, avec Gustave Guillaume, que l'opérateur le plus profond de la langue se réduisait, en définitive, à un infléchissement arithmétique, à une espèce de tendance à "imiter" le nombre.

 

  

Systèmes d'orientation, gammes et calendriers

 

A la famille des systèmes "mathématiques" appartiennent, outre les gammes musicales, les systèmes relevant du paramétrage de l'espace temps, tels que les systèmes d'orientation et les calendriers. Les problèmes de "comma" musical sont, mathématiquement, analogues à ceux posés par le comput calendaire. La tendance à une stabilisation hexagonale ou dodécagonale - en considérant que ces diverses divisions du temps peuvent être représentées par des divisions du cercle - demeure, néanmoins, assez générale à ces systèmes (gammes et calendriers). Le système babylonien, conservé par la civilisation moderne, est sexagésimal; l'année, comme le zodiaque, comme la journée, et comme l'heure de nos horloges, a 12 divisions; et notre système musical, après une computation interne de plus de deux mille ans, s'est stabilisé en une gamme tempérée de 12 demi-tons, soit 6 tons entiers.

  

 

Les couleurs

 

D'autres systèmes, enfin, appartiennent à une catégorie intermédiaire; ainsi, les systèmes de noms de couleurs internes à chaque langue naturelle qui, bien qu'ils relèvent de la contingence linguistique, réalisent, la plupart du temps, un paramétrage mathématique à peu près idéal, et quasi constant, du spectre de la couleur. Les mêmes "stations" se rencontrent, à quelques nuances près, dans la plupart des idiomes occidentaux, permettant une transmission relativement aisée, d'une langue à l'autre, de l'expérience de la couleur, pourtant incommunicable par nature, en l'absence d'un référent universel et non subjectif. "Les couleurs", en effet, n'existent pas, puisque la couleur est originairement un phénomène singulier, un continuum. Le bleu n'est, en soi, rien de plus que la somme des expériences et des idées humaines qui se sont accrochées au mot "bleu", depuis que ce mot est utilisé (comme le démontre suffisamment, par exemple, le fait qu'il corresponde à deux mots différents en langue russe). Le référent des couleurs que nous avons l'habitude de nommer comme des individus, n'a donc, en toute rigueur, aucune existence absolue en dehors des noms naturels qui en fixent la notion. Son concept ne se "substantialise" que par un va et vient à la vérité fort subtil, dans lequel entrent en jeu, simultanément : 1) la consistance topologique intrinsèque, originairement locale, du seul système de signes - le système des noms de couleurs - qui, par sa vertu propre d'opérateur de différenciation, détermine ces signes, dans leur usage, tantôt à s'attirer, tantôt à se fuir magnétiquement de proche en proche, par un mouvement devant normalement les conduire, dans leur devenir utilitaire, à se satelliser, (sur le continuum virtuel dont ces unités transportent le principe avec elles), à une distance étalon de valeur 1 les uns des autres; et 2) la confrontation permanente de ce même système avec l'expérience quotidienne, qui amène la notion de ces signes à "s'infuser" graduellement de réalité ou de substantialité empirique, par un  mouvement de reconnaissance par "approches" - ou par une "approximation" perceptive;⁽⁴⁾ - ces deux mouvements, pour finir, se soutenant et se guidant l'un l'autre. Dans la genèse concrète du système, on peut imaginer que ce dynamisme, ce mouvement "optimiste" de la signification, puisse commencer à s'activer à partir d'un graphe rudimentaire de, par exemple, 4 ou 5 unités, dont la structure ou la configuration définitive demeurerait, dans un premier  temps, indécise, ou fluctuante; c'est à dire que l'on peut imaginer une langue primitive qui ne disposerait que de quatre ou cinq noms de couleurs. En revanche, nos systèmes modernes relèvent probablement d'un lent processus de "décantation" statistique, ou économique, de nature essentiellement pratique.

 

 

 

Structure "sablier" du paradigme français des noms de couleurs

 

 

Triangle "Mondrian".

Couleurs dites "primaires" (Rouge-Jaune-Bleu)

 

 

Triangle "Malévitch".

Couleurs dites "alchimiques" (Rouge-Noir-Blanc)

 

 

Chacun des "registres" du sablier enferme virtuellement une structure hexagonale biternaire de type "sceau de Salomon". En outre, la structure générale du sablier lui-même est topologiquement analogue à la structure "fermante-ouvrante" du tenseur binaire radical; de sorte que le système peut nous apparaître comme formant un "super-entier" guillaumien fermant-ouvrant,  composé en réalité de deux entiers conjoints ou "siamois".

 

Ce paradigme linguistique est, par exemple, rigoureusement identique à celui de la langue anglaise, où les onze stations du sablier (brown, black, grey, white, pink, red, orange, yellow, green, blue, purple) correspondent, comme en français, aux onze noms de couleurs qui sont statistiquement les plus utilisés. De tels paradigmes peuvent être qualifiés d'"optimaux", en ce qu'ils réalisent un compromis parfait entre une variété de contraintes empiriques, voire expérimentales, dont les unes sont optiques, telles que le paramétrage des "couleurs de l'arc-en-ciel", ou, plus exactement, de l'expérience visuelle de la décomposition de la lumière (triangle supérieur), et les autres physico-chimiques, telles que la fabrication de nuances "intermédiaires", par le mélange de matières, ou de pigments colorés "primaires" ou fondamentaux (ensemble du paradigme). 

 

La même structure peut être déployée sur un axe continu, par exemple un escalier, sur lequel les stations fortes arrivent une fois sur deux. Ainsi, si l'on part du noir, les 5 stations fondamentales sont les stations impaires.

 

 

 

En conclusion de cet aperçu sur la couleur, on peut remarquer que la relative impuissance des théories modernes de la couleur à cerner la véritable essence de cette dernière, résulte assez généralement de la conviction partagée (bien antérieure à la notion officielle - d'ailleurs falsifiée et infidèle à la véritable pensée de Saussure - d'arbitraire "pseudo-saussurien" du signe), que la couleur ne peut de toutes façons pas résider dans son nom, pour la raison que celui-ci ne peut être qu'un signe "arbitraire" ou "conventionnel", au sens assez banalement négatif et réducteur que peuvent revêtir ces deux expressions. Ce préjugé assez général a conduit les théoriciens modernes à chercher, tantôt à objectiver la couleur par quelque procédure expérimentale chimique ou optique, tantôt, à l'exemple de Goethe ⁽⁵⁾, à la résorber dans le registre subjectif de la pure sensibilité, sinon même de l'émotivité. Mais ce qui a échappé à tous, (y compris au pourtant très sagace Newton) c'est qu'une fois qu'on avait produit toutes ces "simulations" phénoménologiques de la couleur, on avait seulement montré les raisons de la couleur, ses motivations en quelque sorte externes et contingentes - mais toujours pas la couleur elle-même, dont le contenu possible était pourtant "connu" et déterminé depuis le début, puisqu'il résultait de la toute puissance productive, a priorique et en quelque manière magnétique, émanée de la seule hypostase originelle de son nom.

 

  

De la consistance logique continue de la théorie du signe matériel, à travers la nature mathématique diverse de ses principaux continuums de référence

 

Un témoin significatif des conceptions qui étaient celles des pythagoriciens, en matière de théorie du signe, est ce fameux passage du Protreptique d'Aristote, où l'on compare les trois doubles consonnes grecques formées à partir de la lettre sigma, avec les trois accords fondamentaux de l'harmonie musicale, rapportés à l'unisson. Cette comparaison à laquelle le malheureux Aristote ne comprend goutte, parce qu'il ne saisit pas le point de vue depuis lequel elle est énoncée, est d'une profonde pertinence théorique, comme on peut tenter, ici même, de l'exposer en quelques traits; et elle n'est pas le seul témoin du haut degré de technicité et de rigueur formelle qu'avaient acquis les spéculations des pythagoriciens, en matière de théorie du signe.

Mais avant d'entrer dans le coeur du problème, il convient d'évoquer certaines considérations générales concernant la théorie du signe, qui ne pouvaient être abordées avant que des exemples précis du genre de systèmes auquel cette théorie s'applique, fussent produits, ou extensivement définis.

En tout premier lieu, il convient de se défaire de l'idée que puisse exister, dans la théorie du signe, un plan phénoménologique correspondant à celui de la pure sensation, ou d'une réception sensorielle absolument passive, dénuée de toute intentionnalité, de toute dimension active, telle qu'en subsument, le plus souvent, les catégories rigides de la psychologie moderne, quelques diverses qu'elles puissent être.

Les différents continuums sur lesquels raisonne la théorie du signe matériel, ne sont pas à proprement parler des continuums sensoriels, mais bien plutôt perceptifs, c'est à dire qu'ils comportent tous un élément relevant d'une certaine "magnétisation" préalable, ou "intentionnelle" et par conséquent active de la sensibilité, transcendante à l'indéterminité purement "objective" du fait sensoriel. Cependant, ces continuums se distinguent entre eux par le fait de comporter, les uns par rapport aux autres, une plus ou moins forte proportion de réceptivité, de passivité, ou au contraire d'opérativité et d'activité.

De la même manière, le point commun aux différents systèmes que l'on a envisagés ici, est de consister, chaque fois, en une action organique de structuration d'un certain continuum perceptif, par la constitution d'un système d'unités discrètes régi par des interrelations logiques (elles-mêmes assimilables à autant de "logoi", ou de rapports d'entiers pythagoriciens); cependant, ces continuums ne comportent pas nécessairement le même nombre de dimensions mathématiques "théoriques", comme on peut aisément s'en rendre compte à l'usage. En effet.

Le continuum de la tonalité, abstraction faite de ses conditions de réalisation pratiques, peut être représenté par un axe mono-dimensionnel (dimension pythagoricienne 2),⁽⁶⁾ comme il l'est dans la représentation courante du langage, où il est symbolisé par un axe appelé tantôt "haut-bas", tantôt "aigü-grave", expressions qui ont des sens assez voisins. Le continuum de la couleur, avec l'expression de ses différences combinatoires biternaires de type "sablier", requiert, quant à lui, au moins deux dimensions (dimension pythagoricienne 3); c'est-à-dire que, même si l'expérience de la couleur pourrait, en théorie pure, être communiquée à un sujet ne connaissant que l'existence de deux dimensions, elle nécessite au minimum cette capacité de percevoir un "écran", sur lequel puissent apparaître différentes "taches colorées". Enfin le continuum de la phonation se distingue à son tour de ces deux premiers exemples, en ce que sa définition ne procède pas d'une seule aire sensorielle (telle que l'"oreille" pour la musique, ou l'"oeil" pour la couleur, dans une acception anatomique volontairement vague de ces deux "organes" sensoriels) mais de l'interconnexion de deux aires sensorielles; car en effet, le continuum de la phonation n'est pas seulement vocalique, mais acoustico-vocalique, de sorte que, bien qu'il soit entièrement immergé dans le domaine de l'empirique et du perceptif, il résulte de la mise en correspondance de deux "aires" sensorielles antagonistes, l'une active, représentée par l'appareil phonatoire, l'autre passive, représentée par l'organe de réception des sons élaborés par ce dernier. C'est pourquoi les propriétés d'un système tels que celui des consonnes, ne peuvent complètement se déployer que dans une dimension théorique supérieure à celle du plan, par conséquent en dimension pythagoricienne 4.

Le continuum de la tonalité peut apparaître, à cet égard, comme le plus passif, en ce qu'il est indépendant des conditions concrètes de sa production, que celles-ci puissent être actives ou non n'ayant aucune incidence en la circonstance. La musique est en effet la réception d'un rapport arithmétique absolument pur et constant, dont la saisie ne nécessite aucun "geste" ni "exercice" musical particuliers, pas plus qu'elle n'exige la connaissance consciente des valeurs numériques correspondantes aux accords musicaux, puisqu'elle relève d'un registre empirique plus profond que ceux-là, que l'on peut légitimement qualifier de "subconscient" ou, si on préfère, de supra-conscient, qui est celui, tout naïf ou naturel, du sentiment immédiat de l'accord ou de l'harmonie, du "juste" et du "faux".

A l'inverse, le continuum acoustico-vocalique de la phonation est dépendant de la coordination préalable d'un appareil de production, avec un plan de réception antagoniste; et de ce fait, il intègre une plus forte proportion d'opérativité, d'activité, voire de "gestualité", dans sa constitution matérielle même, que le continuum tonal.

Ces divers points précisés, il paraît maintenant plus aisé de gloser le fragment pythagoricien du Protreptique d'Aristote.

La saisie pythagoricienne considère les trois doubles consonnes grecques formées à partir de la lettre sigma comme constituant hypothétiquement l'axe vertical polaire du système des consonnes; en considérant comme point zéro ou origine polaire de ce système, la lettre sigma elle-même en tant qu'elle n'est coordonnée à aucune autre. Puis il établit une correspondance entre ces trois modes de coordination de la lettre sigma, et ces trois rapports de coordination de la note tonique que sont respectivement la quarte, la quinte et l'octave. Soit :

 

0. Sigma - Ton

1. Ksi  - Quarte

2. Psi - Quinte

3. Dzêta - Octave

 

On peut remarquer que les trois niveaux déployés ici correspondent, en grec comme en français, au ternaire fondamental des points d'articulation de la phonation : guttural - labial - dental; de sorte que le "retour" de la dentale originaire (sigma) dans le dernier rapport (la lettre dzêta étant une combinaison de deux dentales) se trouve correspondre, terme à terme, au retour cyclique, ou "hélicoïdal", de la position de l'origine (ton) dans le rapport d'octave. On peut ensuite remarquer qu'en français aussi, l'axe polaire du système des consonnes coïncide avec celui qui traverse les doubles consonnes formées à partir de la lettre S : savoir la double-sourde de Félix et la double-sonore de Xavier, même si le français ne possède pas d'autres doubles consonnes naturalisées dans l'alphabet, et si dans le système propre à cette langue, le ternaire le plus fondamental est un ternaire différent de celui des points d'articulation.

N'en déplaise à Aristote, une telle comparaison apparaît donc bien légitime, si on la considère, avec la méthode adéquate, sous l'angle scientifique particulier qui est celui de la théorie du signe, domaine, il est vrai, dont cet auteur assez peu mathématicien, ne soupçonnait probablement pas même la possibilité de l'existence.

 

  

⁽¹⁾ En sympathie, pour une fois, avec les variations de l'usage moderne à ce sujet, le terme "paradigme" désigne, synthétiquement, dans nos pages, comme il le faisait, il me semble, dans la pensée des anciens, à la fois l'exemple, et le système de coordonnées, ou encore l'ensemble, non nécessairement clos, dont cet exemple est un exemple; la consistance de notre travail permettant, chaque fois, de savoir dans quel sens il est utilisé. Pour employer une image, le terme paradigme désigne la roue d'un système, en tant qu'elle peut être représentée par chacun de ses rayons, ou mieux encore, en tant que la nature même d'une roue ne consiste, ou ne résulte, que de la possibilité qu'ont ses rayons de permuter, de prendre la place l'un de l'autre

⁽²⁾ Pour être plus précis, la structure à trois étages du système phonologique des consonnes du français contient deux ensembles de structure biternaire, ou "sceau de Salomon" : l'ensemble "sourd" (t-p-c, s-f-ch) et l'ensemble "sonore" (d-b-g, z-v-j), et un ensemble de structure terbinaire, correspondant ici au rez-de-chaussée de la structure : l'ensemble "ni sourd ni sonore"  (n-m, r-l, w-y).

⁽³⁾ Dans notre article sur la construction pythagoricienne de la géométrie, en page 1 de ce blog, nous avons présenté le connecteur logique "et" (synthétique) comme un opérateur "entrant" ou "fermant", et son antagoniste, le connecteur "ni..., ni..." comme un opérateur "ouvrant". Pas de contradiction ici néanmoins. Le "et" dont il s'agit ici est bien le "et" analytique et ouvrant ("un homme et un chien se rendaient au marché"), auquel s'oppose, comme son complément, un "ni..., ni..." synthétique, et fermant, désignant un objet qui n'a aucune des deux propriétés en question, ou qui, à la rigueur, les possède "l'une et l'autre à la fois", sur le mode de l'indistinction. Pour des raisons naturelles, dont l'explication nous entraînerait trop loin, le système phonologique des consonnes utilise, précisément, les fonctions des connecteurs logiques au rebours de celles qui sont les leurs dans la logique prédicative.

⁽⁴⁾  Cette notion d'approche, ou d'approximation perceptive peut, à première vue, apparaître paradoxale; mais elle ne l'est que si l'on ne considère la perception que comme un fait absolument passif, calqué sur la rigidité du schéma psychologique moderne : émetteur - récepteur, ce qu'elle ne peut être en aucune manière dans l'ordre phénoménologique qui est celui de la couleur; puisqu'on peut poser en principe qu'un sujet n'a, a priori, aucune chance particulière de rencontrer dans son champ de perception du vert, du rose, de l'orange, s'il n'a, auparavant, activé en quelque manière le "tenseur" ou "l'attracteur" capable de motiver et de guider une semblable "rencontre", et dont le foyer ne consiste que dans l'idée abstraite de la couleur, dans son concept même.

⁽⁵⁾ Sachant que, comme l'a lucidement indiqué Wittgenstein, la "théorie des couleurs" de Goethe est un travail littéraire qui, quelle que soit sa valeur, ne contient aucune théorie scientifique de quelque nature que ce soit. En revanche sa querelle à l'encontre de Newton nous fait l'effet d'un chef d'oeuvre d'incompréhension, mais aussi de prévention imbécile contre ce qu'il s'imagine être "l'esprit mathématique"; préjugé d'autant plus regrettable de la part d'un auteur qui se voulait, avec sincérité sans doute, un philosophe de la nature.

⁽⁶⁾ Précisons que nous ne parlons là que du continuum tonal absolument pur et a priori, indépendamment des systèmes d'unités discrètes que l'on peut définir à l'intérieur de lui; car, une fois mathématiquement qualifié, l'axe monodimensionnel de ce continuum devra nécessairement adopter la forme de l'hélice (ou de l'"escalier hélicoïdal"), afin d'exprimer la récurrence périodique des rapports harmoniques qu'il contient.

 

 Décembre 2013

 

 

Référence :

Gustave Guillaume : Essai de mécanique intuitionnelle - t. 1,  Espace et temps en pensée commune et dans les structures de langue, Presses de l'université Laval, Québec, 2007.